5. РЕЛЯТИВИЗМ В НОВОЙ ФИЗИКЕ

5.1. Область релятивизма.

Частица, двигающаяся по винтовой траектории со скоростью V, не является релятивистским объектом, но ее компоненты всегда релятивистские объекты, поскольку двигаются по орбите этой частицы со скоростью света.

По известному выражению новой физики для электрона:

                                                   (5.1.1),

где  = 1,1576 см²/сек. Из (5.1.1) определим радиус винтовой траектории электрона, который движется со скоростью света:

1,1576/2,997924×10¹⁰=386,134×10^-13 см = 386,134 фм      (5.1.2).

Из (5.1.2) совершенно ясным становится физический смысл величины, которую официальная физика называет «комптоновская длина волны электрона»:

= 1,0545727×10^-27 / 9,109390×10^-28 × 2,997924×10¹⁰ = 386,1594 фм=r₀  (5.1.3).

Оказывается – это тот минимальный радиус винтовой траектории электрона, на котором он приобретает скорость света и становится релятивистским, т.е. вместо Vr=const, будет следовать mr=const для удовлетворения закона сохранения момента импульса.

Из (5.1.3) можно уточнить значение  = 1,1576765 см²/сек для электрона. Поскольку любые микрочастицы обладают одинаковым моментом импульса на винтовой траектории , то для них:

                                               (5.1.4),

поэтому для них минимальный нерелятивистский радиус винтовой траектории (комптоновская «длина волны» для данной частицы):

                                              (5.1.5).

Из (5.1.5) видно, что «длина волны» получится лишь при умножении обеих частей равенства на 2, при этом получим длину волны де Бройля для частицы, движущейся со скоростью света. Таким образом, официальная физика не понимает, что такое .

Официальная физика считает, что релятивизм начинается там, где энергия частицы становится больше «энергии покоя». Новая физика согласна с этим утверждением:

                                                 (5.1.6).

Знаменитое выражение (5.1.6) ничто иное, как сумма кинетической энергии частицы поступательного и тангенциального движения со скоростью света на винтовой траектории. Напомню читателю, что действительная скорость частицы, у которой поступательная скорость равна скорости света, составляет , но эту скорость, пока, невозможно экспериментально определить. Если учесть, что , то (5.1.6) перепишется в виде:

                                                   (5.1.7).

Из (5.1.7) видно, что при радиусе винтовой траектории меньше r_0i частица находится в релятивистской области, а радиус ее винтовой траектории обратно пропорционален энергии. Чтобы достичь нулевого радиуса, необходимо сообщить частице бесконечно большую энергию, масса такой частицы тоже будет бесконечно большой. В связи с этим можно предполагать, что с ростом мощности ускорителей частиц будут открывать все новые и новые частицы с возрастающими массами, поэтому на удовлетворение этого любопытства лучше не тратить деньги впустую, пока хватит существующих ускорителей и космических лучей.

Очевидно, что (5.1.6) не подходит для нерелятивистской области, т.к. дополнительная энергия расходуется на увеличение скорости, а не на увеличение массы частицы. Покажем, что еще одно выражение официальной физики:

                                               (5.1.8)

верно для релятивистской области. Если энергия частицы E₂>E₁, то можно записать, учитывая, что :

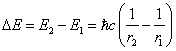                                    (5.1.9).

При тех же условиях:

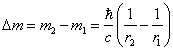                                   (5.1.10).

Умножив обе части (5.1.10) на c², получим (5.1.8).

Приведем без доказательства еще пару полезных соотношений:

 (нерелятивистская область) и

 (релятивистская область)                         (5.1.11).

Очевидно, что эти соотношения приравнивать друг другу нельзя.

5.1.1. Какая энергия соответствует формуле E=mc²

Ранее (глава 5.1) мы показали, что знаменитая формула:

E=mc²                                                                   (5.1.1.1)

является отражением максимально возможной кинетической энергии, которую имеет тело, движущееся со скоростью света. Она является суммой кинетической энергии движущегося по винтовой траектории тела в продольном и тангенциальном направлении. Никакого отношения к «энергии покоя» она не имеет, поэтому под массой в этой формуле следует всегда понимать релятивистскую массу, которая при малых скоростях может практически совпадать с массой покоя. В этой книге ясно показано, что масса любой частицы определяется ее составляющими, движущимися со световой скоростью, поэтому даже у «неподвижной» частицы масса всегда релятивистская, не релятивистской массы не существует. У ортодоксов считается, что формула (5.1.1.1) выражает максимально возможную полную энергию тела. Новая физика утверждает, что это максимально возможная кинетическая энергия тела, но потенциальная энергия тела может быть значительно больше.

Рассмотрим потенциальную энергию электростатического взаимодействия протона с ядром атома.

                                                               (5.1.1.2),

где e – элементарный заряд, Z – заряд ядра, r – расстояние от протона до центра ядра.

И заряд ядра, и расстояние от протона до центра ядра выразим через массу ядра.

В главе 12 показано, что внутренняя часть любого ядра представляет собой подобие кристаллической решетки в узлах которой находятся a-частицы, поэтому масса ядра выраженная через его заряд будет приблизительно (без учета дефекта массы) равна:

                                                        (5.1.1.3),

где m_p – масса протона, m_n – масса нейтрона.

Связь массы ядра с r очевидна:

                                                             (5.1.1.4),

где - ядерная плотность вещества (10¹⁴ г/см³).

Подставляя (5.1.1.3) и (5.1.1.4) в (5.1.1.2), мы найдем:

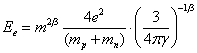                                             (5.1.1.5).

Подставим численные значения постоянных в системе СГС в формулы (5.1.1.1) и (5.1.1.5).

E=8,9875×10²⁰× m                                                          (5.1.1.6),

E_e=2,06265×10¹⁰× m^2/3 (5.1.1.7).

Подставим в (5.1.1.6) массу протона m_p=1,6726×10^-24 г, тогда его «энергия покоя» составит 1,5032×10^-3 эрг. Подставив это значение в (5.1.1.7) найдем, какова должна быть масса сверхядра, чтобы протон на его поверхности обладал потенциальной энергией равной его «энергии покоя»:

m_Z =1,7447×10^-9 г                                                          (5.1.1.8).

Новая физика предполагает возможность образования сверхядер массой до 6,63×10³⁴ г (глава 29.7.1), поэтому «энергия покоя» по формуле (5.1.1.1) может составлять лишь ничтожную часть полной энергии частицы. Здесь мы еще раз можем убедиться в том, что официальная физика манипулирует некоторыми понятиями, не имея ясного представления о том, что реально содержится в этих понятиях. Теперь становятся понятны те грандиозные энергетические явления на окраинах Вселенной, которые невозможно объяснить исходя из официальных представлений, связанных с формулой 5.1.1.1.

Здесь также необходимо раскрыть физический смысл «массы покоя» и «энергии покоя»:

E=m₀c²                                                             (5.1.1.9).

В теории элементарных частиц показано, что все они состоят в конечном счете из электронного нейтрино и антинейтрино, имеющих в свободном состоянии незначительную массу. При образовании частицы половина выделяющейся энергии идет на увеличение массы (она становится равной «массе покоя»), а половина на энергию связи. Энергия связи по теореме вириала будет численно равна энергии универсального отталкивания:

E_rep=m₀ c²/2                                                           (5.1.1.10),

поэтому суммарная энергия будет равна (5.1.1.9). Формулы (5.1.1.9) и (5.1.1.10) верны только для частиц, имеющих потенциальную яму гравидинамического взаимодействия. Эта потенциальная яма образуется при взаимодействии компонентов из гомоматерии (материи или антиматерии). При образовании частицы из гетероматерии (материя-антиматерия) потенциальная яма отсутствует (фотон), поэтому их энергия определяется формулой (5.1.1.1) и они всегда движутся в вакууме со скоростью света.

Энергия по формуле (5.1.1.9) – это скрытая энергия частицы, которая никак себя не проявляет до тех пор, пока мы сохраняем ее целостность. Аналогично внутриядерная энергия также скрыта до тех пор, пока ядро неизменно.

5.2. Релятивистский рост массы частицы.

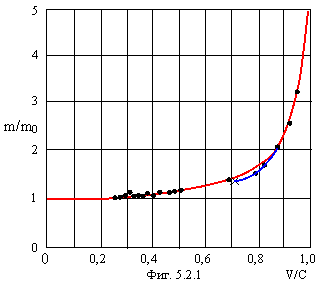
На фигуре 5.2.1 представлено отношение релятивистской массы к массе покоя электрона в зависимости от его скорости в долях от скорости света. Сплошная кривая соответствует известной формуле теории относительности:

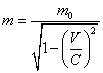                                            (5.2.1),

экспериментальные точки получены в 1901-1909 гг. График заимствован из книги Дж. Б. Мэрион «Физика и физический мир», «Мир», М., 1975, стр. 30.

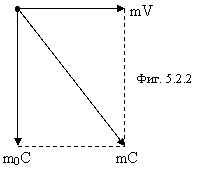
Сейчас мы покажем, что реальная ситуация с релятивистским ростом массы частицы гораздо сложнее, чем это представляется на фигуре 5.2.1. Формулу (5.2.1) легко получить из следующей схемы импульсов (фигура 5.2.2).

Эта схема пригодна для неподвижного электрона, который только собираемся двигать вправо по рисунку. Два нейтрино на орбите электрона каждый массой m₀/2 уже двигаются со скоростью света (как на орбите любых элементарных частиц), поэтому любые попытки перемещать электрон приводят к релятивистскому росту m₀. При этом движение электрона как целого по винтовой траектории никакого вклада в релятивистский рост массы не дает до тех пор, пока радиус этой траектории не станет равным r₀ по формуле (5.1.2). Поэтому на начальном участке графика фигуры 5.2.1 до поступательной скорости электрона  формула (5.2.1) будет верна. При указанной скорости электрон становится релятивистским, т.к. векторная сумма его поступательной и тангенциальной скорости на винтовой траектории равна скорости света. Этот момент обозначен крестиком на фигуре 5.2.1.

Здесь возникает интересная коллизия. Формулой (5.2.1) пользоваться уже нельзя, понятие какого-либо изменения скорости также непригодно в релятивистской области. Поэтому воспользуемся соотношением (5.1.8). Изменение энергии формально будет равно: E=mV² т.к. необходимо затратить одинаковую энергию mV²/2 на поступательное перемещение и тангенциальное. Изменение массы: m=m-m₀. Тогда (5.1.8) даст:

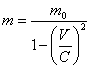                                           (5.2.2).

Полученная формула показывает, что когда электрон на винтовой траектории становится релятивистским, то релятивистское увеличение массы происходит значительно быстрее из-за того, что момент импульса электрона на винтовой траектории в 137 раз больше его собственного момента импульса. Все было бы именно так, если бы одновременно не уменьшалось значение m₀ по точно такому же закону, который предписывает выражение (5.2.1), т.е.:

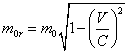                                        (5.2.3),

где m_0r - релятивистская «масса покоя» электрона в этой области. Из (5.2.3) видно, что в пределе, когда скорость электрона на винтовой траектории достигнет скорости света, «масса покоя» электрона станет нулевой. Физически это означает, что при одном обороте электрона по витку винтовой траектории нейтрино внутри электрона совершают тоже один оборот, т.е. электрон всегда повернут к оси винтовой траектории одной стороной, как Луна к Земле. Это обеспечивает условие, чтобы скорость частиц на орбите не превышала скорость света. Поскольку масса покоя компонентов релятивистской частицы становится равной нулю, чтобы найти энергию связи частицы, нужно из ее массы покоя вычесть массы покоя всех компонентов. Чтобы учесть выше изложенное, формулу (5.2.3) надо подставить в числитель (5.2.2). При этом с увеличением скорости числитель будет уменьшаться, а знаменатель уменьшается быстрее. После формального преобразования в итоге снова получим формулу (5.2.1), но теперь картина движения релятивистского электрона стала ясной и возникшая коллизия исчезла.

Когда скорость электрона становится равной скорости света, радиус винтовой траектории электрона равен по (5.1.2) 386,1594 фм. При этом формула (5.2.1) становится полностью непригодной для описания движения электрона. Действительно, из выражения для момента импульса электрона в релятивистской области:  найдем m и подставим в (5.2.1). После преобразований V/c=0 или V=0, что лишено физического смысла.

Здесь следует отметить, что формула (5.2.1) нами получена из чисто классического суммирования импульсов электрона по фигуре 5.2.2 и никакого отношения к так называемому фактору Лоренца 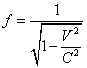 не имеет. Не имеет отношения и к специальной теории относительности. Мало того, в этой главе ясно показано, что формула (5.2.1) имеет ограниченную область применения до скорости поступательного движения электрона  и далее становится неприменимой. Тем не менее, официальная физика применяет фактор Лоренца, где надо и не надо, не понимая истинных физических явлений, скрытых за этим фактором. Истинная причина увеличения массы движущейся частицы состоит в том, что составляющие этой частицы (у электрона это нейтрино, см. главу 7.2) всегда движутся со скоростью света, поэтому для выполнения закона сохранения момента импульса масса растет обратно пропорционально радиусу орбиты компонентов частицы.

Вновь обратимся к фигуре 5.2.1. С увеличением поступательной скорости электрона увеличивалась и тангенциальная его скорость на витках винтовой траектории. Когда обе скорости достигли значения , суммарная скорость на траектории стала равной скорости света. При увеличении массы уменьшился радиус самого электрона и тут все ясно. В рассматриваемой точке фигуры 5.2.1 m=1,41m₀, V=C/1,41 перемножаем:  где r₀ - 386,134 фм. При дальнейшем увеличении поступательной скорости (до 0,866×С) радиус винтовой траектории уменьшается в 2 раза, из этой величины  идет на увеличение тангенциальной скорости и она становится равной скорости света, а еще  идет на увеличение массы электрона и она становится 2m₀. С этого момента увеличение поступательной скорости электрона приводит к уменьшению радиуса винтовой траектории («длины волны» электрона) и соответствующему увеличению массы mr=const. Уравнение (5.2.1) связи массы тела с его скоростью становится непригодным, а электрон полностью релятивистским. Далее более правильно связывать массу электрона с его «длиной волны» (энергией или радиусом винтовой траектории) а не с поступательной скоростью. Таким образом, область увеличения массы электрона от  до 2m₀ является переходной областью от Vr=const к mr=const и она обозначена на фигуре 5.2.1. синим цветом.

При поступательной скорости частицы V=0,866C она, как целое, движется по винтовой траектории с тангенциальной скоростью, равной скорости света, поэтому ее собственный момент импульса становится равным моменту импульса на винтовой траектории в не релятивистской области, а бывший собственный момент импульса становится равным нулю и вместе с ним станет равной нулю и бывшая «масса покоя» m₀. Здесь мы как бы вновь создали частицу из компонентов с нулевой «массой покоя», поэтому «новая» масса покоя будет вновь равна m₀ и формула (5.2.1) снова станет верной.

5.2.0.1. Релятивистская масса макротел

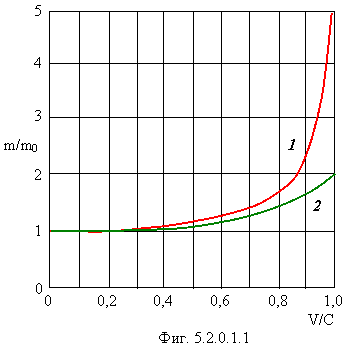
На фигуре 5.2.0.1.1 Кривая 1 показывает релятивистский рост массы отдельной микрочастицы в зависимости от ее скорости в соответствии с формулой:

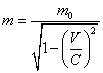                                                                (5.2.0.1.1).

Эта формула получена в результате анализа импульсов компонентов элементарной частицы (глава 5.2). Свободная элементарная частица движется по винтовой траектории в пространстве таким образом, что плоскость орбиты ее компонентов всегда перпендикулярна направлению движения. Это результат гравидинамического самовоздействия частицы.

В макротеле нет возможности анализировать направление импульсов каждой элементарной частицы из которой состоит макротело, т.к. плоскость орбиты компонентов частиц расположена хаотически и не перпендикулярна, в общем случае, направлению движения макротела. Свободно поворачиваться в пространстве она не может из-за внутренних связей в теле. Плоскость очень многих орбит в данный момент оказывается почти параллельной направлению движения тела и в этом случае релятивистского роста массы таких частиц не происходит, т.к. на одной половине орбиты масса растет, а на другой падает таким же образом. Поэтому подобные частицы практически не вносят вклад в релятивистский рост массы макротела. Кроме того, как для свободных элементарных частиц, так и для макротела, движение их по винтовой траектории по тем же причинам не влияет на рост массы, т.к. винтовое движение представляет собой независимые друг от друга поступательное перемещение и перпендикулярное ему тангенциальное движение. Поэтому релятивистский рост массы любых тел определяет только поступательная компонента их движения.

Для «неподвижного» макротела его масса определяется суммой масс всех частиц из которых тело состоит. Каждая из них представляет собой компоненты, вращающиеся со световой скоростью вокруг общего центра гравидинамического взаимодействия. Половина энергии гравидинамического притяжения компонентов при образовании частицы расходуется на универсальную энергию отталкивания, равную m_i×c²/2, где m_i – масса частицы, а вторая половина расходуется на энергию связи компонентов, которая в соответствии с теоремой вириала также равна m_i×c²/2. Если теперь найти общую энергию удаления компонетов каждой частицы на бесконечность (равную энергии гравидинамического притяжения) и суммировать ее по всем частицам тела, то мы получим знаменитую формулу энергии «покоя» тела: E₀=m₀ c². Очевидно, что при движении макротела к этой энергии надо прибавить кинетическую энергию поступательной компоненты движения: E_k=mV²/2, чтобы получить релятивистскую энергию макротела: mc²=m₀c²+mV²/2. Тогда релятивистский рост массы макротела в зависимости от поступательной скорости его будет определяться формулой:

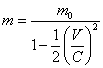                                                             (5.2.0.1.2),

график которой (2) изображен на фигуре 5.2.0.1.1. Обратите внимание на то, что релятивистский рост массы макротела при скорости его, равной скорости света, не может превысить 2m₀. Этот рост станет бесконечным только при движении макротела со скоростью . Именно эта скорость является максимально возможной скоростью движения тел. Именно с этой скоростью двигаются фотоны и частицы с «нулевой массой покоя», если сложить их поступательную и тангенциальную скорость на винтовой траектории. Интересно, что думает по этому поводу Эйнштейн и его последователи?

5.2.1. Световые скорости в новой физике

В новой физике представления о световых скоростях отличаются от официальных.

В главе 7.3. вводится понятие предельной скорости, которая немного превышает скорость света в вакууме, поэтому иногда полезней иметь в виду именно предельную скорость.

В главах 4-10 показано, что компоненты элементарных частиц двигаются по круговым орбитам со световой (предельной) скоростью, поэтому закон сохранения момента количества движения требует увеличения массы компонента с уменьшением радиуса его орбиты так, чтобы произведение m×r оставалось постоянным. Поэтому на круговой орбите частица может двигаться с предельной скоростью. Поскольку все свободные тела в природе двигаются по винтовой траектории, то с увеличением скорости движения радиус этой траектории уменьшается, что является причиной увеличения массы тела. Очевидно, что если бы тело могло достичь предельной поступательной скорости, то радиус винтовой траектории стал бы равен нулю, а масса тела бесконечной. Отсюда следует, что невозможно достичь предельную скорость при поступательном движении. В то же время скорость тела на витке винтовой траектории является векторной суммой поступательной и тангенциальной скорости и легко может преодолеть рубеж предельной скорости, приближаясь к значению C, где C – скорость света. Этот вывод говорит о том, что движение тел  является независимым по всем трем координатам пространства

5.2.2. Релятивистский рост массы электрона на атомной орбите

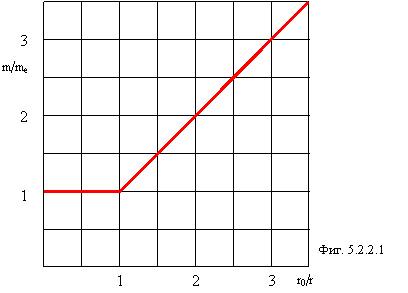
Официальная физика считает формулу релятивистского роста массы пригодной для всех случаев. Новая физика показала, что при орбитальном движении электрона его скорость может достигнуть скорости света при радиусе орбиты вокруг ядра r₀=386 фм (см. главу 5.1). При дальнейшем уменьшении радиуса орбиты скорость электрона остается неизменной, а масса растет по формуле:

                                                                          (5.2.2.1),

где: m – релятивистская масса электрона, m_e – масса не релятивистского электрона, r – радиус орбиты.

График релятивистского роста массы электрона на орбите представлен на фигуре 5.2.2.1 (сравни с фигурой 5.2.1).

Теперь интересно посмотреть, какой должен быть заряд ядра водородоподобного атома, чтобы электрон имел орбиту радиусом 386 фм. Для этого воспользуемся формулой (2.3) для радиуса орбиты в основном состоянии из главы 2: . Хотя это незаконно с точки зрения физического смысла, умножим числитель и знаменатель на m_e. Тогда в числителе окажется квадрат момента импульса электрона, но против математики мы при этом не согрешим:

                                                               (5.2.2.2).

Из (5.2.2.2) найдем Z:

                                                                 (5.2.2.3).

Но , где r_a – радиус первой боровской орбиты, поэтому:

                                                                    (5.2.2.4).

Подставив в (5.2.2.4) численные значения, найдем Z = 137.

Таким образом, релятивистский рост массы электрона на орбите любых мыслимых атомов невозможен, поэтому официальная физика делает очередную ошибку, когда учитывает этот рост.

Численное совпадение найденного заряда ядра с обратной величиной постоянной тонкой структуры не случайно. Дело в том, что скорость движения электрона на орбите Бора в 137 раз меньше скорости света. Чтобы достичь скорость света, нужно радиус орбиты электрона уменьшить в 137 раз, тогда в соответствии с формулой (5.2.2.2) заряд ядра нужно увеличить в 137 раз.

5.3. Ультрарелятивистская область

Предположим, что мы сообщили электрону такую большую энергию, что радиус винтовой траектории его уменьшился до того, что совпал с классическим радиусом самого электрона. В этом случае скорость электрона, начиная от радиуса, определяемого выражением (5.1.2) уже не меняется и равна с, а для выполнения закона сохранения момента импульса произведение mr должно оставаться постоянным:

                                                (5.3.1),

откуда:

=1,0545727×10^-27/2,81794092×10^-13×2,997924×10¹⁰=1248,314×10^-28г  (5.3.2).

Масса покоя электрона m₀=9,109390×10^-28 г. Следовательно, масса электрона на такой орбите, соответствующей орбите элементарных частиц, увеличится в:

m/m₀=137,03596 раз                                     (5.3.3),

т.е. соответствует величине, обратной постоянной тонкой структуры (137,0359895). Если (5.3.2) перевести в энергетические единицы (5,609586×10²⁶ Мэв/г), то получим значение единицы главного квантового числа (ГКЧ, см. элементарные частицы) в энергетическом выражении:

12,48314×10^-26 × 5,609586×10²⁶ = 70,02525 Мэв.                (5.3.4).

Можно посчитать массу электрона при сокращении радиуса винтовой траектории до r_e:

m = 0,5109991 × 386,1594 / 2,81794092 = 70,025281 Мэв         (5.3.5).

Наиболее точное энергетическое значение единицы ГКЧ можно получить, умножив энергию покоя электрона на обратную величину постоянной тонкой структуры 1 ГКЧ=70,0252673 Мэв.                                                           

Поскольку частицы в свободном состоянии обладают моментом импульса , очевидно, что «возбужденные» квантовые состояния данной частицы будут кратны этой величине. Следовательно, энергетические уровни элементарных частиц будут кратны 70,025 Мэв или половине этого значения, если орбитальный момент импульса какого-либо компонента равен /2.

5.4. Методика расчета радиусов орбиты, энергии связи, магнитного момента и масс элементарных частиц

Как найти энергию связи элементарной частицы, было изложено в разделе 5.2, здесь только необходимо добавить, что в энергии связи нужно учитывать также электростатическое взаимодействие компонентов частицы, хотя оно существенным образом не влияет на энергию связи.

Общий момент импульса частицы в целом (главное квантовое число ГКЧ) N равен сумме моментов импульса компонентов на орбите этой частицы:

                                           (5.4.1),

поэтому расчетная масса любой частицы на орбите равной радиусу электрона равна:

m_cal =N×70,0252673 Мэв                                    (5.4.2).

Если значение m_cal отличается от реальной массы частицы более чем на 35 Мэв, то это означает, что наши предположения о строении элементарной частицы требуют уточнения или неверно определено ГКЧ.

Сравнивая расчетное значение массы с экспериментальным значением, можно сделать выводы о дополнительном отталкивании или притяжении компонентов, которое увеличивает или уменьшает радиус орбиты и приводит к уменьшению или увеличению реальной массы частицы.

Радиус любой элементарной частицы

                                               (5.4.3),

где m – опытная масса частицы. Если это масса покоя частицы, то (5.4.3) даст уточненное значение радиуса орбиты компонентов частицы, по которому можно судить о взаимодействии этих компонентов или обратной подстановкой в (5.4.3) найти точное значение массы частицы.

Очевидно, что большинство элементарных частиц будет иметь радиус, близкий классическому радиусу электрона. Для расчетов в микромире удобно пользоваться единицей расстояния: 1 фм=10^-13 см и единицей массы, выраженной в Мэв: 5,609586×10²⁶ Мэв/г. 1 Мэв=1,60206×10^-6 эрг.

Подставим эти значения в (5.4.3) и получим выражение, где масса выражена в Мэв, а радиус в фм, которым удобно пользоваться для любого компонента частицы или частицы в целом:

                                       (5.4.4).

Магнитный момент частиц рассчитывают по формуле:

                                               (5.4.5),

где  - магнитный момент в эрг×гс^-1, e – электрический заряд в единицах СГСЭ, m – масса частицы, c – скорость света. Подставив в (5.4.5)  для релятивистской области и  для не релятивистской области, после преобразования, найдем выражения, которые не зависят от масс частиц:

                                                (5.4.6),

для не релятивистских частиц и:

                                                  (5.4.7)

для релятивистских частиц.

Например, для электрона в не релятивистской области по (5.4.7) = 0,9274015×10^-20 эрг×гс^-1. К этому значению еще надо прибавить собственный магнитный момент электрона, но поскольку нейтрино, образующие электрон релятивистские, то нужно использовать (5.4.7) подставляя в него классический радиус электрона: = 0,006767576×10^-20 эрг×гс^-1. Складывая оба значения, получим: = 0,934169×10^-20 эрг×гс^-1. Отношение магнитного момента свободного электрона к магнетону Бора будет: /= 1,007297271. По мере увеличения скорости электрона радиус винтовой траектории уменьшается, собственное вращение нейтрино в электроне также замедляется. При достижении минимального не релятивистского радиуса винтовой траектории 386,1594×10^-13 см за один оборот электрона на траектории нейтрино в нем также делают один оборот, т.е. электрон движется как твердое тело и дополнительного вклада в магнитный момент не вносит. Тогда из (5.4.7): = 0,9274017×10^-20 эрг×гс^-1. В этом случае отношение магнитного момента электрона к магнетону Бора будет: /= 1,0000002. Таким образом, магнитный момент электрона с увеличением его скорости падает и когда он становится релятивистским, его магнитный момент совпадает с магнетоном Бора. При дальнейшем увеличении энергии электрона его радиус винтовой траектории обратно пропорционален энергии, соответственно и магнитный момент будет резко уменьшаться. Например, при энергии электрона 70,0252673 Мэв (радиус винтовой траектории равен классическому радиусу электрона), его магнитный момент по (5.4.7) будет: = 0,006767576×10^-20 эрг×гс^-1, т.е. совпадать с собственным магнитным моментом свободного электрона. Тогда отношение магнитного момента такого электрона к магнетону Бора составит: / = 0,00729735. Таким образом, магнитный момент частиц не является постоянной величиной, а меняется в зависимости от радиуса винтовой траектории частицы или радиуса орбиты в составе других частиц.

Экспериментально найденный магнитный момент электрона  немного больше магнетона Бора  в 1,0011616 раза. Официальная физика считает магнитный момент электрона аномальным (он должен быть равен магнетону Бора) и привлекает для его объяснения представления о взаимодействии электрона с виртуальными частицами вакуума: “Аномальный магнитный момент электрона. Радиоспектроскопические исследования показали, что магнитный момент электрона не равен в точности одному магнетону, а несколько больше. Квантовая электродинамика показала, что возрастание магнитного момента электрона обязано взаимодействию электрона с вакуумом (физическим пространством)”. Н.И. Карякин и др., “Краткий справочник по физике”, “Высшая школа”, М., 1962, стр. 354.

Для новой физики очевидно, что двигающийся по винтовой траектории электрон с моментом импульса  создаст магнитный момент, равный магнетону Бора плюс часть собственного магнитного момента электрона (с моментом импульса ). Если бы электрон двигался по винтовой траектории со световой скоростью (как фотон), то он был бы повернут к оси этой траектории всегда одной стороной, т.е. двигался бы как твердое тело. В этом случае собственный магнитный момент электрона давал бы нулевой вклад в общий момент, т.к. обметаемая зарядами нейтрино площадь равна нулю. В этом случае магнитный момент электрона был бы в точности равен магнетону Бора. Поскольку нейтрино в электроне движутся со световой скоростью, а сам электрон по винтовой траектории со значительно меньшей скоростью, то траектория отдельного нейтрино будет представлять собой разновидность эпициклоиды с обметаемой площадью “электрического тока” , а не , а общий магнитный момент соответствовать экспериментально найденному. Это значение совпадает с поправкой Ю. Швингера к магнитному моменту электрона: (/2).

Если бы мы механически сложили магнитный момент электрона на винтовой траектории с собственным магнитным моментом, равным /137,0391=0,0072971×, то в итоге получили бы завышенный общий момент =1,0072971×. Кстати сказать, магнитные моменты большинства частиц “аномальны”, например, у нейтрона и протона. Причем аномальность последних не укладывается в теоретические представления ортодоксальной физики, разработанные для электрона, что служит подтверждением ошибочности их.

С магнитным моментом электрона нужно разобраться подробнее, т.к. представления новой физики резко отличаются от официальной физики в этом вопросе. Рассмотрим вначале нерелятивистский электрон. Для этого случая будем пользоваться формулой (4.5) по которой магнитный момент электрона, движущегося по винтовой линии, будет:

                                           (5.4.8),

где V – тангенциальная скорость электрона (равная поступательной), C – скорость света, e – элементарный заряд, R – радиус винтовой траектории. Момент импульса электрона на винтовой траектории:

                                             (5.4.9),

где m₀ – масса покоя электрона. Подставив (5.4.9) в (5.4.8), найдем, что магнитный момент электрона в этом случае равен магнетону Бора:

                                       (5.4.10).

Теперь рассмотрим релятивистский электрон. Для этого случая будем пользоваться формулой (4.4). Аналогичные выкладки, учитывая, что при этом

                                             (5.4.11)

дадут:

                                           (5.4.12),

т.е. магнитный момент релятивистского электрона  будет уже зависеть от его массы и уменьшаться с увеличением энергии электрона. Формулу (5.4.12) можно получить иначе. Релятивистский электрон вращается на винтовой линии как твердое тело, делая один оборот вокруг своей оси за один оборот по винтовой траектории, из-за невозможности составляющих его нейтрино двигаться со сверхсветовой скоростью. Поэтому можно записать для первого (наружного) нейтрино, учитывая, что заряд нейтрино равен e/2: , где r – радиус электрона. Для второго (внутреннего) нейтрино: . Сумма моментов будет , откуда, выражая R через момент импульса электрона (5.4.11) получим (5.4.12). Следует иметь в виду, что в релятивистском электроне не только уменьшается длина волны де Бройля (радиус и шаг винтовой траектории), но уменьшаются и размеры самого электрона, поэтому магнитный момент релятивистского электрона не является фиксированной величиной, как это представляется официальной физике. Теперь найдем собственный магнитный момент нерелятивистского электрона, учитывая, что нейтрино в электроне движутся со скоростью света:

                                      (5.4.13).

Подставляя в (5.4.13) значения

                                                (5.4.14)

  - постоянную тонкой структуры и классический радиус электрона

                                            (5.4.15),

найдем , т.е. собственный магнитный момент электрона в 137 раз меньше магнитного момента на витках винтовой траектории. Собственный механический момент электрона, очевидно, равен:

S_own= m₀Cr₀                                           (5.4.16).

Отношение магнитного момента (5.4.13) к механическому (5.4.16) составит:

                                          (5.4.17).

Подставив (5.4.15) в (5.4.13) и полученное выражение для  в (5.4.17), найдем:

                                              (5.4.18).

Отношение собственного механического момента (5.4.18) к механическому моменту на винтовой траектории  дает выражение (5.4.14), что естественно. Формула (5.4.18) дает ответ на загадку происхождения электрического заряда  - электрический заряд напрямую связан с наличием момента импульса нейтрино в электроне или позитроне, в конечном итоге, с наличием момента импульса самого нейтрино (смотрим также Комментарии автора к главе 7.1: 1. Вещество и антивещество). Таким образом, общий магнитный момент "теплового" свободного электрона равный (1+) = 1,007297 больше, чем официально признанный 1,0011616 и полученный из спектроскопических данных (почти релятивистский электрон) и уменьшается обратно пропорционально энергии электрона. Экспериментальное подтверждение этого поставит современную квантовую механику в затруднительное положение.

5.5. Электрон (позитрон) и нейтрино

Строение электрона (позитрона) уже рассмотрено достаточно подробно. Если электрон находится на орбите какой-либо частицы, то он сохраняет значение момента импульса свободного электрона . Если радиус орбиты равен классическому радиусу электрона, то его масса возрастает до 70,025 Мэв. При этом размер самого электрона на такой орбите уменьшается в 70,0252673 / 0,5109991 = 137,0359895 раз и становится равным 2,81794092 / 137,0359895 = 0,02056351 фм. Электронные нейтрино, образующие электрон точно так же уменьшаются в размерах, а масса каждого нейтрино становится равной 35,01263365 Мэв (). По сравнению со свободным электроном и свободным нейтрино (основное состояние) их состояние на орбите с радиусом равным классическому радиусу электрона – это их первое возбужденное состояние N=1. При N=2,3,4… масса электрона будет увеличиваться в число раз, кратное 70,0252673 Мэв, а масса нейтрино увеличится в число раз, кратное 35,01263365. Поскольку закон сохранения момента импульса требует, чтобы произведение mr оставалось постоянным, то радиусы орбит в зависимости от ГКЧ будут определяться выражением:

                                       (5.5.1).

Из (5.5.1) видно, что при N=0 (основное состояние) радиус движения частицы бесконечно большой, но при сохранении момента импульса (обычно ), скорость движения будет равна нулю. При бесконечно большом N (бесконечно большой массе и энергии частицы) r_N 0.

Формальное значение ГКЧ легко найти, разделив массу интересующей нас частицы (в Мэв) на энергетическое содержание единицы ГКЧ (70,0252673 Мэв). Если получается близкое к целому значение N, то количество нейтрино в частице четно, если близкое к полуцелому значению – нечетно. Однако в действительности энергетические уровни частиц почти никогда не подчиняются в точности выражению (5.5.1). Отличия будут небольшие и обусловлены электростатическим взаимодействием и разным взаимодействием гомоматерии (материя-материя, антиматерия-антиматерия) и гетероматерии (материя-антиматерия). Таким образом, указанные взаимодействия расщепляют уровни энергии, определяемые выражением (5.5.1) на ряд подуровней в зависимости от конкретного строения частицы и значения N, поскольку при разном N компоненты находятся на разном расстоянии друг от друга, а их взаимодействие не пропорционально расстоянию.

Поскольку для орбитального движения частицы со скоростью света:

                                             (5.5.2),

то:

                                            (5.5.3),

где m – масса частицы на орбите радиуса r, а m₀ и r₀, соответственно, масса частицы и радиус орбиты сравнения, на которой эти величины известны или формально определены, например, по формуле (5.1.5). Пользуясь (5.5.3) всегда можно внести необходимые поправки с учетом точного положения энергетического подуровня. Например, масса мюона 105,658387 Мэв. Через 2,19703×10^-6 сек он распадается с вероятностью около 100% на электрон, электронное антинейтрино и мюонное нейтрино. Разделив массу мюона на 70,0252673 Мэв, найдем формальное значение N_ф=1,508861. Расчетная масса мюона из таблицы 5.5.1 будет:

m_р = 70,0252673 + 0,25549955 + 35,01263365 = 105,2934005 Мэв.

Откуда расчетное значение ГКЧ: N_p=1,503649. В (5.5.3) можно пользоваться отношением формального и расчетного значения ГКЧ:

r=2,81794092×1,503649/1,508861=2,80820702 фм. Мы получили уточненный радиус мюона. Он немного меньше классического радиуса электрона, что указывает на некоторое притяжение между компонентами мюона. Увеличение радиуса указывало бы на некоторое отталкивание. С учетом полученного радиуса орбиты (5.5.3) даст значение массы мюона, точно совпадающее с экспериментальным значением. Таким же образом находят радиусы любых других элементарных частиц в состоянии покоя. При движении частицы, как целое радиус ее уменьшается и легко подсчитать его для релятивистских и ультрарелятивистских частиц.

Характеристики электрона (позитрона) и нейтрино представлены в таблице 5.5.1.

Таблица 5.5.1.

Частица	Электрон	Электронное нейтрино	Мюонное нейтрино
Момент импульса свободной частицы		/2×137,035989
Масса свободной частицы, Мэв	0,5109991	4,828558 эв	661,68623 эв
Масса в составе электрона, Мэв	-	0,25549955	-
Масса при движении по орбите с радиусом электрона N=1, Мэв	70,0252673	0,25549955	35,01263365
Масса при N=2, Мэв	140,0505346	0,5109991	70,0252673
Радиус свободной частицы, фм	2,81794092	Зависит от энергии	Зависит от энергии
Радиус связанной частицы	Обратно пропорционален массе	Обратно пропорционален массе	Обратно пропорционален массе

Примечание к таблице 5.5.1. Чтобы найти массу свободных нейтрино, нужно учесть, что они двигаются со скоростью света в свободном состоянии, тогда, например, масса электронного нейтрино будет:

0,25549955 / 137,035989 × 386,134 = 4,828558×10^-6 Мэв, а масса мюонного нейтрино: 35,01263365 / 137,035989 × 386,134 = 661,686230×10^-6 Мэв.

Ранее было найдено, что радиус свободного электронного нейтрино равен половине радиуса винтовой траектории его.

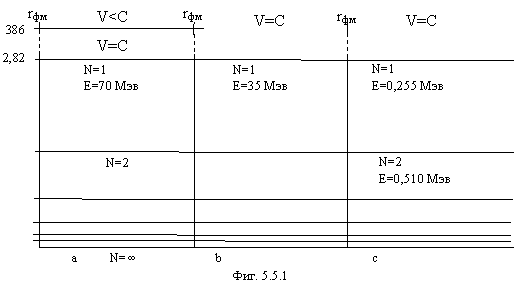
На фигуре 5.5.1 изображены энергетические уровни электрона (а), мюонного нейтрино (b) и электронного нейтрино (c) в зависимости от N.

5.5.1. Сверхтекучесть и сверхпроводимость

Поскольку момент импульса электрона на витках винтовой траектории не может меняться - он или есть, или его нет, то при сверхнизких температурах (или в условиях лишения электрона его момента импульса) мы должны наблюдать скачкообразное изменение свойств веществ так или иначе связанных с наличием свободных электронов. При нормальных температурах таких эффектов можно достичь, лишая электроны возможности двигаться по винтовой линии, например, в сверхтонких проводниках, радиус которых значительно меньше длины волны де Бройля электрона при данной температуре. Примером такой сверхпроводящей рамки с током служит молекула бензола.

Сверхтекучесть и сверхпроводимость с точки зрения новой физики имеют одну и ту же причину - утрату частицами момента количества движения по виткам винтовой траектории.

В первом случае - это потеря момента атомами гелия, а во втором - электронами (= 0). Вся проблема в том, кому передать этот момент.

Атомы гелия передают его атомам стенок сосуда, в котором находится жидкий гелий, поэтому наблюдается фазовый переход второго рода, и в жидком гелии находятся как бы две жидкости, у которых движение атомов принципиально различно. В гелии I они движутся по отрезкам винтовых линий, а в гелии II - по прямой. Таким образом, не противореча наиболее адекватной опытам двухжидкостной модели сверхтекучести современной физики, новая физика делает те же выводы, не привлекая официальную квантовую механику. Переход жидкого гелия в сверхтекучее состояние не сопровождается тепловым эффектом (фазовый переход второго рода или l-переход), т.к. при потере атомом гелия момента импульса на винтовой траектории данный атом становится "холодным", но его энергия передается соседним атомам и в целом теплового эффекта не наблюдается из-за закона сохранения энергии. Однако, поскольку гелий в состоянии сверхтекучести представляет собой смесь "холодной" (с отсутствием у атомов момента импульса) и "горячей" (с сохранившимся у атомов моментом импульса) жидкости, то наблюдается механокалорический эффект. При вытекании HeII из сосуда через узкий капилляр в сосуде повышается температура и, наоборот, в месте втекания HeII из капилляра в другой сосуд происходит охлаждение. При переходе гелия в сверхтекучее состояние, его теплопроводность увеличивается, примерно, в 10⁶ раз и механизм теплопроводности отличается от обычного по многим признакам. Этот эффект также очевиден: атомы лишенные момента импульса подобны электронам сверхпроводимости.

Изложенная причина сверхтекучести гелия дает возможность влиять на этот эффект добавками в жидкий гелий молекул, которые в целом или их части не прочь заполучить момент количества движения атомов гелия. Очевидно, что получить эффект сверхтекучести при нормальных температурах невозможно, т.к. потенциальные приемники момента импульса не столько отбирают его у атомов, сколько награждают им. По-видимому, только пропусканием атомов сквозь каналы, поперечник которых заведомо меньше диаметра винтовой траектории можно добиться каких-то успехов. То же касается и сверхпроводимости в случае движения заряженных частиц. В этой связи есть смысл выдвинуть гипотезу, согласно которой в биологических объектах за долговременную память ответственны замкнутые электрические токи сверхпроводимости, реализуемые при нормальных температурах в молекулярных каналах. Для ³He связь между атомами сильнее, чем связь между атомами ⁴He за счет нескомпенсированного магнитного момента атомов, поэтому потеря момента импульса атомами ³He затруднена, т.к. им приходится взаимодействовать сразу со многими соседями с большой эффективной массой (по измерениям теплоемкости m_эф=3,1m). Поэтому температура перехода ³He в сверхтекучее состояние ниже (0,01⁰К), чем у ⁴He (2,1⁰К). Для объяснения сверхтекучести ³He официальная физика прибегает к образованию куперовских пар уже из атомов ³He, считая их фермионами. Очевидно, что при образовании куперовских пар система в целом переходит в более выгодное энергетическое состояние и этот процесс должен сопровождаться выделением тепла, т.е. должен наблюдаться фазовый переход первого рода, что не соответствует экспериментальным данным.

Электроны передают свой момент  дефектам кристаллической решетки или атомам “примеси”, а также атомам основной кристаллической решетки, если больше нет ничего подходящего. Поэтому температура перехода в сверхпроводящее состояние монокристаллов чистых элементов очень мала. Физика микромира, “Советская энциклопедия”, М., 1980, стр.335.

 С точки зрения ортодоксальной физики переквалификация электронов из индивидуалистов-фермионов (=1/2) в колхозников-бозонов (=0) совершенно невозможна в то время, как новая физика считает, что неразличимые по моменту импульса электроны (у всех =1) стали различимы (часть имеют =1, а часть =0), т.е. состояние “электронного газа” при сверхпроводимости подобно двухжидкостной модели сверхтекучести.

Эффект Джозефсона по представлениям новой физики прямо подтверждает потерю электронами момента количества движения в явлении сверхпроводимости. Эффект наблюдается при прохождении сверхпроводящего тока через слой диэлектрика или слой металла в нормальном состоянии или в сверхпроводниках с сужением (точечные контакты). Если ток превышает некоторое критическое значение, то возникает падение напряжения U и излучаются фотоны с энергией h=2eU. Официальная физика считает, что фотоны излучаются куперовскими парами электронов, которые возбуждаются, а затем излучают, переходя в нормальное состояние. Такое представление вызывает серьезные возражения: 1. На участке падения напряжения сверхпроводимость отсутствует, поэтому куперовские пары на этом участке отсутствуют. 2. Неясно, каким образом два электрона куперовской пары одновременно могут излучить один фотон с суммарной избыточной энергией обеих электронов. 3. Учитывая, что расстояние между электронами куперовской пары составляет 10^-4 см, то между ними находится огромное количество других электронов, принадлежащих другим парам. В этом случае излучение данной куперовской парой фотона с энергией 2eU кажется еще более невероятным. 4. Поскольку куперовские пары все время исчезают и появляются вновь, то непонятно, как вновь рожденная пара воспринимает возбужденное состояние предыдущей, чтобы в итоге накопить избыточную энергию 2eU . Новая физика объясняет эффект Джозефсона просто и без противоречий.

Схема эффекта приведена на рисунке 5.5.1.1, где 1 – сверхпроводник, 2 – участок нормальной проводимости с падением напряжения на концах U. Электрон в сверхпроводящем состоянии не имеет момента количества движения  (движется прямолинейно) радиус его траектории равен классическому радиусу электрона    2,8·10^-13 см, поэтому кристаллическая решетка сверхпроводника для него является практически пустым пространством. Назовем такой электрон "холодным". Когда этот электрон попадает на участок нормальной проводимости, он приобретает момент импульса  от ионов кристаллической решетки и его траектория становится винтовой с радиусом 2,3·10^-8 см (средняя скорость теплового движения электрона при температуре близкой к абсолютному нулю около 500 км/сек). Такой электрон назовем "горячим". Хотя электроны из-за своей незначительной массы практически не вносят вклад в теплоемкость твердого тела, тем не менее, на участке появления "горячих" электронов должно поглощаться немного тепла за счет уменьшения энергии ионов. На участке нормальной проводимости электрон приобретает энергию за счет увеличения поступательной скорости . Но такую же энергию он приобретет и за счет увеличения тангенциальной скорости на витках винтовой линии. Общее увеличение энергии при движении в электрическом поле составит mV² =2eU. Попадая вновь на участок сверхпроводимости "горячий" электрон вновь становится "холодным" за счет потери момента импульса на ионах кристаллической решетки. При этом тепло выделяется. Кроме того, его избыточная энергия или излучается фотоном с энергией 2eU или рассеивается на ионах без излучения. При переходе в сверхпроводящее состояние возникает парадоксальная ситуация: чем больше электрическое сопротивление проводника, чем больше его неоднородность, тем легче электрону потерять момент импульса и стать "холодным", поэтому хорошо проводящие металлы (серебро и др.) не обладают сверхпроводимостью. Кроме того наблюдается так называемый изотопический эффект сверхпроводимости: , где T_k – критическая температура перехода в сверхпроводящее состояние, а M – масса изотопа. При прочих равных условиях (в образцах изотопов одного и того же элемента) более легким ионам проще принять момент импульса электрона, чем тяжелым, поэтому образование "холодных" электронов облегчается.

Поскольку механизм образования куперовских пар противоречит основам квантовой механики в части, касающейся строения атома, проанализируем представления официальной физики по куперовским парам немного подробнее. Куперовские пары электронов при сверхпроводимости обусловлены обменом двух электронов фононами (это квазичастицы – фактически звуковые волны). Таким образом, официальная физика отрывает колебания кристаллической решетки от самой решетки и этой уже не имеющей физического смысла фикцией связывает электроны между собой. Каким образом звуковые волны могут приводить к притяжению электронов да еще превышающему дальнодействующее кулоновское отталкивание? Почему обмен фононами приводит к притяжению, а не к отталкиванию? Полный импульс куперовской пары равен нулю. В пары связываются электроны с противоположным импульсом. Как могут связаться электроны посредством фононов, если их скорость теплового движения примерно на два порядка превышает скорость фононов – скорость звука в металле, да и движутся они в противоположные стороны? Поскольку куперовские пары электронов становятся по представлениям официальной физики бозонами, то все они могут находиться в одинаковом основном состоянии. По этой же логике пара S-электронов в атоме тоже бозон, поэтому все электроны в атоме должны попарно занять основное состояние, чего на самом деле не происходит.

Потеря электронами момента импульса сопровождается и другими эффектами, например, эффектом Мейсснера – сверхпроводник становится идеальным диамагнетиком и внешнее магнитное поле внутри его отсутствует. Это связано с тем, что "холодные" электроны идеально следуют закону Ленца и за счет действия силы Лоренца движутся по окружности, компенсируя внешнее поле. "Горячие" электроны движутся по винтовой траектории и не могут полностью компенсировать внешнее магнитное поле. При потере момента импульса электроны теряют сразу семь степеней свободы из 10 (см. главу "Рождение и смерть фотона"), поэтому, чтобы вернуть их в нормальное состояние необходима энергия 3,5kT_c. "Существование такой щели (энергетической в сверхпроводнике), имеющей при Т 0 ширину около 3,5kT_c (где T_c – температура перехода в сверхпроводящее состояние) постепенно сужающейся при повышении температуры и исчезающей при T T_c, было установлено по внезапному изменению поглощения далекого инфракрасного (или микроволнового) излучения в сверхпроводнике в тот момент, когда энергия квантов этого излучения h становилась равной ширине щели". Р. Спроул, Современная физика, М., 1974, стр.313.

Внешнее магнитное поле провоцирует приобретение электронами момента импульса за счет силы Лоренца и при достаточной напряженности поля сверхпроводимость исчезает. Очевидно, что энергия, сообщенная внешним полем должна составлять, например: 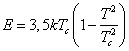, чтобы сверхпроводимость исчезла. Зависимость критического внешнего магнитного поля от температуры меняется так же, как и энергия E (см., например, Физика микромира, М., 1980, стр. 335 и 347). Известно, что без внешнего поля явление сверхпроводимости не сопровождается тепловым эффектом. С точки зрения новой физики это понятно, т.к. электроны, потерявшие момент импульса, передают энергию кристаллической решетке, и система в целом не теряет и не приобретает энергию. У официальной физики здесь возникает проблема, т.к. при образовании куперовских пар вся система в целом переходит в более энергетически выгодное состояние, что должно сопровождаться выделением тепла. При наличии внешнего магнитного поля тепловой эффект уже будет и должен в точности соответствовать дополнительной энергии E.

Здесь следует обратить особое внимание читателя, что ток в сверхпроводящем кольце наблюдается без изменений в течение очень длительного времени. По классической электродинамике равномерно движущийся по окружности заряд должен излучать электромагнитные волны и ток быстро прекратится. Таким образом, классическая электродинамика в вопросе излучения электромагнитных волн ошибочна. Современная физика, повторяя эту ошибку, отвергла теорию атома Бора и пошла по пути наслоения ошибок друг на друга.

5.6. Протон и фотоны

Протон имеет три частицы: позитрон и два фотона (или, что эквивалентно, два позитрона и электрон), следовательно, для протона N=3, т.к. на орбите каждая частица имеет момент импульса . Строение частиц будет показано отдельно. Подставляя в (5.4.4) значение массы протона m=938,2723 Мэв, найдем его радиус: r_p=0,6308 фм. Поскольку радиус орбиты компонентов протона сократился по сравнению с «нормальным», равным классическому радиусу электрона за счет гравидинамического взаимодействия в: 2,81794092 / 0,6308 = 4,46725 раз, то масса этих компонентов возросла во столько же раз, чтобы удовлетворить закон сохранения момента импульса:

70,025 × 4,46725 = 312,819 Мэв                              (5.6.1),

а масса протона в целом будет 312,819 × 3 = 938,4575 Мэв, что означает, что внутри протона действует незначительное дополнительное отталкивание. Оно обусловлено тем, что положительно заряженные антинейтрино в фотонах и в позитроне смотрят к оси вращения, т.е. расстояние между положительными электрическими зарядами немного меньше. Теперь мы можем найти радиусы позитрона и фотона (или электрона) внутри протона и, таким образом, уточнить его строение по формулам (5.5.2) и (5.5.3).

Подставляя в (5.5.3) r₀=2,81794092, m₀=0,5109991 Мэв, m=312,819 Мэв, найдем: r=0,0046032 фм. Таким образом, радиус позитрона или фотона в протоне уменьшается в 612,17 раз. В таком же соотношении уменьшаются радиусы нейтрино, образующие позитрон и фотон. Таким образом, протон такой же «пустой», как Вселенная, галактика, атом или мы с вами. Вместе с тем огромный гравидинамический момент протона организует движение частиц вокруг (барионы) в одной плоскости, аналогично тому, как гравидинамическое ядро образует спиральную галактику или вращающаяся звезда плоскую спутниковую систему. Отношение расчетной к реальной массе протона составляет:

m_p/m=1,000198, уточненный радиус протона: 1,000198×0,6308=0,630925фм.

Характеристики протона представлены в таблице 5.6.1.

Таблица 5.6.1.

Частица	Момент импульса свободной частицы	Масса свободной частицы, Мэв	Масса в составе протона, Мэв (N=1)	Масса при N=2, Мэв	Радиус свободной частицы, фм	Радиус связанной частицы, фм
Протон		938,2723	-	1876,5446	0,630925	-
Позитрон		0,5109991	312,819	625,638	2,81794092	0,0046032
Фотон		Зависит от энергии	312,819	625,638	Зависит от энергии	0,0046032

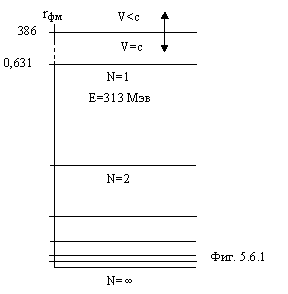
Энергетические уровни протона показаны на фигуре 5.6.1.