Содержание
1. К читателю
2. Реальные процессы и необходимость в новых исчислениях.
3. Определение новых исчислений аналогичных дифференциальному и интегральному (D-исчисления).
4. D-дифференциальное исчисление.
5. D-интегральное исчисление.
6. D-дифференциальные уравнения.
7. Примеры применения новых исчислений.
Когда я учился в школе, и после арифметики стали преподавать алгебру, наша учительница, не посвятив учеников, чем занимается алгебра и зачем она нужна, сразу взяла быка за рога и начала на доске писать a+b=c+d и тому подобное. Сначала сложилось впечатление, что алгебра – глупая наука, но прошло некоторое время, и я понял, что глупа не алгебра, а наша учительница. Надо было сразу объяснить, что существуют некоторые общие правила действия над цифрами и тогда удобнее не называть 5 яблок или просто цифру 5, а под «a» или «b» понимать любые цифры или однородные объекты. В предыдущих изданиях книги я уподобился той глупой учительнице и сразу излагал суть новых исчислений, не удосужившись объяснить, что они собой представляют и для чего нужны.
В настоящее время дифференциальное и интегральное исчисление единственное в своем роде. Оно изучает, как влияет изменение аргумента на скорость того или иного процесса или, наоборот, как по изменению скорости найти изменение самой функции. Многие задачи с точки зрения дифференциального исчисления нам понятны и легко решаются, например задача движения тела с равномерно увеличивающейся скоростью. Многие задачи легко перевести в удобный для дифференциального исчисления вид, многие – трудно и это дело требует высокой квалификации, а многие – невозможно. Вместе с тем, часто встречаются задачи, физический смысл которых нам ясен, но «математизировать» их достаточно сложно. Например, для нас очевидно, что если какой-то микроб через определенное время удваивается, то по прошествии этого времени общее число микробов будет в два раза больше исходного числа. В данном случае нам помогло бы исчисление в виде y/y-1=2, где y – текущее значение функции, y-1 – предыдущее значение функции. Наши мозги устроены таким образом, что мы можем здраво размышлять, сравнивая текущее значение некоторой величины с ее предыдущим значением. На этом основаны наши прогностические способности и здесь мы достигаем больших успехов, даже ничего не зная о причинах изменения обсуждаемой функции. Предлагаемые исчисления предназначены для поддержки этих способностей и оперируют с текущими и предыдущими значениями любых процессов. Причем эти значения могут меняться не только во времени, но и под действием любых аргументов.
2. Реальные процессы и необходимость в новых исчислениях
В настоящее время на практике используется весьма несовершенная методика математического описания какого-либо процесса. Составляют исходную систему уравнений, которые (по предположению исследователя) более или менее адекватно отражают реальный процесс. Этой системе уравнений задают начальные условия или параметры и затем решают ее численными методами, т.к. аналитическое выражение зачастую получить невозможно. Полученные результаты сравнивают с практически наблюдаемыми и в случае значительного несогласия с наблюдательными данными вносят коррективы в исходную систему уравнений. При этом исходная система уравнений быстро усложняется (упроститься она принципиально не может) и после нескольких попыток получить приемлемое решение, вынуждает исследователя идти на компромисс, жертвуя и точностью и здравым смыслом исходной системы уравнений.
Всякий реальный процесс в любой определенный момент своего развития «не знает» ни своей истории, ни своего будущего. Он развивается на основе существующих условий в этот момент, сложившихся в течение данного процесса или еще до его начала. Очевидно, что любой процесс при изменении условий его протекания пойдет с другой скоростью или даже в другом направлении, поэтому задание начальных условий не совсем правильно, т.к. реальному процессу на них, по большому счету, наплевать. Кроме того, изменится протекание и других, побочных процессов, сопровождающих исследуемый процесс. Термин «условия», в которых протекает процесс не совсем удачен по той причине, что всегда условий можно найти или перечислить очень много, а на данный процесс влияют только некоторые из них и в разной степени. Поэтому есть смысл ввести понятие ресурса процесса. Ресурс процесса – это условия, непосредственно влияющие на данный процесс, ускоряя его или замедляя. При неограниченном ресурсе или ресурсе, имеющем постоянное значение, его можно не учитывать, т.к. ход процесса в этих условиях не меняется. Рассмотрим несколько примеров.
1. Предположим, что мы изучаем рост культуры микроорганизмов в условиях неограниченной поставки питательных веществ и удаления продуктов жизнедеятельности. Кроме того, объем инкубатора также неограничен. Очевидно, что в этом простейшем для анализа случае внешние ресурсы процесса безграничны, поэтому на данный процесс не влияют и их можно не принимать в расчет. В данном случае процесс ограничивает внутренний ресурс - скорость деления клеток микроорганизмов. В условиях постоянной температуры его также можно не учитывать, но при изменении температуры сразу же возникает температурный ресурс, который может быть как внешним, так и внутренним, если процесс сопровождается выделением тепла.
2. Если в предыдущем примере ограничить объем инкубатора, то в начале некоторое время процесс будет идти точно так, как в примере 1, но затем появляется и начинает влиять все сильнее ресурс ограниченного пространства. В конечном итоге он приведет к самоуничтожению культуры микроорганизмов.
3. При наличии ограниченного ресурса питания, удаления продуктов жизнедеятельности и т.п., мы придем к тому же неутешительному выводу.
Из этих примеров видно, что любой процесс определяется не изначально заданной закономерностью и стартовыми условиями (по-видимому, это представление сложилось под влиянием механики с ее строгим детерминизмом), а ресурсами, которыми располагает данный процесс в данный момент времени.
Любой процесс развивается на основе сиюминутного значения функции, например, закон радиоактивного распада получается в процессе распада только на основе того, что каждое ядро имеет определенную вероятность распада. Никто не будет сомневаться в том, что умудрись мы в какой-то момент изменить вероятность распада, и именно с этого момента процесс пойдет по-другому. В этом смысле предлагаемые ниже новые исчисления имеют не формально-математическую, а физическую основу, подсказывая новое значение функции на основе предыдущего ее значения. Это дает возможность значительно усовершенствовать математическое моделирование процессов, позволяя вносить коррективы в изменения функции по ее ходу, а не в исходную систему уравнений, при этом можно не знать граничных условий. Таким образом, новые исчисления позволяют так же гибко управлять изменением функции, как внешние условия управляют изменением самого изучаемого процесса. Прикладной науке нужны математические методы, чутко реагирующие на изменение ситуации, как это делает мозг живых существ. Мы никогда не создадим искусственный разум на основе каких-либо законов, которые априори предполагают жесткий детерминизм и исключают любую инициативу и непредсказуемое поведение.
3. Определение новых исчислений аналогичных дифференциальному и интегральному (D-исчисления)
Автор надеется, что изложенные ниже принципы новых исчислений окажут большую помощь ученым, занимающимся прикладными исследованиями, а для любителей математики здесь необъятное поле деятельности.
В известном дифференциальном исчислении производной функции:
(3.1)
в точке x называют предел отношения приращения функции к приращению аргумента, при стремлении приращения аргумента к нулю:
(3.2).
Условно назовем дифференциальное исчисление, основанное на этом определении производной и соответствующее интегральное исчисление d-исчислением.
Обобщим определение (3.2), приняв значение 
x
конечным, тогда из (3.2):
(3.3).
Для дальнейшего, удобнее переписать (3.3) в виде:
(3.4),
откуда, учитывая (3.1) и обозначив 
:
(3.5).
Продолжим обобщение, заметив, что при 
конечном, 
также конечно (для большинства функций),
поэтому определим множество производных функции 
так:
(3.6).
На основании обобщенного определения производной функции (3.6) можно
построить множество 
-исчислений
(назовем их также дифференциальными и интегральными за неимением другого
термина). d-исчисление будет одним из частных случаев при 
и 
.
Выделим во множестве -исчислений подмножество при 
, которое назовем D-исчислениями.
При этом необходимо учесть, что в реальных прикладных задачах за единицу можно
принимать любое изменение аргумента, поскольку единицы изменения аргумента в
прикладных задачах условны (см. примеры практического приложения D-исчисления).
Таким образом, D-производная функции 
определена нами выражением:
(3.7),
т.е. она определяется произвольной функцией от последующих и предыдущих
значений функции ,
при изменении аргумента на единицу (условную). Из (3.7) найдем 
:
(3.8).
Положим: 
(3.9),
где U и V - некоторые функции от x.
Подставив (3.9) и (3.8) в (3.7), найдем:
(3.10).
Мы получили основное выражение для нахождения любой производной из
множества D, структура которого сохранится и при 
.
Для сложной функции 
(функция от функции), из (3.10) получим:
(3.11).
Установим связь между производными функции внутри D-исчислений.
Для конкретного исчисления 
из (3.7) найдем:
(3.12).
Для исчисления 
из
(3.8) найдем:
(3.13).
Подставив (3.13) в (3.12), получим:
(3.14).
Выражение (3.14) устанавливает искомую связь.
Интересно также установить связь между D-исчислениями и известным d-исчислением.
Положим: 
(3.15), откуда: 
(3.16).
Положим: 
(3.17), откуда: 
(3.18).
Из равенства левых частей (3.16) и (3.18) имеем:
(3.19),
откуда можно выразить 
через 
или наоборот. Подставив (3.16) в (3.17) и
(3.18) в (3.15), найдем связь между d и D-исчислением в явном
виде:
(3.20),
(3.21).
Поскольку D-производные функций заданных, например, в точках, существуют, а d-производные нет, связь между d и D-исчислением для таких функций не раскрывается в явном виде выражениями (3.20) и (3.21), что вполне естественно.
4. D-дифференциальное исчисление
Для некоторых (взятых в качестве примера) D-исчислений в таблице
приведены правила дифференцирования, которые получаются из (3.10) и (3.11). Для
примера выбраны простейшие функции , а название конкретных D-исчислений
условно.
Таблица (4.1) D-производных.
Определение некоторых конкретных исчислений
|
Вид D-исчисления |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значение D-производной
функции |
|||
|
Тип |
|
|
|
|
|
0 |
|
|
|
|
2a |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
Тип |
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
Тип |
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
Тип |
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
Тип |
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
Тип |
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
Перевод
|
|||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
функция
от функции
в 
: 
Чтобы было понятнее, как заполняются ячейки таблицы, рассмотрим конкретный пример O-дифференцирования функции
(4.1),
где U и V
некоторые функции от 
.
Очевидно, что предыдущий член этой функции будет
(4.2).
По определению, 
(4.3).
Исходя из этого определения
, 
(4.4).
Подставив (4.1), (4.2) и (4.4) в (4.3), найдем значение O-производной функции (4.1):
(4.5),
которое соответствует значению, приведенному в таблице (4.1) (второй тип функции, третья строка).
В последнем разделе таблицы (4.1) приведены формулы перевода любого из
рассматриваемых D-исчислений в -исчисление, которые непосредственно
получаются из определения конкретного D-исчисления
и -исчисления,
например:
(4.6),
(4.7),
потенцируем (4.7), чтобы получить выражение для 
, которое подставим в (4.6) и
получим формулу перевода 
-исчисления в -исчисление:
(4.8).
Формула (4.8) соответствует последней ячейке таблицы (4.1).
Таблицу D-производных элементарных функций легко составить из
выражения (3.7) или, зная 
-производную - из (3.14). Например, D-производные
функции 
таковы:
, 
, 
, 
, 
, 
и т.д.
Дифференцировать функцию можно как непосредственно, так и пользуясь
правилами таблицы (4.1), например, функцию 
можно представить как отношение двух
функций: 
и 
. В обоих случаях получим
(для O-исчисления) 
.
Частные производные в любом D-исчислении определяются
так же, как и в d-исчислении, например, если
имеется функция нескольких переменных 
:
(4.9),
то частные производные в O-исчислении будут такими:
, 
, 
,
т.е. производится дифференцирование по одной переменной при постоянных значениях других переменных.
D-производные высших порядков получаются
дифференцированием производной более низкого порядка, например -производные
последовательно повышающегося порядка от функции 
будут такими: 
, 
, … 
.
D-производные тригонометрических функций
отличаются от остальных тем, что единицей изменения аргумента будет 
радиан, например:
(4.10),
тогда 
(4.11).
O-производная функции (4.10) будет:
(4.12),
а -производная:
(4.13).
Выражение (4.13) можно получить и из (4.12) воспользовавшись формулой
перевода O-исчисления в -исчисление из таблицы 4.1.
Правило дифференцирования универсально для любой функции – уменьшаем
аргумент функции на единицу (или на для тригонометрических функций) и записываем
соотношение между 
и
в соответствии
с определением конкретного исчисления.
Первообразную функцию для данной функции определим аналогично тому, как это делается
в d-исчислении, т.е. это такая функция 
D-производная от которой равна 
, соответствующий,
например, 
-интеграл:
(5.1).
В правой части (5.1) постоянная С присутствует в -исчислении. В других
исчислениях в правой части постоянная может отсутствовать, поэтому D-интеграл
можно определить так:
(5.2),
или, учитывая (3.8):
(5.3),
где А - постоянный множитель.
Выражение (5.3) нельзя трактовать, как неопределенный D-интеграл,
т.к., например, в -исчислении
постоянная С в подинтегральном выражении исчезнет, а в правой части
останется. Для таких исчислений D-интеграл будет неопределен тогда, как
например, S-интеграл будет определен, поскольку постоянные С и А
в подинтегральном выражении сохраняются при дифференцировании первообразной.
Трудности известного d-интегрирования сохраняются и в D-интегрировании, поскольку D-интеграл определяется так же не конструктивно, как и d-интеграл.
Рассмотрим любой неопределенный 
- интеграл, например:
(4.4) или 
(5.5).
Мы видим интересную особенность, заключающуюся в том, что в отличие от
множества первообразных функции 
в d-исчислении, получающихся путем
параллельного переноса вдоль оси y, в -исчислении множество первообразных данной
функции получается путем растяжения (сжатия) вдоль оси y.
Правила интегрирования для каждого D-исчисления так же различны,
как и правила дифференцирования, отраженные в таблице (4.1). Так, например,
постоянный множитель k выносится за знак D-интеграла 
так:
, 
, 
, 
, 
,
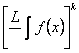(5.6).
Некоторые неопределенные интегралы приведены ниже. Наиболее простой прием «интегрирования» состоит в дифференцировании выражения, которое вам представляется полезным. Полученное выражение является подинтегральным выражением, т.е.
(5.7).
1. 
верен
при 
n- и также не целом n., 
2. 
3. 
4. 
5. 
, 
6. 
Если известно значение интеграла в каком-либо исчислении, то его легко перевести в любое другое исчисление, пользуясь формулами перевода таблицы (4.1). Например, формулу (5.5) с учетом (5.7) и формул перевода из одного исчисления в другое по таблице (4.1) можно привести к интегралу №2 (без постоянного множителя для простоты).
Правила интегрирования легко сформулировать, анализируя правила дифференцирования из таблицы (4.1), принимая во внимание определение интеграла (5.7).
1. - или
S-интеграл суммы (разности) равен сумме
(разности) интегралов отдельных членов.
2. O- или P-интеграл произведения равен произведению интегралов отдельных членов.
3. L-интеграл суммы отдельных членов равен произведению интегралов этих членов.
4. L-интеграл разности отдельных членов равен отношению интегралов этих членов.
5. 
-интеграл
произведения равен произведению обратных величин интегралов отдельных членов.
6. Правила интегрирования для более сложных случаев, когда интегрируется функция в показателе степени другой функции или интегрируется функция от функции, непосредственно следуют из таблицы (4.1) в которой тип функции является результатом интегрирования, а конкретная D-производная является подынтегральным выражением.
Аналогичным образом можно ввести понятие D-дифференциальных уравнений, а также все то, чем располагает аппарат современного дифференциального и интегрального исчисления. Конечно, это огромный труд, но учитывая вышеизложенное, как говорится, дело техники, поскольку принцип ясен.
6. D-дифференциальные уравнения
D-дифференциальные уравнения вводятся аналогично известным d-уравнениям. Эти уравнения содержат неизвестные функции, независимые переменные и производные неизвестных функций (или их дифференциалы) (пример 1). Основное отличие D-дифференциальных уравнений состоит в том, что в них могут содержаться производные и дифференциалы любого из D-исчислений или даже их смесь в одном уравнении (пример 1). Если неизвестные функции зависят только от одной независимой переменной, то D-дифференциальное уравнение будет называться обыкновенным (пример 1). Если независимых переменных несколько, то это уравнение с частными производными (пример 2). Порядком дифференциального уравнения называется наивысший из порядков производных или дифференциалов, входящих в уравнение (пример 3). Автор считает допустимым отнести к D-дифференциальным уравнениям также и уравнения, содержащие интегралы (пример 4).
Пример 1. 
Пример 2. 
Пример 3. 
- уравнение второго
порядка.
Пример 4. 
Приемы решения D-дифференциальных уравнений аналогичны известным приемам в d-исчислении. Отличие состоит в том, что всегда можно упростить решение выбором наиболее удачного исчисления для данного случая.
Часто могут встречаться D-дифференциальные уравнения не относящиеся к какому-либо из рассмотренных ранее D-исчислений. В них связь между текущим и предыдущим значением функции достаточно сложна. Приведем примеры интегрирования двух подобных D-дифференциальных уравнений.
Пример 5. 
, где R – постоянная величина.
Интеграл этого уравнения равен:
(6.1),
где 
- любая постоянная. Действительно,
из (6.1):
(6.2),
откуда:
(6.3).
Предыдущее значение функции:
(6.4),
откуда:
(6.5).
Приравнивая (6.3) и (6.5), найдем:
(6.6),
которое совпадает с данным уравнением примера 5.
Проверка.
Таблица 6.1.
|
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
Данные в таблице 6.1 соответствуют уравнениям (6.1) и (6.6).
Пример 6. Более сложный вариант уравнения (6.6):
(6.7).
Интеграл первого слагаемого в (6.7) будет равен:
(6.8).
Действительно, 
, откуда 
. Интеграл второго
слагаемого в (6.7) будет равен:
(6.9).
Действительно, 
, откуда 
. Складывая (6.8) и (6.9),
окончательно найдем:
(6.10).
Из приведенных примеров видно, что к D-дифференциальным уравнениям относятся любые соотношения в явном или неявном виде связывающие два значения функции. При прогнозировании мы фактически всегда ищем решение D-дифференциального уравнения.
7. Примеры применения новых исчислений
Рассмотрим некоторые примеры практического приложения D-исчислений.
Задача о радиоактивном распаде.
Известно, что масса M радиоактивного вещества уменьшается вдвое
через промежуток времени 
- времени полураспада, т.е.:
(7.1) или 
(7.2).
Интегрируя (7.2), получим:
(7.3).
За единицу масштаба времени мы выбрали 
. Для того чтобы получить зависимость от 
, нужно привести к выбранному
масштабу, т.е.:
(7.4).
Подставив (7.4) в (7.3), получим:
(7.5).
При 
, следовательно,
окончательно будем иметь:
(7.6),
что и является уравнением радиоактивного распада.
Рассмотрим еще одну задачу, приводящую к -дифференциальному уравнению. Предположим,
что мы закрываем некую поверхность слоями непрозрачных хаотически расположенных
частиц с коэффициентом заполнения 
в каждом слое. Требуется найти закрытую
площадь y, как функцию числа слоев x. Очевидно, что:
(7.7).
Откуда легко найти -дифференциальное уравнение, перенеся 
в левую часть (7.7):
(7.8).
Интегрируя (7.8), получим:
(7.9).
Проверим (7.9), -дифференцируя:
(7.10)
(7.11),
(7.12).
Разделив обе части (7.12) на , получим:
(7.13).
Из (7.11): 
(7.14)
Подставив (7.14) в (7.13), найдем: 
, т.е. (7.8).
Посмотрим, как в -исчислении будет выглядеть задача
определения вида функции, вторые разности которой постоянны. Как известно - это
парабола. Очевидно, что вторая -производная при этом постоянна:
(7.15).
Интегрируем (7.15) один раз:
(7.16).
Интегрируем (7.16) еще раз:
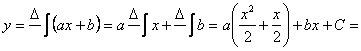
(7.17).
Проверим (7.17):
(7.18).
(7.19),
(7.20).