В этой главе мы проанализируем основы современной квантовой механики. Она фактически не корпускулярная, а волновая. Будет показано, что хотя она и оперирует массой и энергией частицы, фактически свойства частиц в ней игнорируются в угоду волновым свойствам. В этом случае легко получить квантовые состояния системы, стоит лишь легально или нелегально представить частицу в виде стоячей волны. При этом находят объяснение некоторые экспериментальные факты, не объяснимые классической механикой. Одновременно возникают не имеющие физического смысла результаты. Например, любая связанная частица в волновой квантовой механике оказывается разделенной на отдельные кусочки и размазанной по пространству, т.к. частицы нет там, где волновая функция равна нулю (в узлах стоячей волны) и размазана в пространстве, где волновая функция отлична от нуля (в пучностях стоячей волны). Сама частица, связанная со стоячей волной, тоже неподвижна, хотя может находиться в силовом поле и должна двигаться. Но тогда стоячая волна превращается в бегущую волну и квантованность уровней энергии сразу пропадает. Кроме того, постоянное возникновение бесконечностей при расчетах, от которых приходится правдами и неправдами избавляться, буквально замучили волновую квантовую механику.
Новая физика волновые свойства частиц связывает с движением их по винтовой линии. Причиной такой траектории является возникновение гравидинамического поля при движении гравитационных зарядов. На основании этого новую физику можно назвать корпускулярной квантовой механикой в отличие от официальной волновой квантовой механики. Таким образом, сейчас в нашем распоряжении будут волновая квантовая механика, классическая механика и корпускулярная квантовая механика. Далее мы сравним эти три подхода в указанной последовательности к физическим явлениям и увидим, какой из них не конфликтует со здравым физическим смыслом.
Комментарии автора к главе 3:
1. Классическая и квантовая физика.
Ознакомление со свойствами микромира вызвало большие сомнения в применимости законов классической физики в результате чего появилась квантовая физика. Ученых, ностальгирующих до сих пор по «чистой» классической физике легко понять – замена детерминистского описания мира вероятностным описанием вызывает внутренний протест против «божественного провидения». Но и они должны понять, что классическая физика безвозвратно канула в Лету и всякие попытки реанимировать ее в первозданном виде бесполезны. Единственный путь вернуть в физику здравый смысл – радикально «поправить» классическую физику, по существу, разрабатывать неоклассическую физику, основанную на проверенном веками принципе детерминизма.
Квантовая физика базируется на вероятностном описании мира. Мы, конечно, можем пользоваться теорией вероятности для статистического описания сложных событий, но предсказать, например, какой стороной упадет брошенная монета невозможно с вероятностью больше 0,5. Теперь бросим эту монету и с вероятностью равной единице она упадет той стороной, которую видим после броска. Таким образом, после того, как событие произошло, его вероятность равна единице. Поэтому все наши размышления и расчеты до события являются фикцией. Такой же фикцией является и вероятностное описание мира, т.е. квантовая волновая физика является лженаукой, приводящей нас в заблуждение. В любой момент времени любая частица микромира находится в строго определенном месте и имеет определенную скорость. Что будет с ней через мгновение официальная физика в точности не знает, а ее вероятностные предположения ничего не стоят, т.к. с вероятностью равной единице не совпадут с тем, что произойдет через это мгновение.
2. У квантовой механики нет фундамента.
Создатели квантовой механики полагали, что ее фундаментом может служить образование стоячей волны в микросистемах, связанной с волновыми свойствами частиц. Тогда целочисленные значения квантовых состояний системы легко объясняются, но здесь возникает принципиальная трудность, которая не позволяет реализовать эту идею. Напомню необходимые условия возникновения стоячей волны. Стоячие волны являются частным случаем интерференции в результате наложения двух волн, распространяющихся в противоположных направлениях с одинаковой частотой, поляризацией (для поперечных волн) и одинаковой амплитудой в соответствующей координате. В стоячей волне отсутствует перенос энергии, т.к. прямая и обратная волна переносят энергию в равных количествах. При нарушении любого из перечисленных условий образование стоячей волны невозможно. Тем не менее, официальная физика применяет уравнение Шредингера во всех случаях, когда образование стоячей волны невозможно. Поскольку в реальных микросистемах нигде нет вертикальных стенок потенциальной ямы, то отраженная волна не может распространяться в направлении падающей. Например, в атоме сферически симметричное электростатическое поле ядра нигде не имеет вертикальных «стенок», при рассмотрении «туннельного» эффекта отраженная волна не может иметь амплитуду падающей, поэтому образование стоячей волны невозможно. Эту принципиальную трудность квантовой механики ее создатели прекрасно сознавали, поэтому рассматривали исключительно придуманные нереальные модельные системы с вертикальными стенками потенциальной ямы, а выводы такого рассмотрения переносили на реальные системы. Это не научный метод исследования. Зачем создатели квантовой механики (которые считаются великими учеными) пренебрегали научной добросовестностью ради достижения своей цели? Ответа нет. Возникает единственное подозрение, что человечество периодически поражается глобальным помрачением сознания по неизвестным причинам (почти одновременно с квантовой механикой возникли две мировые войны, революция, гражданская война и теория относительности).
3.1. Движение свободной частицы и соотношения неопределенностей Гейзенберга
Волновая квантовая механика. Неопределенности Гейзенберга:
Pxx
h
(3.1.1)
можно для рассматриваемой одномерной задачи переписать в виде:
Pxh
(3.1.2).
Если мы точно
узнаем значение импульса частицы (P=0), то в
соответствии с (3.1.2) x=
и частица с равной вероятностью находится в любом месте бесконечной оси x. Хотя вероятность встретить частицу на всей бесконечной
оси x равна единице (частица есть, но размазана
по всей оси), вероятность встретить ее в любой точке xi
равна нулю (1/=0),
т.е. в любой точке оси частицы нет. Это неразрешимое в рамках здравого смысла
противоречие. Если учесть, что в рассматриваемом случае проекция импульса на
ось y и ось z
равна нулю, то и Py и Pz
также равны нулю и тогда частица размазана по всему бесконечному пространству.
Фактически, соотношения неопределенностей Гейзенберга запрещают любое взаимодействие микрочастиц. Рассмотрим, например, столкновение частиц во встречных пучках. Очевидно, что столкновение двух частиц происходит в определенной точке пространства, но тогда импульсы (и энергия) этих частиц бесконечно большие и не было смысла их разгонять. Если «сталкиваются» две частицы с определенными импульсами, то вероятность их встречи равна нулю, т.к. их с равной вероятностью можно найти во всем бесконечном пространстве. То же относится и к обменному взаимодействию посредством виртуальных частиц. Таким образом, соотношения Гейзенберга, объясняя возникновение виртуальных частиц, одновременно лишают их способности каким-либо образом проявить себя, что возможно только через взаимодействия.
Соотношения неопределенностей Гейзенберга противоречат теории относительности, что подтверждается следующей цитатой (Физическая энциклопедия под редакцией А.М. Прохорова, т.3, М, 1992, стр. 494): «Основное понятие теории относительности – событие, под которым понимается нечто происходящее в данный момент времени в данной точке пространства (например, вспышка света или совпадение стрелки прибора с делением шкалы). Реальные события имеют конечную протяженность в пространстве и времени, поэтому понятие события в теории относительности является идеализацией. Опыт показывает, что применимость этой идеализации очень высока, вплоть до расстояний ~10-16 см и времен ~10-26 сек». Очевидно, что этот же опыт отвергает соотношения неопределенностей.
Классическая механика. Здесь противоречий не возникает. Зная начальную скорость и направление движения, мы можем точно рассчитать траекторию движения частицы и всегда укажем, когда и где ее встречать.
Корпускулярная квантовая механика. Физический смысл неопределенностей Гейзенберга был раскрыт в предыдущей главе. Если мы точно знаем проекцию импульса частицы на ось x, вдоль которой она движется (фигура 3.1.1), то неопределенность положения самой частицы:
 |
(3.1.3)
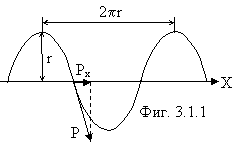равна длине волны де Бройля или длине окружности поперечного сечения винтовой траектории.
Тангенциальная и поступательная скорость частицы на винтовой траектории равны, поэтому проекция импульса на направление движения всегда постоянна и равна:
(3.1.4).
С другой стороны, момент импульса частицы:
(3.1.5).
Учитывая, что 
и подставляя (3.1.3) и (3.1.4) в
(3.1.5), найдем:
(3.1.6).
Очевидно, чтобы избавиться от неопределенности в положении частицы в пространстве, надо указать не только начальную скорость и направление движения, но и начальную фазу движения, т.е. начальное положение частицы на винтовой траектории. Далее, как и в классической механике, мы можем рассчитать траекторию движения частицы и с вероятностью равной единице встретить ее в любой желаемой точке этой траектории.
Комментарии автора к главе 3.1.
Примеры противоречий с соотношениями неопределенности:
1. Атом водорода.
Атом
водорода стабилен, поэтому за любой промежуток времени t
изменение энергии этого атома равно нулю, поэтому Et=0.
Радиус атома водорода равен радиусу орбиты Бора, поэтому x=r=0.
Импульс электрона на орбите Бора не меняется P=mV=0, поэтому Px=0.
Сторонники скорости – вектора это соотношение могут рассматривать после каждого
полного оборота.
2. Ионизация атомов.
Воспользуемся
соотношением неопределенности в виде Px
h/2
(1) в применении к любому
электрону атома, где P=P – импульс электрона, а x=r0 – классический радиус электрона. Энергия
электрона E=P2/me (2) где me
– масса электрона. Из (1): P2=(h/2r0)2 (3). Подставив (3) в (2) и
табличные значения постоянных, найдем, что соотношения неопределенностей заставляют
любой электрон атома иметь энергию 96 Мэв. Очевидно, что эта энергия превышает
энергию ионизации внутренних электронов даже тяжелых атомов, поэтому любые
атомы мгновенно растеряют все электроны, оставив голые ядра. Ортодоксы здесь
попадают в затруднительное положение и, чтобы выкрутиться, обвинят автора в
применении неверного размера электрона (с их точки зрения). Но чтобы наружные
электроны не терялись атомом, их размер должен быть в несколько тысяч раз
больше, что невероятно. Официальные представления исходят из точечного размера
электрона или планковского размера. Тогда энергия электронов получится вообще
умопомрачительной. Кстати, соотношения неопределенностей перечеркивают все
спекуляции струнных теорий, т.к. размеры «струн» предполагают равными планковской
длине 10-33 см. В этом случае энергия «струн» в 1040 раз
должна превышать энергию электронов. Полный бред!
3. Соотношения неопределенностей приводят к неразрешимым противоречиям.
Запишем два известных выражения соотношения неопределенностей:
Eth/2 (1) и Pxh/2 (2). Левые части (1) и
(2) относятся к одному и тому же выражению, следовательно, равны между собой.
Приравняем: Et=Px (3).
Преобразуем (3): E/P=x/t (4).
Расшифруем значения физических величин в (4): E=mc2
– изменение полной энергии частицы, P=mV
– изменение импульса частицы, x/t=V
– изменение скорости частицы. Подставим все в (4): mc2/mV=V
или c=V. Таким образом,
совместное решение соотношений неопределенности дает очевидный глупый
результат: все микрочастицы в любых условиях квантовой механики должны
двигаться со скоростью света. Этот результат противоречит ортодоксальным
представлениям теории относительности и опытным данным, поскольку скорость
микрочастицы может быть как угодно малой. Отсюда делаем вывод, что квантовая
механика – ложная теория в самой своей основе.
4. Скрытая математическая ошибка в соотношениях неопределенности.
Запишем
соотношение неопределенности в виде: Px=h/2
(1). Вычислим P=P2-P1= h/2 (1/x2-1/x1)= h/2 (-x/x2x1) (2).
Откуда: h/2 = -Px2x1/x
(3). Сравнивая (3) и (1) можно сделать выводы: 1. Левая часть равенства (1)
всегда отрицательна, а правая положительная, что невозможно. 2. Приравнивая (1)
и (3), найдем: x=i(x2x1)^(1/2), т.е. x – всегда мнимое число
не имеющее физического смысла, поэтому не имеют смысла и соотношения
неопределенности, поскольку аналогичные процедуры с соотношением Et=h/2
приводят к точно таким же результатам.
3.2. Движение частицы на дне потенциальной ямы с плоским дном
Волновая квантовая механика. Для решения этой задачи используют стационарное уравнение Шредингера. При этом допускается, что потенциальная энергия от времени не зависит (стационарное движение). Здесь нужно несколько слов сказать о самом уравнении Шредингера. Строить огромный раздел науки, такой, как волновая квантовая механика, на основе одного лишь уравнения – рискованное занятие. Всегда можно показать, что любое уравнение физики или ошибочно или пределы его применения ограничены, оно не точно, значит тоже ошибочно. «Идеальных» уравнений не существует, поэтому мы вынуждены идеализировать саму природу, изобретая «идеальный газ», «точечные заряды», «свободные тела» и т.п. За любым уравнением стоят определенные физические представления и постулаты. Справедливость уравнения Шредингера подтверждают совпадением некоторых его решений с опытными данными. Очевидно, что такое совпадение подтверждает применимость, однако не доказывает правильность. Один и тот же результат часто можно получить из прямо противоположных представлений. А если при решении уравнения совпадают «нужные» результаты и отбрасываются «не нужные», то в итоге всегда можно получить то, что нужно.
Например, если кинетическую энергию частицы:
(3.2.1)
выразить через импульс частицы, то следует записать:
(3.2.2).
В уравнении Шредингера выражение (3.2.2) после умножения числителя и знаменателя на m записывают в виде:
(3.2.3).
При этом извращают физический смысл кинетической энергии на противоположный. Поскольку для свободной частицы P=const, то Ek по (3.2.3) обратно пропорциональна массе частицы. Для чего это делается? Чтобы не возиться с извлечением корня из суммы квадратов проекций импульса:
(3.2.4),
отпадает необходимость в физическом толковании двух значений корня. Если использовать (3.2.2), то скорость частицы является принципиальной помехой, т.к. в стоячей волне «частица» неподвижна.
Стационарное движение возможно только в двух случаях.
1. На круговой орбите. Для этого случая стационарное уравнение Шредингера не подходит, т.к. оно не учитывает энергию связи. Чтобы получить полную энергию, которая постоянна, надо учесть и энергию связи. Неизменной остается только алгебраическая сумма кинетической, потенциальной и энергии связи.
2. В потенциальной яме с плоским дном. В этом случае частица свободна и может изменить направление движения, только отражаясь от стенок ямы. При этом кинетическая энергия частицы не меняется и совпадает с полной энергией частицы, т.к. потенциальную энергию в рассматриваемой задаче можно приравнять нулю.
При решении принимают, что у стенок ямы волновая функция принимает нулевые значения. Физически это означает, что «прилепив» к частице волну, внутри ямы рассматривают только стоячие волны, т.е. на длине ямы должно укладываться целое число полуволн. Поэтому получаются только вполне определенные значения кинетической энергии, которыми может обладать волна-частица. Здесь сразу возникают два вопроса, на которые волновая квантовая механика не отвечает.
1. Откуда агент внешнего воздействия (фотон, атом или иная частица) могут знать о «разрешенных» энергетических уровнях, чтобы изменить кинетическую энергию частицы в яме на определенную величину. Если переданный импульс не будет соответствовать уровню энергии, то образование стоячей волны станет невозможным, и все уровни сразу пропадут.
2. Почему принимаются во внимание только стоячие волны, и игнорируется общий случай бегущей волны? Естественно, что при учете бегущих волн все выводы о квантовании энергии в потенциальной яме окажутся ошибочными.
Стоячие волны являются частным случаем интерференции в результате наложения двух волн, распространяющихся в противоположных направлениях с одинаковой частотой, поляризацией (для поперечных волн) и одинаковой амплитудой в соответствующей координате. В стоячей волне отсутствует перенос энергии, т.к. прямая и обратная волна переносят энергию в равных количествах. При нарушении любого из перечисленных условий образование стоячей волны невозможно.
В связи с этим возникают дополнительные вопросы.
1. Каков механизм интерференции частицы самой с собой?
2. Каким образом одна частица разделяется на несколько частей, каждая ее часть находится в пучностях стоячей волны и отсутствует в узлах?
Здесь нет смысла приводить решение уравнения Шредингера для каждой конкретной задачи, чтобы не ломать голову читателю. Желающие путешествовать в сложных математических лабиринтах решений могут обратиться к специальной литературе. Приведу готовый результат (например, Г.Е. Пустовалов. Атомная и ядерная физика. Изд. Московского университета, 1968, стр. 51):
(3.2.5),
где l – длина потенциальной ямы.
Классическая механика. Очищенный от квантовомеханических нагромождений физический смысл задачи о частице в потенциальной яме можно проиллюстрировать чисто классической моделью. Возьмем шнур массой m, закрепленный на концах и начнем возбуждать в нем поперечные колебания так, чтобы образовалась стоячая волна, например, из одной полуволны. Очевидно, что для этого потребуется затратить определенную энергию. Чтобы организовать стоячую волну из двух полуволн, надо добавить порцию энергии не какую попало, а определенной величины. В результате рассмотрения этой классической модели, мы получим точно такие же результаты, как и при решении уравнения Шредингера. Поэтому «чудесное» возникновение квантовых уровней энергии при движении частицы в ограниченной области является обманом – результатом квантовых добавок энергии для обеспечения образования стоячей волны.
Корпускулярная квантовая механика. Здесь придется рассмотреть совершенно абсурдную с точки зрения физического смысла модель, когда частица, отражаясь от стенок ямы, образует «стоячую волну» (фигура 3.2.1). Но эта ситуация не более абсурдна, чем нарезанная на кусочки частица, неподвижная с равномерно распределенными кусочками по дну потенциальной ямы.
 |
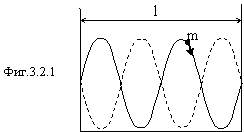Правовинтовая частица, двигаясь вдоль ямы, отражается от стенки и движется в обратном направлении уже в качестве левовинтовой частицы. Провозгласим абсурдное требование, чтобы внутри потенциальной ямы всегда возникала “стоячая волна”, т.е. на длине ямы послушная частица укладывала целое число полувитков своей винтовой траектории. Очевидно, что минимальная энергия частицы будет в том случае, если в яме укладывается только полвитка винтовой траектории. При еще меньшей энергии длина волны де Бройля (шаг винтовой траектории) становится такой, что полволны уже не укладываются в размеры ямы и образование “стоячей волны” невозможно. Относительно этого официальная физика спекулирует вокруг “нулевых колебаний”, виртуальных частиц вакуума и прочей ерунды.
Момент импульса частицы на витках винтовой траектории:
(3.2.6).
Длина волны де Бройля равна длине окружности поперечного сечения винтовой траектории:
(3.2.7).
Подставляя (3.2.6) и (3.2.7) в (3.2.1), найдем:
(3.2.8).
Условие “стоячей волны”:
(3.2.9),
где n – целое число (n=1,2,3…), подставим в (3.2.8) и получим (3.2.5). Таким образом, мы получили полное совпадение с официальным квантовомеханическим расчетом. При этом мы совершенно не пользовались уравнением Шредингера. Мало того, при этом использован примитивный математический аппарат, исключающий возможность оспаривания полученного результата (сравните с официальными манипуляциями при выводе (3.2.5), обратившись к указанной литературе). Поскольку ни официальное решение этой задачи, ни пример решения, предлагаемого новой физикой, не имеют физического смысла, единственный вывод, который можно сделать – это сомнение в правильности уравнения Шредингера.
3.3. Движение частицы в потенциальной яме с потерей энергии
Волновая квантовая механика. Для указанной задачи стационарное уравнение Шредингера не подходит. Потенциальная энергия частицы постоянно меняется во времени, а решение общего уравнения Шредингера настолько сложно, что не имеет смысла с ним возиться, когда можно просто получить уровни энергии для этой задачи с помощью классической или корпускулярной квантовой механики без использования волновой квантовой механики.
Классическая механика. На фигуре 3.3.1 представлена потенциальная яма в виде цилиндра высотой h0 с плоским дном.
 |
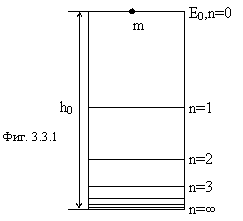Возьмем шарик массой m и отпустим его с высоты h0 без начальной скорости. Если потери энергии отсутствуют, то шарик будет бесконечно прыгать, каждый раз возвращаясь в исходную точку. В этом случае полная энергия шарика останется всегда численно равной E0, переходя из потенциальной в кинетическую и обратно. Очевидно, чтобы достичь дна потенциальной ямы, шарик должен растерять энергию:
(3.3.1),
где g – ускорение свободного падения.
Предположим, что при каждом ударе о дно цилиндра шарик потеряет определенную долю K от исходной энергии. Тогда:
(3.3.2).
При i-том отскоке:
(3.3.3),
где n=0,1,2,3,… - число отскоков. Из (3.3.3) видно, что при K=0 (идеально упругий шарик и цилиндр), шарик будет прыгать вечно, а при K=1 (пластилиновый шарик) он прилипнет к дну цилиндра и E0 сразу превратится в тепло. При K=0,5 уровни энергии изображены на фигуре 3.3.1.
Мы видим, что число энергетических уровней бесконечно, и они сгущаются вблизи основного состояния. Эта картина полностью соответствует атому водорода новой физики и прямо противоположна ортодоксальным представлениям. Полная энергия шарика в этой задаче равна нулю и является алгебраической суммой потенциальной, кинетической энергии и энергии связи: Еполн=Епот+Екин+Есв=0. Все энергетические уровни официальной физики расположены «вверх ногами» из-за непонимания разницы между энергией уровня и энергией связи. Для нашей задачи:
(3.3.4).
Формула для энергетических уровней атома водорода по теории Бора, волновой механике и корпускулярной механике имеет один и тот же вид:
(3.3.5),
где Ei – энергия уровня, которая откладывается от основного состояния, E0 – максимально возможная энергия уровня. Очевидно, что энергия связи электрона с ядром:
(3.3.6).
При n
, EсвE0.
Корпускулярная квантовая механика. Здесь рассуждения такие же, как и в предыдущем пункте. Только вместо шарика рассматриваем электрон с начальной потенциальной энергией E0. Энергия после первого отскока от дна потенциальной ямы будет:
(3.3.7),
а после i-того отскока:
(3.3.8).
В теории атома новой физики и в теории образования Солнечной системы показано, что радиальная скорость тела в новом квантовом состоянии в целое число раз меньше начальной скорости:
(3.3.9).
Подставив (3.3.9) в (3.3.8), после некоторых преобразований получим:
(3.3.10).
Подставив (3.3.10) в (3.3.8), найдем:
(3.3.11).
Энергия связи электрона будет:
(3.3.12).
При каждом отскоке от дна потенциальной ямы электрон излучает фотоны за счет тормозного излучения.
Волновая квантовая механика. При рассмотрении туннельного эффекта официальная физика вынуждена допускать коэффициент отражения от стенки потенциальной ямы (потенциального барьера) меньше единицы, чтобы частица могла проникнуть внутрь барьера. При этом сразу нарушается главное условие образования стоячей волны, и квантовые уровни исчезают, превращаясь в непрерывный спектр. При этом возникает следующая дилемма. Если мы хотим сохранить квантованность, нам придется отказаться от туннельного эффекта, а если хотим сохранить туннельный эффект – придется отказаться от набора квантовых уровней энергии. Для дальнейшего придется прикинуться ничего не знающим об этом противоречии.
Для решения этой задачи используют также стационарное уравнение Шредингера, хотя надо использовать временное уравнение. При этом мы будем иметь дело с бегущей волной, т.к. стоячая волна не обладает свойством проникать в какие-либо препятствия. При рассмотрении туннельного эффекта вводят коэффициент проницаемости барьера:
(3.4.1),
где N – число частиц прошедших через барьер, N0 – число частиц падающих на барьер. Поскольку уравнение Шредингера не дает никаких указаний на отличие частиц друг от друга, то, очевидно, что если одна частица отразилась от барьера, то отразятся и все остальные частицы. Если частица прошла через барьер, то проникнут и все остальные. Чтобы выйти из этого затруднения, придется каждую падающую на барьер частицу представлять волной, а не частицей. Только волна способна частично отразиться от барьера, частично проникнуть в барьер, частично поглотиться в нем и выйти на другую сторону барьера. В результате мы получаем невероятное состояние для частицы. Часть ее отражается, часть поглощается в барьере, а часть проходит через барьер. Поэтому официальная физика путем манипуляций, не имеющих физического смысла, получает формулу для коэффициента проницаемости потенциального барьера, также лишенную физического смысла (см., например, Г.Е. Пустовалов. Атомная и ядерная физика. Изд. Московского университета, 1968, стр. 58):
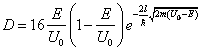(3.4.2),
где E – общая энергия частицы массой m, проходящей через потенциальный барьер шириной l для преодоления которого необходима энергия U0. Предполагается, что E<U0 и классическая частица не преодолеет барьер. Но, положив E=U0 (классическая частица преодолеет барьер), из (3.4.2) видно, что при этом D=0, т.е. «квантовая» частица не способна преодолеть барьер. Если E>U0, то (3.4.2) дает такой результат, которому невозможно придать разумный физический смысл. D становится отрицательным, а в экспоненте появляется мнимая величина. Ортодоксы предпочитают спрятать этот нонсенс, обозначив:
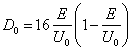(3.4.3)
и
считая D0 
1. В итоге этого обмана получают вполне
благопристойное выражение:
(3.4.4).
Классическая механика. Для преодоления барьера «классическим» способом официальная физика привлекает соотношение неопределенности Гейзенберга, по которому нельзя одновременно точно определить кинетическую и потенциальную энергию частицы. Поэтому недостающую потенциальную энергию официальная физика «занимает» у кинетической энергии, чтобы не нарушать фундаментальный закон сохранения энергии. Очевидно, что без привлечения дополнительной энергии туннельный эффект невозможен, т.к. он противоречил бы закону сохранения энергии. Поэтому, если классической частице не хватает немного энергии, то ее можно «добавить». Например, если кинетическая энергия катящегося шарика меньше той потенциальной энергии, которую надо сообщить, чтобы преодолеть барьер, нужно учесть, что кроме перемещения с определенной скоростью шарик еще и вращается при качении, поэтому полная его энергия больше кинетической. Микрочастицам проще – они всегда могут получить дополнительную энергию от энергичных частиц «хвоста» больцмановского распределения.
 |
Корпускулярная квантовая механика. Здесь мы будем нелегально протаскивать идею о том,
что кроме поступательной кинетической энергии частица обладает такой же
энергией и по виткам винтовой траектории, т.к. ее поступательная и
тангенциальная скорости равны. Легально эта идея будет сформулирована при
обсуждении 
-распада
ядер атомов. Рассмотрим фигуру 3.4.1, на которой изображен потенциальный барьер
и траектория движения частицы вблизи вершины барьера.
Коэффициент «проницаемости» барьера будет определяться формулой (3.4.1). Если на барьер падает множество частиц с разной фазой движения, то число падающих частиц пропорционально длине окружности поперечного сечения винтовой траектории (длине волны де Бройля):
(3.4.5),
а число частиц прошедших через барьер пропорционально части дуги винтовой траектории, торчащей над барьером:
(3.4.6),
где
- центральный
угол дуги, выраженный в радианах. Подставив (3.4.5) и (3.4.6) в (3.4.1),
получим:
(3.4.7).
Стрела h торчащего над потенциальной ямой сегмента определяется известным выражением (см., например, И.Н. Бронштейн, К.А. Семендяев. Справочник по математике. М.,1962, стр. 169):
(3.4.8).
Найдем из этого выражения
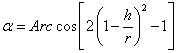(3.4.9).
Подставив (3.4.9) в (3.4.7), получим:
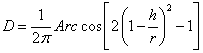(3.4.10).
Очевидно, что связь между 
и энергиями устанавливается
следующим соотношением:
(3.4.11).
Действительно, если h=2r (U0=0), то все частицы пройдут через барьер. Если h=r (U0=E), то половина частиц пройдет, а половина отразится от барьера. Если h=0 (U0=2E), то ни одна частица через барьер пройти не может. Подставив (3.4.11) в (3.4.10), найдем окончательно:
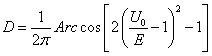(3.4.12).
 |
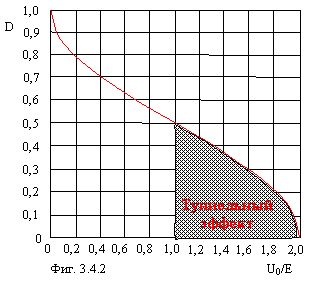График изменения D в зависимости от отношения U0/E представлен на фигуре 3.4.2.
Таким образом,
мы объяснили «туннельный» эффект в рамках новой физики. Оказывается, что
частица может преодолеть потенциальный барьер высота которого почти равна
двойной энергии поступательного движения частицы. При равенстве энергии частицы
и высоты барьера, его преодолевают 50% частиц, остальные отражаются. Если речь
идет об одной частице, то 50% соударений частицы с барьером приведут к ее отражению,
а 50% приведут к прохождению через барьер. Это справедливо, т.к. новая физика
отрицает образование стоячей волны до барьера, поэтому при каждом сближении
частицы с барьером, ее фаза движения на винтовой линии будет разной. Даже при
высоте барьера всего 10% от энергии частицы, почти 15% частиц отражаются от
него.
На основании полученных результатов этого раздела и раздела 2.1.2 можно сформулировать следующее очевидное правило: чем больше разница в количестве здравого физического смысла исходных представлений, тем сильнее различаются полученные результаты.
3.5. Линейный гармонический осциллятор
Волновая квантовая механика. В этой задаче официальная физика вновь разрезает осциллятор на отдельные куски в количестве n, расположенные по линии колебаний. В узлах стоячей волны осциллятора плотность вероятности нахождения частицы равна нулю. Конечное выражение для уровней энергии осциллятора (см., например, Р. Спроул. Современная физика. Изд. «Наука», М., 1974, стр. 164):
(3.5.1),
где
n=0,1,2,3…, 
- частота колебаний осциллятора в основном
состоянии, т.е. осциллятор может находиться только на более высоких
энергетических уровнях относительно основного состояния. При n
осциллятор должен получить бесконечно большую энергию, что лишено физического
смысла. Минимальная энергия осциллятора по официальным представлениям
составляет h/2.
Классическая механика. Излучение диполя достаточно хорошо проработано в классической физике. Диполь излучает в направлении перпендикулярном движению заряда и в том случае, если на концах диполя противоположные фазы колебаний. При одинаковых фазах излучения нет.
 |
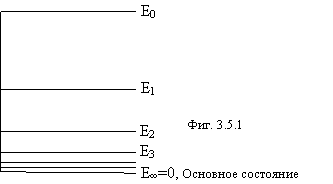Другой классической моделью осциллятора может служить маятник. Если он не теряет энергию (не «излучает»), то качается вечно. Если с каждым качанием будет терять порцию энергии, составляющую некоторую долю от исходной энергии, то его энергетические уровни расположатся в соответствии с фигурой 3.5.1. В процессе квантовой потери энергии частота колебаний маятника не меняется, амплитуда колебаний уменьшается, а теряемые порции энергии постепенно уменьшаются.
Корпускулярная квантовая механика. При гармоническом колебании заряженной частицы:
(3.5.2)
ее скорость:
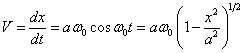(3.5.3).
При x=0:
(3.5.4),
где
- амплитуда, 
- циклическая частота. В
этом случае осциллятор обладает только кинетической энергией. При 
, V=0 и осциллятор обладает только потенциальной энергией.
Полная энергия осциллятора будет численно равна:
(3.5.5).
(3.5.4) подставим в (3.5.5):
(3.5.6).
Момент импульса электрона:
(3.5.7)
 |
подставим в (3.5.6):
(3.5.8).
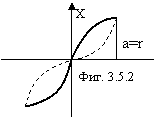
Движение осциллятора показано на фигуре 3.5.2.
Из фигуры видно, что амплитуда колебания осциллятора
равна радиусу винтовой линии. С учетом этого, и учитывая, что 
, а 
, выражение (3.5.8) примет вид:
(3.5.9).
При излучении осциллятора Vmax может уменьшаться только в целое число раз:
(3.5.10),
где n=1,2,3… (3.5.10) подставим в (3.5.6):
(3.5.11).
Из (3.5.11) видно, что при n=1
осциллятор будет иметь максимальную энергию 
, а при n
осциллятор теряет всю свою энергию и больше не излучает (находится в основном
состоянии). Этот факт можно интерпретировать двояко. Или электрон неподвижен,
или движется по круговой, а не эллиптической орбите, поэтому не излучает. В
последнем случае есть смысл Ei использовать для вычисления энергии связи электрона с
ядром:
(3.5.12).
При n максимальная энергия связи (основное состояние без излучения):
(3.5.13).
Энергию осциллятора h/2 ортодоксы считают
минимальной энергией «нулевых колебаний» (см. выражение 3.5.1). Новая физика
придерживается противоположного мнения, h/2 – максимально
возможная энергия осциллятора. Действительно, для атома водорода на орбите Бора
(основное состояние):
(3.5.14),
где
r0 –
радиус орбиты Бора. Учтем еще известные соотношения: 
, 
, 
и все подставим в (3.5.13):
(3.5.15).
Подставляя в (3.5.15) табличные значения, найдем:
2,1795×10-11
эрг = 13,60 эв (3.5.16),
что указывает на правильность представлений корпускулярной квантовой механики и ошибочность волновой квантовой механики. Уровни энергии по (3.5.11) показаны на фигуре 3.5.3.
 |
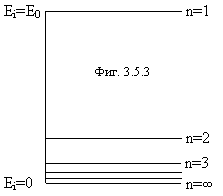Сравнивая формулы (3.5.1) и (3.5.11) мы видим, что энергетический
спектр осциллятора в волновой квантовой механике ограничен со стороны низких
энергий (n=0), но не ограничен со стороны высоких энергий
(разрешает так называемую «ультрафиолетовую катастрофу»). Энергетический спектр
осциллятора в корпускулярной квантовой механике, наоборот, не ограничен со
стороны низких энергий (n=), но ограничен значением h/2 со
стороны высоких энергий. Это полностью соответствует экспериментально изучаемым
энергетическим спектрам различных процессов, которые резко ограничены некоторым
максимальным значением энергии.