22. ПРИЧИНЫ КВАНТОВЫХ СОСТОЯНИЙ КОСМИЧЕСКИХ ТЕЛ
 |
Спутниковая система может быть образована вокруг центрального тела при захвате космических тел только с определенной длиной волны. Поэтому для макротел необходимо различать «длину волны» макротела, которая зависит от поступательной скорости на витках винтовой траектории и «амплитуду волны», которая зависит от тангенциальной скорости макротела на витках винтовой траектории. При одной и той же скорости поступательного движения Vf (одинаковой «длине волны»), тангенциальная скорость Vt должна определяться соотношением:
Vt=Vf∙n (22.1),
где n – целое число ![]() 1. Только при условии
(22.1) за время прохождения «длины волны» тело успеет совершить точно один
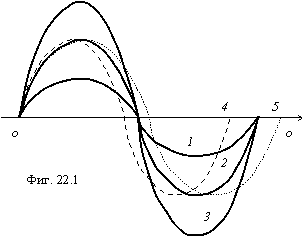
оборот по витку винтовой траектории. Это хорошо видно из фигуры 22.1, где в
масштабе изображены траектории движения космических тел вдоль оси O-O.
1. Только при условии
(22.1) за время прохождения «длины волны» тело успеет совершить точно один
оборот по витку винтовой траектории. Это хорошо видно из фигуры 22.1, где в
масштабе изображены траектории движения космических тел вдоль оси O-O.
Сплошной линией показаны траектории тел с одной длиной волны, но с разной амплитудой, соответствующей квантовому состоянию, соответственно, 1, 2 и 3. Радиус винтовой траектории этих тел пропорционален квадрату квантового числа. Пунктирной линией показана траектория тела, которое за то же самое время успевает совершить более одного оборота вокруг оси O-O, т.е. обладающего меньшей длиной волны. Точечной линией показана траектория тела, которое за то же самое время не успевает совершить оборот вокруг оси O-O, т.е. обладающего большей длиной волны.
В главе «Теория гравидинамического взаимодействия» мы нашли формулу длины волны для макротел по форме совпадающей с формулой де Бройля:
R=S/mV (22.2).
Эта формула верна при равной поступательной и тангенциальной скорости. В макромире, в отличие от микромира, при интерференции волн одинаковой длины, но разной амплитуды возможно слипание частиц в единый агломерат из-за действия закона всемирного тяготения. Поэтому макротела с одной и той же длиной волны могут иметь в космическом пространстве (на единицу массы) кратное значение момента импульса S на винтовой траектории
S=S0∙n (22.3)
за счет кратного значения VtR. В (22.3) n имеет тот же смысл, что и в формуле (22.1). В микромире слипание свободных частиц невозможно из-за электростатического отталкивания одноименно заряженных частиц и отсутствия притяжения между «нейтральными» частицами. Таким образом, в формуле (22.2):
S=VtmR∙n (22.4),
а V в знаменателе имеет смысл поступательной скорости:
V=Vf (22.5).
Подставив (22.4) и (22.5) в (22.2), найдем (22.1). Отсюда следует вывод, что центральное тело образует спутниковую систему путем захвата космических тел с одинаковой длиной волны, но кратным значением VtR относительно минимального значения при n=1. При этом строение образующейся системы следует теории Бора для атома водорода с тем отличием, что «возбужденные» орбиты устойчивы, т.к. спутники не имеют возможности что-либо излучать для перехода на более низкую орбиту, чтобы система в целом перешла в состояние с минимумом потенциальной энергии. Из строения Солнечной системы и спутниковых систем видно, что «длина волны» захватываемых тел земной группы отличается от «длины волны» тел юпитерной группы, т.е. Солнечная система напоминает двухэлектронный атом с двумя независимыми системами энергетических уровней макротел.
Подставив (22.3) в (22.2) и учитывая, что
S0=mV0tR0 (22.6),
а V0t =Vf∙n, получим:
R=R0n2 (22.7),
что соответствует реальному распределению планет или спутников при данной «длине волны». Ранее мы формулой (22.7) пользовались исходя из наблюдательных фактов, а не теоретических расчетов.
Из условия равновесия космического тела на устойчивой орбите легко найти критерий устойчивости орбитального движения, который зависит только от массы центрального тела и не зависит от квантового числа космического тела:
RV2=GM (22.8),
где R – радиус орбиты, V –
орбитальная скорость, G – гравитационная постоянная, M – масса
центрального тела. Из (22.8) можно получить длину волны, которая поглощается
данным центральным телом, учитывая, что ![]() =2
=2![]() ∙R0:
∙R0:
![]() (22.9).
(22.9).
Поскольку V0 не зависит от массы центрального тела, что было показано ранее, то спутниковую систему образуют космические тела, у которых длина волны пропорциональна массе центрального тела, что и наблюдается в действительности – чем больше масса центрального тела, тем дальше расположены спутники.
Учитывая вышеизложенное, необходимо дать более общую формулировку движения макротел: все свободные тела двигаются по винтовой линии. При этом мы будем иметь в виду, что в микромире тангенциальная скорость движения равна поступательной, а в макромире тангенциальная скорость равна поступательной только в первом квантовом состоянии тела.
22.1. Гравидинамическое взаимодействие и эволюция орбит
 |
Как известно, в настоящее время отсутствует объяснение, почему все планеты двигаются по орбитам в сторону вращения Солнца в одной плоскости, почему то же самое делают члены спиральных галактик. Гравидинамическое взаимодействие позволяет легко объяснить как этот факт, так и многие другие особенности строения Солнечной системы и разного вида галактик. Мы знаем, что одноименные магнитные полюса отталкиваются, а разноименные притягиваются. Из главы 11.2.2 можно догадаться, что гравидинамические полюса действуют противоположным образом. Сначала определимся в понятии «полюс». Если электрический или гравитационный заряд движется так, что при этом ометает некоторую площадь, то мы говорим, что возникает магнитный (гравидинамический момент) имеющий два полюса, как показано на фигуре 22.1.1.
На фигуре изображено движение положительного электрического заряда по круговой орбите при котором возникает магнитный момент и два магнитных полюса – северный N и южный S. При таком же движении гравитационного заряда из антиматерии картина возникновения двух гравидинамических полюсов аналогична. Очевидно, что орбитальный гравидинамический момент 1 много больше собственного гравидинамического момента 2, т.к. величина этих моментов определяется произведением гравитационного «тока» на ометаемую им площадь по формуле:
![]() (22.1.1),
(22.1.1),
где: K – коэффициент, величина которого значительно возрастает
при приближении скорости движения к световой скорости из-за такого же
увеличения гравидинамического поля (см. главу 11.1), ![]() - гравитационный «ток», где V – скорость движения гравитационного заряда
- гравитационный «ток», где V – скорость движения гравитационного заряда ![]() , r – радиус орбиты или эффективный радиус собственного вращения
космического тела.
, r – радиус орбиты или эффективный радиус собственного вращения
космического тела.
Из-за взаимного притяжения гравидинамических моментов 1 и 2 собственное вращение планет происходит в направлении их орбитального движения и в направлении вращения Солнца. Исключения из этого вывода скоро станут ясны.
Как будут взаимодействовать гравидинамические полюса между собой видно из фигуры 22.1.2.
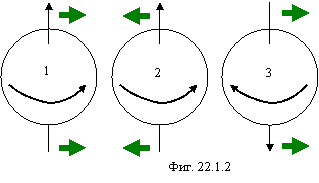 |
Ближе расположенные друг к другу части зарядов № 1 и №2 двигаются встречно и притягиваются, а ближе расположенные друг к другу части зарядов №2 и №3 двигаются в одном направлении и отталкиваются в соответствии с концепциями действия гравидинамического поля изложенными в главе 11.2.2. Поэтому одноименные гравидинамические полюса притягиваются, а разноименные отталкиваются друг от друга.
 |
На фигуре 22.1.3. показано движение некоторого космического тела до захвата его Солнечной системой. Очевидно, что захват может произойти в любой фазе этого движения. При этом важно отметить, что возникшая эллиптическая орбита в любом случае будет расположена под углом, примерно, 450 к винтовой траектории, а направление собственного вращения тела сохранится неизменным из-за гироскопического эффекта. Таким образом, захваченное тело движется в Солнечной системе под любым произвольным углом к экваториальной плоскости Солнца, который определяется не только фазой движения в момент захвата, но и первоначальным направлением оси винтовой траектории «свободного» космического тела. Поэтому и направление собственного вращения может быть произвольным. Однако, все это справедливо в начальный момент после захвата. В дальнейшем плоскость орбиты поворачивается таким образом, чтобы орбитальное движение было прямым из-за притяжения одноименных гравидинамических полюсов Солнца и орбитального гравидинамического момента. Направление вращения тоже стремится стать прямым (в сторону орбитального движения), но гироскопический эффект этому сильно препятствует, поэтому поворот оси вращения происходит значительно медленнее и сопровождается прецессией этой оси. Значительная временная разница в эволюции орбиты и оси вращения позволяет судить о возможном направлении прихода тела в Солнечную систему и о времени этого прихода.
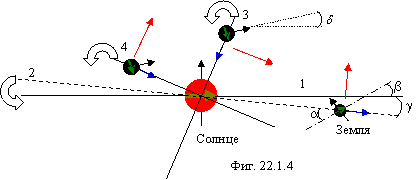 |
На фигуре 22.1.4 показана часть Солнечной системы в экваториальной
плоскости Солнца 1. Для ориентировки пунктирной линией показана плоскость
эклиптики 2 (орбиты Земли), а штрих-пунктирной линией показана экваториальная
плоскость Земли. Угол ![]() равен
23,450, угол
равен
23,450, угол ![]() равен
7,20, тогда угол
равен
7,20, тогда угол ![]() равен 16,250. Синими стрелками
показано направление орбитального движения, а красные стрелки показывают
направление орбитального гравидинамического момента для данной орбиты. Очевидно,
что в данном случае, наклоны плоскостей орбит планет и прочих членов Солнечной
системы по отношению к плоскости эклиптики необходимо пересчитать по отношению
к экваториальной плоскости Солнца, т.к. именно оно заставляет все
гравидинамические моменты орбитальные и собственные выстроить в направлении
своего собственного гравидинамического момента. Положение тела после захвата
зависит от его положения на винтовой траектории в момент захвата и угла
равен 16,250. Синими стрелками
показано направление орбитального движения, а красные стрелки показывают
направление орбитального гравидинамического момента для данной орбиты. Очевидно,
что в данном случае, наклоны плоскостей орбит планет и прочих членов Солнечной
системы по отношению к плоскости эклиптики необходимо пересчитать по отношению
к экваториальной плоскости Солнца, т.к. именно оно заставляет все
гравидинамические моменты орбитальные и собственные выстроить в направлении
своего собственного гравидинамического момента. Положение тела после захвата
зависит от его положения на винтовой траектории в момент захвата и угла ![]() между осью вращения тела
и экваториальной плоскостью Солнца. Если, например, тело было захвачено в
дальней точке, где оно изображено на фигуре 22.2.3, то после захвата орбита
тела займет положение 3, а если захвачено в ближней точке, то после захвата
орбита тела займет положение 4. В первое время после захвата орбита тела часто
будет иметь кроме большого эксцентриситета еще и большие углы наклона к
экваториальной плоскости Солнца. В положении 3 тело обладает обратным
орбитальным движением и обратным вращением, но в результате гравидинамического
взаимодействия с Солнцем орбита будет поворачиваться против часовой стрелки
(показано белыми стрелками) и в конце концов движение захваченного тела станет
«нормальным» - прямое обращение и прямое вращение вблизи плоскости солнечного
экватора. В положении 4 тело сразу обладает прямым движением и вращением,
поэтому большого поворота орбиты не требуется. При повороте орбиты собственная
ось вращения остается в пространстве неизменной как у гироскопа, поэтому
поворот этой оси значительно отстает по времени от орбитального поворота. При
желании, читатель может подробно рассмотреть результаты захвата
правовращающихся и левовращающихся космических тел, приближающихся под
различными углами к экваториальной плоскости Солнца и получить характеристики
любого члена Солнечной системы. Особенно интересен случай, когда после захвата
движение тела становится прямым, а собственное вращение обратным. В этом случае
гравидинамическое взаимодействие вынуждено тормозить вращение тел, а затем
заставить вращаться в прямом направлении. По результатам такого качественного
анализа можно судить не только о приблизительном времени захвата, но и о
направлении, откуда космическое тело к нам пришло.
между осью вращения тела
и экваториальной плоскостью Солнца. Если, например, тело было захвачено в
дальней точке, где оно изображено на фигуре 22.2.3, то после захвата орбита
тела займет положение 3, а если захвачено в ближней точке, то после захвата
орбита тела займет положение 4. В первое время после захвата орбита тела часто
будет иметь кроме большого эксцентриситета еще и большие углы наклона к
экваториальной плоскости Солнца. В положении 3 тело обладает обратным
орбитальным движением и обратным вращением, но в результате гравидинамического
взаимодействия с Солнцем орбита будет поворачиваться против часовой стрелки
(показано белыми стрелками) и в конце концов движение захваченного тела станет
«нормальным» - прямое обращение и прямое вращение вблизи плоскости солнечного
экватора. В положении 4 тело сразу обладает прямым движением и вращением,
поэтому большого поворота орбиты не требуется. При повороте орбиты собственная
ось вращения остается в пространстве неизменной как у гироскопа, поэтому
поворот этой оси значительно отстает по времени от орбитального поворота. При
желании, читатель может подробно рассмотреть результаты захвата
правовращающихся и левовращающихся космических тел, приближающихся под
различными углами к экваториальной плоскости Солнца и получить характеристики
любого члена Солнечной системы. Особенно интересен случай, когда после захвата
движение тела становится прямым, а собственное вращение обратным. В этом случае
гравидинамическое взаимодействие вынуждено тормозить вращение тел, а затем
заставить вращаться в прямом направлении. По результатам такого качественного
анализа можно судить не только о приблизительном времени захвата, но и о
направлении, откуда космическое тело к нам пришло.
22.2. Две большие ошибки: первый закон Ньютона и инерциальные системы отсчета
Рассмотрим движение свободного тела. Официальная физика считает, что это движение подчиняется первому закону Ньютона и, пока, в этом никто не сомневается, кроме меня. В главе 2 приведена верная мысль доктора М.Л. Клебанова, которую можно сформулировать так: «любое свободное тело не свободно от собственной массы». Предположим, что некоторому телу (микрочастице или макротелу) сообщили некоторую скорость V. В общем случае направление вектора скорости тела и направление оси его вращения произвольны, что показано на фигуре 22.2.1.
Разложим вектор скорости на две взаимно перпендикулярные составляющие: V1 на направление оси вращения тела и V2 перпендикулярную этой оси.
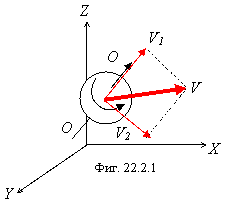 |
По теории новой физики гравидинамическое поле возникает при любом движении гравитационных зарядов. Вращающаяся масса подобна контуру с гравитационным «током», создающим индукцию гравидинамического поля B, направленную вдоль оси вращения. Таким образом, ситуация становится аналогичной движению электрического заряда перпендикулярно магнитному полю. На тело действует гравидинамический аналог силы Лоренца, заставляющий его двигаться по окружности (по часовой стрелке, если смотреть вдоль оси вращения). Второе независимое движение происходит равномерно вдоль оси вращения тела, т.к. при этом гравидинамическое воздействие равно нулю. Таким образом, любое свободное тело движется по правовинтовой или левовинтовой траектории в зависимости от взаимного направления вектора собственного вращения и вектора V1. Тело, изображенное на фигуре 22.2.1 будет двигаться по правовинтовой траектории. Как следствие винтового движения свободных тел, выражающееся в их «корпускулярно-волновом дуализме», можно утверждать об ошибочности первого закона Ньютона и принципиальном отсутствии «инерциальных систем отсчета», т.к. винтовое движение абсолютно. У не свободных тел круговое движение сохраняется, а поступательное, естественно, исчезает, превращаясь в потенциальную энергию универсального отталкивания (глава 1).
За одно и то же время тело проходит путь, равный «длине волны де Бройля» в поступательном перемещении и некоторую длину окружности в тангенциальном вращении вокруг оси винтовой траектории. Эта длина составляет целое число длин волн в поступательном направлении (на орбите укладывается целое число «длин волн де Бройля»), поэтому можем записать:
![]() (22.2.1),
(22.2.1),
откуда:
![]() (22.2.2).
(22.2.2).
В главе 20 показано, что орбитальный радиус космических тел пропорционален квадрату целых чисел, начиная от основного состояния с минимальным радиусом орбиты, поэтому из (22.2.2):
![]() (22.2.3).
(22.2.3).
Очевидно, что общая энергия при винтовом движении равна сумме кинетической энергии поступательного движения и потенциальной энергии универсального отталкивания (глава 1) на окружности поперечного сечения винтовой траектории:
![]() (22.2.4).
(22.2.4).
С учетом последнего выражения, формула (22.2.3) запишется так:
![]() (22.2.5).
(22.2.5).
Возникает вопрос: почему отношение потенциальной энергии к кинетической перед захватом космических тел с винтовой траектории на круговую орбиту имеет только целочисленные значения от единицы и выше? Единственное объяснение я вижу в том, что космические тела имеющие одинаковое значение произведения Vr имеют и одинаковую «длину волны де Бройля» поэтому способны объединяться между собой («интерферировать») при длительном путешествии в космических просторах. Закон равного распределения энергии по степеням свободы требует равенства V1 и V2 , т.е. n=1, но в зависимости от индукции гравидинамического поля данного тела дополнительный гравидинамический аналог силы Лоренца уменьшает радиус винтовой траектории одновременно увеличивая потенциальную энергию не влияя на кинетическую энергию тела. Можно было бы сочинить высосанную из пальца формулу, описывающую целочисленные значения n для метеоритного и кометного материала, но я этого делать не буду, оставляя решение этой задачи для последователей новой физики, которые сначала поймут физические причины целочисленности n, а затем нетрудно написать и соответствующую формулу.
Теперь рассмотрим движение не свободного тела. Скептик, прочитав начало главы, посчитает ее за бред сумасшедшего. Бросим камень вдоль поверхности земли и никакого винтового движения мы не увидим. Чтобы он понял суть проблемы, напомню, что при обычных скоростях движения гравидинамическое поле очень слабое, поэтому размеры винтовой траектории имеют космические масштабы. Кроме того, если в микромире гравитационное взаимодействие нисколько не влияет на гравидинамическое, то в макромире исход конкуренции между гравитационным и гравидинамическим взаимодействием зависит от конкретных параметров тел. Брошенный вдоль поверхности земли камень уже не свободен, поэтому может двигаться в конечном итоге только по круговой орбите. Чтобы Земля не препятствовала его движению, предположим, что в момент броска она сжалась в точку в бывшем центре Земли и не изменила массу. Момент импульса камня относительно центра Земли:
![]() (22.2.6),
(22.2.6),
где: m – масса камня, v0 – его начальная скорость движения, R – радиус Земли.
Энергия связи камня с Землей:
![]() (22.2.7)
(22.2.7)
является алгебраической суммой потенциальной энергии притяжения и потенциальной энергией универсального отталкивания. G – гравитационная постоянная, M – масса Земли, v и r текущие значения скорости и радиуса орбиты. Мы полагаем, что камень в конце-концов окажется в потенциальной яме, т.е. займет стационарную круговую орбиту, поэтому надо найти минимум (22.2.7). Но прежде нужно выразить скорость движения через радиус орбиты. Пользуясь законом сохранения момента импульса тела, аналогично (22.2.6) можем записать:
![]() (22.2.8).
(22.2.8).
Подставив (22.2.8) в (22.2.7), найдем:
![]() (22.2.9).
(22.2.9).
Найдем минимум (22.2.9):
![]() (22.2.10),
(22.2.10),
где: r0 – радиус стационарной
круговой орбиты, ![]() -
постоянная,
-
постоянная, ![]() =vr, т.к. m остается
постоянной.
=vr, т.к. m остается
постоянной.
Подставляя в (22.2.10) численные значения при v0 = 10 м/сек, найдем, что если бы Земля не мешала движению камня, он занял бы круговую орбиту вокруг ее центра радиусом 10,2 метра. Скорость его движения на этой орбите будет 6250 км/сек.
Теперь нужно ответить на вопрос: почему почти все микрочастицы обладают
одним и тем же моментом импульса на винтовой траектории равным ![]() ? Хотя официальная физика
отделяет бозоны от фермионов, тем не менее, при определении «длины волны» тех и
других пользуется формулой де Бройля, которая предусматривает момент импульса
их одинаковым, иначе получатся расхождения с экспериментом в определении «длины
волны» этих частиц. Поэтому постоянная Планка h
является не «квантом действия», как считает официальная физика, а обыкновенным
моментом импульса частицы:
? Хотя официальная физика
отделяет бозоны от фермионов, тем не менее, при определении «длины волны» тех и
других пользуется формулой де Бройля, которая предусматривает момент импульса
их одинаковым, иначе получатся расхождения с экспериментом в определении «длины
волны» этих частиц. Поэтому постоянная Планка h
является не «квантом действия», как считает официальная физика, а обыкновенным
моментом импульса частицы:
![]() (22.2.11),
(22.2.11),
причем этот момент импульса относится не к собственному моменту импульса, а к моменту импульса на витках винтовой траектории, который значительно больше собственного момента. Из (22.2.10) выразим радиус винтовой траектории частицы через ее скорость:
![]() (22.2.12),
(22.2.12),
где ![]() не
постоянная тонкой структуры, а постоянная величина произведения vr при изменении этих сомножителей,
когда масса тела при этом изменении остается постоянной, поэтому (22.2.12) –
прямое следствие закона сохранения момента количества движения тела.
не
постоянная тонкой структуры, а постоянная величина произведения vr при изменении этих сомножителей,
когда масса тела при этом изменении остается постоянной, поэтому (22.2.12) –
прямое следствие закона сохранения момента количества движения тела.
Из того факта, что величина ![]() планет Солнечной системы увеличивается с
увеличением расстояния от Солнца (глава 21, фигура 21.3) можно сделать вывод,
что
планет Солнечной системы увеличивается с
увеличением расстояния от Солнца (глава 21, фигура 21.3) можно сделать вывод,
что ![]() обратно
пропорциональна индукции B гравидинамического
поля:
обратно
пропорциональна индукции B гравидинамического
поля:
![]() (22.2.13).
(22.2.13).
Если для космических тел подсчет индукции гравидинамического поля вдоль оси их собственного вращения сложен из-за разной скорости вращения, разной плотности материала космических тел и их разной величины, то для микрочастиц этот расчет значительно упрощается. Компоненты микрочастиц двигаются со скоростью света, поэтому создают максимально возможную индукцию гравидинамического поля вдоль оси их орбиты. Поэтому можно записать:
![]() (22.2.14),
(22.2.14),
где ![]() -
удельная индукция гравидинамического поля единичной массы, а m – масса частицы. Подставив
(22.2.14) и (22.2.13) в (22.2.12), найдем:
-
удельная индукция гравидинамического поля единичной массы, а m – масса частицы. Подставив
(22.2.14) и (22.2.13) в (22.2.12), найдем:
![]() (22.2.15).
(22.2.15).
Размерность гравидинамической индукции в системе СГС: [B]=сек×см-2,
а размерность удельной индукции [![]() ]=эрг-1×сек-1.
]=эрг-1×сек-1.
Чтобы получить момент импульса частицы на витках винтовой траектории, умножим (22.2.15) на mv:
![]() (22.2.16).
(22.2.16).
Таким образом, мы выяснили еще один физический смысл постоянной Планка (момента импульса частицы). Оказывается, он равен обратной величине удельной индукции гравидинамического поля и для всех частиц имеет одно и то же значение, т.к. их компоненты двигаются с одинаковой скоростью равной скорости света.
Комментарии автора к главе 22.2:
1. Критический взгляд на законы Ньютона.
Первый закон Ньютона. «Свободные тела двигаются равномерно и прямолинейно». В главе 2 показано, что любые свободные тела двигаются по винтовой траектории, поэтому первый закон Ньютона не применим к самому телу, но к математической абстракции – оси винтовой траектории тела.
Второй закон Ньютона. «F=ma – ускорение приобретаемое телом пропорционально
действующей на тело силе и обратно пропорционально массе тела». Легко показать,
что в некоторых случаях второй закон Ньютона приводит к абсурдным результатам.
Будем действовать с силой 1 дина на электрон массой 9,1×10-28 г. В конце первой
секунды по второму закону Ньютона электрон должен достичь скорости больше
скорости света в 3×1016
раз. Очевидно, что второй закон Ньютона надо согласовать с релятивистским
увеличением массы тела, например, так: 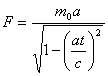 , где t –
время действия силы F на ускоряемую массу,
которая покоилась.
, где t –
время действия силы F на ускоряемую массу,
которая покоилась.
Третий закон Ньютона. «Действие равно противодействию». В главе 1.2 дан анализ эксперимента, когда гирю бросают на подушку. В ней показано, что третий закон Ньютона верен только в условиях отсутствия сил инерции в состоянии статического или динамического равновесия.