21. ТЕОРИЯ ЗАХВАТА КОСМИЧЕСКИХ ТЕЛ

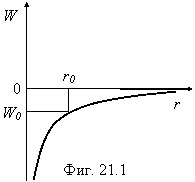
Относительно захвата одного космического тела другим, современная космология дает однозначный ответ - он невозможен без присутствия третьего тела. Объяснение очень просто. Гравитационная энергия взаимодействия тел превращается в кинетическую энергию “падения” их друг на друга. Если захватываемое тело мало по сравнению с захватывающим (центральным), то захватываемое тело опишет вокруг центрального тела параболическую траекторию и вновь уйдет в бесконечность. Основная причина невозможности захвата состоит в том, что захватываемое тело неспособно каким-либо способом достаточно быстро растерять избыточную энергию. Потеря энергии возможна только при длительном обращении вокруг центрального тела под действием приливных и других сил, которые все вместе слишком малы для реализации захвата сразу. Изменение потенциальной энергии двух взаимодействующих за счет гравитации тел так, как это себе представляет современная космология представлено на фигуре 21.1.

В любой точке r₀ потенциальная энергия тела m (центральное тело М находится в начале координат), равная W₀ одновременно равна кинетической энергии тела m, что требует закон сохранения энергии (общая энергия равна нулю). Поэтому в любой точке тело m способно “отскочить” на бесконечно большое расстояние от М и его захват невозможен. “В рамках гравитационной задачи двух тел захват или выброс невозможны, поскольку отсутствуют факторы, способные изменить полную механическую энергию тел”. Физика космоса, “Советская энциклопедия”, М., 1976, стр. 74. Для того чтобы захват произошел, тело m на бесконечно большом расстоянии от М должно обладать отрицательной энергией, что физически невозможно, т.к. в этом состоянии потенциальная энергия m равна нулю, а кинетическая энергия всегда положительна. Получается что тело, принадлежащее Солнечной системе, обладает некоторой полной энергией, имеющей отрицательное значение, поэтому оно не может покинуть систему (выброс невозможен). Тело не принадлежащее Солнечной системе обладает некоторой полной энергией (кинетической) всегда имеющей положительное значение, поэтому оно не может быть захвачено. Таким образом, с точки зрения современной науки, любая космическая система является изолированной по отношению к массообмену. Прямым следствием этого является вывод о том, что все тела, принадлежащие Солнечной системе, принадлежали ей всегда, следовательно, Солнечная система могла образоваться только одновременно и из одного протопланетного облака.

Рассуждения ортодоксов в обсуждаемом вопросе настолько убедительны, что, казалось бы, альтернативы им не существует. Однако наблюдательные данные, например, обратное движение некоторых спутников, обратное вращение некоторых планет, постоянная очистка от межпланетной пыли, метеоритов и комет и множество других со всей очевидностью показывают ошибочность представлений официальной космологии, как в отношении образования Солнечной системы, так и в отношении теории гравитационного взаимодействия в целом.

Новая физика совсем по иному представляет себе гравитационное взаимодействие двух тел. Потенциальная энергия связи этих тел складывается из потенциальной энергии притяжения и потенциальной энергии отталкивания:

                                      (21.1).

Учитывая закон сохранения момента импульса, который для неизменной массы будет:

 Vr=                                                 (21.2)

и подставляя (21.2) в (21.1), получим:

                                    (21.3).

 Дифференцируя (21.3) по радиусу и приравнивая производную нулю, найдем радиус орбиты, при котором энергия связи имеет минимум:

                                               (21.4).

Подставив (21.4) в (21.3), найдем энергию связи двух тел:

                                           (21.5).

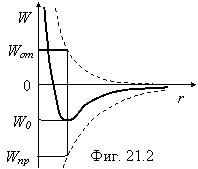
Изменение потенциальной энергии представлено на фигуре 21.2.

Как видно из рисунка, тело m будет двигаться вокруг центрального тела по устойчивой круговой орбите радиуса r₀, т.к. система при этом имеет минимум потенциальной энергии. Если m сообщить некоторую дополнительную энергию, не превышающую ту, что определяется формулой (21.5), то орбита станет эллиптической. Если избыточная энергия будет равна энергии связи, то орбита станет параболической и система разрушится из-за удаления m в бесконечность. Закон сохранения энергии в случае захвата выполняется по той причине, что половина энергии притяжения переходит в энергию отталкивания и, чтобы удалить m в бесконечность, необходимо сообщить этому телу энергию, определяемую выражением (21.5), т.е. вторую половину, поэтому общая энергия на бесконечном удалении тел друг от друга снова станет нулевой. Таким образом, захват неизбежен для любого тела, если его кинетическая энергия на бесконечно большом расстоянии от М не превышает энергию связи (21.5) на устойчивой орбите.

Предположим, что на бесконечно большом расстоянии от M тело m обладает кинетической энергией E_k составляющей некоторую долю K от энергии связи W₀ на будущей круговой орбите:

                                            (21.6).

 Тогда уравнение (21.3) можно записать так:

                               (21.7).

Подставляя (21.6) в (21.7) и учитывая соотношения (21.4) и (21.5), найдем формулы для перигелия и афелия орбиты:

(21.8),                                     (21.9).

Приравнивая (21.8) выражению (13.19), найдем эксцентриситет орбиты:

                                             (21.10).

Формула (21.10) показывает, что вновь захваченные тела имеют орбиты с большими эксцентриситетами. Например, тело, имеющее кинетическую энергию в бесконечности составляющую всего 1% от энергии связи на круговой орбите (К=0,01W₀) будет иметь эксцентриситет равный 0,1.

Если в формулу (21.10) подставить (21.6), где , а также (21.4) и (21.5) и учесть, что =r₀V₀, где V₀ - орбитальная скорость на круговой орбите, то мы получим еще одну формулу для эксцентриситета орбиты захваченного тела:

                                              (21.11),

где:  - скорость тела m в бесконечности,

V₀ - скорость тела m на круговой орбите, которую оно займет после полного расходования избыточной энергии E_k.

Рассмотрим механизм захвата и эволюции орбиты захваченного тела более подробно.

Предположим, что тело движется в Солнечной системе с эксцентриситетом равным 1. По современным представлениям это тело, пройдя перигелий своей орбиты, удалится снова в бесконечность и не может быть захвачено. По представлениям новой физики такое движение тела эквивалентно «соударению» с Солнечной системой и отскоком тела назад. При этом по закону сохранения импульса тело передаст часть своего импульса Солнечной системе в целом и обратная ветвь траектории будет представлять собой уже не параболу, а эллипс, т.е. эксцентриситет орбиты окажется меньше 1. Таким образом, тело окажется захваченным и, при каждом прохождении перигелия, оно будет передавать Солнечной системе порции своей избыточной энергии до тех пор, пока орбита тела не станет круговой. Очевидно, что для этого число оборотов n вокруг Солнца должно быть бесконечным, т.к. передаваемые порции все время уменьшаются. Поэтому система энергетических уровней захваченного тела очень похожа на систему энергетических уровней атома (см. главу «Теория водородоподобного атома»). Круговая орбита в этих случаях достигается при n . Здесь следует уточнить, что круговая орбита не может быть достигнута ни в водородоподобном атоме, ни в космической системе. Поэтому говорить можно лишь о некоторой равновесной орбите, близкой к круговой, т.к. в обоих случаях возбужденное состояние возникает при малейшем воздействии на систему, поскольку уровни энергии вблизи круговой орбиты наиболее тесно расположены. В первом случае атом находится в возбужденном состоянии даже при температуре абсолютного нуля, а во втором случае возбужденное состояние космических тел поддерживается постоянным выпадением на них метеоритов, комет и космической пыли.

По закону сохранения импульса:

                                     (21.12),

где: m – масса захватываемого тела,

V_f - «избыточная» скорость m «вперед»,

V_b  - «избыточная» скорость m «назад»,

M – масса захватывающего тела,

V_M - скорость приобретаемая M.

В (21.12) массу остальных членов системы не учитываем, в противном случае под M нужно понимать общую массу системы.

Энергетический баланс:

                                    (21.13).

Решая совместно (21.12) и (21.13), найдем:

                                     (21.14).

 Из (21.14): ,  и т.д., следовательно, для числа оборотов n формула (21.14) примет вид:

                                    (21.15).

 Подставив (21.15) в (21.11), найдем изменение эксцентриситета:

                                       (21.16).

 Обратившись к формуле (20.1.6), ее можно объяснить также и тем, что малые массы теряют меньше энергии на каждом обороте и дольше сохраняют большой эксцентриситет орбиты. Эволюция орбит больших масс происходит значительно быстрее.

В (21.16) при n=0 (захвата еще нет) e=1, а при n, e0, т.к. дробь в (21.16) всегда меньше 1.

Третий закон Кеплера можно преобразовать к виду:

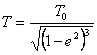                                       (21.17),

 где: T – период вращения на эллиптической орбите,

T₀ – период вращения на круговой орбите,

e – эксцентриситет.

Потеря энергии тела m на каждом обороте вокруг центрального тела M составит:

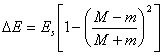                                  (21.18),

 где: E_s – «избыточная» энергия тела m.

Пользуясь формулами (21.16) и (21.17) легко посчитать эволюцию орбиты захваченного тела. Для простоты, массы тел будем считать неизменными за период эволюции.

Луна. Перед захватом Землей, Луна должна была иметь значение a почти такое же, как у Земли, чтобы равновесный радиус ее орбиты вокруг Солнца был близок земному радиусу. Луна перед захватом Солнечной системой не могла иметь скорость 30 км/сек и e=1, т.к. после прохождения перигелия, ее эксцентриситет останется слишком большим (e=0,99999992614) и первый оборот вокруг Солнца она совершала бы 17,6 млрд. лет. В этом случае захват Луны Землей невозможен, кроме случайного прямого попадания. Более вероятна скорость Луны в бесконечности меньше 30 км/сек, например 20 км/сек. В этом случае орбита Луны в Солнечной системе будет иметь начальный эксцентриситет 0,667 с периодом обращения 2,4 года. В двух противоположных точках на линии, перпендикулярной главной оси орбиты и проходящей через центр Солнца, орбиты Земли и Луны будут пересекаться (как в атомных орбитах). Вблизи этих точек возможен захват Луны Землей. Сейчас равновесный эксцентриситет орбиты Луны составляет 0,0549 и средняя скорость орбитального движения, около 1 км/сек. Предположим, что в начале захвата Луна имела такую же скорость относительно Земли, т.е. двигаясь к Земле по параболической траектории, Луна после прохождения перицентра приобретет эллиптическую траекторию вокруг Земли с эксцентриситетом 0,9757. Период первого оборота вокруг Земли составит 7 лет, на втором обороте эксцентриситет орбиты уменьшится до 0,952, а период до 2,6 года и т.д. Равновесная орбита близкая к современной будет достигнута за 120 оборотов и на это потребуется всего около 25 лет. Такая быстрая эволюция орбиты Луны связана с ее большой массой относительно Земли.

Земля. Если считать, что Земля перед захватом имела скорость 30 км/сек (e=1), то после первого прохождения перигелия эксцентриситет ее орбиты станет равным 0,99999399, а время первого оборота после захвата будет 24 миллиона лет. На втором обороте e=0,99998798 и T=8,5 миллионов лет и т.д. Равновесный эксцентриситет орбиты будет достигнут за 800000 оборотов, примерно, за 102 миллиона лет.

Для проверки излагаемых взглядов на эволюцию орбит нужна значительная масса спутника по отношению к центральному телу и значительный эксцентриситет его орбиты. В Солнечной системе имеется два кандидата для проверки: Меркурий и Нереида (спутник Нептуна). Эксцентриситет Меркурия 0,2056, а отношение к массе Солнца 1,66×10^-7, эксцентриситет Нереиды 0,75, а отношение к массе Нептуна 3×10^-7. Если учесть, что на Меркурий должно выпадать ощутимое количество космического материала, который увеличивает равновесный эксцентриситет его орбиты, то наблюдение за орбитой Нереиды более предпочтительно.

Нереида. По литературным данным (Е.Н. Слюта и др. Сравнительная планетология. Москва, «Наука», 1995, стр.88) радиус Нереиды 170 км. Масса ее неизвестна, но, приняв плотность 1,5 г/см3, найдем m=3,087×10²⁰ г. Масса Нептуна 102×10²⁷ г. Если Нереида имела параболическую траекторию перед захватом Нептуном, то для достижения эксцентриситета 0,75 она должна была совершить 47550755 оборотов вокруг Нептуна. Сейчас период обращения Нереиды вокруг Нептуна составляет 8643,1 часа. Расчет показывает, что с каждым оборотом этот период должен уменьшаться на 0,73 секунды.

Достаточно быстрая эволюция орбиты возможна только для захваченных тел, масса которых не менее 10^-7 массы центрального тела. Менее массивные тела «отскакивают» от центрального тела практически без потери энергии и эволюция их орбиты обусловлена другими причинами:

1. Все тела Солнечной системы подвержены действию «солнечного ветра». При движении по эллиптической орбите навстречу «солнечному ветру» потеря избыточной энергии превышает ее поступление при удалении тела от Солнца.

2. Точно такой же механизм действует при облучении тела фотонами, излучаемыми Солнцем. При движении навстречу Солнцу тело поглощает более коротковолновые фотоны, чем при движении от Солнца.

3. Кометы представляют собой ледяные глыбы из воды, аммиака и метана с «начинкой» из метеорных тел. Поэтому кометы достаточно быстро разрушаются под действием радиации и приливного действия Солнца и их орбиты достаточно быстро эволюционируют. В итоге от комет остается метеорный рой, в котором эволюция орбит отдельных тел зависит от их массы.

Во всех этих случаях при каждом обороте вокруг Солнца тело теряет порцию избыточной энергии, и его орбита приближается к круговой.

1. Поток протонов «солнечного ветра» вблизи Земли составляет ~2,5 протонов/см²×сек, а скорость его 400 км/сек (Физика космоса. М., 1976, стр. 555-556). Астероид радиусом r, движущийся в окрестностях Земли по эллиптической орбите к Солнцу встретит «солнечный ветер» со скоростью 430 км/сек, а при движении от Солнца – 370 км/сек. Потеря избыточной кинетической энергии астероида за одну секунду составит:

                           (21.19),

где: S – площадь сечения астероида (м²),

m_p – масса протонов попадающих в секунду на 1м² поперечного сечения астероида (кг).

Полная избыточная энергия астероида, движущегося с эксцентриситетом равным 1, в окрестностях Земли составит:

                                         (21.20),

где: m – масса астероида (кг),

V – скорость астероида (30000 м/сек).

Плотность материала астероида примем равной 3000 кг/м³. Разделив (21.20) на (21.19), найдем время полной потери избыточной энергии астероида. При этом он будет двигаться по круговой орбите. Здесь мы делаем грубую ошибку в расчетах, т.к. (21.19) зависит от положения астероида на орбите. Точный расчет невозможен, поэтому полученную ниже формулу нужно считать лишь первым приближением:

T=1,794×10¹⁶r  (сек)                                  (21.21).

Астероид радиусом 1 м по формуле (21.21) займет круговую орбиту за 568 миллионов лет, а пылинка радиусом 1 мкм за 568 лет. За время существования Солнечной системы (5 млрд. лет) потерять всю избыточную энергию за счет этого эффекта могли только астероиды с радиусом меньше 10 м. Поэтому тела большего размера имеющие небольшой эксцентриситет орбиты могли быть захвачены с относительно небольшой начальной скоростью.

2. В главе «Движущийся в пустоте наблюдатель, источник неподвижен» получены формулы для частоты света, воспринимаемого наблюдателем, двигающимся к источнику:  и от источника: . Разница энергий фотонов, воспринимаемых космическим телом, которая будет израсходована на уменьшение избыточной энергии этого тела, составит:

                                        (21.22).

Солнечная постоянная равна 1400 вт/м² (Физика космоса. М., 1976, стр. 551). Если космическое тело движется вблизи Земли с параболической скоростью 30 км/сек, то с учетом (21.22) на каждом обороте вокруг Солнца мощность потери энергии:

(вт)                                      (21.23),

где r – радиус тела.

Разделив (21.20) на (21.23) получим:

T=2,04×10⁵r  (лет)                                      (21.24).

Формула (21.24) показывает, что под действием фотонного излучения Солнца эволюция орбиты космического тела протекает значительно быстрее, чем под действием «солнечного ветра». Тот же астероид радиусом 1 м займет круговую орбиту не через 568 миллионов лет, а через 204000 лет.

Спутники планет при движении по круговой орбите не обладают избыточной энергией, но все равно постоянно теряют энергию по изложенному механизму, т.к. двигаются то к Солнцу, то от Солнца, поэтому вышеприведенный расчет для спутников планет оказывается более точным. Например, Луна потеряет полностью всю энергию орбитального движения (скорость этого движения  ~1 км/сек) за 11,8 млрд. лет. Естественно, что она упадет на Землю гораздо раньше полной потери энергии. Теперь становится понятным, почему у Меркурия и Венеры нет спутников, потеря энергии в их окрестностях так значительна, что длительное существование спутника невозможно. Луна существует в качестве спутника только за счет своих огромных размеров и сравнительно недавнего захвата Землей. У Марса и более далеких планет солнечная постоянная настолько мала, что довольно длительное существование спутников становится возможным.

Теперь посмотрим, как изложенные новые представления согласуются с практикой запуска искусственных спутников, т.е. с обратной ситуацией, когда тело m не сближается с М, а выбрасывается из него. Известно, См., например, Б.М. Яворский, А.А. Детлаф. Справочник по физике, “Наука”, М., 1964, стр. 79, что для того, чтобы m стало спутником М, ему надо сообщить первую космическую скорость:

                                        (21.25),

где R - радиус центрального тела. Для удаления m в бесконечность необходимо сообщить вторую космическую скорость (параболическую):

                                       (21.26).

На поверхности центрального тела, тело m обладает потенциальной энергией притяжения . Чтобы m оказалось в потенциальной яме на орбите вокруг центрального тела, очевидно (см. фиг. 21.2), что ему надо сообщить потенциальную энергию отталкивания , равную половине потенциальной энергии притяжения:

                                        (21.27).

Преобразуя (21.27), получим (21.25). Для того чтобы выбросить m на бесконечно большое расстояние (вторая космическая скорость), необходимо ему сообщить потенциальную энергию отталкивания, равную потенциальной энергии притяжения (чтобы общая энергия стала равной нулю):

                                        (21.28).

Из (21.28) найдем (21.26).

Таким образом, новая физика, солидаризируясь с официальной наукой в отношении выброса, о захвате имеет противоположные представления.

Из (21.4) найдем выражение для :

                                         (21.29).

Для Солнечной системы (21.29) будет иметь вид:

  см²/сек                              (21.30).

Зависимость  от целых чисел (квантованность значений ) представлена на фигуре 21.3.

Легко показать, что все планеты и спутники в Солнечной системе движутся с первой космической скоростью, соответствующей радиусу их орбиты. Для этого, например, подставим значение =V× r в (21.4) и получим (21.25). Учитывая (21.25) и что r= r₀×n² , легко получить соотношение: , которое показывает, что орбитальная скорость планет или спутников “земной” группы или “юпитерной” группы уменьшается по мере удаления от центрального тела в целое число раз относительно скорости в первом квантовом состоянии. Уменьшение центробежной скорости электрона при излучении фотонов и образовании атома также в целое число раз (формула (13.15)) указывает не только на родственные связи электростатического и гравитационного поля, но и на масштабную независимость их действия, т.е. общность законов макро- и микромира.

На фигуре 21.4 точками нанесены орбитальные скорости планет Солнечной системы и их спутников (по данным: Е.Н. Слюта и др. Сравнительная планетология, М., “Наука”, 1995) в зависимости от обратной величины их квантового числа. На основании вышеизложенного, каждая группа спутников должна расположиться на прямой, тангенс угла наклона которой численно равен орбитальной скорости члена этой группы в первом квантовом состоянии, т.е. V₀. Прямые проведены по ранее полученным значениям ₀ и r₀ для каждой группы, разделив одно на другое. Как видно, наблюдаемые скорости космических тел хорошо “легли” на прямые. Рядом с прямыми указано название групп, например: Солнце(з) - Земная группа планет, а Юпитер(ю) - спутники Юпитера “юпитерной” группы.

  Интересно рассмотреть численные значения V₀ :

Планета       V₀ км/сек      Планета        V₀ км/сек

Нептун(ю)    3,53             Нептун(з)     45,39

Юпитер(ю)    7,12            Юпитер(з)     68,13

Сатурн(ю)    16,52           Сатурн(з)     101,92

Солнце(ю)    27,80           Солнце(з)     146,14

Уран(ю)       34,69           Уран(з)        380,5

V₀ “юпитерных” и “земных” групп хотя и соответствуют друг другу, но неожиданно никак не кореллируют с массами их хозяев. Чтобы разобраться с этим интересным феноменом приведем значения квантовых чисел:

Планета       “юпитерные”           “земные”

Нептун         1,2                        4,5,6

Юпитер        1,2,3                     2,3,4,5,6

Солнце         2,3,4,5,6                3,4,5,6

Сатурн         2,3,4,5,10               5,6,7,8,9,10

Уран            4,5,6,7,9,11           35,36,37,38,39,40,41,42,43

За исключением Солнца, большие квантовые состояния соответствуют большим V₀, но на фиг. 20.4 максимумы на кривой распределения крупных комет и астероидов прослеживаются вплоть до квантового числа 10 для Земной группы (вертикальные тонкие стрелки), а квантовые числа Юпитерной группы вполне возможны до значений, больших 10 для еще не открытых “планет”. В этом случае Солнце в списке переместится ниже Сатурна, и последовательность будет полностью соответствовать последовательности для V₀. Включать Солнце в этот список не совсем корректно, но оправданием может служить глубокая уверенность в едином механизме образования космических систем.

Отсутствие корреляции между массой центральных космических тел и V₀ их спутниковых систем является дополнительным подтверждением того, что Солнечная система (как и другие звездные системы) образовалась за счет присоединения планет уже имеющих почти готовые спутниковые системы. Они формировались в межзвездной среде в различных условиях относительных скоростей центрального тела и пролетающих мимо потенциальных его спутников. Если их скорость относительно велика, то образовать систему могут только спутники с большими значениями квантового числа (как у Урана), если эта скорость мала, то систему образуют преимущественно тела с низкими значениями квантового числа (как у Нептуна). Очевидно, что последний случай более вероятен, поэтому низкие значения квантовых чисел наиболее часто встречаются. Поэтому все тела Солнечной системы, имеющие большие квантовые числа (например, кометы с большим эксцентриситетом), наверняка прибыли к нам издалека, а не из ближайшего межзвездного окружения Солнца. Это наиболее ярко демонстрирует нам Уран со своей спутниковой системой. Феномен Урана объяснить с ортодоксальных позиций практически невозможно.

Обратное вращение спутника или планеты доказывает его захват практически в целом виде. Происходит это следующим образом (фиг. 21.5 в виде «сверху» на плоскость Солнечной системы 1-1):

Левовинтовое тело m в направлении стрелки движется против часовой стрелки. Собственное его вращение происходит в ту же сторону, причем ось вращения параллельна оси винтовой траектории тела. После захвата тела, его орбита эволюционизирует таким образом, чтобы направление гравидинамического орбитального момента совпало с гравидинамическим моментом Солнечной системы в целом. Поскольку ось вращения тела сохраняет свое положение в пространстве, то в конце эволюции орбиты тело m будет двигаться в плоскости эклиптики в прямом направлении, но вращение вокруг собственной оси будет обратным. В процессе эволюции орбиты мы будем наблюдать сначала большой эксцентриситет и большое наклонение орбиты к плоскости эклиптики. Такие параметры мы наблюдаем у Плутона, следовательно, он сравнительно недавно захвачен Солнечной системой. Постепенно эти значения уменьшаются, но ось собственного вращения тела сохраняется в пространстве, поэтому захваченные тела с обратным вращением характеризуются большим наклонением экватора к плоскости орбиты. Этот угол зависит от угла между осью винтовой траектории тела до захвата и плоскостью Солнечной системы. Если этот угол близок к 90⁰ (фиг. 21.5а), то наклонение экватора будет близким к 180⁰, как у Венеры. Если этот угол близок к 0⁰ (фиг. 21.5b), то наклонение экватора к плоскости орбиты будет близким к 90⁰, и тело по орбите будет двигаться «лежа на боку», как Уран. Таким образом, обратное вращение планет или спутников указывает на захват этих тел целиком. Обращение многочисленных спутников Урана в его экваториальной плоскости в одну сторону особенно наглядно показывает, что Уран был захвачен вместе с собственной спутниковой системой, образованной в межзвездном пространстве.

Сравним изложенные представления с наблюдательными данными по выпадению на Землю метеоров. Если метеорное тело захвачено Солнечной системой из межзвездной среды с нулевой начальной скоростью, то оно будет двигаться (в конечном итоге) по круговой орбите вокруг Солнца. Если радиус орбиты соответствует земному, то скорость движения по орбите этого тела составит, как и у Земли, около 30 км/сек. В прямом направлении по этой орбите будет двигаться подавляющее большинство метеорных тел и лишь незначительное количество - в противоположном направлении. Очевидно, что скорость движения метеоров к Земле вдогонку будет нулевой, а навстречу 60 км/сек. Очевидно также, что скорость движения метеоров в межзвездной среде вблизи окрестностей Солнечной системы не может в точности равняться скорости движения Солнца по галактической орбите (250 км/сек), т.е. они имеют некоторую начальную скорость перед захватом. “Поскольку Солнечная система движется относительно межзвездной среды со скоростью 20-25 км/сек...”. Е.Н. Слюта и др., Сравнительная планетология, “Наука”, М., 1995, стр. 17.

 Мы можем найти, какая максимальная относительная скорость должна быть у межзвездного метеора, чтобы он был захвачен, например, на земную орбиту. Для этого приравняем его кинетическую энергию энергии связи по формуле (21.5):

                                    (21.31),

где r_з - радиус орбиты Земли.

Из (21.12): 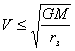                                                                   (21.32).

Формула (21.32) показывает, что на данную орбиту может быть захвачен межзвездный метеор, имеющий начальную скорость не более орбитальной (30 км/сек для земной орбиты), которая складывается с орбитальной. В этом случае орбита метеора будет эллиптической с эксцентриситетом близким к единице, если в (21.32) принять знак равенства. Таким образом, скорость падения на Землю метеоров уже принадлежащих (захваченных) Солнечной системе меняется от 0 до 30 км/сек, если метеоры движутся в прямом направлении и от 30 до 60 км/сек, если они движутся в обратном направлении (навстречу Земле). Если их скорость превышает 60 км/сек, то подобные метеоры, в зависимости от их скорости, могут быть захвачены на орбиту Венеры, Меркурия или гипотетических околосолнечных планет в 1 или 2 квантовом состоянии или их захват совсем невозможен. Для земной группы планет радиус орбиты первого квантового состояния равен 0,6213×10¹² см. Подставляя это значение в (21.32), найдем V=146 км/сек. В прямом направлении эти метеоры будут двигаться в верхних слоях атмосферы со скоростью 146 км/сек, а в обратном со скоростью 176 км/сек. Подобные метеоры следует считать транзитными путешественниками, поскольку они не способны к захвату и выпадение их на Землю следует считать случайным “прямым попаданием”. Ясно, что транзитные метеоры - это исключительно редкий случай, т.к. их относительная скорость сравнима с абсолютной скоростью Солнца, т.е. они являются гостями уже не межзвездной, а межгалактической среды. Вышеприведенные рассуждения полностью подтверждаются наблюдениями.

“Уипл сообщил об измерениях скоростей 144 метеоров. 15 из этих метеоров имели скорости немного больше 42 км/сек... Из 144 метеоров, наблюдавшихся Уиплом, ни в одном случае нельзя считать доказанным существование хотя бы одной подлинно гиперболической орбиты”. О. Струве и др., Элементарная астрономия, М., 1966, стр. 188.

“Случайно этот же метеорный поток дал возможность Хею, Парсонсу и Стюарту впервые определить скорости метеоров по гиперболическим отражениям (радиолокационный метод - В.К.). Они получили величину 22,9 км/сек, что хорошо согласуется с определенной из визуальных наблюдений величиной 23,7 км/сек.

Среди 11000 метеоров, зарегистрированных в течение 847 часов наблюдений с декабря 1948 г. по март 1950 г., Мак-Кинли нашел всего 32 метеора, скорости которых относительно Земли немного превышали 72 км/сек”. Там же, стр. 190.

Наиболее вероятно выпадение метеоритов на Землю в плоскости эклиптики “снаружи”, с противоположного от Солнца направления с запада на восток, т.е. вдогонку движению и вращению Земли. Поскольку ось вращения Земли наклонена к этой плоскости под углом 23,5⁰, то, в зависимости от времени года, выпадение метеоритов наиболее вероятно в полосе шириной от Южного тропика до Северного тропика. В этой связи представляет интерес гипотеза, высказанная моим старшим сыном о древней планетарной катастрофе в результате выпадения на Землю космического тела огромных размеров в район Филиппинского моря (вблизи Северного тропика, когда в северном полушарии была зима). В результате (см., например, Малый атлас мира, М., 1998, стр. 188-189) на Земле образовался грандиозный ударный кратер радиусом порядка 10000 км, охватывающий практически половину земного шара. Края кратера образовали Кордильеры в Северной Америке, Восточно-Тихоокеанское поднятие, Южно-Тихоокеанское поднятие, Австрало-Антарктическое поднятие и хребет Кергелен, Восточно-Индийский хребет. В противоположном удару направлении земная кора смялась с образованием горных систем Гималаи, Тибет, Тянь-Шань и горных хребтов Восточной Сибири. На дне кратера (большая часть Тихого океана) образовалась система радиальных разломов: Мендосино, Пионер, Меррей, Кларион, Клиппертон, Пасхи, Элтанин, а также радиально направленные системы тихоокеанских островов. Весь район падения стал с тех пор районом сейсмической и вулканической активности. Несомненно, что обломки земных пород при этом ударе попали не только на Луну, но и на Марс.

Здесь необходимо рассмотреть практически важную проблему устойчивости орбитального движения искусственных спутников Земли. Эта проблема актуальна из-за огромных затрат на их изготовление и запуск. Очевидно, что для обеспечения длительного и надежного функционирования искусственного спутника, его орбита и движение по орбите должны быть “естественными”, т.е. спутник должен находиться в одном из квантовых состояний, орбита должна лежать в плоскости эклиптики, движение должно быть прямым, а сам спутник (или его часть) вращаться в сторону движения. Все эти требования одновременно удовлетворить невозможно, но стремиться к этому нужно, если не хотим потерять спутник “по неизвестным причинам”.

Вековая загадка строения Солнечной системы решена.

Человечество много веков безуспешно пыталось понять, почему Солнечная система устроена так, а не иначе. Здесь эта проблема решена с чем я поздравляю человечество.

В главе 11.2.5 показано, что произведение Vr= для свободного космического тела определяется только его гравидинамическим самовоздействием и остается постоянным при орбитальном движении после захвата этого тела. Здесь мы воспользуемся формулой (11.2.5.12) и таблицей 11.2.5.1 из этой главы. Среднее («стандартное») значение /n 0,92×10¹⁹ см²/сек для планет земной группы. Среднее значение /n 4,82×10¹⁹ см²/сек для планет юпитерной группы. Тогда формулу (11.2.5.12) можно переписать так:

                                                              (21.33),

где  - «стандартное» значение . Подставив эти значения в (21.33) для земной и юпитерной группы, найдем радиусы орбит и, соответственно, орбитальные скорости в первом квантовом состоянии:

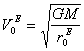,                                                    (21.34),

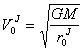,                                                    (21.35).

Подставляя численные значения в (21.34) и (21.35), получим:

=0,637×10¹² см, =14,44×10⁶ см/сек; =17,5×10¹² см, =2,75×10⁶ см/сек. Теперь можно подставить эти значения для расчета радиусов орбит и орбитальных скоростей планет земной и юпитерной группы:

r_E=0,637×10¹²×n², V_E=14,44×10⁶/n; r_J=17,5×10¹²×n², V_J=2,75×10⁶/n.   (21.36).                                                                                 

В таблице 21.1 представлены результаты теоретического расчета и реальных значений радиусов орбит и орбитальных скоростей планет.

Таблица 21.1.

Планета	Квантовое состояние	Среднее расстояние от Солнца, 10^12 см	Радиус орбиты вычисленный, 10^12 см	Средняя скорость орбитального движения, 10^6 см/сек	Орбитальная скорость, вычисленная, 10^6 см/сек
Меркурий	3	5,791	5,733	4,789	4,813
Венера	4	10,821	10,192	3,505	3,61
Земля	5	14,96	15,92	2,979	2,407
Марс	6	22,79	22,93	2,413	2,41
Юпитер	2	77,83	70	1,306	1,375
Сатурн	3	142,8	157,5	0,964	0,917
Уран	4	287,2	280	0,681	0,687
Нептун	5	449,8	437,5	0,543	0,55
Плутон	6	591	630	0,474	0,458

Хотя расчетные и наблюдаемые параметры планет отличаются, но следует иметь в виду, что эти параметры постепенно изменяются. Поэтому расчетные значения показывают будущие характеристики планет. Например, Земля со временем удалится от Солнца, примерно, на 10 миллионов километров, а Венера приблизится, примерно, на такую же величину.

Интересно узнать радиус винтовой траектории планеты в свободном состоянии до захвата. Очевидно, что он будет в n² больше ненешнего радиуса орбиты. Например, Земля имела радиус винтовой траектории в дальнем космосе в 25 раз больше ее орбитального радиуса. Некоторые тела Солнечной системы имеют квантовое число 10 и больше, следовательно, радиус их винтовой траектории в свободном состоянии в 100 и более раз превышал наблюдаемый.

Произведение Vr для планет порядка 10²⁰ см²/сек, а у спутников планет на 5 порядков меньше. Это означает только одно – положение спутников планет является результатом вторичного захвата. При первичном захвате космических тел Солнечной системой они распределяются, приблизительно, как планеты в соответствии со своей плотностью и квантовым состоянием. При этом имеют Vr приблизительно соответствующее ближайшей планете. Поскольку относительные скорости потенциальных спутников и планеты-хозяина невелики и, кроме того, они находятся близко друг к другу, то при вторичном захвате и образовании спутниковой системы Vr спутников будет на несколько порядков меньше. Таким образом, Солнечная система (как и любая другая звездная система) формируется за счет первичного захвата планет и вторичного захвата спутников. Механизм вторичного захвата полностью аналогичен первичному захвату, поэтому строение спутниковых систем повторяет строение Солнечной системы в миниатюре. Интересно отметить, что достаточно далеко расположенные от планеты тела имеют отрицательную относительную скорость (меньше скорости планеты), поэтому могут быть захвачены на спутниковую орбиту с обратным движением и вращением спутника.

В заключение этой главы можно посмеяться над ортодоксальными астрономами, которые недавно «запретили» Плутону называться планетой. К счастью, он об этом еще не знает.

Комментарии автора к главе 21:

1. Энергетический анализ захвата.

Я благодарен Сергею Алексееву за плодотворную дискуссию о проблеме захвата в результате которой я, наконец, сам понял суть этой проблемы. При бесконечном расстоянии между центральным и захватываемым телом энергия системы равна нулю. В процессе захвата захватываемое тело по спирали сближается с центральным телом. При этом сила притяжения обратно пропорциональна квадрату расстояния между телами из-за действия закона всемирного тяготения, а центробежная сила отталкивания обратно пропорциональна кубу расстояния между телами из-за действия закона сохранения момента импульса. В результате на некотором расстоянии от центрального тела эти силы уравновешиваются и захватываемое тело начинает двигаться по устойчивой круговой орбите, т.к. дальнейшее сближение тел становится невозможным. При этом половина полученной системой гравитационной энергии истрачена на отталкивание от центрального тела, а оставшаяся половина составляет энергию связи. В результате система в целом вновь имеет нулевую энергию, как и на бесконечном расстоянии. Если рассматривать энергию только захваченного тела, то его положительная энергия универсального отталкивания в точности равна отрицательной энергии связи, поэтому общая его энергия тоже нулевая. При обратном процессе удаления захваченного тела на бесконечность, мы преодолеем только отрицательную энергию связи, но такая же по величине положительная энергия универсального отталкивания будет способствовать удалению тела. Поэтому на бесконечности энергия системы снова станет нулевой.

Если захватываемое тело на бесконечности уже обладало некоторой положительной кинетической энергией (меньше глубины потенциальной ямы), то оно после захвата будет двигаться по эллиптической орбите с той избыточной энергией относительно равновесной, которой оно обладало на бесконечности.

2. Главная ошибка официальной космологии в проблеме захвата.

Официальная космология, пока, не имеет представления о винтовом движении любых свободных тел. Это достижение новой физики, которая утверждает, что все тела природы имеют собственный момент импульса, который сохраняется при их взаимодействии. Посмотрим на формулы (21.4) и (21.5). Из них видно, что потенциальная яма для захваченного тела образуется в любом случае. Если момент импульса этого тела большой, то устойчивая круговая орбита (дно потенциальной ямы) будет далеко от центрального тела, а энергия связи, соответственно, мала. И наоборот. Официальные представления исходят из того, что тело до захвата не обладает моментом импульса, т.е. движется прямолинейно к центральному телу. В этом случае захват невозможен, т.к. невозможно преобразование половины потенциальной энергии притяжения в энергию орбитального движения.

3. Физический смысл знаменитой формулы E=mc².

Все материальные тела состоят из «элементарных» частиц: электрона, протона, нейтрона и некоторых других. В разделе монографии «ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ» показано, что все они состоят из орбитального движения компонентов со скоростью света, которые удерживаются на круговой орбите гравидинамическим притяжением.Также в главе 1 вводится понятие универсальной энергии отталкивания, которую приобретает любое тело, двигающееся по окружности. Эта энергия численно равна «кинетической энергии» тела, но таковая фактически отсутствует до тех пор, пока тело не удалится по касательной к орбите. Посмотрите на фигуру 21.2. В применении к элементарным частицам и с учетом теоремы вириала здесь половина энергии  гравидинамического притяжения W_пр при образовании частицы расходуется на энергию связи компонентов (m_i c²/2), а вторая половина на энергию универсального отталкивания (m_i c²/2). Таким образом, чтобы удалить компоненты частицы на бесконечность и обратить энергию компонентов в нуль требуется затратить энергию E_i=m_ic². Общая энергия покоя (неподвижного) тела будет E₀=m₀c², а общая энергия движущегося тела E=mc², где m – релятивистская масса тела.

21.0.1 Эллиптические орбиты космических тел

Круговые орбиты космических тел являются исключительно редким случаем, когда избыточная энергия тела полностью исчерпана, но это может произойти только за бесконечное число оборотов по эллиптической орбите, когда на каждом обороте часть импульса тела передается системе в целом. Даже идеальная круговая орбита может исказиться под влиянием различных космических факторов: приливного воздействия соседей, выпадения на поверхность метеоритов и комет и т.п. Поэтому все космические тела находятся фактически в возбужденном состоянии, имея некоторую избыточную кинетическую энергию в сравнении с равновесным ее значением.

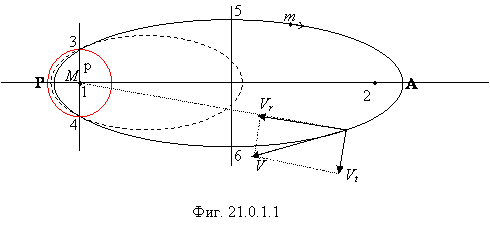
На фигуре 21.0.1.1 показана эллиптическая орбита тела m вращающегося по часовой стрелке вокруг массивного центрального тела M. Расстояние между точками P (перицентра) и A (апоцентра) орбиты равно большой оси эллиптической орбиты (2a), а расстояние между точками 5 и 6 – малой оси орбиты (2b). Расстояние между фокусами орбиты (точки 1 и 2) равно 2c. В процессе постепенной передачи импульса тела m системе в целом (фактически, телу M) происходит преобразование эллиптической орбиты в круговую (показана красным цветом), но при этом преобразовании все орбиты пересекаются в двух противоположных точках 3 и 4 на расстоянии радиуса будущей круговой орбиты – фокального параметра эллипса p (см. фигуру 13.2 в главе 13). Таким образом, эволюция эллиптической орбиты космического тела мало чем отличается от эволюции орбиты электрона в атоме. Исходные данные для последующего анализа мы определили.

Очевидно, что закон сохранения момента импульса требует, чтобы в любой точке орбиты в любое время вплоть до достижения круговой орбиты момент импульса L тела m относительно M сохранялся неизменным:

L=mV_t×r                                                                     (21.0.1.1),

где r – расстояние от m до M.

Несмотря на то, что на каждом обороте энергия тела m уменьшается, для одного оборота полную энергию этого тела в точках перицентра и апоцентра можно считать неизменной. Полная энергия складывается из универсальной энергии отталкивания (глава 1):

                                                           (21.0.1.2)

и энергии гравитационного притяжения к M:

                                                                         (21.0.1.3).

Поэтому полная энергия тела m будет:

                                                           (21.0.1.4).

Переписывая (21.0.1.4) для перицентра и апоцентра, приравнивая их между собой, после некоторых преобразований, получим:

                                                             (21.0.1.5),

откуда можно получить формулу для точного подсчета момента импульса тела m по положению перицентра и апоцентра его орбиты (или величины большой «a» и малой «b» полуоси эллипса):

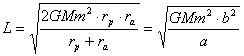                                (21.0.1.6).

Подставив в (21.0.1.6) численные данные для Земли (Е.Н. Слюта и др. Сравнительная планетология, М.,1995, стр. 78) найдем: L=25,974×10⁴⁶ г×см²/сек. Если воспользоваться (21.0.1.1) и подставить среднее расстояние от Солнца и среднюю орбитальную скорость Земли, то получим существенно отличающееся значение момента импульса Земли: L=26,632×10⁴⁶ г×см²/сек.

Если мы найдем минимум функции (21.0.1.4), то получим, что при этом скорость тела m будет равна первой космической скорости:

                                                                      (21.0.1.7),

а само тело займет круговую орбиту. Если мы сделаем то же самое для расстояния перицентра любой эллиптической орбиты, то легко найти отношение энергии тела на этой орбите (E) радиуса r к энергии тела на круговой орбите (E₀) радиуса r₀:

                                                                          (21.0.1.8).

Для параболической орбиты расстояние перицентра в два раза меньше радиуса круговой орбиты (фокального параметра), поэтому энергия такого тела вдвое превышает энергию на стационарной орбите.

По отношению радиуса круговой орбиты (фокального параметра) к перигелийному расстоянию r можно найти эксцентриситет данной орбиты:

                                                                         (21.0.1.9).

Сравнивая 21.0.1.8 и 21.0.1.9, мы можем записать другое выражение для отношения энергии тела на эллиптической орбите к энергии на круговой орбите, выраженное через эксцентриситет орбиты, который можно определить более точно:

                                                                       (21.0.1.10).

Эксцентриситет земной орбиты в настоящее время 0,0167, поэтому энергия Земли на эллиптической орбите превышает ее энергию в равновесном состоянии в  1,0167 раза.

Учитывая, что:

                                                                 (21.0.1.11),

где p – фокальный параметр, а e – эксцентриситет орбиты, можно посчитать момент импульса тела или радиус равновесной орбиты, зная эти величины.

Остальные подробности о движении тел по эллиптическим орбитам можно прочесть в главе 21.

Комментарии автора к главе 21.0.1:

1. Энергия связи электрона и космических тел на эллиптических орбитах.

Поскольку электростатическое и гравитационное взаимодействие не имеют существенных отличий, для дальнейшего воспользуемся данными таблицы 13.1. Большая ось орбиты (2a) равна сумме расстояний до перицентра и апоцентра, выраженных через относительные единицы r₀ (радиус круговой орбиты):

n/(n+1)+n/(n-1)=2/(1-1/n²)=2a                               (1).

Но 1-1/n²=E_tie                                              (2),

Где E_tie – энергия связи на данной орбите с центральным телом. Подставив (2) в (1), найдем: 1/E_tie=a или, переходя к абсолютным величинам: E₀/E_tie=a/r₀ , откуда:

E_tie=(E₀×r₀)/a                                             (3).

Энергия связи на любой эллиптической орбите оказывается обратно пропорциональной большой полуоси этой орбиты, т.к. произведение E₀×r₀ для всех орбит одинаково.

21.1. Что провоцирует землетрясения

Когда мы рассматривали орбитальное движение электрона в водородоподобном атоме, мы выяснили, что эллиптические орбиты пересекаются с параболической орбитой и круговой орбитой в двух противоположных точках на расстоянии фокального параметра от главного фокуса орбиты. В этих точках составляющая скорости, направленная к фокусу или от фокуса принимает максимальное значение. Эта составляющая равна нулю для строго круговой орбиты и в точках перигелия и афелия орбиты Земли. Производя те же математические манипуляции, которые мы делали при выводе центробежной скорости для электрона в водородоподобном атоме и учитывая формулы, приведенные в таблице 13.1, можно записать:

                                           (21.1.1),

где: e – эксцентриситет земной орбиты (e=0,0167) а  – энергия связи Земли и Солнца, если Земля имела бы круговую орбиту:

                                            (21.1.2).

Получена аналогично формуле (2.4), G – гравитационная постоянная, m – масса Земли, M – масса Солнца, - произведение средней орбитальной скорости Земли на среднее расстояние от Солнца. Подставив (21.1.2) в (21.1.1), найдем значение E_св=2,651386∙10⁴⁰ эрг, а E_св0 =2,652129∙10⁴⁰ эрг. Понятно, что реальная энергия связи Земли с Солнцем меньше из-за некоторой избыточной механической энергии Земли, вызывающей не круговую, а эллиптическую орбиту. Эту избыточную энергию можно считать как:

                                               (21.1.3),

где V_c – скорость, направленная по радиусу-вектору к главному фокусу. Численное значение этой скорости из (21.1.3) равно 499 м/сек или, примерно, 0,5 км/сек.

Таким образом, на каждом обороте вокруг Солнца в перигелии (3-4 января) и в афелии  (в начале июля) составляющие скорости, направленные к Солнцу и от Солнца равны нулю. В начале апреля Земля проходит одну точку фокального параметра и составляющая скорости от Солнца максимальна, а в начале октября эта составляющая направлена к Солнцу и тоже максимальна. Учитывая, что ядро Земли обладает колоссальной инерцией и, как желток в яйце, покоится в магме, то при разгоне и торможении оно пытается отстать или, наоборот, по инерции продолжает двигаться к Солнцу. При этом оно вызывает деформацию земных оболочек и провоцирует сброс предыдущих напряжений земной коры или создание новых. Учитывая, что после прохождения перигелия скорость до 0,5 км/сек нарастает быстрее, весенние землетрясения на Земле должны приводить к более сильным катастрофам, чем осенние. Кроме того, описанное явление способствует активизации вулканической деятельности.

 Особенно сильно описанный эффект должен наблюдаться у Меркурия с большим эксцентриситетом орбиты, а также у спутников планет с большими эксцентриситетами.

Влияние приливов.

Кроме инерционного движения ядра Земли в этом движении участвуют все подвижные оболочки: атмосфера, гидросфера и земная кора. На эти движения также накладывается приливное воздействие Солнца и Луны. Если приливные движения атмосферы и гидросферы практически не оставляют последствий в напряженных состояниях земной коры, а влияют только на океанские и атмосферные течения, то приливные движения самой земной коры не остаются без последствий в смысле провоцирования землетрясений. Таким образом, можно сделать вывод, что приливное воздействие усиливает провокацию землетрясений в апреле в ночное время, когда Земля удаляется от Солнца и в октябре в дневное время, когда Земля приближается к Солнцу и инерция проявляется в наибольшей степени.

21.2. Траектории тел при захвате и гигантские атомы

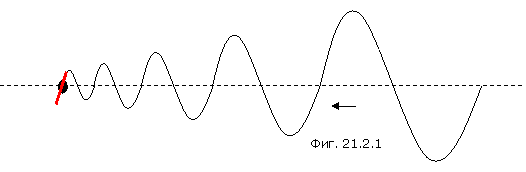
В монографии показано, что все свободные тела двигаются по винтовой траектории. Это относится, как к телам микромира, так и макромира. Поскольку электростатическое взаимодействие аналогично гравитационному взаимодействию из-за одинакового вида формул закона всемирного тяготения и закона Кулона, для определенности, мы будем рассматривать здесь гравитационное взаимодействие, показанное на фигуре 21.2.1.

Траектория захватываемого тела показана с направления, перпендикулярного оси винтовой линии. По мере приближения к центральному телу радиус винтовой траектории уменьшается, а скорости тангенциального и поступательного движения увеличиваются. При этом сами эти скорости остаются равными друг другу. В конечном итоге тело оказывается захваченным на круговую орбиту с параметрами:

                                                                             (21.2.1),

где: r₀ – радиус орбиты, =Vr, где V – тангенциальная скорость на витке винтовой траектории тела, r – радиус витка, M – масса центрального тела. Энергия связи с центральным телом W₀ выражается формулой:

                                                                          (21.2.2),

где: G – гравитационная постоянная, m – масса захватываемого тела.

Из фигуры 21.2.1 понятно, что ортодоксы, пока, не представляют реальной траектории тела при захвате.

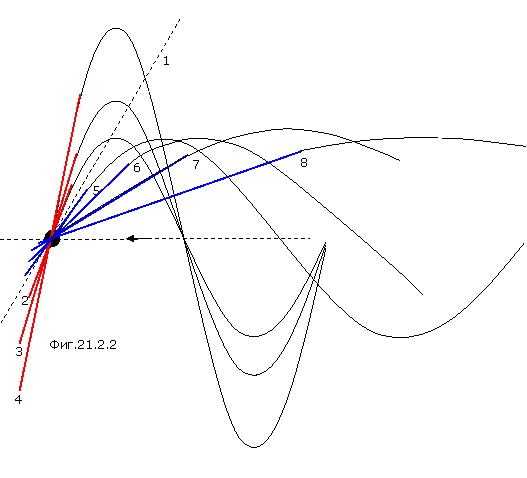
На фигуре 21.2.2 представлены траектории тел на последнем витке перед захватом. Цифрой 1 показано направление, составляющее с направлением оси винтовой траектории угол =45⁰. Все тела, имеющие на бесконечности нулевую поступательную скорость после захвата, образуют круговую орбиту, плоскость которой наклонена на угол больше 45⁰ к оси винтовой траектории. С увеличением тангенциальной скорости на бесконечности (увеличением ) этот угол растет, также растет радиус круговой орбиты в соответствии с формулой (21.2.1). Эти траектории обозначены красным цветом (2,3,4). Если при той же тангенциальной скорости увеличивать поступательную скорость тела на бесконечности, то после захвата возникает эллиптическая орбита, эксцентриситет которой пропорционален поступательной (кинетической) энергии тела на бесконечности. Плоскость эллиптической орбиты составляет с осью винтовой траектории угол меньше 45⁰. Эти траектории обозначены синим цветом (5,6,7,8). Если эта энергия равна глубине потенциальной ямы в соответствии с формулой (21.2.2), то эксцентриситет становится равным единице и захват невозможен. Захватываемое тело по параболической траектории вновь удаляется в бесконечность.

Захват, показанный на фигуре 21.2.1 назовем жестким захватом. При таком захвате радиус круговой траектории минимален, а энергия связи с центральным телом максимальна. С увеличением  радиус круговой траектории увеличивается, а энергия связи с центральным телом уменьшается. Такой захват назовем мягким захватом.

Гигантские атомы.

Анализ различных вариантов гравитационного захвата позволяет с успехом перенести выводы этого анализа на захват электрона атомом. В частности, нас будет интересовать мягкий электронный захват. Представьте себе, что мы не позволяем атому захватить электрон вариантом жесткого захвата, при котором за счет электростатического притяжения электрона к положительному иону винтовая траектория электрона значительно уменьшается в размерах. Если реализовать мягкий захват, то возможно получение  гигантских известных атомов. Эти атомы, имея размеры от нормальных до ридберговских атомов, будут стабильны в отличие от последних потому, что валентные электроны в них имеют единственное значение момента импульса , а не кратное, как в ридберговских атомах, от которого избавляются при любой возможности. Для реализации мягкого захвата электронов необходимо их придерживать внешним электрическим полем, которое ускоряет положительный ион и тормозит электрон. Если подобрать соответствующие начальные скорости ионов и электронов, то мягкий захват можно осуществить при минимальной скорости сближения электрона с ионом. При этом радиус винтовой траектории электрона будет таким же большим, как у свободного теплового электрона, соответственно, радиус круговой орбиты захваченного электрона будет таким же большим. В химическом отношении представляет интерес производство гигантских атомов, у которых все валентные электроны захвачены посредством мягкого захвата.

Производство гигантских атомов и синтез из них гигантских молекул открывает поистине сказочные перспективы перед химией, медициной, биологией и технологией. Возможность получения любых заданных параметров орбит захваченных электронов безгранично расширяет эти перспективы.

Рассмотрим, в качестве примера, работу энергетического аккумулятора на основе гигантских молекул водорода. Предположим, что сосуд емкостью 100 литров заполнен таким водородом при нормальных условиях. При некотором небольшом нагреве части газа гигантские молекулы водорода начнут диссоциировать на гигантские атомы водорода, а последние ионизироваться, распадаясь на протоны и электроны. Электроны пустим во внешнюю электрическую цепь и возвращаем в сосуд, где они вновь соединяются с протонами с образованием уже обычного атомарного водорода, который превратится в нормальный молекулярный водород. Во всех описанных процессах энергия выделяется за исключением незначительного начального теплового импульса для запуска. Интересно посчитать запас энергии в подобном энергетическом аккумуляторе. Пренебрежем выделившейся электрической энергией и тепловой энергией в реакции превращения атомарного водорода в молекулярный. Будем считать, что эту энергию мы истратили на управление тепловым режимом установки, т.к. она очень напоминает ядерный реактор и потенциально способна привести к мощному тепловому взрыву. В 100 л содержится 100:22,4=4,5 моля газа, или 4,5×6×10²³×2=0,54×10²⁵ атомов. При каждом взаимодействии протона с электроном с образованием нормального атома водорода выделяется 13,6 эв энергии. Общее выделение энергии в этом процессе составит 13,6×0,54×10²⁵ эв или количество энергии эквивалентное сжиганию 280 литров бензина (а вес водорода в сосуде всего 9 грамм). Таким образом, энергетический аккумулятор преобразует «гигантский» водород в обыкновенный в экологически чистом процессе. Естественно, что полученную энергию на заводе по производству гигантских атомов придется затратить.

В герметичном сосуде, наполненном гигантскими молекулами водорода при большом давлении под действием электрической искры происходит мгновенное преобразование гигантского водорода в нормальный с таким выделением энергии, которое недоступно при использовании любых известных взрывчатых веществ.

В принципе, любые гигантские атомы можно использовать для сварки, резки и плавления любых веществ, в том числе, и в космических условиях.

21.3. Энергетический баланс при изменении орбиты спутника

Эта глава написана с целью помочь читателям яснее понять, что происходит при попытке изменить орбиту спутника.

Из равенства силы притяжения спутника к центральному телу и центробежной силы для любой равновесной круговой орбиты справедлива формула:

                                                         (21.3.1),

где: V – орбитальная скорость, G – гравитационная постоянная, M – масса центрального тела, r – радиус орбиты.

Умножим обе части (21.3.1) на m/2, где m – масса спутника:

                                                      (21.3.2).

Левая часть уравнения (21.3.2) представляет собой потенциальную энергию универсального отталкивания (глава 1), поэтому удобно записать (21.3.2) для низкой орбиты 1 и высокой орбиты 2 и найти разницу универсальной энергии отталкивания  E_rep для этих орбит:

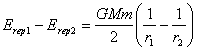                                           (21.3.3).

Уравнение (21.3.3) показывает, что разница в энергиях отталкивания для двух орбит составляет ровно половину разницы энергии притяжения к центральному телу. По теореме вириала для устойчивой динамической системы потенциальная энергия притяжения равна сумме потенциальной энергии отталкивания и такой же энергии связи. Следовательно, вторая половина изменения энергии притяжения в (21.3.3) тратится на изменение энергии связи спутника с центральным телом. При переходе спутника с низкой орбиты на высокую пропорционально уменьшается «кинетическая» энергия спутника (энергия универсального отталкивания), уменьшается энергия связи его с центральным телом и потенциальная энергия притяжения к центральному телу. Закон сохранения энергии требует, чтобы эти потери были полностью скомпенсированы добавкой «кинетической» энергии спутнику для перевода его на более высокую орбиту. Здесь возникает кажущийся парадокс: мы должны разогнать спутник, чтобы уменьшить его орбитальную скорость на более высокой орбите. При этом затраченная энергия не только полностью компенсируется, но и часть используется за счет первоначальной скорости. Для перевода спутника с высокой орбиты на более низкую нужно произвести соответствующее торможение и снова возникает кажущийся парадокс: мы уменьшили орбитальную скорость, а она, в итоге, увеличилась на низкой орбите.

Здесь необходимо добавить уточнение. При добавлении скорости спутнику на орбите 1, он начинает двигаться по эллиптической орбите с перицентром в точке добавленной скорости, обладая избыточной энергией. При движении от перицентра к апоцентру орбиты изменения энергии будут соответствовать вышеизложенным. Если мы хотим, чтобы орбита 2 спутника стала круговой, нам нужно добавить в точке апоцентра такую скорость, чтобы она полностью соответствовала формуле (21.3.1)