20. ОБРАЗОВАНИЕ И СТРОЕНИЕ СОЛНЕЧНОЙ СИСТЕМЫ
Применим изложенные представления для космических масштабов. Для этого немного преобразуем формулу (2.3) к виду:
![]() (20.1).
(20.1).
Общее строение Солнечной системы наглядно демонстрирует нам проявление гравидинамического взаимодействия: все планеты вращаются по орбитам и вокруг собственных осей в одну сторону - сторону вращения Солнца в одной плоскости. То же самое происходит и со спутниками планет. Особенно наглядно это видно у быстро вращающегося Юпитера, имеющего к тому же и большую массу, следовательно, мощное гравидинамическое поле, заставляющее не только саму орбиту Юпитера лежать в плоскости Солнечной системы, но его самого иметь минимальное наклонение экватора к орбите, а также заставляющее спутники Юпитера следовать примеру хозяина, за исключением внешних спутников с которыми разберемся позднее.
“Обращаясь к Солнечной системе, нетрудно обнаружить следующие существенные особенности ее строения:
1. Все планеты обращаются вокруг Солнца в одном и том же направлении.
2. Все планеты вращаются вокруг своих осей в направлении, соответствующем направлению их обращения вокруг Солнца (исключение составляют Уран и Венера).
3. Эксцентриситеты орбит планет очень мало отличаются от нуля, т.е. орбиты планет почти круговые. Исключение представляют орбиты Меркурия и Плутона.
4. Орбиты планет, кроме Меркурия и Плутона, лежат почти в одной плоскости, мало наклоненной к плоскости солнечного экватора.
5. Крайне неравномерно распределяется между Солнцем и планетами момент количества движения (для точки массы m, обращающейся по окружности радиуса r со скоростью v, момент количества движения равен mvr). На долю Солнца, в котором сосредоточено 99% всей массы Солнечной системы, приходится только 2% ее полного момента количества движения.
6. Вращение Солнца вокруг его оси происходит в ту же сторону, в какую движутся планеты вокруг Солнца.
7. Орбиты большинства спутников планет близки к круговым, а движения большинства спутников по их орбитам происходят в том же направлении, в каком планеты движутся вокруг Солнца.
8. Орбиты спутников в большинстве своем мало наклонены к плоскостям экваторов своих планет.
9. Планеты делятся на две группы: планеты типа Земли и планеты-гиганты типа Юпитера. Планеты с большей массой вращаются вокруг своих осей с меньшими периодами. Планеты-гиганты имеют наименьшую плотность.
Ни одной из существовавших и существующих космогонических гипотез не удается убедительно объяснить эти закономерности и особенности, и это обстоятельство порождает скептическое отношение к этим гипотезам”. В.Г. Демин “Судьба Солнечной системы”, “Наука”, М., 1975, стр.61.
Известно, что в нашей Галактике, как и в других, имеется и сейчас достаточное количество протонов, электронов, отдельных атомов, молекул, пылевых частиц, более крупных тел, вплоть до огромных кусков вещества в виде астероидов, комет и т.п. “Межпланетная пыль - частицы преимущественно с массой 10-3 - 10-5 г., распространенные в межпланетном пространстве. Общая масса межпланетной пыли оценивается в 1019 - 1020 г. При удалении от Солнца плотность пылевого облака падает примерно как R -1,3 , а на расстояниях ~3 а.е. пыль практически отсутствует. Наибольшая концентрация межпланетной пыли наблюдается в области эклиптики, поскольку у большинства частиц наклонение орбит не превосходит 30-400”. Е.Н. Слюта и др. “Сравнительная планетология”, “Наука”, М., 1995, стр.42.
Согласно гипотезе образования гравидинамического поля, не только элементарные частицы или молекулы в свободном состоянии движутся по винтовой линии, но и любые другие тела. Некоторым подтверждением могут служить винтовые формы хвостов комет I типа. (Е.Н. Слюта и др. “Сравнительная планетология”, “Наука”, М., 1995, стр.71). При этом наступает равновесное состояние, когда сила, аналогичная силе Лоренца в электродинамике исполняет роль силы, притягивающей тело к оси винтовой линии, а об универсальной отталкивательной энергии и соответствующей силе мы уже вели речь. Такое движение тела будет устойчивым, т.к. оно находится в потенциальной яме. В любом случае гравидинамическое поле заставляет свободное тело двигаться по правовинтовой или левовинтовой линии и первый закон Ньютона, выходит, неверен по отношению к свободному телу, а справедлив лишь к оси винтовой траектории его. Поэтому мы во Вселенной не должны встречать ни одного тела, движущегося строго прямолинейно, или строго по параболической или гиперболической траектории. Против этого астрономы, кажется, не возражают.
Здесь нужно предостеречь от неосторожного обращения с формулой де
Бройля ![]() , определяющей "длину волны" частиц
с моментом импульса
, определяющей "длину волны" частиц
с моментом импульса ![]() . Обычно, в ее знаменатель подставляют какую
заблагорассудится массу, получают умопомрачительно короткую волну для макротел
(что фактически означает невероятно большую энергию при мизерной скорости
движения) и на этом основании считают, что макротела не обладают волновыми
свойствами. Если в новой физике волна де Бройля имеет совершенно ясный
физический смысл и является поперечной (“колебания” частицы при движении по
винтовой линии происходят поперек ее перемещения в пространстве), то
ортодоксальная наука в этом вопросе не имеет ясных представлений. Если считать
волну де Бройля поперечной, то приходится принять на вооружение эфир со
свойствами твердого тела, чтобы обеспечивалось распространение такой волны.
Если считать ее продольной, то эфир должен обладать свойствами жидкости или
газа. Если отказаться от эфира вообще, то приходится вводить новый вид волны -
“волна вероятности”, но тогда нужно раскрыть ее физический смысл и показать
теоретически, что такая волна должна обладать свойствами обычных волн, что
доказано экспериментально. Даже в виде волнового пакета частицу невозможно
представить, т.к. по представлениям официальной физики для волн де Бройля
существует дисперсия даже в вакууме, поэтому волновой пакет расплывается со
временем. “Это не позволяет представлять частицы в виде группы волн де Бройля”
(Б.М. Яворский, А.А. Детлаф, Справочник по физике, “Наука”, М., 1964, стр.
644).
. Обычно, в ее знаменатель подставляют какую
заблагорассудится массу, получают умопомрачительно короткую волну для макротел
(что фактически означает невероятно большую энергию при мизерной скорости
движения) и на этом основании считают, что макротела не обладают волновыми
свойствами. Если в новой физике волна де Бройля имеет совершенно ясный
физический смысл и является поперечной (“колебания” частицы при движении по
винтовой линии происходят поперек ее перемещения в пространстве), то
ортодоксальная наука в этом вопросе не имеет ясных представлений. Если считать
волну де Бройля поперечной, то приходится принять на вооружение эфир со
свойствами твердого тела, чтобы обеспечивалось распространение такой волны.
Если считать ее продольной, то эфир должен обладать свойствами жидкости или
газа. Если отказаться от эфира вообще, то приходится вводить новый вид волны -
“волна вероятности”, но тогда нужно раскрыть ее физический смысл и показать
теоретически, что такая волна должна обладать свойствами обычных волн, что
доказано экспериментально. Даже в виде волнового пакета частицу невозможно
представить, т.к. по представлениям официальной физики для волн де Бройля
существует дисперсия даже в вакууме, поэтому волновой пакет расплывается со
временем. “Это не позволяет представлять частицы в виде группы волн де Бройля”
(Б.М. Яворский, А.А. Детлаф, Справочник по физике, “Наука”, М., 1964, стр.
644).
Алогичность рассуждений официальной физики в трактовке формулы де
Бройля очевидна. Из-за того, что волна имеет очень малую длину или, наоборот,
очень большую, еще не следует, что ее совсем нет. Правильное толкование состоит
в том, что сама формула де Бройля есть результат гравидинамического
самовоздействия частиц с моментом импульса ![]() и при других
значениях этого момента будет несправедливой. А что касается массы частицы в ее
знаменателе, то это такое же недоразумение, являющееся следствием
догматического отношения к математике на фоне недопонимания физической
сущности, как и масса электрона, стоящая в знаменателе формулы, выражающей
радиус орбиты электрона в современной теории атома. Записывая формулу де Бройля:
и при других
значениях этого момента будет несправедливой. А что касается массы частицы в ее
знаменателе, то это такое же недоразумение, являющееся следствием
догматического отношения к математике на фоне недопонимания физической
сущности, как и масса электрона, стоящая в знаменателе формулы, выражающей
радиус орбиты электрона в современной теории атома. Записывая формулу де Бройля:
![]() ,
где Vп -
поступательная скорость частицы, разделим обе части на 2
,
где Vп -
поступательная скорость частицы, разделим обе части на 2![]() :
: ![]() , но
, но ![]() =mVТ×r (где VТ -
тангенциальная скорость) и является моментом количества движения частицы. Спрашивается,
где? Ведь частица свободна. Ответ однозначен - на витках винтовой линии, если
не хотим вращать электрон со сверхсветовой скоростью или вовсе лишить
физического смысла момент импульса. Подставив значение
=mVТ×r (где VТ -
тангенциальная скорость) и является моментом количества движения частицы. Спрашивается,
где? Ведь частица свободна. Ответ однозначен - на витках винтовой линии, если
не хотим вращать электрон со сверхсветовой скоростью или вовсе лишить
физического смысла момент импульса. Подставив значение ![]() , найдем:
, найдем: ![]() . VT придется
принять равным Vп,
чтобы снова остаться в рамках здравого смысла при изменениях Vп и имея
в виду принцип равного распределения энергии по степеням свободы, тогда
получаем:
. VT придется
принять равным Vп,
чтобы снова остаться в рамках здравого смысла при изменениях Vп и имея
в виду принцип равного распределения энергии по степеням свободы, тогда
получаем: ![]() . Мы получили результат, показывающий, что
длина волны де Бройля, начиная от микрочастиц и кончая астрономическими объектами
равна длине орбиты этой частицы в связанном состоянии или длине окружности
поперечного сечения винтовой линии в свободном состоянии, причем последняя
величина значительно превышает первую, в чем можно убедиться на примере
свободного и связанного электрона. Этот вывод подтверждает единую физическую
основу движения любых свободных тел и единство законов микро- и макромира. В
единстве этих законов у нас еще будет возможность неоднократно убедиться.
. Мы получили результат, показывающий, что
длина волны де Бройля, начиная от микрочастиц и кончая астрономическими объектами
равна длине орбиты этой частицы в связанном состоянии или длине окружности
поперечного сечения винтовой линии в свободном состоянии, причем последняя
величина значительно превышает первую, в чем можно убедиться на примере
свободного и связанного электрона. Этот вывод подтверждает единую физическую
основу движения любых свободных тел и единство законов микро- и макромира. В
единстве этих законов у нас еще будет возможность неоднократно убедиться.
Поскольку физический смысл длины волны де Бройля стал тривиальным, в дальнейшем, употребляя этот термин, мы не будем вкладывать в него больше того, что в нем содержится, исходя из вышеизложенного, а уж тем более не будем считать частицы волной, хотя их движение и обладает некоторыми свойствами волны из-за винтовой траектории.
Теперь мы сможем утверждать, что свободные тела микро- и макрокосмоса, двигаясь по винтовым линиям, демонстрируют нам нарушение сразу двух законов Ньютона: они не движутся прямолинейно и действие не равно противодействию. Во всяком случае, законы Ньютона требуют уточнения формулировок. Относительно второго закона Ньютона можно сказать следующее. В тиши кабинета можно считать, как это и принято, что на тело, движущееся по окружности, действует центростремительная сила, вызывающая центростремительное ускорение в соответствии со вторым законом Ньютона, а центробежная сила действует на "связь". Придется закрыть глаза на то обстоятельство, что “связь” под действием неуравновешенной силы должна двигаться с ускорением от центра вращения. Однако, перевернувшись на крутом повороте вместе со своим автомобилем, мы будем твердо убеждены в том, что на нас действовала именно центробежная сила, и все было хорошо до тех пор, пока она была равна центростремительной, обусловленной реакцией опоры. Поэтому правильное толкование этого вопроса будет таким. Если тело устойчиво движется по окружности, то оно находится в потенциальной яме и сила притяжения к центру окружности равна силе отталкивания. Обе силы приложены к движущемуся телу. Сумма этих сил равна нулю и по второму закону Ньютона ускорение отсутствует. В такой интерпретации все случаи движения тел по окружности становятся совершенно ясными. По представлениям современной науки потенциальной ямы не существует ни в случае движения электрона вокруг ядра, ни в случае движения космического тела вокруг центрального. Поэтому данные системы должны быть принципиально неустойчивы, а их фактическая устойчивость (являющаяся образцом устойчивости в нашем мире) однозначно указывает на ошибочность этих представлений. Только понятие универсальной энергии отталкивания, введенное новой физикой, позволяет дать исчерпывающее решение этой проблемы.
Гравидинамическое поле, как и магнитное, короткодействующее, радиус его
действия по порядку величины сравним с радиусом частицы в случае ее вращения
вокруг оси и сравним с радиусом орбиты, по которой течет "гравитационный
ток". В последнем случае индукция гравидинамического поля максимальна
вблизи движущегося тела, поэтому на расстояниях, значительно превышающих
размеры тел, гравидинамическое поле не может быть конкурентом гравитационного
поля притяжения в случае космических объектов или электростатического поля в
случае движения электронов в атоме. Вместе с тем, задавая начальный момент
количества движения по винтовой линии свободной частице, оно полностью
определяет положение орбиты этой частицы в связанном состоянии, оставляя на
долю дальнодействующих гравитационного и электростатического поля черновую
работу по удержанию тела на предопределенной заранее орбите. Радиус ее из
бесконечного набора разрешаемых потенциальной энергией притяжения и
универсального отталкивания выбирается именно гравидинамическим полем. Ниже мы
увидим, что эта гениальная выдумка Создателя (автор имеет собственного царя в
голове, поэтому является убежденным атеистом и упоминание всуе имени бога
служит только для удобочитаемости текста), когда вид Вселенной определяется не
мощным гравитационным, а пренебрежимо более слабым, в данных условиях,
гравидинамическим полем, позволила создать живой, эволюционизирующий, развивающийся
мир, вместо мертвого и неподвижного, поскольку диссипации энергии в макромире
невозможно избежать в отличие от микромира. Таким образом, в космосе мы имеем
широкий набор "длин волн де Бройля" начиная от тех, что определяются
его формулой и справедливой для частиц с механическим моментом ![]() и
кончая макротелами "длина волны" которых может значительно превышать
размеры Солнечной системы вплоть до галактических размеров. Двигаясь по
винтовой линии, макротела с определенным значением Vr, которое определяет будущее их
положение в Солнечной системе независимо от массы, "одеваются" на
Солнечную систему, уменьшая при этом радиус движения и увеличивая орбитальную
скорость в соответствии с законом сохранения момента количества движения.
Основная масса вещества поступает в Солнечную систему из области галактической
"орбиты" Солнца (кавычки станут ясны позднее, когда выяснится, что
орбиты как таковой нет) точно так же, как на планеты в основном вещество
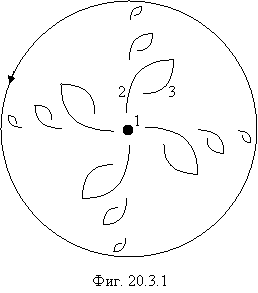
поступает с планетарной орбиты. Этот наиболее распространенный случай изображен
на фигуре 20.1.
и
кончая макротелами "длина волны" которых может значительно превышать
размеры Солнечной системы вплоть до галактических размеров. Двигаясь по
винтовой линии, макротела с определенным значением Vr, которое определяет будущее их
положение в Солнечной системе независимо от массы, "одеваются" на
Солнечную систему, уменьшая при этом радиус движения и увеличивая орбитальную
скорость в соответствии с законом сохранения момента количества движения.
Основная масса вещества поступает в Солнечную систему из области галактической
"орбиты" Солнца (кавычки станут ясны позднее, когда выяснится, что
орбиты как таковой нет) точно так же, как на планеты в основном вещество
поступает с планетарной орбиты. Этот наиболее распространенный случай изображен
на фигуре 20.1.
|
|
|
|
|
|
Вы скажите, что автор рассматривает надуманную проблему. Что-то не очень заметно, чтобы из космоса к нам поступало значительное количество вещества. На это можно ответить просто - его обязательно найдут, и если сегодняшнее его поступление окажется малым, то это вполне компенсируется прошлым изобилием и будущим поступлением. Естественно, что в прошлом поступление вещества в Солнечную систему было значительно больше. “Бомбардировка метеоритная интенсивная - событие, следы которого сохранились в геологической истории планетных тел и малых тел Солнечной системы в виде областей с высокой плотностью кратеров ударных на твердой поверхности. Определения возраста абсолютного пород лунных материков датируют резкий спад интенсивной метеоритной бомбардировки временем ~3,9 млрд. лет назад. Начало ее, вероятно, смыкается с последними стадиями аккреции (рост тел за счет присоединения новых частиц - В.К.) планетных тел (~4,6 млрд. лет назад)”. Е.Н. Слюта и др. “Сравнительная планетология”, “Наука”, М., 1995, стр.11.
Автор надеется, что и читатель будет разделять его оптимизм в этом вопросе, закончив чтение этой главы.
Макротела, достигая радиуса действия гравидинамического поля Солнечной системы в целом, сравнимого с размерами системы, разворачивают вектор своего механического момента таким образом, чтобы занять параположение в Солнечной системе, при этом не имеет значения правовинтовое или левовинтовое направление движения имело макротело и с какой стороны плоскости Солнечной системы оно появилось. В других случаях вещество может поступать с направлений, перпендикулярных плоскости Солнечной системы. Последние исследования антарктических метеоритов подтверждают, что метеориты, поступающие на Землю с этих двух направлений, различаются между собой: “Метеориты антарктические - метеориты, найденные в Антарктиде, где в определенных геоморфологических условиях в результате интенсивного испарения притекающих с большой площади масс льда происходит накопление метеоритов на поверхности льда. Найдено более 10 000 образцов, в том числе новые (например, метеориты лунные) и редкие типы. По соотношениям метеоритов разных классов, а также по некоторым химическим особенностям популяция метеоритов антарктических отличается от неантарктических. Причина этого пока неизвестна”. Е.Н. Слюта и др. “Сравнительная планетология”, “Наука”, М., 1995, стр.43.
|
|
|
|
|
|
При этом могут быть два варианта, изображенные на фигуре 20.2.
В варианте 20.2а тело с правовинтовым движением входит в Солнечную систему, двигаясь внутри ее в направлении движения планет (собственное вращение его происходит в ту же сторону). В варианте 20.2б тело с левовинтовым движением при подходе к Солнечной системе чуть притормаживается из-за взаимного отталкивания разноименных гравидинамических полюсов, поэтому занимает положение на периферии Солнечной системы или спутниковой системы планеты, демонстрируя обратное движение. Для спутников планет Солнечной системы картина движений строительного материала подобна, только значение Vr, соответственно, меньше.
Исходя из наблюдаемого строения Солнечной системы, можно сделать вывод о том, что за Плутоном мы сможем обнаружить небольшие спутники Солнца с обратным движением. Кроме того, правовинтовых тел из северной части неба и левовинтовых из южной части неба в Солнечной системе наблюдается очень мало, так как они должны двигаться против вращения нашей Галактики в целом. Эти тела можно считать временно «аномальными» в отличие от «нормальных», соответствующих вариантов фигуры 20.2а.
Кометы (начиная от пылинок кометного состава и кончая большими кометами), являющиеся основным поставщиком вещества в Солнечную систему убедительно демонстрируют нам правильность изложенных представлений, причем очевидно, что кометы группы 2 недавно захвачены Солнечной системой, а кометы группы 1 - давно и практически перешли в стационарное состояние (как позднее увидим, относительное). “Случайное накопление возмущений за счет сил тяготения планет называется диффузией комет. К.А. Штейнс указал три закона диффузии.
|
|
|
|
|
|
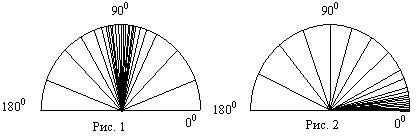
Согласно первому закону диффузии накопление случайных возмущений в движении комет приводит к постепенному уменьшению наклонов плоскостей орбит комет к плоскости эклиптики. На рис. 1 указано распределение орбит по их наклонам к эклиптике для вновь открываемых комет, а на рис. 2 приведено распределение старых комет по наклонам их орбит к плоскости эклиптики.
Как видно, для новых орбит равновероятны как прямые, так и обратные движения, в то время, как большинство остальных (старых - В.К.) комет движется вокруг Солнца в прямом направлении.
По второму закону диффузии накопление возмущающих эффектов приводит к тому, что орбиты с большими перигелийными расстояниями имеют в среднем меньшие эксцентриситеты и меньшие значения больших полуосей.
Второй закон диффузии находится в очень хорошем согласии с данными наблюдений всех комет, которые были открыты и наблюдались после 1700 г. Он характеризует направление эволюции кометных орбит под действием планетных возмущений.
Третий закон диффузии объясняет распределение орбит новых комет в пространстве и формулируется следующим образом: количество наблюдаемых новых комет возрастает с уменьшением перигелийного расстояния. Он находит простое объяснение: кометы с большими перигелийными расстояниями разрушаются намного медленнее, нежели те кометы, которые в перигелии проходят очень близко к Солнцу”. В.Г. Демин “Судьба Солнечной системы”, “Наука”, М., 1975, стр.140-142.
С точки зрения новой физики, все три закона диффузии комет и не только их, но и любого тела в Солнечной системе можно объединить в один. Любое тело в Солнечной системе, не поглощенное другими телами, за счет гравидинамического взаимодействия с системой стремится занять круговую орбиту с прямым движением (против часовой стрелки, если смотреть с северного полюса мира) и собственным вращением в ту же сторону. Этому способствуют взаимодействие с другими телами Солнечной системы и диссипативные процессы. В результате достигается минимум потенциальной энергии системы в целом. Рисунок 1 подтверждает, что “новые” кометы Солнце захватывает на своей галактической орбите, поэтому наклонение их орбит близко к 900 (см. фигуру 20.1). Законы диффузии комет станут значительно яснее после ознакомления с теорией захвата космических тел.
Особенно наглядно видна эволюция орбит в Солнечной системе на примере семейств комет Нептуна, Урана, Сатурна и Юпитера. Если в семействе Нептуна орбиты комет обладают большим эксцентриситетом, большим наклоном орбит и часто обратным движением, то в семействе Юпитера характерны близость плоскостей орбит комет к плоскости эклиптики и исключительно прямые обращения вокруг Солнца с малым эксцентриситетом (см. Е.Н. Слюта и др. “Сравнительная планетология”, “Наука”, М., 1995, стр.62-63).
Несмотря на то, что рост членов Солнечной системы за счет метеоритного вещества не столь велик, как из кометного, к нему полностью относится все, что выше было сказано о кометах. “Подсистема астероидов плоская - астероиды с наклонением орбиты меньше 80, т.е. с орбитами, расположенными вблизи плоскости эклиптики. Подсистема охватывает около половины всех астероидов... (Сравни с рис.1 и рис.2 - В.К.). Подсистема астероидов сферическая - астероиды с наклонением орбиты больше 80”. Е.Н. Слюта и др. “Сравнительная планетология”, “Наука”, М., 1995, стр.52.
Точно так же, как мы находили выражение (2.3) для радиуса орбиты электрона в атоме, мы можем найти и выражение для радиуса орбиты планеты, находящейся в потенциальной яме при движении вокруг Солнца (официальная наука не знает о существовании потенциальной ямы в данном случае):
![]() (20.2).
(20.2).
Это положение макротело, попавшее в Солнечную систему, занимает достаточно быстро, т.к. гравитационное взаимодействие намного сильнее гравидинамического в этих условиях. Поскольку образование атома принципиально не отличается от образования Солнечной системы, аналогично (20.1) можем записать:
![]() (20.3),
(20.3),
где: ![]() = Vr -
произведение тангенциальной скорости по винтовой линии и радиуса ее для
свободного макротела, которое сохраняется и в образованных такими телами
планетах и их спутниках, т.к.:
= Vr -
произведение тангенциальной скорости по винтовой линии и радиуса ее для
свободного макротела, которое сохраняется и в образованных такими телами
планетах и их спутниках, т.к.:
![]() (20.4).
(20.4).
G - гравитационная постоянная, r - радиус орбиты планеты,
m - ее масса, М - масса Солнца (или центрального тела, например,
планеты для ее спутников). Кстати, из (20.3) легко получается третий закон
Кеплера, а само выражение (20.3) равносильно формуле первой космической
скорости для тела, движущегося по орбите радиуса r. Подставив ![]() =
Vr и
=
Vr и ![]() , где Т - период обращения, в (20.3),
после простых преобразований найдем:
, где Т - период обращения, в (20.3),
после простых преобразований найдем: ![]() , а это и есть третий закон
Кеплера. Обратите внимание, что при этом выводе мы совершенно не пользовались
понятием центростремительного ускорения, как это сделано, например, в книге: Дж.
Орир “Популярная физика”, “Мир”, М., 1969, стр.107-108.
, а это и есть третий закон
Кеплера. Обратите внимание, что при этом выводе мы совершенно не пользовались
понятием центростремительного ускорения, как это сделано, например, в книге: Дж.
Орир “Популярная физика”, “Мир”, М., 1969, стр.107-108.
Построив график, на оси ординат которого отложены значения произведений
орбитальной скорости планеты на радиус ее орбиты, а на оси абсцисс ![]() ,
получим прямую линию, исходящую из начала координат с тангенсом угла наклона
равным
,
получим прямую линию, исходящую из начала координат с тангенсом угла наклона
равным ![]() . Этот факт, подтверждающий верность (20.3)
служит очень серьезным аргументом в пользу вышеизложенных рассуждений,
прекрасно объясняет распределение механического момента в Солнечной системе,
(официальная наука не может это объяснить) и говорит о том, что нет
необходимости Солнечной системе "рождаться", как нечто целое. “Некоторые,
например, крупный английский астроном Ф. Хойл, придерживаются мнения об
одновременном образовании Солнца и планет из первичного облака. Но на этом пути
возникают затруднения в объяснении распределения момента количества движения
(количества вращения) между Солнцем и планетами (в Солнечной системе на долю
планет приходится 98% момента вращения, хотя они составляют лишь 0,1% массы
Солнечной системы”. К.П. Белов, Н.Г. Бочкарев “Магнетизм на Земле и в космосе”,
“Наука”, М., 1983, стр.168), т.е. “неудовлетворительно объясняются трудности,
оказавшиеся роковыми для гипотезы Лапласа”. В.Г. Демин “Судьба Солнечной
системы”, “Наука”, М., 1975, стр.63.
. Этот факт, подтверждающий верность (20.3)
служит очень серьезным аргументом в пользу вышеизложенных рассуждений,
прекрасно объясняет распределение механического момента в Солнечной системе,
(официальная наука не может это объяснить) и говорит о том, что нет
необходимости Солнечной системе "рождаться", как нечто целое. “Некоторые,
например, крупный английский астроном Ф. Хойл, придерживаются мнения об
одновременном образовании Солнца и планет из первичного облака. Но на этом пути
возникают затруднения в объяснении распределения момента количества движения
(количества вращения) между Солнцем и планетами (в Солнечной системе на долю
планет приходится 98% момента вращения, хотя они составляют лишь 0,1% массы
Солнечной системы”. К.П. Белов, Н.Г. Бочкарев “Магнетизм на Земле и в космосе”,
“Наука”, М., 1983, стр.168), т.е. “неудовлетворительно объясняются трудности,
оказавшиеся роковыми для гипотезы Лапласа”. В.Г. Демин “Судьба Солнечной
системы”, “Наука”, М., 1975, стр.63.
“Иными словами, удельный (на единицу массы) момент количества движения у планет больше, чем у Солнца, в среднем в 35 000 раз. Это обстоятельство являлось непреодолимым препятствием для многих космогонических гипотез. В новейших гипотезах принимается, что за перенос момента количества движения в Солнечной системе ответственно магнитное поле Солнца”. Физика космоса, “Советская энциклопедия”, М., 1976, стр.70. Читателю, видимо, ясно, что привлечение магнитного поля Солнца связано с совершенной безвыходностью положения ортодоксальной науки в этом вопросе. Момент количества движения планеты и их спутники приносят с собой при захвате их солнечной системой целиком или в большей их части.
Тут надо обратить внимание на то, что ортодоксальная наука даже не рассматривала вариант зарождения Солнечной системы по механизму постепенного роста за счет внешнего материала. Любая достаточно большая масса, способная удерживать материал за счет гравитационного поля, будь то звезда или холодное тело, с неизбежностью (см. главу о захвате космических тел) будут образовывать планетную систему, собирая всякий хлам, которого предостаточно в космическом пространстве. “Действительно, начиная с 1973 г., появляются все новые указания на присутствие межзвездных пылинок в веществе метеоритов”. Физика космоса, “Советская энциклопедия”, М., 1976, стр. 443.
Поэтому Солнечная система не "родилась", а зародилась в виде маленьких тел в заранее определенных местах, когда Солнце еще не было звездой (см. ниже о Юпитере), которые росли вместе с Солнцем и продолжают расти за счет космического вещества. В этом смысле, планетная система Солнца старше самого Солнца в качестве звезды. Возраст большинства метеоритов близок возрасту Солнечной системы и составляет ~4,6 млрд. лет. Е.Н. Слюта и др., Сравнительная планетология, “Наука”, М., 1995, стр.14. Возраст Земли и Луны определен таким же значением. Эти факты говорят о том, что вещество в ближайших окрестностях во Вселенной в виде космических тел появилось около 5 млрд. лет назад.
Явление зодиакального света и противосияния в плоскости эклиптики подтверждают этот вывод. “...советский астроном В.Г. Фесенков показал, что материя зодиакального света должна обновляться через каждые 100 000 лет. За указанное время все пылинки, образующие зодиакальное облако, должны выпадать на Солнце вследствие эффекта Пойнтинга - Робертсона. Источник, пополняющий убыль материи зодиакального облака, с достоверностью пока не установлен”. Физика космоса, “Советская энциклопедия”, М., 1976, стр. 78. Далее мы узнаем откуда берется материал для формирования космических тел.
Для того чтобы в этом убедиться еще раз, достаточно взглянуть на "лицо" планет земной группы, испещренных метеоритными кратерами или заглянуть в историю Земли, для чего приходится лезть глубоко под землю и чем дальше, тем глубже. Кстати, как будет ясно из дальнейшего, метеориты не могут попадать на планеты юпитерной группы в таком количестве, как на планеты земной группы, а кометы - наоборот.
С одним и тем же значением Vr могут быть макротела любой массы и любой поступательной скорости. Они, попадая в Солнечную систему, располагаются на орбите соответствующей планеты или спутника и подпитывают их веществом. Макротела с другими значениями Vr не могут усваиваться данной планетой или спутником и у них единственный путь к усвоению данным космическим телом - изменить соответствующим образом Vr в результате возмущений и диссипации энергии, в противном случае это макротело станет добычей другой планеты или спутника. Этот вывод не совсем верен, в дальнейшем мы убедимся в том, что макротела и микрочастицы не образуют непрерывной последовательности моментов количества движения в результате "интерференции", поэтому "неправильных" космических объектов крайне мало. Таким образом, Солнечная система, подобно атому, освещаемому фотонами разной длиной волны, также "освещается" макротелами с разной длиной волны де Бройля и поглощает только избранные макротела. В отличие от атома, это поглощение необратимо и приводит к непрерывному росту массы системы. На этом аналогии макро- и микромира далеко не исчерпываются.
Обращая внимание на физические свойства материала, из которого строятся
планеты, мы сразу замечаем два вида его: основная масса, поставляемая кометами,
представляет собой материал, плотность которого, примерно, в 5 раз ниже
плотности материала метеоритов. Следовательно, a первого,
грубо говоря, должно быть в 5 раз больше второго. При одной и той же скорости
вращения, частица малой плотности создает меньшую напряженность
гравидинамического поля, что приведет при одной и той же тангенциальной
скорости винтового движения к существенному увеличению радиуса винтовой линии
из-за слабой силы Лоренца (для гравидинамического поля). Поэтому макротела
вещества комет наращивают в Солнечной системе планеты юпитерной группы, а
вещества метеоритов - планеты земной группы в соответствии с распределением
вещества в космическом пространстве, которое и определяет относительную массу
планет. При этом метеоритное вещество располагается ближе к центральному телу,
как для планет, так и для их спутников, чем кометное вещество. Естественно, что
плотность вещества в каждой комете и метеорите непостоянны и изменяются в некоторых
не перекрывающих друг друга пределах, но, как указывалось выше, планеты будут
поглощать не всевозможные значения ![]() внутри этих пределов,
а только избранные, соответствующие данной планете или спутнику. Таким образом,
космическое вещество, прежде чем попасть на планету, сепарируется по плотности
и, следовательно, химсоставу. Конечно, в целом, мы наблюдаем усредненную
картину, но в продолжение определенного периода, прохождение Солнечной системой
по галактическому пути вызывает преимущественный рост самого Солнца, если по
пути попадают облака водорода, планет земной или юпитерной группы, если по пути
попадает соответствующий материал. “Но тогда должен существовать постоянный
источник, питающий скопления космической материи”. В.Г. Демин “Судьба Солнечной
системы”, “Наука”, М., 1975, стр.121.
внутри этих пределов,
а только избранные, соответствующие данной планете или спутнику. Таким образом,
космическое вещество, прежде чем попасть на планету, сепарируется по плотности
и, следовательно, химсоставу. Конечно, в целом, мы наблюдаем усредненную
картину, но в продолжение определенного периода, прохождение Солнечной системой
по галактическому пути вызывает преимущественный рост самого Солнца, если по
пути попадают облака водорода, планет земной или юпитерной группы, если по пути
попадает соответствующий материал. “Но тогда должен существовать постоянный
источник, питающий скопления космической материи”. В.Г. Демин “Судьба Солнечной
системы”, “Наука”, М., 1975, стр.121.
“Переменность тяготения тел Солнечной системы в некоторой степени зависит также от процессов роста массы планет вследствие постоянного выпадения на них метеорного вещества. В движении самих планет этот эффект не вызовет сколько-нибудь заметных изменений, однако этого нельзя утверждать относительно движения спутников планет на космогонических интервалах времени”. (Там же, стр.180).
“Мы упомянули еще один эффект, могущий оказать влияние на эволюцию спутниковых движений, а именно, эффект роста массы планет за счет выпадения метеорной материи. Этот эффект в наше время весьма невелик, ибо, например, Земля за счет падения метеорной материи каждый год увеличивает свою массу примерно на 3-6 тыс. т, однако он сказывается на движении Луны. Если бы количество метеорной материи в Солнечной системе не пополнялось, то влиянием незначительного роста масс планет можно было бы пренебречь. К сожалению, этого нельзя утверждать. Существует гипотеза, согласно которой ледниковые периоды на Земле повторяются с периодичностью порядка 200 млн. лет. Геологические данные не противоречат этой гипотезе. ... Как известно, в Галактике наблюдаются в значительных количествах протяженные газово-пылевые облака. Солнечная система, проходя через эти облака, пополняет запасы метеорного вещества”. (Там же, стр.184).
“Помимо тормозящего эффекта космической пыли, на тела Солнечной системы воздействует и солнечная радиация, которая порождает не только световое давление, но и вызывает дополнительное (радиативное) торможение. Последнее особенно сильно проявляется в движении малых тел, в частности, метеорной пыли. В этом направлении важные исследования были проведены академиком В.Г. Фесенковым. Приведем некоторые из его результатов. Радиативное торможение приводит к уменьшению размеров орбит. Так, для частицы радиусом в 1 см с плотностью в 3 г/см3 , первоначально двигавшейся по орбите с большой полуосью в 2 а.е., время падения на Солнце составляет около 60 млн. лет. Для микрометеоритов радиусом в 10 мк с плотностью в 1 г/см3 , движущихся в окрестности земной орбиты, время падения на Солнце составляет всего 7000 лет. Отсюда следует, что межпланетное пространство должно постепенно “очищаться” от космической пыли (а масса Солнца расти! - В.К.), если не будет происходить компенсация ее пополнением из каких-либо других источников”. (Там же, стр.186-187).
В результате всех этих рассуждений мы приходим к удивительному выводу о "квантовых" состояниях планет и их спутников в Солнечной системе и в любых других космических системах. Правда, этот вывод содержится в известном эмпирическом правиле Боде для радиусов орбит планет, поэтому вызывает удивление не формальная, а реальная квантованность, вернее даже, общность микро- и макромира. “Радиусы планетных орбит приблизительно подчиняются найденному из наблюдений закону Боде - Тициуса: Rn = (0,3×2n-2 + 0,4) а.е., где n - номер планеты. Эта формула, справедливая и для планет-гигантов, если считать Юпитер не пятой, а шестой планетой, стимулировала в свое время поиски пятой планеты. На ее месте было открыто кольцо астероидов (при n=5, R=2,8 а.е.)”. Физика космоса, “Советская энциклопедия”, М., 1976, стр. 70.
Несколько цитат по поводу поиска квантовых состояний планет в ранней и современной астрономии из: В.Г. Демин “Судьба Солнечной системы”, “Наука”, М., 1975, стр.235-237.
“Если проследить за эволюцией взглядов ученых, то можно заметить, что еще с древних времен философы, физики, а позднее и механики отдавали приоритет идее об определенной “организации” Солнечной системы. Так, Платон выдвинул принцип “идеальности” небесных движений, согласно которому небесные движения должны быть равномерными и круговыми. ... В природе действительно чаще всего мы встречаемся с почти круговыми движениями. С другой стороны, принцип Платона заставляет задумываться над вопросом: “А не “выбирают” ли планеты свои орбиты по какому-либо неизвестному еще физическому принципу?” (Такой принцип и предлагает новая физика - В.К.). В течение двух последних веков, начиная от Тициуса и Боде, не один астроном пытался найти закон планетных расстояний. Эти попытки не прекращаются и сейчас (достаточно вспомнить закон планетных расстояний О.Ю. Шмидта). И несмотря на эмпиризм и слепой поиск, несмотря на отсутствие физических и механических руководящих идей, сами эти поиски не оцениваются нами как поиски философского камня. Почему бы и в самом деле не существовать закону планетных расстояний? Могут ли планеты двигаться “на каких попало” орбитах? Не обязаны ли они в своем выборе орбит подчиняться каким-то правилам?... Хотя силы ядерного взаимодействия отличны от сил гравитационного взаимодействия, все же поиски принципов “квантования” орбит планет кажутся вполне естественными.... Оказывается, непреодолимого барьера между классической и квантовой механикой нет. Это особенно ясно показал член-корр. АН СССР Н.Г. Четаев. Он неоднократно высказывал интереснейшую мысль, оставшуюся, к сожалению, без внимания: “Устойчивость, явление принципиально общее, как-то должна, по-видимому, проявляться в основных законах природы”.... Результат Четаева поразителен. Правило отбора устойчивых действительных движений в гамильтоновых системах совпадает с правилами квантования орбит электронов: оно приводит к фундаментальному для современной физики уравнению Шредингера”.
Придется снова обратиться к атому водорода и провести некоторые сравнения с Солнечной системой. Большая ошибка Бора и его современных последователей, как нами показано ранее, состоит в том, что они предполагают возможность существования у электрона кратных значений момента количества движения, несмотря на то, что закон сохранения момента количества движения это категорически запрещает. Если кратность момента импульса для электрона в атоме невозможна (за исключением ридберговских атомов), то это вполне естественное состояние для космического объекта, поскольку формула (20.4) справедлива не только для тела, растущего из космического материала, но и для самого этого материала. В этом смысле, как это не парадоксально, теория атома Бора больше справедлива для Солнечной системы, чем для атома. Поэтому радиус орбиты космического тела будет (из теории Бора):
r=r0n2 (20.5),
если не учитывать эллиптические орбиты или “преобразовать” их в круговые (см. ниже), где: r - радиус орбиты планеты, а r0 - радиус орбиты планеты в основном состоянии, n - квантовое число Бора (не путать с квантовыми числами в теории атома, изложенной выше). Переписав (20.5) в виде:
![]() (20.6)
(20.6)
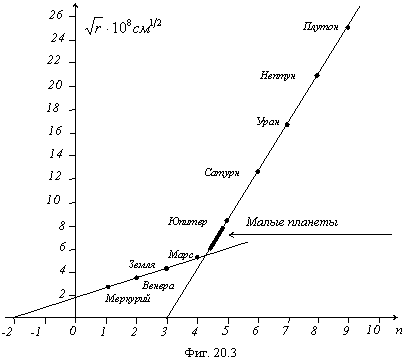
и отложив на оси ординат ![]() для планет Солнечной системы, а на оси
абсцисс целые числа, увидим, что планеты земной группы, и планеты группы
Юпитера образуют две пересекающиеся прямые (фиг. 20.3).
для планет Солнечной системы, а на оси
абсцисс целые числа, увидим, что планеты земной группы, и планеты группы
Юпитера образуют две пересекающиеся прямые (фиг. 20.3).
Из фигуры 20.3 можно найти:
Для земной группы: r0=0,6213×1012 см. Меркурий n=3, Венера n=4, Земля n=5, Марс n=6.
Для группы Юпитера: r0=17,16×1012 см. Юпитер n=2, Сатурн n=3, Уран n=4, Нептун n=5, Плутон n=6.
Интересно отметить, что для планет земной группы не отмечается планет с n=1 и n=2, а для группы Юпитера нет планеты с n=1. Отсутствие их, с одной стороны, объяснимо тем, что планета в основном состоянии находится слишком близко к центральному телу и разрушается от приливного воздействия его. С другой стороны, планеты земной группы с n=1 и 2 настолько близко должны быть расположены у Солнца, что, несмотря на термостойкий материал, собирающийся в этой области, в условиях вакуума, он легко испаряется. То же можно сказать и о планете 1 группы Юпитера, которая должна находиться между Землей и Марсом, поскольку вещество комет в этих условиях также не термостойко. Однако поступает в Солнечную систему кометного вещества значительно больше, чем метеоритного, поэтому надо рассматривать не статическое, а динамическое равновесие. Если поступление вещества превышает его испарение, то масса растет, в обратном случае - уменьшается. Примером последнего служит Уран, который в процессе поворачивания своей орбиты в плоскость Солнечной системы вместе со своими спутниками практически не потреблял вещество, но терял его, поэтому масса планеты "выпадает" из ряда масс планет группы Юпитера. В любом случае от комет остается более термостойкий "мусор", который при распаде кометного вещества приобретает квантовое число 1,5 и уже не может дойти до места назначения в планету 1 юпитерной группы, поэтому между Марсом и Юпитером в виде пояса малых планет (наружного кольца Солнца) идет сортировка вещества. Там же находятся и “планеты” земной группы с квантовыми числами выше 6.
Таблица 13.1 теперь нам пригодится для того, чтобы посчитать квантовые состояния членов Солнечной системы с большими эксцентриситетами орбит. Очевидно, что космическое тело не может занять дно потенциальной ямы испусканием порций энергии, как это способен делать электрон. Максимальная энергия связи с центральным телом (минимум потенциальной энергии) достигается постепенным рассеиванием избыточной энергии космического тела (которую легко найти, пользуясь формулами таблицы 13.1) за счет диссипативных процессов (сопротивление движению космической среды, приливное воздействие, возмущение орбиты от влияния других тел и т.п.). В таких условиях целочисленного изменения квантового числа n ждать не приходится. Случайным образом ориентированная в пространстве эллиптическая орбита космического тела, попавшего в Солнечную систему, постепенно без скачков переходит в круговую в плоскости эклиптики с прямым движением по орбите (против часовой стрелки, если смотреть с северного полюса мира). Это относится к любым макротелам от пылинок до планетного масштаба, поэтому падение микрометеорита на Луну или захват Солнечной системой Урана вместе со всеми его спутниками - суть один и тот же процесс поглощения системой макротел, потенциально давно готовых к захвату еще в межзвездной и межгалактической среде из-за винтового движения их. “Четыре внешних спутника Юпитера обладают обратным движением. Объяснить происхождение всех спутников, как с прямым, так и с обратным движениями в едином процессе очень трудно. Разумно поэтому поставить вопрос: а не приобретены ли спутники с обратным движением Юпитером потом, “по случаю”? Не остался ли надолго в окрестностях Юпитера случайно “забредший” в его сферу действия астероид? Такое явление небесные механики называют захватом. Астрономы, мало знакомые с небесной механикой, считают возможность захвата вполне вероятной. Однако доказать строго математически возможность и большую или достаточно заметную вероятность захвата совсем не просто. Пока мы не имеем ее надежных количественных оценок. (Они даны ниже в этой книге - В.К.). Поэтому правильнее воздержаться от ответа на этот вопрос”. В.Г. Демин “Судьба Солнечной системы”, “Наука”, М., 1975, стр.126-127. Очевидно, что новая небесная механика, утверждая движение макротел по винтовой траектории и существование потенциальной ямы при гравитационном взаимодействии, одновременно утверждает не только вероятность, но и неизбежность захвата, теория которого будет дана позднее.
Однако существует другого рода квантованность - по значениям
произведения Vr. В атоме такая квантованность невозможна, т.к. момент
импульса электрона ![]() сохраняет свое значение, следовательно,
произведение
сохраняет свое значение, следовательно,
произведение ![]() =Vr есть величина постоянная (для
нерелятивистских электронов). В космическом пространстве идет процесс
интенсивного роста макротел. При этом слипаться будут частицы, имеющие
одинаковые параметры винтовой траектории, поскольку они имеют возможность
достаточно долго находиться рядом. Подобная “интерференция волн де Бройля”
макротел приводит к тому, что произведение Vr любого макротела имеет не
какие попало, а некоторые квантованные значения. Очевидно, что Vr будет
определяться не массой, а плотностью макротел, т.к. при малой плотности
гравидинамическое поле частицы будет малым, следовательно, аналог силы Лоренца
невелик и витки винтовой линии будут иметь очень большие размеры (Vr
велико). Если мы мысленно предотвратим поступление нового вещества в Солнечную
систему, то, набравшись терпения, дождемся, что орбиты всех членов Солнечной
системы станут круговыми. Поэтому расчеты лучше вести для “идеальных” -
круговых орбит, которые неизбежны для стационарного состояния и приобретение
такой формы орбит космических объектов - вопрос только времени. Для планет, их
спутников и большинства астероидов это не имеет большого значения, т.к. их
орбиты уже близки к круговым, а для комет экстраполяция их орбит в будущее совершенно
необходима, иначе с ними не разобраться.
=Vr есть величина постоянная (для
нерелятивистских электронов). В космическом пространстве идет процесс
интенсивного роста макротел. При этом слипаться будут частицы, имеющие
одинаковые параметры винтовой траектории, поскольку они имеют возможность
достаточно долго находиться рядом. Подобная “интерференция волн де Бройля”
макротел приводит к тому, что произведение Vr любого макротела имеет не
какие попало, а некоторые квантованные значения. Очевидно, что Vr будет
определяться не массой, а плотностью макротел, т.к. при малой плотности
гравидинамическое поле частицы будет малым, следовательно, аналог силы Лоренца
невелик и витки винтовой линии будут иметь очень большие размеры (Vr
велико). Если мы мысленно предотвратим поступление нового вещества в Солнечную
систему, то, набравшись терпения, дождемся, что орбиты всех членов Солнечной
системы станут круговыми. Поэтому расчеты лучше вести для “идеальных” -
круговых орбит, которые неизбежны для стационарного состояния и приобретение
такой формы орбит космических объектов - вопрос только времени. Для планет, их
спутников и большинства астероидов это не имеет большого значения, т.к. их
орбиты уже близки к круговым, а для комет экстраполяция их орбит в будущее совершенно
необходима, иначе с ними не разобраться.
Учитывая вышеизложенное, воспользуемся из таблицы 13.1 соотношением:
![]() (20.7),
(20.7),
где rp - перигелийное расстояние, r0 - радиус круговой орбиты. Чтобы избавиться от n, из этой же таблицы воспользуемся соотношением:
![]() (20.8),
(20.8),
где e - эксцентриситет орбиты. Подставив (20.8) в (20.7), найдем, каков будет радиус круговой орбиты по наблюдаемому перигелийному расстоянию и эксцентриситету орбиты:
r0=rp(1+e) (20.9).
|
|
|
|
|
|
Можно было и прямо воспользоваться формулой (13.19), чтобы получить (20.9), но физический смысл (20.9) остался бы не совсем ясен.
Воспользовавшись данными: Е.Н. Слюта и др. “Сравнительная планетология”, “Наука”, 1995, стр.91-105, по формуле (20.9) рассчитаем будущее положение круговых орбит астероидов (диаметром больше 100 км) и известных комет. Результаты представлены на фигуре 20.4. Из фигуры видно, что как кометы, так и астероиды соберутся вместе на расстоянии 2-3 а.е. от Солнца, т.е. в поясе малых планет. Здесь скоро будут все кометы группы 1, к тому времени стабилизируются и кометы группы 2 и т.д. Поэтому в поясе малых планет мы имеем возможность наблюдать внутреннее вещество комет. Многие исследователи считают кометы одними из самых древних реликтовых тел Солнечной системы, другие предполагают, что некоторые кометы приходят к нам из других планетных систем. Известный голландский астроном Я. Оорт предполагает существование на окраинах Солнечной системы (150 000 а.е.) облака комет, питающего Солнечную систему. Предполагают также, что кроме облака Оорта (в существовании которого мало кто сомневается) есть еще один резервуар комет - пояс Уиппла, который находится за орбитой Нептуна. “Число комет в этой области оценивается в 109 с суммарной массой ~1027 г. Предположение основывается на заметных возмущениях в движении Нептуна”. Е.Н. Слюта и др. “Сравнительная планетология”, “Наука”, М., 1995, стр.58.
В непосредственной близости от Земли окажутся “наши” кометы: Галлея, Брорзена, Брорзена-Меткофа и Хонда-Мркоса-Пайдушаковой. Все они с неизбежностью упадут на Землю или некоторые из них на Луну, которая сама обязательно упадет на Землю (см. ниже). Поэтому, выпадение космических тел на поверхность планет и их спутников является не случайным событием, как его трактует официальная наука, а закономерным, в связи с чем космическое патрулирование совершенно необходимо для безопасности человечества.
Планета 2 земной группы тоже должна зарождаться, хотя и менее интенсивно, из-за относительного дефицита метеоритного вещества, поэтому на ее месте вполне вероятно нахождение "зародыша" из особо плотных и термостойких веществ. Более вероятно наличие колец вокруг Солнца, аналогичных кольцам планет юпитерной группы. “Неоднократно высказывалось предположение, что десятая планета Солнечной системы движется внутри орбиты Меркурия. К такому выводу в результате расчетов возмущенного движения Меркурия пришли астрономы Морской обсерватории в Вашингтоне”. В.Г. Демин “Судьба Солнечной системы”, “Наука”, М., 1975, стр.54.
Что касается планет с квантовым числом больше 6, то можно сказать следующее. Если и возможно существование планет прогрессивно уменьшающейся массы с квантовыми числами 7, 8, 9, 10 для земной группы планет, то эти планеты точно попадают в пояс малых планет в такой же степени относящихся и к группе Юпитера (им соответствуют максимумы на фиг. 20.4, обозначенные вертикальными стрелками). Короче говоря, продолжения ряда планет земной группы не существует с квантовыми числами выше 10 по той простой причине, что вещества с меньшей плотностью попадают в группу Юпитера. За Плутоном могли бы находиться планеты с квантовыми числами 7 и 8, но непонятно, из чего они могут состоять. Если в космосе существует твердый водород и, соответственно, твердый высокопористый водород, то следует поискать эти планеты. Представляется более вероятным существование за Плутоном малых планет Солнечной системы с обратным движением, на что косвенно указывает "аномальный" (см. ниже) эксцентриситет орбиты Плутона. Все эти рассуждения справедливы для "правильных" планет и спутников, не захваченных Солнечной системой, как единое целое, а растущих естественным образом или захваченных достаточно давно и успевших стать “правильными”.
Еще одну особенность следует отметить в связи с "облучением" Солнечной системы двумя разными типами макротел. Подставив в (20.2) r0, найденное для планет земной и юпитерной групп, найдем:
![]() =0,908×1019 см2/сек для
земной группы и
=0,908×1019 см2/сек для
земной группы и
![]() =4,77×1019
см2/сек для юпитерной группы
(20.10),
=4,77×1019
см2/сек для юпитерной группы
(20.10),
|
|
|
|
|
|
т.е. момент количества движения макротел, образующих земную группу планет, как и предполагалось, почти в 5 раз меньше момента макротел, образующих планеты группы Юпитера. Именно поэтому первая группа планет вращается медленно вокруг собственной оси, а вторая быстро, т.е. космическое вещество не только подпитывает массой Солнце и планеты, но и поддерживает их вращение вокруг осей. Причем, чем больше планета, тем быстрей она вращается, поскольку быстрее растет. “Есть некая закономерность во вращении планет: чем больше масса планеты, тем быстрее она вращается”. А.В. Бялко, Наша планета - Земля, “Наука”, М., 1989, стр. 50. Воочию это можно видеть по преимущественному выпадению метеоритов на Землю в восточном направлении. “Ведь вся (практически вся) энергия метеорита уходит в конечном счете именно на нагревание горных пород, пройдя перед этим через другие, механические формы. Оговорка “практически” связана с изменением в результате столкновения с метеоритом скорости движения всей Земли и скорости ее вращения”. А.В. Бялко, Наша планета - Земля, “Наука”, М., 1989, стр. 81.
“Наиболее часто выпадают на Землю метеориты каменные, так называемые хондриты. Их силикатная структура содержит хондры - зерна размером до нескольких миллиметров”. Там же, стр. 80.
“Если предположить, что центральное твердое ядро (Земли - В.К.) состоит из железа, а жидкость - из окиси железа FeO и сернистого железа FeS, то химический состав всей нашей планеты целиком окажется близким к составу углистых хондритов”. Там же, стр. 93.
Захваченное вещество не дает орбитам планет стать точно в плоскость экватора Солнца, что видно из фигуры 20.1, а осям вращения планет препятствует расположиться точно перпендикулярно орбите. Угол между осью вращения планеты и плоскостью орбиты является, по сути, следствием угла между собственным моментом количества движения и вектором скорости макротела по витку винтовой линии. Многочисленные факты, показывающие, что вращение небесных тел производится внешним воздействием, компенсирующим диссипативные процессы, за недостатком места рассматривать не будем - они известны. Мы должны наблюдать также квантованность больших полуосей орбит астероидов и комет, являющуюся следствием гравидинамического самовоздействия свободных тел.
Для иллюстрации этого утверждения, на фигуре 20.5 представлена
зависимость ![]() (а.е.)1/2 от квантового
числа n для семейств комет Сатурна и Нептуна. r0
рассчитывалось по формуле (20.9), т.е. соответствует будущим круговым орбитам
комет. Кометы с №16 по №21, по-видимому, перегружены метеоритным веществом,
т.к. для них угол наклона прямой значительно меньше. Таким образом, всю глубину
общности макро- и микрокосмоса нам еще предстоит осознать в полной мере
(посмотрите квантовые состояния элементарных частиц в соответствующей главе).
(а.е.)1/2 от квантового
числа n для семейств комет Сатурна и Нептуна. r0
рассчитывалось по формуле (20.9), т.е. соответствует будущим круговым орбитам
комет. Кометы с №16 по №21, по-видимому, перегружены метеоритным веществом,
т.к. для них угол наклона прямой значительно меньше. Таким образом, всю глубину
общности макро- и микрокосмоса нам еще предстоит осознать в полной мере
(посмотрите квантовые состояния элементарных частиц в соответствующей главе).
Подставив выражение (20.10) и (20.2) в (20.5), найдем радиусы орбит планет Солнечной системы земной группы rз и группы Юпитера rю:
![]() (см)
(20.11),
(см)
(20.11),
![]() (см)
(20.12).
(см)
(20.12).
В таблице 20.1 указаны действительные (большая полуось орбиты) и вычисленные по (20.11) и (20.12) в предположении круговой орбиты радиусы орбит планет. В скобках указано квантовое состояние планет.
Таблица 20.1.
|
Планета |
радиус орб. 1013 см |
вычисл. 1013 см |
|
Меркурий(3) |
0,5791 |
0,559 |
|
Венера(4) |
1,0821 |
0,993 |
|
Земля(5) |
1,496 |
1,552 |
|
Марс(6) |
2,279 |
2,235 |
|
Юпитер(2) |
7,783 |
6,86 |
|
Сатурн(3) |
14,28 |
15,4 |
|
Уран(4) |
28,72 |
27,4 |
|
Нептун(5) |
44,98 |
42,8 |
|
Плутон(6) |
59,1 |
61,7 |
Было бы очень странно, если бы в Солнечной системе встречались тела только в разных квантовых состояниях. Это бы означало, что некий менеджер ведет их учет и поставляет в соответствии с утвержденным списком. Фактически это означает полную дискредитацию идеи квантованности макротел. Поэтому мы должны обнаруживать макротела в одном и том же квантовом состоянии. Земля и Луна могут рассматриваться как двойная планета в одном квантовом состоянии. “Исключительная массивность Луны позволяет называть систему Земля-Луна двойной планетой и считать, что условия образования этой системы несколько отличались от условий формирования других планет. Однако после крушения гипотезы английского физика Д. Дарвина об отделении Луны от Земли никакого иного объяснения столь значительным размерам Луны предложено не было”. “Физика космоса”, “Советская энциклопедия”, М., 1976, стр.66. Новая физика считает, что Луна захвачена Солнечной системой почти целиком и речь надо вести не об ее отделении от Земли, а падении на Землю. Подробнее о захвате Луны в конце главы.
Подобное положение в одном квантовом состоянии неустойчиво и должно приводить к слиянию макротел, но, учитывая их постоянное поступление в Солнечную систему, подобный феномен докажет одновременно и квантованность и непрерывный рост массы Солнечной системы. Для выяснения этого вопроса обратимся к спутникам планет. Проделав аналогичную процедуру для них, мы увидим, что качественная картина остается прежней, вплоть до копирования планетами юпитерной группы Солнечной системы в миниатюре (эти планеты, как увидим ниже, сами являются потенциальными звездами). “Спутник регулярный - спутники, образующие миниатюрные системы, подобные Солнечной, около трех самых крупных планет-гигантов. Это четыре галилеевых спутника Юпитера (открыты Г. Галилеем в 1610 г.), восемь классических спутников Сатурна и пять спутников Урана. Орбиты спутников регулярных, как правило, почти круговые и лежат вблизи экваторов планет. Предполагается, что системы спутников регулярных образовались под действием тех же процессов, которые привели к образованию самой Солнечной системы”. Е.Н. Слюта и др., Сравнительная планетология, “Наука”, М., 1995, стр.65-66.
Правда, в еще большей степени "квантованность" размазывается, т.к. она и для Солнечной системы не строгая, что видно по некоторому несовпадению рассчитанных и действительных радиусов орбит планет из-за существенных диссипативных процессов и возмущений. Для расчетов необходимы, как минимум, два спутника (далее будет показан путь расчета спутниковой системы, для которого необходимо знать только массу центрального тела).
Многочисленные наблюдаемые явления на Солнце подтверждают предположение о том, что наше светило не только теряет массу за счет излучения и “солнечного ветра”, но и приобретает ее (жаль, что не знаем сколько) за счет космического материала. “Наблюдается и явление, приводящее к росту массы Солнца. Это падение на Солнце комет. Было сфотографировано несколько комет, со скоростью 618 км/сек (вторая космическая скорость Солнца) устремлявшихся к солнечному диску. Это были небольшие кометы, они обнаружили себя свечением всего за несколько часов до своего исчезновения, до испарения в атмосфере Солнца. Оценить массу этих комет трудно. Трудно даже сказать, насколько часто происходят эти события - пока их зафиксировано слишком мало”. А.В. Бялко, Наша планета - Земля, “Наука”, М., 1989, стр. 114.
Очевидно, что метеоритная пыль должна давать яркие спектральные линии железа и никеля в короне. “Примерно в то же время была раскрыта загадка таинственного элемента “корония”, которому приписывались яркие линии короны. Оказалось, что они вызваны свечением железа и никеля, только находящихся в совершенно необычном состоянии, когда вследствие исключительно высокой температуры (примерно 1-2 млн. градусов) и разреженности атомы этих химических элементов теряют от девяти до четырнадцати электронов”. Ю.И. Витинский, Солнечная активность, “Наука”, М., 1983, стр.15.
“Падение” облаков космического водорода на Солнце вызывает не только вспышки, но и подтверждает еретическую мысль о том, что термоядерные реакции греют Солнце не только изнутри, но и снаружи. “По-видимому, где-то на границе фотосферы и хромосферы в результате сложного взаимодействия излучения, конвекции, а также магнитных и электрических полей происходит нечто необычное, непонятное. Потому что температура солнечного газа, которая до этого - от центра Солнца до фотосферы - убывала (как и положено при удалении от источника энергии), неожиданно начинает возрастать”. А.В. Бялко, Наша планета - Земля, “Наука”, М., 1989, стр. 129.
“Вспышка - очень сложное явление. Она проявляется прежде всего в кратковременном усилении электромагнитного излучения в широком диапазоне длин волн, от жестких рентгеновских лучей с длиной волны меньше 1А0, а в редких случаях от гамма лучей с длиной волны около 0,02 А0, до километровых радиоволн, и в выбросе ускоренных солнечных частиц. Кроме того, вспышки приводят к активизации процессов в других областях солнечной атмосферы, порой удаленных от них на десятки тысяч километров. А в некоторых наиболее мощных вспышках даже порождаются космические лучи, протоны которых обладают смертоносной энергией. Общая же энергия вспышки составляет 1029-1032 эрг, что сравнимо с энергией взрыва тысяч водородных бомб”. Ю.И. Витинский, Солнечная активность, “Наука”, М., 1983, стр. 36.
“Сама солнечная вспышка обычно начинается быстрым возрастанием температуры короны примерно до 40 млн. градусов, приводящим к появлению всплесков мягкого рентгеновского излучения”. Там же, стр. 37.
“Интересно, что в последние годы от нескольких протонных вспышек было зарегистрировано гамма-излучение, которое служит признаком наличия ядерных реакций в солнечной атмосфере. Оно появилось во время их импульсной стадии”. Там же, стр. 41.
Потоки вещества от Солнца мы фиксируем легко, но, к сожалению, очень трудно обнаружить обратный поток, даже падение комет на наше светило обнаруживается с большим трудом.
Будущие исследования покажут, какой из этих механизмов превалирует. “Результаты экспериментов оказались неожиданными. Нейтрино не были зарегистрированы: поток нейтрино оказался, по крайней мере, в пять раз меньше, чем было предсказано теорией. Эти эксперименты показали, что наши представления о процессах, протекающих в глубоких недрах звезд, не точны. По-видимому, недра Солнца холоднее, чем ранее предполагалось. Это означает, что из двух возможных термоядерных реакций - протон-протонной и углеродно-азотной – последняя, скорее всего не реализуется во внутренних областях Солнца”. Физика космоса, “Советская энциклопедия”, М., 1976, стр.382. Вполне возможно, также, что представления официальной физики об исключительной проникающей способности нейтрино не верны.
Комментарии автора к главе 20:
1. Взаимная метеоритная бомбардировка.
Этот вопрос удобно рассмотреть на примере системы Земля-Луна. Вращение Луны синхронное, т.е. она всегда повернута к Земле одной стороной. Противоположная сторона в значительной степени перехватывает метеориты, предназначенные Земле, поэтому обратная сторона Луны испещрена метеоритными кратерами и почти не имеет «морей». Земля экранирует видимую сторону Луны от метеоритной бомбардировки, поэтому она большей частью заполнена «морями» с незначительным числом кратеров. История Земли помнит падение на ее поверхность гигантских астероидов (например, Мексиканский залив). При этом часть обломков этих астероидов и земных пород выпадали в виде метеоритов на видимую сторону Луны. В свою очередь, обломки, образующиеся при ударе о лунную поверхность, возвращались в виде метеоритов к Земле.
|
|
|
|
|
|
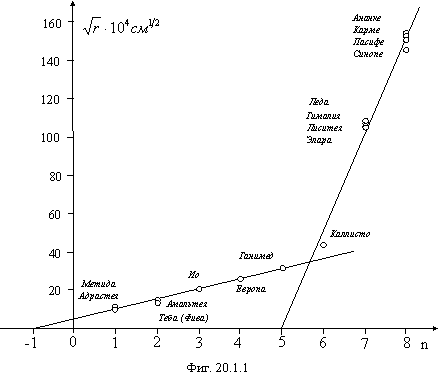
На фигуре 20.1.1 представлена
зависимость ![]() от целых чисел для спутников Юпитера. У Юпитера
качественная картина такая же, как и у всей Солнечной системы. Четко
разделяются спутники "земной" группы (первые семь) и
"юпитерной" группы. Юпитер находится в стадии интенсивного роста
массы (и вот-вот превратится в звезду, см. об этом ниже) о чем можно судить по
тому, что как спутники “земной” так и “юпитерной” групп находятся по несколько
штук в одном квантовом состоянии. Можно даже предполагать, что у Юпитера есть
свой пояс астероидов между спутниками "земной" и "юпитерной"
групп. Косвенно о расположении этого пояса астероидов между орбитами Ганимеда
(“земная” группа) и Каллисто (“юпитерная” группа) можно судить о насыщенности
поверхности этих спутников ударными кратерами. “Наиболее насыщена кратерами
поверхность Каллисто, самого далекого от Юпитера из галилеевых спутников, и в
меньшей степени поверхность Ганимеда. Свежие кратеры Каллисто и Ганимеда, за
исключением крупных многокольцевых образований, похожи на кратеры других
планетных тел. Смена типа строения кратеров от простых к сложным происходит при
диаметрах менее 10-20 км. На Европе обнаружены единичные кратеры. На Ио ударные
кратеры не найдены, очевидно, в силу того, что поверхность этого спутника
непрерывно обновляется активной современной вулканической деятельностью”. Е.Н.
Слюта и др. “Сравнительная планетология”, “Наука”, М., 1995, стр.35-36.
от целых чисел для спутников Юпитера. У Юпитера
качественная картина такая же, как и у всей Солнечной системы. Четко
разделяются спутники "земной" группы (первые семь) и
"юпитерной" группы. Юпитер находится в стадии интенсивного роста
массы (и вот-вот превратится в звезду, см. об этом ниже) о чем можно судить по
тому, что как спутники “земной” так и “юпитерной” групп находятся по несколько
штук в одном квантовом состоянии. Можно даже предполагать, что у Юпитера есть
свой пояс астероидов между спутниками "земной" и "юпитерной"
групп. Косвенно о расположении этого пояса астероидов между орбитами Ганимеда
(“земная” группа) и Каллисто (“юпитерная” группа) можно судить о насыщенности
поверхности этих спутников ударными кратерами. “Наиболее насыщена кратерами
поверхность Каллисто, самого далекого от Юпитера из галилеевых спутников, и в
меньшей степени поверхность Ганимеда. Свежие кратеры Каллисто и Ганимеда, за
исключением крупных многокольцевых образований, похожи на кратеры других
планетных тел. Смена типа строения кратеров от простых к сложным происходит при
диаметрах менее 10-20 км. На Европе обнаружены единичные кратеры. На Ио ударные
кратеры не найдены, очевидно, в силу того, что поверхность этого спутника
непрерывно обновляется активной современной вулканической деятельностью”. Е.Н.
Слюта и др. “Сравнительная планетология”, “Наука”, М., 1995, стр.35-36.
"Земная" группа Юпитера: r=r0×n2=0,273×1010×n2 (см),
![]() = 1,86 · 1016 см2/сек.
= 1,86 · 1016 см2/сек.
|
Спутник |
радиус орб. 1010 см |
выч. 1010 см |
|
Метида (2) Адрастея (2) |
1,28 1,29 |
1,09 |
|
Амальтея (3) Теба (Фива) (3) |
1,81 2,22 |
2,46 |
|
Ио(4) |
4,22 |
4,37 |
|
Европа(5) |
6,71 |
6,82 |
|
Ганимед(6) |
10,70 |
9,83 |
“Юпитерная” группа Юпитера: r=r0×n2=25×1010×n2 (см).
![]() =17,8 ×1016
см2/сек.
=17,8 ×1016
см2/сек.
|
Спутник |
радиус орб. 1010 см |
выч. 1010 см |
|
Каллисто (1) |
18,83 |
25,0 |
|
Леда (2) Гималия (2) Лиситея (2) Элара (2) |
110,9 114,8 117,2 117,4 |
100,0 |
|
Ананке (3) Карме (3) Пасифе (3) Синопе (3) |
212 226 235 237 |
225 |
Если в Солнечной системе в целом возникает подозрение, что такие планеты как Меркурий (из-за большого эксцентриситета), Венера (из-за обратного вращения вокруг оси) “Радиолокационные наблюдения позволяют сделать вывод, что Венера, в отличие от других планет, вращается в сторону, противоположную направлению ее движения вокруг Солнца, с периодом, близким к 243 суткам”. В.Г. Демин “Судьба Солнечной системы”, “Наука”, М., 1975, стр.16., Уран (из-за большого наклона оси вращения), Плутон (из-за большого эксцентриситета и большого угла наклона плоскости орбиты к плоскости эклиптики) захвачены Солнечной системой целиком или в большей их части, то строение спутниковой системы Юпитера (как и спутниковых систем других планет) укрепляет в этом подозрении. По мере удаления спутников от Юпитера и ослабления гравидинамического поля, эксцентриситеты и углы наклона плоскостей орбит увеличиваются, обратное движение наружных спутников и нахождение большинства спутников в одних и тех же квантовых состояниях с очевидностью доказывают, что захват преобладает над постепенным ростом членов Солнечной системы. “Наиболее загадочная и не объяснимая космогонией особенность спутников Юпитера связана с четырьмя внешними спутниками, обращающимися вокруг Юпитера в направлении, противоположном направлению движения большинства других спутников планет”. Там же, стр.26. “Спутник нерегулярный (обратный) - спутник с вытянутой, сильно наклоненной (часто обратной) орбитой, которая указывает на захват этих тел. Орбиты спутников нерегулярных расположены во внешних областях гравитационного поля планет. У Юпитера спутники нерегулярные образуют две группы по четыре члена в каждой. Первая или внутренняя группа находится на расстоянии 160R (радиусов Юпитера) и характеризуется эксцентриситетом e~0,15 и наклонением орбит i~280. Внешняя группа находится на расстоянии 360R, e~0,25 и i~1500. Спутник Сатурна Феба и спутник Нептуна Нереида также являются спутниками нерегулярными”. Е.Н. Слюта и др. “Сравнительная планетология”, “Наука”, М., 1995, стр.65.
Как и следовало ожидать, из-за большого удаления от Солнца, в спутниковой системе Юпитера мы обнаруживаем спутники “земной” и “юпитерной” группы с низкими квантовыми числами, начиная с n=1. Спутник 1 “земной” группы не может существовать в виде цельного космического тела из-за сильного приливного воздействия Юпитера, поэтому мы наблюдаем кольцо Юпитера. “Кольцо Юпитера - расположено в экваториальной плоскости на расстоянии 55 000 км от видимой границы облаков (около 3/4 радиуса планеты). Ширина кольца 6 000 км при толщине около 1 км. Образовано частицами с низкой отражательной способностью (менее 5%) и размерами от нескольких микрометров до нескольких метров”. Е.Н. Слюта и др. “Сравнительная планетология”, “Наука”, М., 1995, стр.29.
На фигуре 20.1.2 представлена зависимость ![]() от целых чисел для
спутниковой системы Сатурна.
от целых чисел для
спутниковой системы Сатурна.
"Земная" группа Сатурна: r=r0×n2=3,65×108×n2 (см),
![]() =3,72×1015
см2/сек.
=3,72×1015
см2/сек.
|
|
|
|
|
|
Интересно отметить, что квантовые числа спутников имеют большие значения, по-видимому, из-за знаменитого кольца Сатурна, реализовавшего все меньшие квантовые числа. “Кольца планет - совокупность отдельных небольших тел или частиц, окружающих планеты-гиганты в виде широких (в плоскости орбиты) и тонких кольцевых образований. Предполагается, что кольца, расположенные обычно в пределе Роша (ближе спутник разрушается от действия приливных сил и образование единого тела невозможно - В.К.), представляют собой материал не сформировавшихся спутников.
Кольца Сатурна - выделяется семь основных колец, которые в направлении от планеты носят следующие названия: D, C, B, A, F, G, E. Предполагается, что кольца Сатурна образованы преимущественно частицами водного льда размерами от нескольких микрометров до десятков сантиметров и нескольких метров. Кольцо D находится в 7000 км от границы облачного слоя планеты. Кольца A, B и С характеризуются сложной внутренней структурой и состоят из тысяч отдельных колечек шириной от нескольких километров до нескольких десятков километров. В целом ширина каждого из колец А и С составляет около 17 000 км, а В - около 28000 км. Толщина их не превышает 1-2 км. Кольцо F характеризуется рядом отличительных особенностей, оно состоит из отдельных “прядей”, отклоняющихся от эллиптической траектории и иногда переплетающихся между собой. Ширина его около 200 км. Кольцо Е также однородное без каких-либо деталей и занимает зону от трех до восьми радиусов Сатурна. Предполагается, что происхождение частиц этого кольца может быть обусловлено вулканическими извержениями в прошлом на спутнике Энцеладе, орбита которого проходит в центре этой зоны. Промежутки в кольцах, связанные с наличием резонансов в общей динамической системе планета-спутники, носят название делений. Иногда в кольцах наблюдаются так называемые “спицы””. Е.Н. Слюта и др. “Сравнительная планетология”, “Наука”, М., 1995, стр.28-29.
““Спицы” в кольцах Сатурна - радиальные образования в кольцах планеты, которые выглядят темными в отраженном и светлыми в проходящем свете на окружающем их фоне. Длина “спиц” достигает 10 000 км, ширина 1000 км. Время их жизни не превышает нескольких часов. Предполагается, что они образованы облаками частиц размерами меньше 1 мм, “парящими” над основными кольцами на высоте всего в десятки метров”. Там же, стр.65.
|
Спутник |
радиус орб. 1010 см |
выч. 1010 см |
|
Атлант (5) Прометей (5) Пандора (5) |
1,38 1,39 1,42 |
0,91 |
|
Эпиметей (6) Янус (6) |
1,51 1,51 |
1,31 |
|
Мимас (7) |
1,85 |
1,79 |
|
Энцелад (8) |
2,38 |
2,34 |
|
Тефия (9) Телесто (9) Калипсо (9) |
2,95 2,95 2,95 |
2,96 |
|
Диона (10) Елена (10) |
3,77 3,77 |
3,65 |
"Юпитерная" группа Сатурна: r=r0×n2=1,39×1010 (см).
![]() =2,296×1016
см2/cек.
=2,296×1016
см2/cек.
|
Спутник |
радиус орб. 1010 см |
выч. 1010 см |
|
Рея(2) |
5,27 |
5,56 |
|
Титан(3) |
12,22 |
12,5 |
|
Гиперион(4) |
14,81 |
22,2 ? |
|
Япет(5) |
35,61 |
34,7 |
|
Феба (10) |
129,52 |
139 |
Гиперион "выпадает" из установленной закономерности из-за отсутствия “квантованности”. Этот случай очень интересен с точки зрения новой физики и указывает на то, что в результате возмущений “волна де Бройля” макротел в космическом пространстве может значительно искажаться. Первопричиной таких искажений является изменение вращения тела вокруг своей оси. Подтверждением тому может служить хаотичное вращение Гипериона вокруг оси - уникальный случай для спутников планет. Гиперион и Феба имеют явные признаки захвата их целиком, а не постепенного роста (значительный эксцентриситет орбит, обратное движение Фебы).
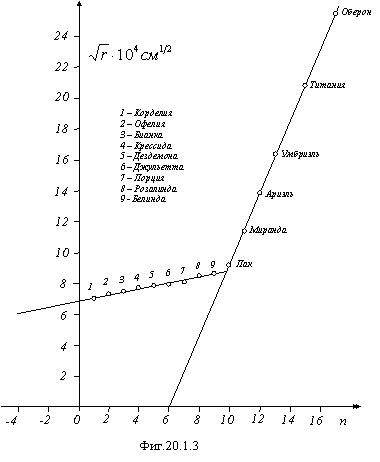
На фигуре 20.1.3 представлена зависимость ![]() от целых чисел для
спутниковой системы Урана.
от целых чисел для
спутниковой системы Урана.
|
|
|
|
|
|
У Урана "земная" группа: r=r0×n2=0,04×108×n2 (см),
![]() =1,522×1014 см2/сек.
=1,522×1014 см2/сек.
Меньшие квантовые числа спутников "земной" и "юпитерной" группы, по-видимому, как и в случае Сатурна, реализованы кольцами Урана. “Кольца Урана - известно 11 узких основных колец сложенных (кроме вновь открытых колец - 1986U2R и 1986U1R) частицами размерами от 10 см до нескольких метров, и около 100 почти прозрачных поясов, сложенных частицами размерами около 0,02 мм, включая и вновь открытые узкие кольца. Все кольца обладают очень низкой отражательной способностью (альбедо менее 5%). ... Не все кольца имеют круговую форму и не все лежат в плоскости экватора. Кольца отличаются также шириной, которая для разных колец меняется в пределах от 2 до 100 км”. Е.Н. Слюта и др. “Сравнительная планетология”, “Наука”, М., 1995, стр.29.
Уран со своими спутниками является уникальным образованием в Солнечной системе из-за особенностей его вращения вокруг оси. “Он движется вокруг Солнца, лежа “на боку”. Дело в том, что ось его вращения образует с нормалью к плоскости орбиты угол 980 , т.е. лежит почти в плоскости его орбиты, и к тому же направлена в сторону, противоположную обычному направлению осей вращения всех других планет Солнечной системы. ... Необычно не только вращение самого Урана, но и обращение вокруг него всех его пяти известных спутников (сейчас их известно больше - В.К.), которые движутся по сравнению со спутниками других больших планет в обратном направлении. Причина отмеченных “странностей” движений в системе Урана пока не выяснена. Более того, эти особенности не укладываются ни в одну из предлагавшихся гипотез происхождения Солнечной системы”. В.Г. Демин “Судьба Солнечной системы”, “Наука”, М., 1975, стр. 22-23.
Новая физика дает простое объяснение феномену Урана.
Он вместе со спутниками образовался в межзвездном пространстве (см. далее главу о космологии) и был целиком захвачен Солнечной системой с обратным движением. За счет гравидинамического воздействия, орбита Урана была постепенно повернута так, чтобы движение вокруг Солнца стало “нормальным” и в настоящее время происходит переворачивание собственного гравидинамического момента Урана параллельно общему гравидинамическому моменту Солнечной системы. В конечном итоге, феномен Урана исчезнет. На это указывает и “выпадение” массы Урана из ряда масс планет-гигантов, поскольку за время эволюции своей орбиты он терял массу, но не имел возможности естественного роста за счет космического материала, поэтому у него нет спутников в одном и том же квантовом состоянии.
|
Спутник |
радиус орб. 1010 см |
выч. 1010 см |
|
Корделия (35) |
0,497 |
0,49 |
|
Офелия (36) |
0,538 |
0,52 |
|
Бианка (37) |
0,592 |
0,55 |
|
Крессида (38) |
0,618 |
0,58 |
|
Дездемона (39) |
0,627 |
0,61 |
|
Джульетта (40) |
0,644 |
0,64 |
|
Порция (41) |
0,661 |
0,67 |
|
Розалинда (42) |
0,699 |
0,71 |
|
Белинда (43) |
0,752 |
0,74 |
Исключительно большие квантовые числа спутников Урана “земной” группы соответствуют квантовым числам комет семейств Сатурна и Нептуна, перегруженных метеоритным материалом (см. фигуру 20.5, №16 - №21). Учитывая, что спутниковая система Урана сохранилась почти в “первозданном” состоянии, подобный результат наводит на мысль, что на окраинах Солнечной системы мы должны обнаруживать большое количество строительного материала (как увидим ниже, это замечание справедливо и к окраинам галактик, где мы пока ничего не видим). “Периферия Солнечной системы пока еще исследована мало. Не исключено, что, кроме комет и газопылевых облаков, на далеких окраинах Солнечной системы существуют еще не
открытые планеты”. “Физика космоса”, “Советская энциклопедия”, М., 1976, стр.80.
“Существование Солнечной системы обусловлено действием солнечной гравитации, поэтому естественно определить границы Солнечной системы как границы области, где преобладает притяжение Солнца. Радиус этой области, вычисленный без учета световой репульсии, оценивается в 2×105 а.е., а полная масса заключенной в ней диффузной материи оказывается равной массе Солнца (2×1033 г)”. Там же, стр.79.
О причинах больших квантовых чисел смотрим также ниже.
"Юпитерная" группа Урана:
r=r0×n2= 4,814×108×n2
(см), ![]() =1,670×1015
см2/сек.
=1,670×1015
см2/сек.
В “юпитерной” группе Урана трудно ожидать спутники в одном и том же квантовом состоянии (нет условий для их захвата), но могут отсутствовать некоторые квантовые состояния, особенно на периферии, где гравитационное поле ослаблено, что и наблюдается в действительности.
|
Спутник |
радиус орб. 1010 см |
выч. 1010 см |
|
Пак (4) |
0,860 |
0,77 |
|
Миранда (5) |
1,298 |
1,20 |
|
Ариэль (6) |
1,912 |
1,73 |
|
Умбриэль (7) |
2,660 |
2,36 |
|
Титания(9) |
4,358 |
3,90 |
|
Оберон(11) |
5,826 |
5,82 |
На фигуре 20.1.4 представлена зависимость ![]() от целых чисел для
спутниковой системы Нептуна.
от целых чисел для
спутниковой системы Нептуна.
Несмотря на то, что самый массивный спутник Нептуна - Тритон имеет обратное движение, что указывает на его захват целиком или в большей своей части, он находится в первом квантовом состоянии “юпитерной” группы. “Интересный космогонический результат был получен Т. Маккордом, изучавшим движение спутников Нептуна. По его мнению, благодаря приливному трению Нептун приобрел спутник Тритон, который в прошлом двигался по параболической орбите”. В.Г. Демин, Судьба Солнечной системы, “Наука”, М., 1975, стр.165.
Спутник Нереида совсем недавно захвачен
(по астрономическим масштабам времени) и имеет очень большой эксцентриситет
орбиты (е=0,75), поэтому приходится рассчитать его будущее стационарное
состояние по формуле: ![]() , где а - большая полуось орбиты,
равная 55,134×1010 см. Все данные для планет, спутников,
комет и астероидов взяты из книги: Е.Н. Слюта и др. “Сравнительная
планетология”, “Наука”, М., 1995, стр.78-105.
, где а - большая полуось орбиты,
равная 55,134×1010 см. Все данные для планет, спутников,
комет и астероидов взяты из книги: Е.Н. Слюта и др. “Сравнительная
планетология”, “Наука”, М., 1995, стр.78-105.
Эта формула легко получается из (20.9), если учесть, что rn=a(1-e). Её также можно получить, приравнивая разницу потенциальной энергии гравитации в точках перигелия и афелия разнице “кинетической” (в терминах официальной науки) энергии в этих же точках. По представлениям новой физики на эллиптической орбите происходит колебательный процесс перехода потенциальной энергии притяжения в потенциальную энергию отталкивания и наоборот, подобно колебанию грузика, подвешенного на пружине. В отсутствие диссипативных процессов эллиптическая орбита была бы устойчивой, но поскольку в макромире рассеяние энергии неизбежно, то она постепенно преобразуется в круговую.
|
|
|
|
|
|
Сегодняшнее положение большой полуоси Нереиды показано на фигуре 20.1.4 темной точкой. Остальные спутники в Солнечной системе не имеют столь больших эксцентриситетов, поэтому в предыдущих расчетах предполагались круговые орбиты.
“Земная” группа Нептуна: r=r0×n2=3,305×108×n2 (см).
![]() =1,500×1015
см2/сек.
=1,500×1015
см2/сек.
|
Спутник |
радиус орб. 1010 см |
выч. 1010 см |
|
1989N6 (4) 1989N5 (4) 1989N3 (4) |
0,482 0,500 0,525 |
0,53
|
|
1989N4 (5) 1989N2 (5) |
0,620 0,736 |
0,83 |
|
Протей (6) |
1,176 |
1,19 |
Меньшие квантовые числа спутников “земной” группы Нептуна, по-видимому, реализованы кольцами Нептуна. “По данным, полученным с космического аппарата Вояджер-2, известны три кольца - внешнее, среднее и внутреннее на расстояниях от планеты: 63 000, 53 000 и 42 000 км соответственно. Ширина каждого кольца не превышает 10 км. Наклонение колец к экватору планеты составляет ~00. Внешнее кольцо характеризуется сложной внутренней структурой: на общем фоне кольца наблюдаются отдельные переплетающиеся “пряди” шириной 2-5 км и располагающиеся на расстоянии друг от друга (вдоль по кольцу) в сотни километров”. Там же, стр.28.
“Юпитерная” группа Нептуна: r=r0×n2=5,443×1010×n2 (см).
![]() =1,924×1016
см2/сек.
=1,924×1016
см2/сек.
|
Спутник |
радиус орб. 1010 см |
выч. 1010 см |
|
Тритон (1) |
3,548 |
5,44 |
|
Нереида (2) |
24,121 (стац.) |
21,8 |
Чтобы убедиться в том, что значения ![]() , вычисленные из реального
устройства спутниковых систем, Солнца и планет не являются математической
абстракцией для подгонки теории под реальное положение вещей, построим зависимость
, вычисленные из реального
устройства спутниковых систем, Солнца и планет не являются математической
абстракцией для подгонки теории под реальное положение вещей, построим зависимость
![]() от
массы центрального тела для спутников "земной" и “юпитерной” группы,
что отражено на фигуре 20.1.5.
от
массы центрального тела для спутников "земной" и “юпитерной” группы,
что отражено на фигуре 20.1.5.
|
|
|
|
|
|
Спутниковая система Урана (5, фиг. 20.1.5) по вышеупомянутым причинам (длительное существование в изоляции от естественного роста) выпадает из этой зависимости. Неплохо бы этот график описать аналитической зависимостью - это очень важно в связи с обсуждаемой ниже возможностью косвенного определения наличия внеземных цивилизаций, но за неимением идеи расчетов, ограничимся эмпирической зависимостью a (см2/сек) спутниковой системы от массы М (г) центрального тела.
Эту зависимость можно описать формулами:
![]() (20.1.1),
(20.1.1),
![]() (20.1.2),
(20.1.2),
соответственно, для спутников "земной" и "юпитерной" группы.
Подставив (20.2) в (20.5), получим:
![]() (20.1.3),
(20.1.3),
подставив (20.1.1) и (20.1.2) в (20.1.3), найдем:
![]() (20.1.4),
(20.1.4),
![]() (20.1.5).
(20.1.5).
Например, для звезды с массой в 5 раз больше Солнца (таких звезд большинство) в соответствии с этими формулами планеты "земной" группы будут в 3,5 раза дальше от звезды, чем в Солнечной системе, а планеты "юпитерной" группы в 2,5 раза дальше. Чем больше масса центрального тела, тем дальше расположены от него спутники. Это мы можем наблюдать и непосредственно.
В этой связи и с учетом интенсивного роста Солнечной системы в прошлом, в основном, за счет самого Солнца, планеты постепенно удаляются от светила. Поэтому Марс демонстрирует будущее Земли, а Венера - далекое прошлое. “Из обработки полученных автоматическими межпланетными станциями материалов вытекает, что наиболее вероятные значения температуры на поверхности Венеры лежат в диапазоне 400 – 500 0С, а давление - в интервале 60 -140 атмосфер. Из измерений, проведенных межпланетными станциями, следует, что в атмосфере Венеры преобладает углекислый газ (93 -97%). В ней обнаружен также кислород, азот и водяные пары”. В.Г. Демин, Судьба Солнечной системы, “Наука”, М., 1975, стр. 16.
Прекрасную статью по этому поводу написал Г.А. Скоробогатов в журнале “Химия и жизнь”, №12, 1983 г. “Где оно, “космическое чудо”?”, в которой показал, что жизнь на Марсе не могла достичь развитых форм из-за слишком короткого периода благоприятных условий на этой планете. По-видимому, через пару миллиардов лет Венера для человечества окажется более благоприятным “домом”, чем Земля (если человечество останется к тому времени).
Мы видим, что, действительно, космическое вещество сепарируется по значениям
![]() в
зависимости от массы тела, образующего спутниковую систему. Когда спутниковая
система уже образована, дальнейшее наращивание ее массы не вызывает вопросов.
Вопрос состоит в том, откуда спутник "знает" где ему зарождаться?
Ответ на этот вопрос может быть в изначальной квантованности значений
в
зависимости от массы тела, образующего спутниковую систему. Когда спутниковая
система уже образована, дальнейшее наращивание ее массы не вызывает вопросов.
Вопрос состоит в том, откуда спутник "знает" где ему зарождаться?
Ответ на этот вопрос может быть в изначальной квантованности значений ![]() свободных
макротел. Она может возникнуть только в том случае, если между собой слипаются
частицы с одинаковой длиной волны де Бройля, т.е. происходит
"интерференция" этих волн. Вероятность образования макротела из
частиц с разным значением a,
по-видимому, очень мала, т.к. они не могут находиться рядом достаточное время.
Квантованность макротел является, в конечном итоге, следствием квантованности
микрочастиц. Более подробно этот вопрос рассматривается при обсуждении движения
фотонов. Таким образом, образование самих макротел, являющихся строительным материалом
планет и спутников происходит тоже с помощью описанного выше механизма.
Поскольку в мире микрочастиц возникает тоже потребность в ответе на подобный
вопрос, он дан в соответствующем разделе.
свободных
макротел. Она может возникнуть только в том случае, если между собой слипаются
частицы с одинаковой длиной волны де Бройля, т.е. происходит
"интерференция" этих волн. Вероятность образования макротела из
частиц с разным значением a,
по-видимому, очень мала, т.к. они не могут находиться рядом достаточное время.
Квантованность макротел является, в конечном итоге, следствием квантованности
микрочастиц. Более подробно этот вопрос рассматривается при обсуждении движения
фотонов. Таким образом, образование самих макротел, являющихся строительным материалом
планет и спутников происходит тоже с помощью описанного выше механизма.
Поскольку в мире микрочастиц возникает тоже потребность в ответе на подобный
вопрос, он дан в соответствующем разделе.
Вспомнив наши рассуждения об эллиптических орбитах в разделе описания атомов, мы можем сделать вывод о том, что эксцентриситеты орбит планет вызваны непрерывным поступлением вещества в эти планеты. Вместе с веществом они получают и избыточную механическую энергию. “Количество межпланетной пыли, выпадающей ежегодно на Землю, составляет ~106 т в год; количество выпадающего вещества с диаметром отдельных частичек больше 25 мкм составляет ~103 т в год; плотность пылевых частиц в окрестности Земли ~10-24 г/см3 ”. “Физика космоса”, “Советская энциклопедия”, М., 1976, стр.370.
“Значения эксцентриситета Земли колеблются около 0,028. Сейчас этот эксцентриситет меньше среднего и продолжает уменьшаться. Через 25 тысяч лет орбита Земли станет почти круговой”. А.В. Бялко “Наша планета - Земля”, “Наука”, М., 1989, стр.38.
Небольшие планеты, к которым относятся планеты земной группы будут иметь эксцентриситет орбит обратно пропорциональный их массам. Действительно, их эксцентриситеты удовлетворительно укладываются в зависимость:
![]() , где
K=6,5×1025 г.
(20.1.6).
, где
K=6,5×1025 г.
(20.1.6).
У планет юпитерной группы огромные массы, за исключением Плутона, поэтому их эксцентриситеты практически не чувствительны к массам этих планет и не реагируют на рост массы. У Плутона по зависимости (20.1.6) K=1,25×1027 г. Очень малое значение эксцентриситета орбиты Нептуна можно объяснить тем, что им захвачен сравнительно недавно в качестве спутника Тритон, как целое небесное тело, что подтверждает его аномальная масса и обратное движение. Поэтому избыточная механическая энергия Нептуна на определенное время почти пришла в соответствие с энергией притяжения к Солнцу.
Здесь необходимо обратить внимание на то, что диссипативные процессы в каждом небесном теле Солнечной системы достаточно ощутимы. Наличие эксцентриситетов орбит, наклонов орбит к плоскости Солнечного экватора, наклонения осей вращения к плоскости орбиты, вращение тел вокруг осей можно объяснить только одним - постоянной подпиткой всех членов Солнечной системы веществом и поддержание в связи с этим их "возбужденного" состояния.
Эта “подпитка” крайне неравномерна во времени и связана с прохождением Солнечной системы через пылевые облака: “Обнаружено несколько десятков ледниковых периодов в истории Земли. Повторяются они нерегулярно, промежутки между ними колеблются от 40 тысяч до нескольких сот тысяч лет. Между ледниковыми периодами климат возвращался более или менее к современному состоянию. Последний же ледниковый период отложил свои конечные морены всего 20 тысяч лет назад”. А.В. Бялко “Наша планета - Земля”, “Наука”, М., 1989, стр.211.
Для интенсивно поглощающих космический материал тел, таких как Солнце и планеты юпитерной группы, характерно экваториальное ускорение вращения, т.к. поступление внешнего вещества максимально в экваториальной плоскости: “Планеты-гиганты отличаются относительно высокой угловой скоростью осевого вращения и связанным с этим значительным сжатием. Интересной особенностью их вращения является так называемое экваториальное ускорение (с приближением к экватору возрастает не только линейная, но и угловая скорость вращения атмосферы”. “Физика космоса”, “Советская энциклопедия”, М., 1976, стр.65). С точки зрения ортодоксальной науки этот факт совершенно непонятен, т.к. из-за трения в атмосфере эффект экваториального ускорения не должен наблюдаться. С точки зрения новой физики, экваториальное ускорение доказывает “возбужденное” состояние космических тел за счет внешних факторов.
Если мы будем оставаться на позициях "рождения" Солнечной системы, как целого, при любом механизме этого рождения, то все перечисленные параметры возбужденного состояния давно должны были бы принять нулевое значение. Пожалуй, в этом главный козырь излагаемых взглядов на образование и строение Солнечной системы. В этой связи кажется удивительным, что не гравитационное, а несравненно более слабое, в данных условиях, гравидинамическое поле определяет облик Солнечной системы не только в общих чертах, но и в частностях. Мало того, оно является как бы мотором Солнечной системы, успешно конкурируя с гравитационным полем, влияние которого сводится к "торможению", т.е., в основном, к диссипативным процессам.
В центре галактик не обязательно иметь значительную притягивающую
массу. Каждая звезда может считаться практически свободной, а
центростремительную силу заменяет сила Лоренца для гравидинамического поля. По
этой причине, вероятно, в галактиках астрономы и не досчитываются массы,
необходимой для наблюдаемого движения звезд. В этом случае ![]() для каждой
звезды (для Солнца 9×1029 см2/сек)
будет определяться плотностью, скоростью вращения и скоростью движения в
галактике (намеренно речь не будем вести о галактической "орбите").
Эти же факторы определяют и положение звезды в галактике, следовательно, ее
строение. Подробнее смотрим в главе, посвященной космологии.
для каждой
звезды (для Солнца 9×1029 см2/сек)
будет определяться плотностью, скоростью вращения и скоростью движения в
галактике (намеренно речь не будем вести о галактической "орбите").
Эти же факторы определяют и положение звезды в галактике, следовательно, ее
строение. Подробнее смотрим в главе, посвященной космологии.
Необходимо более внимательно посмотреть и на магнитные поля в космосе, гравидинамическое поле проявляет себя внешне точно таким же образом, поэтому многое из того, что мы относим к магнитному полю вполне может оказаться проявлением гравидинамического поля, тем более, что для этого не нужно веществ с магнитными свойствами или движения электрических зарядов.
Возвращаясь снова к Солнечной системе, можно утверждать, что по мере роста массы планет и спутников за счет космического вещества в соответствии с его природным распределением по химсоставу и плотности. Радиус орбит планет не меняется только в том случае, если неизменна масса Солнца. Прирост его массы в современный период, по-видимому, равен потерям, на что указывает стабильность постоянной излучения. Любая звезда неизбежно образует вокруг себя спутниковую систему очень похожую на Солнечную систему не только с подобным распределением радиусов орбит и масс планет, но и с подобным распределением химсостава. Поскольку Солнце является заурядной звездой во Вселенной, шансы найти братьев по разуму очень велики.
В заключение этого раздела решим одну интересную задачу.
Предположим, что мы закрываем некоторую поверхность n слоями
статистически расположенных в каждом слое тел, не перекрывающих друг друга в
данном слое, с коэффициентом заполнения площади в каждом слое ![]() , где
, где ![]() <1, а
s -
площадь, перекрываемая телами в каждом слое. Требуется определить общий
коэффициент заполнения площади
<1, а
s -
площадь, перекрываемая телами в каждом слое. Требуется определить общий
коэффициент заполнения площади ![]() в зависимости от числа слоев n.
в зависимости от числа слоев n.
В свое время, в области математики, автор открыл множество новых исчислений, аналогичных дифференциальному и интегральному. Они настолько важны в прикладном плане, что даны в приложении к этой книге, благо, что основной принцип новых исчислений прост, и его можно изложить на нескольких страницах. По одному из этих исчислений ответ получить легко:
![]() (20.1.7).
(20.1.7).
Нас, в данном случае, будет интересовать применение формулы (20.1.7)
для астрономии. Предположим, что в данной области космического пространства
средняя плотность вещества составляет ![]() г/см3.
Если в некотором объеме V будет находиться шарообразное тело массой m,
то, очевидно, что:
г/см3.
Если в некотором объеме V будет находиться шарообразное тело массой m,
то, очевидно, что: ![]() ,
, ![]() , где: r- радиус
тела, а
, где: r- радиус
тела, а ![]() - его плотность.
- его плотность. ![]() , а толщина
одного слоя с расположенным в нем одним телом
, а толщина
одного слоя с расположенным в нем одним телом ![]() . Число слоев
. Число слоев ![]() , где X
- расстояние.
, где X
- расстояние. ![]() примем равным 0,99 , что означает
практически сплошное (на 99%) заполнение участка небосвода звездами или,
наоборот, его непрозрачность из-за поглощающего свет материала. Подставив все
значения в (20.1.7) и обозначив
примем равным 0,99 , что означает
практически сплошное (на 99%) заполнение участка небосвода звездами или,
наоборот, его непрозрачность из-за поглощающего свет материала. Подставив все
значения в (20.1.7) и обозначив 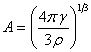 , после небольших преобразований, получим:
, после небольших преобразований, получим:  .
Логарифмируя обе части уравнения, найдем:
.
Логарифмируя обе части уравнения, найдем: ![]() . Учитывая, что абсолютная
величина
. Учитывая, что абсолютная
величина ![]() очень мала, заменим
очень мала, заменим ![]() его приближенным
значением из разложения в ряд Тейлора:
его приближенным
значением из разложения в ряд Тейлора: ![]() , тогда найдем
окончательно:
, тогда найдем
окончательно:
![]() (20.1.8).
(20.1.8).
Выражение (20.1.8) позволяет сделать некоторые оценочные расчеты
относительно материи в космосе, в том числе и не светящейся. Так, например, для
того, чтобы статистически расположенные в пространстве звезды практически
полностью заполнили участок небосвода (на 99%), радиус Вселенной должен
составить 3×1021 световых
лет, а для наблюдаемого радиуса 5×109 световых
лет коэффициент заполнения составит всего 3×10-12 при
![]() =2×10-28 г/см3. Если
считать, что на расстоянии 5×109 световых
лет статистически расположенные темные тела заполняют небосвод на 99%, то
радиус таких тел должен быть не менее 0,8 мм. Для более крупных тел Вселенная будет
прозрачна. Для нашей Галактики средняя плотность звездного вещества по (20.1.8)
составит 10-11 г/см3, примерно такая же придется и
на не светящиеся тела. Приведенные оценки не противоречат предположению о
наличии во Вселенной большого количества материи, не выдающей своего
присутствия каким-либо излучением или экранированием удаленных объектов. Этот
вывод важен для понимания эволюции вещества во Вселенной и этот вопрос мы
частично затронем в дальнейшем.
=2×10-28 г/см3. Если
считать, что на расстоянии 5×109 световых
лет статистически расположенные темные тела заполняют небосвод на 99%, то
радиус таких тел должен быть не менее 0,8 мм. Для более крупных тел Вселенная будет
прозрачна. Для нашей Галактики средняя плотность звездного вещества по (20.1.8)
составит 10-11 г/см3, примерно такая же придется и
на не светящиеся тела. Приведенные оценки не противоречат предположению о
наличии во Вселенной большого количества материи, не выдающей своего
присутствия каким-либо излучением или экранированием удаленных объектов. Этот
вывод важен для понимания эволюции вещества во Вселенной и этот вопрос мы
частично затронем в дальнейшем.
Наконец, коснемся вопроса истории и будущего Земли. По всей видимости, мы живем в эпоху небольшого поступления в Солнечную систему нового строительного материала (за исключением водорода). Об этом, в частности, можно судить по довольно ощутимому замедлению вращения Земли и по тому, что Луна повернута к нам одной стороной и не изменила своего облика за время наблюдений (тут надо иметь в виду, что основная часть метеоритов и пыли должна выпадать на невидимую сторону Луны). “На экваторе при замедлении вращения Земли g уменьшается, на полюсах растет, а постоянным остается на широте 350. Интересно, что современная точность измерения ускорения свободного падения оказывается достаточной для того, чтобы заметить эти изменения - порядка 10-7 м/с2 за год”. А.В. Бялко, Наша планета - Земля, “Наука”, М., 1989, стр. 62.
Принимая, что в настоящее время ежегодно на Землю выпадает 2×1012 г метеоритного вещества (теперь эту цифру надо бы уточнить), нетрудно подсчитать, что в среднем за историю Земли должно поступать вещества примерно в 300 тысяч раз больше, если данные по метеоритному веществу не занижены. С другой стороны, наши прикидочные расчеты показывают, что в Галактике средняя плотность вещества на разных участках меняется не менее чем в 1017 раз. Эти цифры говорят о крайней неравномерности поступления вещества в Солнечную систему. Она в настоящее время как бы временно "выскочила из космических туч" в относительно чистое пространство. Поведение Солнечной системы напрямую зависит от плотности и состава этих "туч". От этого зависит как светимость Солнца, так и рост массы планет, и параметры их "возбужденного" состояния со всеми вытекающими последствиями. Несмотря на относительное метеоритное затишье, можно проверить изложенные представления по выпадению метеоритов на Землю. Орбиты искусственных спутников Земли с повышенной метеорной опасностью через три месяца станут относительно безопасными и т.п. Необходимо постоянное контролирование околоземного пространства с целью заблаговременного предупреждения о приближающихся крупных астероидах, т.к. выпадение их на Землю не столько случайность, сколько закономерность. Таким образом, будущее Солнечной системы можно прогнозировать, глядя вперед на ее путь в Галактике (конечно, и по сторонам смотреть тоже надо). В “Апокалипсисе” утверждается, что конец света будет сопровождаться звездными дождями, а, в конце концов, на землю упадет с неба большая звезда, горящая подобно светильнику - удивительно точное описание столкновения Земли с огромной периодической кометой, на орбите которой располагается рой астероидов, образовавшихся при ее разрушении под влиянием Солнца. Если столкновение с кометой к концу света не приведет, то это описание с тем же успехом может быть применено к столкновению Земли с Луной, о чем написано в следующем параграфе.
В этой связи, обратим свое внимание на Луну. Похоже, что она была захвачена в большей своей части Солнечной системой в соответствии с фигурой 20.1 и с квантовым числом 5 (как у Земли), имея большой эксцентриситет орбиты и наклон ее к плоскости эклиптики. Такой ход событий не уникален, а скорее закономерен, подтверждением чему служат такие астероиды, как Икар, Эрот, Адонис, Аполлон, Гермес. Орбита Луны быстро эволюционизировала подобно диффузии орбит комет, уменьшая эксцентриситет и наклон орбиты. В какой-то момент этой эволюции Луна была перехвачена Землей (не позднее 10 миллионов лет назад, т.к. форма Земли до сих пор помнит период более быстрого вращения вокруг оси) и новая орбита уже вокруг Земли постепенно стала круговой и в плоскости эклиптики. Луна также “помнит” этот орбитальный перехват, т.к. ее центр тяжести лежит гораздо ближе к Земле, чем это следует из нынешнего положения. “Одной из главных целей лунных исследований по-прежнему остается решение проблемы происхождения и эволюции Луны и ее связи с Землей. Предложен целый ряд гипотез происхождения и образования Луны. В частности, высказываются предположения, что Луна выделилась из мантии Земли (гипотеза отторжения), что Земля и Луна образовались одновременно как двойная планета в тесной близости друг к другу путем аккреции сходного родительского вещества (гипотеза совместного происхождения), что Луна образовалась где-то в Солнечной системе и лишь впоследствии была захвачена Землей (гипотеза захвата), наконец, что Луна образовалась путем объединения кольца планетезималей (тел промежуточной массы), некогда окружавших Землю. Пока ни одной из упомянутых гипотез нельзя безоговорочно отдать предпочтение. Однако тот факт, что возраст образцов лунных пород колеблется в пределах 4,5-3,5 млрд. лет и близок к возрасту Земли, определенному независимо, свидетельствует в пользу гипотезы совместного происхождения”. “Физика космоса”, “Советская энциклопедия”, М., 1976, стр.310-311. С точки зрения новой физики совпадение возраста Земли, Луны и метеоритов свидетельствует не о совместном их происхождении, а о том, что образование вещества в нашей области пространства во Вселенной завершилось примерно 4 млрд. лет назад. Об этом подробнее в главе, посвященной космологии.
Здесь следует отметить то обстоятельство, что, несмотря на утверждение об идентичности химсостава, особенно для двойных планет, в отношении Луны необходимо уточнение в том смысле, что ее масса недостаточна для удержания атмосферы, поэтому существование, например, жидкой воды на ней невозможно, а только во внутренних полостях или в виде льда глубоко под поверхностью в экваториальной области и ближе к поверхности на полюсах. Масса Луны растет за счет космического материала, поступающего, в основном, на обратную сторону и предназначенного для Земли, а судьба ее предрешена: из-за сильного взаимодействия в системе Земля-Луна и связанной с этим значительной диссипации энергии, несмотря на то, что в настоящее время ночное светило удаляется от нас со скоростью 3 см/год, Луна упадет на Землю, предварительно разрушившись в зоне Роша из-за приливных сил. Результаты расчетов эволюции системы Земля-Луна Джорджа Говарда Дарвина (1845-1912) - второго сына знаменитого Чарлза Дарвина: “Земные сутки на этом этапе должны постепенно стать больше 55 нынешних суток, и лунные приливные волны будут отставать от направления на Луну. Луна будет стремиться возвратить Землю в положение относительного равновесия, т.е. ускорять ее вращение, однако солнечное тяготение постепенно будет уменьшать механическую энергию Луны, которая будет затрачиваться на “раскручивание” Земли и на приливное трение. В результате Луна начнет постепенно приближаться к Земле и в конечном итоге обрушится на нее”. В.Г. Демин “Судьба Солнечной системы”, “Наука”, М., 1975, стр. 164.
Описанный механизм, по-видимому, является обычным при росте планет и спутников за счет значительных порций космического материала.
Комментарий автора к главе 20.1 Планетные системы:
1. Притяжение Солнца не влияет на орбиты спутников. Многие авторы мучаются над разрешением надуманной проблемы: почему притяжение Солнца не влияет на орбиты спутников планет? Например, сила всемирного тяготения к Солнцу для Луны в 2,2 раза больше силы тяготения к Земле. На этом основании некоторые даже сомневаются в справедливости закона всемирного тяготения. Ответ очень прост: из равенства силы притяжения спутника к Солнцу и центробежной силы, действующей на него при орбитальном движении вместе с родной планетой, получается скорость движения равной первой космической скорости на радиусе этой орбиты независимо от массы спутника. Если «убрать» планету, то движение спутника будет практически полностью повторять орбитальное движение этой планеты. (Благодарю Владимира Андреева за дискуссию по этому вопросу).
20.2. Возможный механизм формирования планетных систем
Любая галактика имеет звездное население и газо-пылевые облака. К этому можно добавить бесчисленное количество планетарных систем и тел планетных, астероидных размеров, камней, комет и ледяных тел. Официальная планетология утверждает, что планеты сформировались из газо-пылевого облака. Новая физика предполагает постепенный захват космических тел. Механизм формирования планетных систем из газо-пылевого облака в отличие от официальных представлений можно предположить другой. Таким образом, планетные системы формируются как путем захвата блуждающих космических тел, так и за счет пересечения с газо-пылевыми облаками по механизму, изложенному ниже.
При движении звезды через газо-пылевое облако с относительной скоростью
V, звезда
захватывает весь объем облака таким радиусом R, на котором V чуть меньше второй космической
скорости V: ![]() (2).
Компоненты захваченного облака (глава 21) будут иметь эксцентриситеты орбит на
расстоянии R, близкие
к 1. Постепенно орбитальные эксцентриситеты уменьшаются и орбиты превращаются в
круговые на таком радиусе каждой орбиты r на котором орбитальная скорость равна первой космической
скорости v:
(2).
Компоненты захваченного облака (глава 21) будут иметь эксцентриситеты орбит на
расстоянии R, близкие
к 1. Постепенно орбитальные эксцентриситеты уменьшаются и орбиты превращаются в
круговые на таком радиусе каждой орбиты r на котором орбитальная скорость равна первой космической
скорости v: ![]() (1).
(1).
Естественно, что пыль с размерами, соответствующими максимуму рассеяния по теории Ми будет выдуваться наружу световой радиацией звезды и покидать область захвата. Но на более мелкие и более крупные тела световая радиация не действует. При захвате газо-пылевого облака, его компоненты двигаются по самым разным орбитам, что приводит к интенсивному слипанию частиц и росту протопланетных тел. Этот процесс в планетологии называется периодом интенсивной метеоритной бомбардировки, результаты которой мы до сих пор наблюдаем на поверхности планет. Одновременно, за счет гравидинамического взаимодействия с центральной звездой, происходит выстраивание орбит в одной плоскости и реализуется «прямое» орбитальное движение (глава 22.1).
Теория захвата приводит к следующей формуле (21.4) для потенциальной
ямы тела, имеющего ![]() :
: ![]() (3), где r0 – расстояние до потенциальной ямы (круговой орбиты).
Поскольку относительная скорость звезды и газо-пылевого облака равна V, то формула (3) показывает, что потенциальные ямы
(круговые орбиты) для любых компонентов облака расположатся пропорционально
квадрату расстояния до звезды, что и наблюдается на примере Солнечной системы.
Это главный аргумент, подтверждающий изложенные представления.
(3), где r0 – расстояние до потенциальной ямы (круговой орбиты).
Поскольку относительная скорость звезды и газо-пылевого облака равна V, то формула (3) показывает, что потенциальные ямы
(круговые орбиты) для любых компонентов облака расположатся пропорционально
квадрату расстояния до звезды, что и наблюдается на примере Солнечной системы.
Это главный аргумент, подтверждающий изложенные представления.
Чтобы найти соотношение между расстоянием для максимально удаленных круговых орбит и внешней границей захвата, приравняем (1) и (2): R=2r (4). Формула (4) показывает, что дальше удвоенного расстояния до самой отдаленной круговой орбиты захват компонентов газо-пылевого облака не происходит. Например, для Солнечной системы крайней почти круговой орбитой обладает Плутон. Средняя орбитальная скорость Плутона 4,74 км/с. Следовательно, можно считать, что относительная скорость газо-пылевого облака из которого сформировались планеты была около 4,5 км/с, а Солнечная система имеет радиус, примерно, 80 а.е. (среднее расстояние Плутона от Солнца 39,44 а.е.). (Е.Н. Слюта и др. Сравнительная планетология, М., 1995, стр. 79).
Понятно, что точно по такому же принципу формируются спутниковые системы планет. Очевидно, что пересечение Солнечной системой с газо-пылевыми облаками происходило многократно с чем связаны многократные ледниковые периоды из-за «ядерной зимы» на Земле, которые, естественно, не имеют периодичности ни во времени появления, ни в продолжительности.
20.3. Возникновение магнитного поля Солнца и планет
В настоящее время возникновение магнитных полей у космических тел (Солнца и планет) связывают с работой, так называемого, гидромагнитного динамо (Физическая энциклопедия под редакцией А.М. Прохорова, М., 1988, стр. 469-470). Любые теории на эту тему исходят из обязательного наличия некоторого «затравочного» магнитного поля при движении электропроводящей среды. Механизм возникновения затравочного поля не поясняется. В дальнейшем это поле усиливается различными путями, которые не столь очевидны и в большой степени надуманы, т.к. обязательно нужен конечный результат – достаточно мощное магнитное поле. Альтернативные взгляды на возникновение магнитного поля (затравочное поле – его усиление) отсутствуют.
Мы сначала рассмотрим возникновение магнитного поля в принципе, а потом перейдем к детальному анализу.
Главными условиями возникновения магнитного поля являются конвективные движения электропроводящей среды и действие сил Кориолиса на эти потоки. На фигуре 20.3.1 показан экваториальный разрез космического тела. Стрелкой показано направление вращения.
|
|
|
|
|
|
От более горячего ядра 1 радиально наружу поднимается восходящий конвективный поток 2. При своем движении сила Кориолиса заставляет этот поток отклоняться в сторону, противоположную вращению тела. По мере охлаждения потока и замедления его движения сила Кориолиса уменьшается до нуля и возникает обратный конвективный поток 3, который отклоняется уже в сторону вращения тела. Кориолисова конвективная петля постепенно всплывает к поверхности тела, т.к. нагретый поток движется быстрей охлажденного. Поскольку градиент температуры уменьшается в радиальном направлении, то в этом направлении петли конвективных потоков становятся все меньше и, наконец, практически исчезают. Конвективные потоки за счет трения электризуются и создают магнитное поле, как рамка с током. За счет внутренних электрических разрядов электризация в значительной степени подавляется. В итоге, заряды одного знака вместе с конвективными потоками вытесняются к поверхности тела, а вновь возникающие конвективные петли вынуждены переносить заряды другого знака. В итоге суммарное магнитное поле космического тела меняет свой знак. У Солнца и планет-гигантов это происходит достаточно часто по космичесим масштабам (у Солнца через 11 лет), а для Земли этот процесс может длиться тысячелетиями из-за высокой вязкости магмы. Плоскость всех конвективных петель стремится расположиться строго перпендикулярно оси вращения тела, но гравидинамическое воздействие Солнечной системы в целом пытается повернуть их в плоскость эклиптики. В результате достигается некоторый компромисс и поэтому магнитные оси космичесих тел не совпадают с осями их вращения. Еще одна особенность конвективных петель состоит в том, что в экваториальной области они достигают максимальных размеров, а в полярных районах практически не возникают. Кроме того, начиная со средних широт и в более высокие широты наклон конвективных петель увеличивается, следовательно, они вносят уменьшающийся вклад в общее магнитное поле.
Таким образом, магнитное поле космического тела тем сильнее, чем больше температура его недр, конвекция материала и скорость вращения тела. Естественно, чем больше размеры тела, тем больше в нем конвективных петель и сильней суммарное магнитное поле. В доказательство, в таблице 20.3.1 приведена качественная характеристика магнитного поля Солнца и планет.
Таблица 20.3.1.
|
Космическое тело |
Период вращения |
Магнитное поле |
Примечание |
|
Солнце |
Ср. 25,38 сут |
Мощное |
99,866% от массы Солнечной системы |
|
Меркурий |
58,65 сут |
Заметное |
Мала масса и скорость вращения |
|
Венера |
243 сут |
Отсутствует |
Очень маленькая скорость вращения |
|
Земля |
23,93 часа |
Существенное |
Мала масса |
|
Марс |
24,62 часа |
Отсутствует |
Нет внутренней конвекции материала |
|
Юпитер |
9,84 часа |
Мощное |
Большая масса и скорость вращения |
|
Сатурн |
10,23 часа |
Мощное |
Большая масса и скорость вращения |
|
Уран |
17,24 часа |
Существенное |
Незначительная конвекция |
|
Нептун |
18,2 часа |
Сильное |
Мощная внутреняя конвекция |
В применении к Солнцу, изложенные взгляды помогают лучше понять явление солнечной активности. Каждые 11 лет новые конвективные петли приближаются к поверхности Солнца и их магнитное поле выходит наружу в виде солнечных пятен, как показано на фигуре 20.3.2.
|
|
|
|
|
|
На фигуре 20.3.2: 1 – наружная поверхность Солнца, 2 – вид сбоку конвективной петли, 3 – магнитные силовые линии конвективной петли, 4 – парные солнечные пятна разной полярности.
В главе 20.3. показано, что магнитные поля планет обусловлены возникновением петель Кориолиса при внутренней конвекции электропроводящего материала планеты. Вращение планет является следствием сохранения момента импульса. Если внутри неподвижного тела, имеющего суммарный момент импульса равный нулю, начнет что-нибудь вращаться в одну сторону, то тело в целом будет вращаться в противоположную сторону так, чтобы суммарный момент импульса оставался нулевым. Момент импульса петли Кориолиса равен произведению массы конвективного потока на его скорость движения и на эффективный радиус петли, поэтому максимальный момент импульса петли будет в экваториальном сечении планеты и постепенно уменьшается до нуля к полюсам. Все петли Кориолиса вращаются в сторону, противоположную вращению планеты. Мне не удалось найти толковое объяснение причин вращения планет. В литературе ответственность за это перекладывают на вращение гипотетического протопланетного облака и удивляются аномалиям вращения некоторых планет.
Рассмотрим подробнее скорость вращения планет Солнечной системы, представленную в таблице 20.4.1. Данные заимствованы из книги: Е.Н. Слюта и др. Сравнительная планетология, М., 1995.
Таблица 20.4.1
|
Планета |
Период вращения |
Примечание |
|
Меркурий |
58,65 суток |
|
|
Венера |
243,01 суток |
Орбитальный период 224,7 суток, поэтому вращение обратное |
|
Земля |
23,93 часа |
|
|
Марс |
24,62 часа |
|
|
Юпитер |
9,84 часа |
|
|
Сатурн |
10,23 часа |
|
|
Уран |
17,24 часа |
Вращение обратное, т.к. наклон экватора к плоскости орбиты 97,870 |
|
Нептун |
18,2 часа |
|
|
Плутон |
6,39 суток |
Конвекция отсутствует |
У Меркурия петли Кориолиса незначительны из-за большого периода вращения, поэтому магнитное поле Меркурия очень слабое. У Венеры из-за очень большого периода вращения петли Кориолиса вообще не могут возникнуть, поэтому и магнитное поле у Венеры отсутствует. У планет-гигантов большая скорость вращения из-за интенсивной внутренней конвекции в результате которой образуются петли Кориолиса с большим моментом импульса, особенно в экваториальном сечении планеты. Поэтому планеты-гиганты имеют дифференциальную скорость вращения, максимальную на экваторе и снижающуюся к полюсам. Хотя при измерениях космичесих аппаратов магнитное поле этих планет сравнимо с магнитным полем Земли, но следует учесть, что эти измерения проводятся вдали от магнитного диполя планеты, тогда, как на Земле магнитный диполь близко. Поэтому реальное магнитное поле планет-гигантов очень мощное. У Плутона большой период вращения обусловлен отсутствием внутренней конвекции.
Между тепловыделением недр планеты, конвекцией и скоростью вращения имеется положительная обратная связь. При уменьшении тепловыделения, уменьшается конвекция и скорость вращения планеты. Планеты-гиганты излучают энергии значительно больше, чем получают от Солнца, поэтому уменьшение скорости вращения им не грозит. Однако у планет земной группы тепловыделение недр постепенно истощается, поэтому они замедляют вращение. Венера в этом преуспела больше всех. Меркурий тоже существенно замедлил свое вращение. Марс по продолжительности периода вращения обогнал Землю, но и Земля постепенно замедляет вращение. Все планеты земной группы сравнительно малы, поэтому у них увеличены теплопотери в окружающее пространство. По-видимому в глубокой древности их скорость вращения была значительно больше.
20.5. Влияние внутренней конвекции на географию планет
|
|
|
|
|
|
В главе 20.3 показан механизм образования конвективных петель при внутренней конвекции материала планеты за счет действия силы Кориолиса. Движение материала в петлях Кориолиса противоположно вращению планеты. По данным Физической энциклопедии под редакцией А.М. Прохорова М., 1988 литосфера Земли имеет океаническую кору толщиной ~10 км (со слоем воды) и материковую кору толщиной до нескольких десятков километров в горных районах. Вся литосфера толщиной ~70 км и на континентах до 150-200 км плавает в жидкой астеносфере по границе Мохо. Таким образом, литосфера контактирует в нижней своей части с конвективными потоками в петлях Кориолиса. Поэтому континенты постепенно перемещаются в западном направлении под воздействием конвективных потоков, как показано на фигуре 20.5.1.
На фигуре 20.5.1: 1 – астеносфера, 2 – конвективная петля Кориолиса, 3
– океаническая кора, 4 – континент, 5 – основание горной системы.
|
|
Фиг. 20.5.3
Фиг. 20.5.2
На фигуре 20.5.2 показаны Северная и Южная Америка (белая линия – экватор). Из фигуры видно, что американский континент, как бульдозер, нагреб на фронте движения в западном направлении горные системы.
Похоже, что Австралия на фигуре 20.5.3 когда-то вообще была оторвана от Южной Америки и пересекла весь Тихий океан. На бывшем ее местообитании осталась Перуанская котловина. Как сама Австралия, так и Перуанская котловина в Южной Америке одинаково простираются по широте (10-350 ю.ш.)
Поскольку движение материала в петлях Кориолиса более интенсивное в направлении к экватору, то в северном полушарии Земли вытянутые меридионально горные системы за сотни миллионов лет воздействия конвективных потоков должны поворачиваться по часовой стрелке, а в южном полушарии – против часовой стрелки. В южном полушарии немного подтверждений этого предположения, зато в северном полушарии их достаточно. Скандинавия, Новая Земля, Уральские горы, Камчатка, о. Тайвань, Японские острова. Эти примеры показаны на фигуре 20.5.4. Вблизи экватора горные системы располагаются вдоль параллелей.
Фиг. 20.5.4
20.6. Динамика планет, атомов и элементарных частиц аналогична
Поскольку все свободные тела двигаются по винтовой траектории, нас здесь будут интересовать параметры этой траектории для разных микро- и макросистем. Эксперименты подтверждают справедливость формулы де Бройля и одинаковое значение момента импульса L элементарных частиц на винтовой траектории (глава 2.2):
![]() (20.6.1).
(20.6.1).
Из (20.6.1) легко посчитать произведение vr для траектории любой свободной элементарной частицы:
![]() (20.6.2),
(20.6.2),
где m – масса частицы. Формула (20.6.2) будет верна и для обычных атомов:
![]() (20.6.3),
(20.6.3),
где me
– масса электрона. У нормальных атомов орбитальные моменты всех электронов
одинаковы и равны ![]() (глава 13).
(глава 13).
У ридберговских атомов орбитальные моменты электронов кратны ![]() (глава
13.5):
(глава
13.5):
![]() (20.6.4),
(20.6.4),
поэтому для них постоянной величиной будет:
![]() (20.6.5),
(20.6.5),
где n – кратность момента импульса электрона или главное квантовое число его.
Для мезоатомов (глава 15.1), содержащих вместо электрона мезон, параметры его орбитальной траектории будут соответствовать формуле (20.6.2).
Из таблицы 11.2.5.1 главы 11.2.5 видно, что «стандартные» значения ![]() , где n – квантовое число
планеты (таблица 20.1) для планет Солнечной системы, примерно в 5 раз больше
для юпитерной группы планет, чем для земной группы. В то же время плотность
последних в 5 раз больше, т.е. можно записать:
, где n – квантовое число
планеты (таблица 20.1) для планет Солнечной системы, примерно в 5 раз больше
для юпитерной группы планет, чем для земной группы. В то же время плотность
последних в 5 раз больше, т.е. можно записать:
![]() (20.6.6),
(20.6.6),
где K – коэффициент пропорциональности, d – средняя плотность планеты г/см3. Для первого квантового состояния:
K=vrd (20.6.7).
По физическому смыслу (20.6.7) представляет собой удельный объемный орбитальный момент импульса планеты. Поэтому можно записать:
![]() (20.6.8),
(20.6.8),
где L – орбитальный момент импульса планеты, V – объем планеты. По формуле (20.6.8) легко найти средние плотности планет или спутников или массы этих объектов из параметров орбиты. Формулу (20.6.8) без изменения можно применять к любой частице, имея в виду, что vr – произведение скорости на радиус винтовой траектории, d – плотность частицы, L –момент импульса частицы на винтовой траектории, V – объем частицы. Разделив обе части (20.6.8) на плотность частицы, получим очевидное равенство:
L=![]() =mvr
(20.6.9).
=mvr
(20.6.9).
В главе 22.2 показано, что постоянная Планка ![]() - это
величина, обратная удельной индукции r
гравидинамического поля элементарной частицы:
- это
величина, обратная удельной индукции r
гравидинамического поля элементарной частицы:
![]() (20.6.10).
(20.6.10).
(20.6.10) подставим в (20.6.2) и заметим, что ![]() , где B – индукция
гравидинамического поля частицы:
, где B – индукция
гравидинамического поля частицы:
![]() (20.6.11).
(20.6.11).
Формула (20.6.11) имеет универсальное применение для любых тел. Таким образом, главный критерий винтового движения свободных тел (и их орбитального движения при захвате) определяется только гравидинамической индукцией тела. При движении тела в собственном гравидинамическом поле возникает аналог силы Лоренца, направленный перпендикулярно индукции гравидинамического поля.