2. О ДВИЖЕНИИ СВОБОДНОГО ЭЛЕКТРОНА И ГРАВИДИНАМИЧЕСКОМ ПОЛЕ
|
|
|
|
|
|
Обратимся к водородоподобному атому, изображенному на фигуре 2.1.
Известно, что любая система стремится к минимуму потенциальной энергии и по достижению его занимает устойчивое состояние равновесия в потенциальной яме, которое называют основным состоянием.
Для потенциальной энергии электрона можем записать (используя (1.5):
![]() (2.1).
(2.1).
Мы не должны потерять
здравый смысл, как это сделано в классическом выражении радиуса орбиты
электрона, где масса электрона стоит в знаменателе. Как известно (например,
Б.М. Яворский, А.А. Детлаф “Курс физики III”, “Высшая школа”, М., 1967,
стр.307), теория Бора приводит к следующему выражению для радиусов орбит в
водородоподобном атоме:![]() , где масса электрона стоит в знаменателе и
противоречит здравому смыслу, по которому должна стоять в числителе. Точно к
такому же выражению приводит и квантовая механика. Вразумительных объяснений
этого казуса официальная наука не приводит, а попытки таковых здесь приводить,
просто не стоит.
, где масса электрона стоит в знаменателе и
противоречит здравому смыслу, по которому должна стоять в числителе. Точно к
такому же выражению приводит и квантовая механика. Вразумительных объяснений
этого казуса официальная наука не приводит, а попытки таковых здесь приводить,
просто не стоит.
Подставим ![]() в
(2.1) и обозначим
в
(2.1) и обозначим ![]() :
:
![]() (2.2).
(2.2).
Дифференцируя (2.2) и приравнивая полученный результат нулю, что означает минимум функции (2.2), найдем значение радиуса орбиты электрона, соответствующего этому минимуму:
![]() (2.3).
(2.3).
В формуле (2.3) масса электрона заняла подобающее ей положение в числителе, а не в знаменателе аналогичного выражения по теории Бора и квантовой механике.
Подставив (2.3) в (2.2), получим энергию связи электрона с ядром:
![]() (2.4).
(2.4).
Физический
смысл величины ![]() состоит в том, что это произведение Vr
для электрона в бесконечности, т.е. присуще свободному электрону.
состоит в том, что это произведение Vr
для электрона в бесконечности, т.е. присуще свободному электрону.
Вычислим
значение ![]() из энергии ионизации
атома водорода по (2.4). Оно оказалось равным 1,1576 см2/сек,
соответственно, момент количества движения для свободного электрона составит
из энергии ионизации
атома водорода по (2.4). Оно оказалось равным 1,1576 см2/сек,
соответственно, момент количества движения для свободного электрона составит ![]() .
Естественно, что это значение останется постоянным и для водородоподобных и
других атомов в соответствии с законом сохранения момента количества движения.
Точно такое же значение момента импульса электрона мы получили бы, пользуясь
формулой для энергии связи по теории Бора или квантовой механике. Необходимо отметить, что ортодоксальная физика для момента количества
движения электрона (спина) принимает значение
.
Естественно, что это значение останется постоянным и для водородоподобных и
других атомов в соответствии с законом сохранения момента количества движения.
Точно такое же значение момента импульса электрона мы получили бы, пользуясь
формулой для энергии связи по теории Бора или квантовой механике. Необходимо отметить, что ортодоксальная физика для момента количества
движения электрона (спина) принимает значение ![]() . Неизвестно, как она будет
объяснять эту несуразицу (трудно игнорировать экспериментальное значение!), но
один этот факт способен полностью разрушить построения современной физики, т.к.
для нее (в отличие от новой физики) имеет принципиальное значение целым или
полуцелым спином обладает электрон.
. Неизвестно, как она будет
объяснять эту несуразицу (трудно игнорировать экспериментальное значение!), но
один этот факт способен полностью разрушить построения современной физики, т.к.
для нее (в отличие от новой физики) имеет принципиальное значение целым или
полуцелым спином обладает электрон.
Электрон, таким образом, находится в потенциальной яме и, вращаясь вокруг ядра, ничего не может излучать до тех пор, пока не произойдет поглощения энергии с переходом в возбужденное состояние, после растрачивания этой энергии на излучение, электрон вновь займет основное состояние.
Вот каким образом квантовая механика пытается
объяснить устойчивость атома водорода (ведь она считает, что потенциальная
энергия взаимодействия электрона с ядром атома водорода имеет вид: ![]() , т.е.
потенциальной ямы не существует, а существует потенциальная “пропасть” и
электрон обязан упасть на ядро). Цитирую по книге: “Физика микромира”,
“Советская энциклопедия”, М., 1980, стр.33:
, т.е.
потенциальной ямы не существует, а существует потенциальная “пропасть” и
электрон обязан упасть на ядро). Цитирую по книге: “Физика микромира”,
“Советская энциклопедия”, М., 1980, стр.33:
“Минимальную энергию атома водорода
можно найти с помощью соотношения неопределенностей. Это соотношение объясняет,
почему электрон не может упасть на ядро. Если электрон находится в области
размером r, то, согласно соотношению неопределенностей, разброс в
импульсах будет порядка ![]() . Связанный с этим разброс кинетической
энергии
. Связанный с этим разброс кинетической
энергии ![]() . Полная энергия электрона в атоме водорода
. Полная энергия электрона в атоме водорода ![]() .
(Заметьте, что это выражение полностью совпадает с (2.1) - В.К.). Чем ближе
электрон к ядру, тем меньше его потенциальная энергия. Но одновременно растет
кинетическая энергия электрона (~1/r2),
причем быстрее, чем убывает потенциальная (~1/r).
Приближаясь к ядру, электрон начинает двигаться настолько быстро, что упасть на
ядро не может (?!). Он будет в среднем находиться на таком расстоянии от ядра,
при котором его полная энергия окажется минимальной (?!). Это расстояние можно
найти по общим правилам
определения минимума функции”. Как видим, здесь формально сделано то же
самое, что и при выводе (2.3) и (2.4), но при этом попран не только здравый
физический и математический смысл, но и фундаментальный закон сохранения
энергии. Как бы быстро не двигался электрон вблизи ядра, судьба его вовсе не
определяется скоростью движения. Сумма потенциальной и кинетической энергии
электрона не может иметь минимум, т.к. она постоянна, что требует закон
сохранения энергии, следовательно, дифференцирование функции полной энергии -
некорректная операция. Помимо всего этого, по представлениям квантовой
механики, рассматриваемый электрон вообще не движется (S-электрон), т.к.
не обладает орбитальным моментом импульса (см. в том же источнике, стр.35 и
рис.16). Современная физика представляет собой почти сплошное “лоскутное
одеяло”, в котором каждая “заплатка” сделана подобным образом, иначе не
сводятся концы с концами.
.
(Заметьте, что это выражение полностью совпадает с (2.1) - В.К.). Чем ближе
электрон к ядру, тем меньше его потенциальная энергия. Но одновременно растет
кинетическая энергия электрона (~1/r2),
причем быстрее, чем убывает потенциальная (~1/r).
Приближаясь к ядру, электрон начинает двигаться настолько быстро, что упасть на
ядро не может (?!). Он будет в среднем находиться на таком расстоянии от ядра,
при котором его полная энергия окажется минимальной (?!). Это расстояние можно
найти по общим правилам
определения минимума функции”. Как видим, здесь формально сделано то же
самое, что и при выводе (2.3) и (2.4), но при этом попран не только здравый
физический и математический смысл, но и фундаментальный закон сохранения
энергии. Как бы быстро не двигался электрон вблизи ядра, судьба его вовсе не
определяется скоростью движения. Сумма потенциальной и кинетической энергии
электрона не может иметь минимум, т.к. она постоянна, что требует закон
сохранения энергии, следовательно, дифференцирование функции полной энергии -
некорректная операция. Помимо всего этого, по представлениям квантовой
механики, рассматриваемый электрон вообще не движется (S-электрон), т.к.
не обладает орбитальным моментом импульса (см. в том же источнике, стр.35 и
рис.16). Современная физика представляет собой почти сплошное “лоскутное
одеяло”, в котором каждая “заплатка” сделана подобным образом, иначе не
сводятся концы с концами.
Для объяснения наблюдаемых фактов, необходимо предположение о том, что свободный электрон движется по винтовой линии.
“Квантовая механика в современной трактовке исходит из того, что в принципе невозможно построение теории индивидуального микропроцесса, что возможна лишь теория статистических совокупностей - ансамблей, тождественных микрообразований”. Н.И. Карякин и др. “Краткий справочник по физике”, “Высшая школа”, М., 1962, стр.380. Рассматривая поведение отдельной частицы, квантовая механика на каждом шагу нарушает этот свой принцип.
Ниже будут раскрыты причины такого движения для любых свободных тел, в том числе и макроскопических. Тогда те значения магнитного момента электрона и спина (под которым здесь подразумевается механический момент), которые мы приписываем собственно электрону, получают другое толкование. Экспериментальные значения спина будут связаны с моментом количества движения по виткам винтовой линии, а магнитный момент будет следствием такого движения. Собственный магнитный момент и момент количества движения "неподвижного" электрона очень мал, что будет ясно в разделе, посвященном его устройству. Так просто снимается парадокс, связанный со спином электрона. Теперь электрону нет необходимости вращаться со скоростью в 300 раз превосходящей скорость света, чтобы обеспечить наблюдаемый магнитный и механический момент. Нет необходимости и в самом термине "спин", поэтому мы не будем злоупотреблять этим термином. Проглотив в свое время ядовитую пилюлю спина и отсутствия орбитального момента S-электронов, современная физика обрекла себя на верную гибель, и всякие попытки втиснуть эту проблему в рамки здравого смысла, безуспешны. В этом может убедиться каждый, взявший на себя труд не предвзято разобраться в куче противоречивых объяснений данного вопроса, не столько его проясняющих, сколько окончательно запутывающих.
Самое смешное состоит в том, что современная физика, считая спин связанным с внутренним вращением электрона, а не с моментом импульса по винтовой траектории, валит с больной головы на здоровую, утверждая ограниченность теории Бора: “Теория Бора, блестяще объяснив спектр водорода, оказалась не в состоянии объяснить свойства основного состояния атома водорода (n=1) сферически-симметричное распределение заряда (иначе будет момент импульса! - В.К.), отсутствие орбитального механического и магнитного моментов, а также совершенно непригодной к более сложным атомам, начиная с гелия”. Н.И. Карякин и др. “Краткий справочник по физике”, “Высшая школа”, М., 1962, стр.350.
Электрон,
двигаясь по винтовой линии и "одеваясь" на ядро, по закону сохранения
момента количества движения не изменит значения ![]() . Этим и объясняется
кажущееся "отсутствие" орбитального и магнитного моментов электрона в
атоме, что заставило ортодоксов с опаской говорить вообще о движении электрона
по орбите.
. Этим и объясняется
кажущееся "отсутствие" орбитального и магнитного моментов электрона в
атоме, что заставило ортодоксов с опаской говорить вообще о движении электрона
по орбите.
В опыте Штерна
- Герлаха сквозь неоднородное магнитное поле пропускался узкий пучок атомов в S-состоянии,
когда по представлениям квантовой механики орбитальный момент электрона должен
равняться нулю (электронное облако вокруг ядра сферически симметрично). При
этом на экране наблюдается не одна полоса, соответствующая нерасщепленному
пучку, а две. Измерив величину расщепления, Штерн и Герлах нашли, что магнитный
момент электрона равен одному магнетону Бора. Квантовая механика объясняет это
наличием “спина” - собственного момента импульса электрона, но при сферически
симметричном распределении электрона в атоме магнитный момент его должен всегда
иметь нулевое значение даже при наличии собственного магнитного момента у
электрона (одна полоса). С точки зрения новой физики опыт Штерна - Герлаха
подтверждает, что магнитный момент свободного электрона, движущегося по
винтовой траектории равен магнетону Бора (механический момент импульса равен ![]() ) и таким
он остается на атомной орбите в соответствии с законом сохранения момента
импульса.
) и таким
он остается на атомной орбите в соответствии с законом сохранения момента
импульса.
Здесь следует обратить внимание на "размазанность" электронов в атомах по современным представлениям. Если электроны в атоме представлены в виде электронного облака, то эти облака перекрываются в многоэлектронных атомах и в этом случае неясно, откуда каждый электрон знает, какая часть облака его. Кроме того, даже в водородоподобном атоме необходимо учесть взаимодействие разных частей облака между собой, но тогда при квантовомеханических расчетах мы не получим выражений (2.3) и (2.4), т.е. вступим в противоречие с экспериментальными данными. Если еще и учесть энергетическую сторону "размазывания" электрона и повторного "собирания" электронного облака в частицу при ионизации атома, то противоречие с экспериментом становится вопиющим. Поэтому приходится говорить о вероятности нахождения электрона в данной точке пространства (квантовая механика - это статистическая теория), рассматривая электрон все же частицей. Но тогда возникает противоречие с экспериментальными данными “отсутствия” орбитального момента импульса S-электронов, которые лучше бы представить “неподвижным” облаком. Поэтому квантовая физика способна одновременно считать электрон и частицей и “облаком” нисколько не смущаясь таким абсурдом. Применение термина «волновая функция» вместо термина «облако» в принципе ничего не меняет. В качестве примера цитата из книги К.П. Белов, Н.Г. Бочкаев, Магнетизм на Земле и в космосе, “Наука”, 1983, стр. 31: “Причины этого понятны - у большинства молекул протяженность и плотность электронного облака по разным направлениям различны”, и в следующем же абзаце: “Эти данные удается объяснить из предположения, что под действием магнитного поля в ароматических соединениях возникают замкнутые токи вдоль всей системы связей, образующей кольцо. Иными словами, часть электронов молекулы способна свободно обегать кольцо”.
Современная физика фактически отвергает научный метод познания, поскольку в зависимости от сиюминутной выгоды может пользоваться классическими представлениями или представлениями квантовой механики, рассматривать только волновую ипостась или только корпускулярные свойства частицы, с легкостью приспосабливая свои взгляды под новые экспериментальные и собственные теоретические данные. Мнение Стивена Вайнберга, американского физика-теоретика, одного из создателей единой теории электромагнитного и слабого взаимодействий: “Задача физика - выработать простой взгляд на явления природы, объяснить огромное множество сложных процессов с единой точки зрения на основе нескольких простых принципов”. “Химия и жизнь”, №4, 1983, стр.19. Этим советом современная физика не пользуется, в том числе и сам Вайнберг, быстро усложняя достаточно простые исходные гипотезы, что говорит об ошибочности исходных гипотез.
Длина волны де Бройля приобретает простой физический смысл, как шаг винтовой линии (сравните с официальной наукой).
“Если в
классической физике подразумевается, что движение каждой частицы подчиняется
детерминистическим законам и его можно точно и однозначно предсказать, а
вероятностное описание применяется к множеству частиц, для которых это сделать
сложно математически, то квантовая механика утверждает принципиальную
невозможность точного описания движения даже одной частицы. В ней волны де
Бройля нельзя даже интерпретировать, как волны вероятности, т.к. она для
некоторых точек пространства примет отрицательные значения. Как
было впервые показано Борном, возникающие здесь трудности, свидетельствующие о
глубоком различии между вероятностным описанием в классической и в квантовой
физике, можно устранить, если принять, что по волновому закону меняется не сама
вероятность, а некая величина (?!), названная амплитудой вероятности и
обозначаемая ![]() (x,y,z,t).
Эту величину называют также волновой функцией. Амплитуда вероятности должна
быть комплексной, и вероятность w пропорциональна квадрату ее модуля: w~|
(x,y,z,t).
Эту величину называют также волновой функцией. Амплитуда вероятности должна
быть комплексной, и вероятность w пропорциональна квадрату ее модуля: w~|![]() |2.
Волновая функция выступает в квантовой теории как основной носитель информации
и о корпускулярных (?!) и о волновых свойствах
системы. Предложенное Борном толкование волн де Бройля исключает их понимание
как классических волн материи. Связывая, например, со свободным электроном
плоскую волну, не нужно понимать это так, будто бы электрон “размазан” по
огромной области: в действительности это означает (?!), что
хотя электрон продолжает выступать в теории как точечный объект, вероятность
обнаружить его в любой из точек пространства одинакова”. “Физика микромира”,
“Советская энциклопедия”, М., 1980, стр.17. Как видим здесь и в дальнейшем,
современная физика предпочитает “устранять трудности” вместо пересмотра основ.
|2.
Волновая функция выступает в квантовой теории как основной носитель информации
и о корпускулярных (?!) и о волновых свойствах
системы. Предложенное Борном толкование волн де Бройля исключает их понимание
как классических волн материи. Связывая, например, со свободным электроном
плоскую волну, не нужно понимать это так, будто бы электрон “размазан” по
огромной области: в действительности это означает (?!), что
хотя электрон продолжает выступать в теории как точечный объект, вероятность
обнаружить его в любой из точек пространства одинакова”. “Физика микромира”,
“Советская энциклопедия”, М., 1980, стр.17. Как видим здесь и в дальнейшем,
современная физика предпочитает “устранять трудности” вместо пересмотра основ.
Записывая
выражение длины волны де Бройля через поступательную скорость ![]() частицы
и длины окружности через тангенциальную скорость V:
частицы
и длины окружности через тангенциальную скорость V:
![]() (2.5),
(2.5),
где T - период обращения.
![]() (2.6),
(2.6),
найдем:
![]() (2.7).
(2.7).
Умножив обе части (2.7) на V, получим:
![]() (2.8).
(2.8).
Вспомнив, что
экспериментальное значение механического момента, определенное по энергии связи
электрона с ядром составляет ![]() , откуда:
, откуда:
![]() (2.9).
(2.9).
Сравнивая (2.9) и (2.8), приходим к выводу, что свободная частица движется таким образом, что ее поступательная и тангенциальная скорость по витку винтовой линии равны. Этот вывод является следствием принципа равного распределения энергии по степеням свободы. Тогда из (2.7) следует, что радиус витка винтовой линии обратно пропорционален поступательной скорости частицы:
![]() (2.10).
(2.10).
Записывая: ![]() и
разделив обе части на
и
разделив обе части на ![]() , получим:
, получим: ![]() , где:
, где: ![]() , а
, а ![]() ,
поэтому:
,
поэтому:
![]() (2.11).
(2.11).
Этот результат говорит о том, что длина волны
де Бройля равна длине окружности нормального сечения винтовой линии или длине
орбиты, в случае связанной частицы. В квантовой механике считают, что на
устойчивой орбите в атоме укладывается целое число волн де Бройля (“Физика
микромира”, “Советская энциклопедия”, М., 1980, стр.121). При этом, во-первых,
противоречат собственным представлениям (это утверждение можно сформулировать
так: “на устойчивой орбите укладывается целое число амплитуд вероятности”, что
явная чушь). Во-вторых, входят в противоречие с законом сохранения момента
импульса, т. к. считают его кратным ![]() . Новая физика строго чтит
фундаментальные законы, поэтому знает, что с любым телом связана только одна
волна де Бройля, а длина ее зависит от скорости движения. Дискретность
состояний электрона в возбужденном атоме она объясняет другими причинами.
. Новая физика строго чтит
фундаментальные законы, поэтому знает, что с любым телом связана только одна
волна де Бройля, а длина ее зависит от скорости движения. Дискретность
состояний электрона в возбужденном атоме она объясняет другими причинами.
Таким образом, все параметры винтовой линии, по которой движутся свободные частицы, мы определили.
В формуле де
Бройля: ![]() постоянной Планка фактически нет. В
числителе стоит момент количества движения частицы по винтовой линии. Он
одинаков для разных частиц, что подтверждают эксперименты, поэтому официальное
пользование этой формулой для определения длины волны частицы в зависимости от
ее массы некорректно. Эта формула даст правильные значения
длины волны де Бройля только для частиц с одинаковым моментом импульса на
винтовой траектории и равным
постоянной Планка фактически нет. В
числителе стоит момент количества движения частицы по винтовой линии. Он
одинаков для разных частиц, что подтверждают эксперименты, поэтому официальное
пользование этой формулой для определения длины волны частицы в зависимости от
ее массы некорректно. Эта формула даст правильные значения
длины волны де Бройля только для частиц с одинаковым моментом импульса на
винтовой траектории и равным ![]() . Например, новая физика считает, что момент
импульса электрона и фотона одинаков и равен
. Например, новая физика считает, что момент
импульса электрона и фотона одинаков и равен ![]() , а официальная физика,
соответственно,
, а официальная физика,
соответственно, ![]() и
и ![]() . Тем не менее, для расчета
длины волны электрона официальная физика подставляет в формулу де Бройля не
. Тем не менее, для расчета
длины волны электрона официальная физика подставляет в формулу де Бройля не ![]() , а
, а ![]() и
получает, естественно, правильное значение длины волны. Этим она
подрывает собственные основы, базирующиеся на полуцелом спине электрона. Этот
вопрос может быть достаточно легко разрешен экспериментально для других частиц,
сравнивая опытную массу, "спин" и длину волны со значением,
полученным из формулы де Бройля. Как будет показано в теории элементарных
частиц, их масса зависит от суммарного значения момента импульса компонентов. А
для макротел формулой де Бройля можно пользоваться только при том условии, если
мы в числитель будем подставлять огромный момент импульса этих тел. При этом
получим длину волны де Бройля космических масштабов, а не мизерную, какую
получает официальная физика, не понимая физического смысла формулы де Бройля.
и
получает, естественно, правильное значение длины волны. Этим она
подрывает собственные основы, базирующиеся на полуцелом спине электрона. Этот
вопрос может быть достаточно легко разрешен экспериментально для других частиц,
сравнивая опытную массу, "спин" и длину волны со значением,
полученным из формулы де Бройля. Как будет показано в теории элементарных
частиц, их масса зависит от суммарного значения момента импульса компонентов. А
для макротел формулой де Бройля можно пользоваться только при том условии, если
мы в числитель будем подставлять огромный момент импульса этих тел. При этом
получим длину волны де Бройля космических масштабов, а не мизерную, какую
получает официальная физика, не понимая физического смысла формулы де Бройля.
Формула де
Бройля ![]() доказывает,
что свободные микрочастицы двигаются не прямолинейно и
равномерно, а по винтовой линии. Действительно, умножим обе части этого
уравнения на
доказывает,
что свободные микрочастицы двигаются не прямолинейно и
равномерно, а по винтовой линии. Действительно, умножим обе части этого
уравнения на ![]() , где
, где ![]() - частота волны де Бройля, тогда получим:
- частота волны де Бройля, тогда получим: ![]() . Но
. Но ![]() это
скорость распространения волны, связанной с частицей, которая равна скорости
самой частицы. Тогда:
это
скорость распространения волны, связанной с частицей, которая равна скорости
самой частицы. Тогда: ![]() . Очевидно, что в полученном равенстве обе его
части обозначают полную энергию частицы. Но по представлениям официальной
физики полная энергия прямолинейно движущейся свободной частицы равна ее кинетической энергии
. Очевидно, что в полученном равенстве обе его
части обозначают полную энергию частицы. Но по представлениям официальной
физики полная энергия прямолинейно движущейся свободной частицы равна ее кинетической энергии ![]() и еще такую же брать
негде. Следовательно, кинетическая энергия частицы складывается из
поступательного и тангенциального движения ее по винтовой траектории.
и еще такую же брать
негде. Следовательно, кинетическая энергия частицы складывается из
поступательного и тангенциального движения ее по винтовой траектории.
Теперь выясним причины, заставляющие свободные частицы двигаться по винтовой линии. Сначала проведем аналогию. Известно, что в однородном магнитном поле электрический заряд, в общем случае, движется по винтовой линии, ось которой совпадает с направлением магнитного поля. Если электрический заряд заставить вращаться вокруг оси и если он не точечный, то образующееся магнитное поле заменяет внешнее с тем же результатом. Современная физика по многим причинам считает электрон точечным (там же, стр. 479), иначе возникает масса противоречий, хотя и сам этот факт противоречит классическому значению радиуса электрона - фундаментальной физической константе. С другой стороны, точечность электрона приводит к другим неразрешимым противоречиям, связанным с бесконечностями.
С одной стороны утверждают, что представление о точечности элементарных частиц тесно связано с предположением о возможности сколь угодно точного измерения расстояний и промежутков времени, с другой стороны вводят понятие фундаментальной длины, чтобы уйти от бесконечно больших значений (например, энергия поля для точечных частиц) – расходимостей и тут же утверждают, что введение фундаментальной длины скрывает за собой неточечность частиц (Физика микромира, М., 1980, стр.197). Таким образом, понятие фундаментальной длины становится вовсе излишним, т.к. возможность точного измерения расстояний и промежутков времени не зависит от размеров частиц.
С увеличением скорости движения уменьшается радиус и шаг винтовой линии. В формулах, определяющих параметры винтового движения свободного электрона отсутствует электрический заряд, но есть гравитационный заряд (масса). Если мы попытаемся объяснить винтовое движение электрона только наличием магнитного взаимодействия, связанного с движением электрического заряда, то убедимся, что это взаимодействие очень слабо и не может вызвать такого движения. На его счет можно отнести только эффекты второго порядка. Остается единственное разумное предположение. Аналогично тому, как движущийся электрический заряд образует магнитное поле, а при его торможении излучаются фотоны, движущийся гравитационный заряд будет образовывать гравидинамическое поле - аналог магнитного поля, а при его торможении излучаются гравитоны. Ниже мы убедимся в том, что гравитон в отдельности не существует, его функции полностью исчерпываются фотоном.
Чтобы гравидинамическое взаимодействие сделать ощутимым, кроме большой скорости собственного вращения, нужен большой "гравитационный ток", равный произведению массы частицы на скорость ее перемещения, т.е. импульсу. Изучение взаимодействия гироскопов должно ответить на возникающие в связи с образованием гравидинамического поля вопросы. (Нелегальные исследователи так называемых “торсионных полей” фактически этим и занимаются). Искусственные спутники Земли тоже хорошие модели, только не надо стабилизировать их от собственного вращения, а наоборот, сильней раскрутить. Пока же будем пользоваться аналогией с магнитным полем. Гравидинамическое взаимодействие становится ощутимым в макромире из-за больших масс и, в некоторых случаях, больших скоростей движения, а в микромире его вызывают огромные скорости движения, близкие к световым. Как мы увидим позднее, гравидинамическое поле увеличивает свою интенсивность не пропорционально скорости, а аналогично тому, как растет масса при приближении скорости к световой. Поэтому все свободные частицы микромира (как потом увидим, и макромира тоже) движутся по винтовой линии, в первом приближении, независимо от электрического заряда. Исследователи “торсионного” поля фактически имеют дело с гравидинамическим.
При движении
по винтовой линии частица находится в потенциальной яме, поэтому энергия
универсального отталкивания и энергия связи равна половине энергии притяжения: ![]() , откуда
, откуда ![]() , а
гравидинамическая сила притяжения к оси винтовой траектории всегда равна
центробежной силе:
, а
гравидинамическая сила притяжения к оси винтовой траектории всегда равна
центробежной силе: ![]() .
.
Таким образом, мы можем сделать важнейший вывод: корпускулярно-волновой дуализм тел есть движение тел по винтовой линии.
Соотношения неопределенностей Гейзенберга и уравнение Шредингера являются краеугольными камнями современной физики. Посмотрим, что они представляют собой с точки зрения новой физики.
Поскольку микрочастицы движутся по
винтовой линии с вектором момента импульса, направленным вдоль движения и
равным ![]() ,
причем тангенциальная скорость движения равна поступательной, мы можем выяснить
физический смысл соотношения неопределенностей Гейзенберга.
,
причем тангенциальная скорость движения равна поступательной, мы можем выяснить
физический смысл соотношения неопределенностей Гейзенберга.
Соотношение неопределенностей
Гейзенберга получается следующим образом (см., например, Б.М. Яворский, А.А.
Детлаф “Курс физики III”, “Высшая школа”, М., 1967, стр.270-271). Ограниченная
пространственная протяженность ![]() x некоторого цуга волн связана с
наличием у него принципиальной немонохроматичности -
неизбежного наличия у такого цуга определенного интервала
x некоторого цуга волн связана с
наличием у него принципиальной немонохроматичности -
неизбежного наличия у такого цуга определенного интервала ![]()
![]() возможных частот или
интервала
возможных частот или
интервала ![]() k волновых чисел монохроматических
волн, составляющих этот цуг. Между
k волновых чисел монохроматических
волн, составляющих этот цуг. Между ![]() x и
x и ![]() k
существует связь:
k
существует связь: ![]() (a). Это соотношение справедливо для любых волновых
процессов. Для волны де Бройля частицы, движущейся вдоль оси x с
импульсом px = p (py=pz=0)
и учитывая, что px = k
(a). Это соотношение справедливо для любых волновых
процессов. Для волны де Бройля частицы, движущейся вдоль оси x с
импульсом px = p (py=pz=0)
и учитывая, что px = k![]() , имеем:
, имеем: ![]() (b). Подставив (b) в (a), найдем:
(b). Подставив (b) в (a), найдем: ![]() .
Рассматривая движение частицы вдоль осей y и z, получим
аналогичные соотношения.
.
Рассматривая движение частицы вдоль осей y и z, получим
аналогичные соотношения.
|
|
|
|
|
|
Вдоль оси Z винтовой линии траектории частицы мы увидим окружность,
изображенную на фигуре 2.2.
Запишем выражение для момента импульса частицы относительно оси винтовой траектории:
![]() (2.12).
(2.12).
Проекция вектора скорости V , например, на ось X меняется от нуля до V , поэтому:
![]() Vx=V
(2.13),
Vx=V
(2.13),
а проекция радиус-вектора r меняется от r до нуля, поэтому:
![]() x=r
(2.14).
x=r
(2.14).
Подставляя
(2.14) и (2.13) в (2.12) и учитывая, что m![]() Vx=
Vx=![]() Px
представляет собой проекцию импульса частицы на ось X, получим:
Px
представляет собой проекцию импульса частицы на ось X, получим: ![]() . При
реальных измерениях это произведение будет всегда больше
. При
реальных измерениях это произведение будет всегда больше ![]() , т.е.
соответствовать соотношению неопределенностей Гейзенберга:
, т.е.
соответствовать соотношению неопределенностей Гейзенберга:
![]() (2.15).
(2.15).
Из вывода (2.15) совершенно ясно, что это просто другая запись формулы (2.12), т.е. соотношение неопределенностей Гейзенберга – фикция. Это закон сохранения момента импульса и ничего более. Знак «больше» в формуле (2.15) – скрытое нарушение этого закона и появился от непонимания сущности закона сохранения импульса или от большого желания расширить поле научных спекуляций.
“Квантовая механика, позволяя вычислять лишь вероятности, является теорией статистической. Для проверки ее выводов необходимо иметь дело с очень большим числом тождественных систем, так называемых квантовых ансамблей” (Н.И Карякин и др. “Краткий справочник по физике”, “Высшая школа”, М., 1962, стр.382).
Физическая сущность приведенного математического упражнения состоит в том, что мы картину движения одной частицы заменили статистической картиной движения вдоль оси Z множества частиц с разной фазой движения.
В этом случае нахождение конкретной частицы в любой точке траектории равновероятно. Поэтому, если мы в эксперименте будем фотоны (электроны) один за другим пропускать через дифракционную решетку (кристалл) строго по одной линии и в одной фазе движения, то вместо общей дифракционной картины на экране, когда каждый фотон (электрон) попадает с разной вероятностью в разные места экрана, мы будем наблюдать попадание частиц в одно и то же место экрана и детерминизм в науке вновь восторжествует!
Цитата из книги А.И. Вейник “Термодинамика”, “Вышэйшая школа”, Минск, 1968, стр.435: “Приходится поражаться титанической интуиции Эйнштейна, более 30 лет боровшегося с тем направлением развития, которое приняла квантовая механика при его жизни: “...я ... беспрестанно искал другой путь для решения квантовой загадки... Эти поиски обусловлены глубокой, принципиального характера неприязнью, которую мне внушают основы статистической квантовой теории”. Эйнштейн выступал против принципа неопределенности, за детерминизм, против той роли, которую в квантовой механике отводят акту наблюдения (влиянию измерительного прибора), и т.д., вследствие чего был даже отвергнут некоторыми своими друзьями. В 1947 году он писал Максу Борну: “В наших научных взглядах мы развились в антиподы. Ты веришь в играющего в кости бога, а я - в полную закономерность в мире объективно сущего...”, “В чем я твердо убежден, так это в том, что, в конце концов, остановятся на теории, в которой закономерно связанными будут не вероятности, но факты...””.
Из вывода (2.15) ясно, что если мы не знаем начальной фазы движения электрона, мы не сумеем в любой момент сказать, где находится электрон в плоскости, перпендикулярной оси винтовой траектории. Зато, зная скорость его движения, совершенно точно определим пройденный электроном путь по оси (Z) винтовой траектории. Современная физика относительно неопределенности движения электрона в плоскости, перпендикулярной направлению движения вообще не может сказать ничего вразумительного. Соотношением неопределенностей Гейзенберга она фактически записывает момент количества движения по направлению движения, т.е. электрон при движении “кувыркается через голову” и надо как-то объяснять этот физический абсурд. Тут есть и математический абсурд - движение тела с моментом импульса возможно, по крайней мере, сразу по двум координатам (в плоскости), а не по одной линии.
Система в
основном состоянии может существовать бесконечно долго, поэтому по соотношению
неопределенностей ![]() E=0 в этом состоянии. Поэтому в основном состоянии
E=0 в этом состоянии. Поэтому в основном состоянии ![]() x
x![]() 0, а импульс
0, а импульс ![]() p
p![]()
![]() . Поскольку
энергия частицы непосредственно связана с ее импульсом, то
. Поскольку
энергия частицы непосредственно связана с ее импульсом, то ![]() E
E![]()
![]() , т.е. разброс
энергии в основном состоянии должен быть равен нулю и одновременно
неограниченно велик. Этот пример противоречия говорит о том, что истинный
физический смысл соотношения неопределенностей современной физике неведом.
, т.е. разброс
энергии в основном состоянии должен быть равен нулю и одновременно
неограниченно велик. Этот пример противоречия говорит о том, что истинный
физический смысл соотношения неопределенностей современной физике неведом.
Подводя итог сказанному, можно отметить, что новая физика имеет больше прав, чем ортодоксальная, на соотношения неопределенностей Гейзенберга, т.к. она раскрывает их подлинный физический смысл, одновременно сильно ограничивая их применение. Движение свободных тел не по прямой, а по винтовой линии и есть тот самый “скрытый параметр”, о котором мечтал Эйнштейн, чтобы покончить с принципом неопределенности.
“Если когда-либо будет доказано, что принцип неопределенности неверен, то мы должны будем ожидать полной перестройки физической теории”. Дж. Б. Мэрион,” Физика и физический мир”, Мир, М., 1975, стр. 609.
Если неопределенности Гейзенберга
являются результатом статистического рассмотрения движения частиц разной фазы
вдоль оси их винтовой траектории, то уравнение Шредингера будет результатом
такого же рассмотрения с любого направления, перпендикулярного оси траектории.
Поскольку тангенциальная скорость в точности равна поступательной скорости
частицы, проекция траектории на любую плоскость, параллельную оси траектории,
будет синусоидой, масштаб которой обратно пропорционален этой скорости. В
целом, уравнение Шредингера не может быть выведено из каких-либо законов
физики, поэтому само считается “законом”. Уравнение Шредингера для электрона в
одномерном случае (когда потенциальная энергия P и функция ![]() не
зависят от координат Y и Z):
не
зависят от координат Y и Z): ![]() , где
, где ![]() - неизвестно
что и является функцией координаты x и времени t. Квадрат
абсолютной величины ее |
- неизвестно
что и является функцией координаты x и времени t. Квадрат
абсолютной величины ее |![]() |2 является плотностью
вероятности нахождения электрона в данной области пространства,
|2 является плотностью
вероятности нахождения электрона в данной области пространства, ![]() , h
- постоянная Планка, m - масса электрона.
, h
- постоянная Планка, m - масса электрона.
Основная часть этого уравнения может быть получена из уравнения распространения гармонического колебания, в которое втиснули кинетическую энергию частицы и добавили формулу де Бройля, описывающую волновые свойства частиц, полагая, что таким примитивным образом можно разрешить проблему корпускулярно-волнового дуализма. Шредингер добавил к этому винегрету еще и потенциальную энергию частицы, сделав его “законом”. На перечисленных основаниях, ортодоксальная физика считает уравнение Шредингера полностью исчерпывающим корпускулярно-волновой дуализм частиц, хотя, фактически, оно описывает только волновую ипостась этого дуализма, несмотря на то, что в него входит масса частицы. “Незаконность” массы частицы в этом уравнении наглядно проявляется в релятивистской области скоростей, где m является функцией скорости. Если эту функцию поставить вместо массы в уравнение Шредингера, то оно станет неприменимым. Для этого случая уравнение Шредингера заменяют уравнением Дирака, которое является результатом принципиально другой теории. Кроме того, уравнение Шредингера принципиально неприменимо к движению отдельной частицы, т.к. вовсе не может предсказать ее движение (например, при дифракции на щели отдельных электронов), поэтому дает только статистическое описание поведения большого числа частиц. На это обстоятельство предпочитают закрывать глаза, описывая “движение” отдельного электрона, например, в атоме. Добавив сюда возможность получения решения уравнения Шредингера только для некоторых простейших случаев, вызывает удивление утверждение ортодоксальной физики, что уравнение Шредингера, в принципе, правильно описывает любые случаи движения частиц. “Точное решение (уравнения Шредингера) существует лишь для очень простых задач, например, гармонический осциллятор, атом водорода. Но и они требуют очень сложных математических методов вычисления. Решение более сложных задач оказывается практически невозможным”. Н.И. Карякин и др. “Краткий справочник по физике”, “Высшая школа”, М., 1962, стр. 411. Указанный пессимизм усугубляется тем, что уравнение Шредингера не совместимо с преобразованиями Лоренца, т.е. противоречит теории относительности.
Квантовая физика не может описать движение электрона вокруг ядра (как частицы ограниченной в пространстве) и вынуждена рассматривать “электронное облако” (волновую функцию). В этом случае получаются два варианта анализа, оба противоречащих экспериментальным данным. Если электрон “размазывается” в облако, то в этом случае энергия, выделяющаяся при образовании атома водорода должна быть значительно больше энергии ионизации атома, т.к. при ионизации придется собирать “облако” в одну частицу, преодолевая кулоновское отталкивание частей облака между собой. Эксперименты показывают, что энергия ионизации атома в точности равна энергии, выделяющейся при его образовании. Кроме этого, в процессе образования и ионизации атома, мы будем наблюдать нарушение закона сохранения энергии. По второму варианту электрон можно оставить корпускулой, но вероятность найти его на сколь угодно большом расстоянии от ядра отлична от нуля, тем более на таком расстоянии, где тепловая энергия электрона сравнима с энергией связи с ядром. В этом случае мы должны наблюдать самопроизвольную ионизацию газа и работа детекторов ионизирующего излучения станет невозможной. А если учесть и “туннельный” эффект (в трактовке квантовой физики), то не только самопроизвольная ионизация неотвратима, но и все линии спектров должны быть совершенно замазаны. Таким образом, механическое смешение корпускулярных и волновых свойств в одном уравнении не решают проблему корпускулярно-волнового дуализма микрочастиц. Трагедия современной физики состоит в том, что она вынуждена сидеть сразу на двух стульях: пользоваться классическими представлениями о частице, как ограниченном в пространстве физическом теле и одновременно о частице, как волне - не ограниченном в пространстве колебательном процессе. При этом, не имея ясного представления, что же такое корпускулярно-волновой дуализм частиц, физика вынуждена пользоваться той или иной стороной корпускулярно-волнового дуализма, исходя не из критерия объективности, а из критерия “выгодности”.
Движение частиц по винтовой линии с любой стороны, перпендикулярной оси этой линии, представляется, как монохроматическая волна, распространяющаяся по направлению поступательного движения частицы. Производя с этой волной те же манипуляции, что и при “выводе” уравнения Шредингера, мы получим именно его. Это дает основания все действительные достижения современной физики (очищенные от мнимых) с полным правом приписать и новой физике. Квантовая физика в современном виде требует коренного пересмотра, что доказывается многочисленными безуспешными попытками “оквантовать” гравитацию. То есть, новая физика переходит в квантовую механику, если смотреть на движение частиц не в “корень”, а сбоку и вольно обращаться с математикой.
Официальная физика
считает, что квантовая механика переходит в классическую механику в случае,
когда длина волны де Бройля стремится к нулю. Это возможно, когда формально
постоянная Планка h![]() 0.
При этом уравнение Шредингера переходит в уравнение движения классической
механики, а соотношение неопределенностей теряет свою ограничительную силу.
(Физика микромира, М., 1980, стр.384). Физический смысл нулевого значения
момента импульса частицы означает, что равна нулю ее масса или скорость или
радиус траектории.
0.
При этом уравнение Шредингера переходит в уравнение движения классической
механики, а соотношение неопределенностей теряет свою ограничительную силу.
(Физика микромира, М., 1980, стр.384). Физический смысл нулевого значения
момента импульса частицы означает, что равна нулю ее масса или скорость или
радиус траектории.
С точки зрения новой физики уменьшение длины волны де Бройля равносильно уменьшению радиуса винтовой траектории и ее шага, т.е. увеличению энергии частицы. При длине волны де Бройля стремящейся к нулю, масса и энергия тела стремятся к бесконечно большой величине при одном и том же значении момента импульса. Поскольку все свободные тела движутся по винтовой линии, то полностью отнять у них момент импульса физически невозможно, хотя при полном его отсутствии они стали бы классическими. Поэтому с официальной физикой можно согласиться, что движение частицы станет классическим при формальном стремлении постоянной Планка к нулю, только понимая под этой постоянной момент импульса частицы. С другой стороны, классическое прямолинейное движение макротела можно рассматривать как движение этого тела по окружности с бесконечно большим радиусом, т.е. с бесконечно большой длиной волны де Бройля. При этом момент импульса такого тела будет бесконечно большим, но энергия и масса могут принимать любое конечное значение. Обычные макротела имеют длину волны де Бройля космических масштабов, поэтому до релятивистских скоростей их движение можно считать практически классическим. Таким образом, строгий переход от новой физики к классической возможен, а для квантовой механики нет. Доктор М. Л. Клебанов в частном письме автору дал прекрасный анализ первого закона Ньютона: «Кроме того, в соответствии с нормальной физической логикой необходимо пересмотреть первый закон Ньютона о движении свободных тел в пустом пространстве. Это закон движения математической точки в математическом пустом пространстве. Физиком Ньютоном закон Инерции сформулирован как закон очевидности, закон конкретного опыта. И если пустое физическое пространство ещё можно как-то отождествить с математическим пустым пространством, то свободное тело никак нельзя отождествить с математической точкой, и нельзя его признать свободным, т.к. оно обладает массой не свободной от самой себя».
Современная физика и квантовая механика, в частности, не утруждают себя поиском внутренних противоречий и самокритикой. Приведу лишь один пример, показывающий, что современная квантовая механика совершенно непригодна для описания атомов. Как известно, ортодоксальные представления исходят из того, что поведение электрона в атоме определяет вид волновой функции, определяющей вероятность нахождения электрона в том или ином месте пространства вокруг ядра. Поскольку любая волновая функция перекрывает значительное расстояние в радиальном направлении, то электрон в разных местах, разрешаемых волновой функцией, обладает разной энергией. При переходе электрона с одного энергетического уровня на другой он фактически из одного случайного места одной волновой функции (случайное значение энергии) переходит в другое случайное место второй волновой функции. При этом атом должен излучать или поглощать фотоны не строго определенной энергии, а мы должны наблюдать широкие полосы поглощения или излучения, что противоречит опыту – спектральные линии очень узкие. На основании только этого противоречия необходимо отвергнуть все теоретические построения современной квантовой механики.
Описанная гипотеза о движении свободных частиц по винтовой линии является единственной и основной в этой работе. Вместе с изложенными уточнениями о движении тел по окружности, этого достаточно, чтобы произвести коренной пересмотр наших представлений, малая часть которого изложена в этой книге.
Комментарии автора к главе 2.
1. Формула де Бройля и
постоянная Планка. Ортодоксы
не понимают физического смысла ни формулы де Бройля, ни постоянной Планка.
Формула де Бройля – обыкновенная тождественная запись момента импульса тела.
Запишем это тождество: mVr=mVr (1.1). Правую часть (1.1) заменим
на постоянную Планка ![]() : mVr=
: mVr=![]() (1.2).
Умножим обе части (1.2) на 2
(1.2).
Умножим обе части (1.2) на 2![]() :
: ![]() mV=h. В
итоге мы получили формулу де Бройля:
mV=h. В
итоге мы получили формулу де Бройля: ![]() =h/mV.
Отсюда следует, что постоянная Планка – обычный момент импульса частиц на
винтовой траектории и у всех частиц он имеет одинаковое значение. Яркий пример
непонимания ортодоксами смысла формулы де Бройля состоит в том, что они в
знаменатель этой формулы подставляют массу макротел, получают невероятно малую
длину волны де Бройля и тем «доказывают» отсутствие у макротел волновых
свойств.
=h/mV.
Отсюда следует, что постоянная Планка – обычный момент импульса частиц на
винтовой траектории и у всех частиц он имеет одинаковое значение. Яркий пример
непонимания ортодоксами смысла формулы де Бройля состоит в том, что они в
знаменатель этой формулы подставляют массу макротел, получают невероятно малую
длину волны де Бройля и тем «доказывают» отсутствие у макротел волновых
свойств.
2. Подлог – надежный прием официальной физики.
Здесь придется вновь повторить цитату, приведенную в главе 2: “Физика микромира”, “Советская энциклопедия”, М., 1980, стр.33:
«Минимальную энергию
атома водорода можно найти с помощью соотношения неопределенностей. Это
соотношение объясняет, почему электрон не может упасть на ядро. Если электрон
находится в области размером r (1), то, согласно соотношению неопределенностей,
разброс в импульсах будет порядка ![]() (2). Связанный с этим разброс кинетической
энергии
(2). Связанный с этим разброс кинетической
энергии ![]() (3). Полная энергия электрона в атоме водорода
(3). Полная энергия электрона в атоме водорода ![]() (4)».
(4)».
По соотношению
неопределенностей нельзя указывать точный размер области нахождения электрона r
(1), но только ![]() r, которое надо вставить и в (2), иначе
импульс (и энергия) электрона станут бесконечно большими. Тогда в (3) и (4)
вместо r будет
r, которое надо вставить и в (2), иначе
импульс (и энергия) электрона станут бесконечно большими. Тогда в (3) и (4)
вместо r будет ![]() r и приведенные
выкладки теряют всякий смысл. Таким образом, посредством подлога:
r и приведенные
выкладки теряют всякий смысл. Таким образом, посредством подлога: ![]() r
r ![]() r получают то, что хотят получить.
r получают то, что хотят получить.
2.1. Винтовое движение микрочастиц
В связи с вопросами читателей, придется более подробно рассмотреть винтовое движение микрочастиц и причины такого движения на примере электрона.
Момент импульса электрона на орбите Бора равен произведению его массы на скорость орбитального движения (в 137 раз меньше скорости света) и на радиус орбиты Бора. В результате получим значение механического момента электрона при орбитальном движении равное постоянной Планка в виде:
![]() (2.1.1).
(2.1.1).
Теперь удалим электрон из атома. Как будет двигаться свободный электрон? Очевидно, что он будет иметь некоторую кинетическую энергию поступательного движения, но его механический момент останется тем же самым, т.е. он будет двигаться по винтовой траектории:
![]() (2.1.2),
(2.1.2),
где: me – масса электрона, V – тангенциальная скорость на витках траектории, r – радиус витка.
Закон сохранения механического момента тела имеет такой же высокий статус, как и закон сохранения энергии, поэтому он гарантирует винтовую траекторию в любом случае. На этой траектории произведение Vr остается постоянным, что видно из (2.1.2).
Таким образом, механический момент электрона по формуле (2.1.1), который ортодоксы называют «спин» и принимают для него значение в 2 раза меньше, чем по (2.1.1), никакого отношения к собственному механическому моменту электрона не имеет, а относится к его винтовой траектории. Собственный механический момент электрона найдем в результате перемножения массы электрона на скорость света с которой он вращается вокруг собственной оси и на классический радиус электрона. В результате получим значение в 137 раз меньше орбитального момента или момента на витках винтовой траектории:
![]() (2.1.3),
(2.1.3),
где ![]() - постоянная тонкой структуры. Поэтому электрон всегда имеет
два постоянных механических момента, но, к сожалению, об этом официальная
физика не догадывается.
- постоянная тонкой структуры. Поэтому электрон всегда имеет
два постоянных механических момента, но, к сожалению, об этом официальная
физика не догадывается.
Причину винтового движения легко понять, сравнивая движение электрического заряда перпендикулярно внешнему магнитному полю и движение гравитационного заряда перпендикулярно собственному гравидинамическому полю. В обеих случаях заряд движется по окружности под действием силы Лоренца или его гравидинамического аналога, направленных к центру окружности. Разница только в том, что вращающийся со скоростью света электрон создает вдоль собственной оси вращения максимально возможную напряженность гравидинамического поля (глава 11.1) и гравидинамическое взаимодействие становится в 4,17×1043 раз сильней гравитационного и не имеет равных в природе. Поэтому гравидинамический аналог силы Лоренца имеет такую величину, что заставляет электрон двигаться по винтовой траектории с Vr=1,1576 см2/сек.
2.2. Экспериментальные доказательства винтового движения
Хочу доставить дополнительное удовольствие тем злым языкам, которые издевались над моим утверждением, что приводить экспериментальные доказательства винтового движения не требуется – их и так достаточно. Здесь я повторяю этот тезис, тем более, что в моей глухой деревне можно проводить только мысленные эксперименты. Для правильных выводов из накопленных экспериментальных данных не нужен длинный язык, нужен хотя бы короткий ум.
Ниже приведу доказательства винтового движения свободных тел в произвольном порядке.
1. Из многочисленных экспериментов известно, что «волна де Бройля» для любых микрочастиц определяется одной и той же формулой:
![]() (2.2.1).
(2.2.1).
Если разделить
обе части этой формулы на 2![]() , то она примет вид:
, то она примет вид:
![]() (2.2.2),
(2.2.2),
где ![]() -
уже нельзя назвать «квантом действия» - это обычный момент импульса частицы,
который, судя по экспериментам у всех частиц одинаков (эту величину называют
«спин» те, кто не знает ее физического смысла, а кто пытается это выяснить,
ясности из научной литературы не получит). По определению момента импульса r обозначает радиус
кругового движения частицы со скоростью V, но с такой же скоростью частица двигается поступательно,
т.е. в целом движение представляет винтовую траекторию.
-
уже нельзя назвать «квантом действия» - это обычный момент импульса частицы,
который, судя по экспериментам у всех частиц одинаков (эту величину называют
«спин» те, кто не знает ее физического смысла, а кто пытается это выяснить,
ясности из научной литературы не получит). По определению момента импульса r обозначает радиус
кругового движения частицы со скоростью V, но с такой же скоростью частица двигается поступательно,
т.е. в целом движение представляет винтовую траекторию.
2. Численная
величина ![]() очень большая, чтобы ее можно было бы
отнести к собственному вращению частицы, поэтому хитрые ортодоксы и назвали ее
«спин». Момент импульса вращающегося вокруг собственной оси электрона
(собственный момент импульса) найдем, аналогично (2.2.2), умножив массу
электрона на его скорость вращения (равную скорости света) и на классический
радиус электрона:
очень большая, чтобы ее можно было бы
отнести к собственному вращению частицы, поэтому хитрые ортодоксы и назвали ее
«спин». Момент импульса вращающегося вокруг собственной оси электрона
(собственный момент импульса) найдем, аналогично (2.2.2), умножив массу
электрона на его скорость вращения (равную скорости света) и на классический
радиус электрона:
![]() (2.2.3),
(2.2.3),
где ![]() - постоянная тонкой структуры. Поэтому собственный момент
импульса электрона в 137 раз меньше момента импульса на его винтовой
траектории.
- постоянная тонкой структуры. Поэтому собственный момент
импульса электрона в 137 раз меньше момента импульса на его винтовой
траектории.
3. Теперь
подсчитаем момент импульса электрона на орбите Бора, умножив его массу на
радиус орбиты и на скорость орбитального движения (в 137 раз меньше скорости света).
Мы опять получим значение ![]() , что и следовало ожидать по требованиям закона сохранения момента количества движения. Таким
образом, момент импульса электрона при захвате на орбиту атома остается таким
же самым, как был на винтовой траектории.
, что и следовало ожидать по требованиям закона сохранения момента количества движения. Таким
образом, момент импульса электрона при захвате на орбиту атома остается таким
же самым, как был на винтовой траектории.
4. Во многих местах монографии ясно показано, что винтовое движение частиц описывает все специфические волновые их свойства, хотя ни с какой настоящей волной они не связаны.
5. При внимательном анализе всех случаев экспериментально найденного корпускулярно-волнового дуализма микрочастиц это свойство оказывается прямым следствием их винтового движения.
6. Винтовое движение частиц правильно описывает и такие чисто волновые свойства, как интерференция, дифракция и поляризация, которые непонятны с точки зрения прямолинейного и равномерного движения, принятого в современной науке.
7. Результаты двухщелевого опыта Юнга вполне предсказуемы, если расстояние между щелями не превышает диаметра винтового движения. Если расстояние будет больше, то дифракционная картина даже отдельных электронов исчезнет. Аналогично, если диаметр отверстия будет меньше диаметра винтовой траектории, то частица уже не может проникнуть в это отверстие.
8. При захвате электрона на атомную орбиту или космического тела на орбиту планеты или спутника произведение скорости движения тела на радиус винтового движения в свободном состоянии полностью и однозначно определяет положение единственной орбиты этого тела после захвата. При равномерном и прямолинейном движении тел («инерциальные системы отсчета») параметры орбиты после захвата определяются прицельным расстоянием и скоростью движения, обе эти величины произвольны, поэтому образование атомов и планетных систем невозможно. Этот аргумент полностью отвергает первый закон Ньютона, квантовую механику и теорию относительности. Наука докатилась до такого состояния, что теоретиков стало гораздо больше, чем физических явлений. Поэтому каждое физическое явление нашло множество объяснений от правдоподобных до совершенно абсурдных. Например, при двухщелевом опыте некоторые «теоретики» считают, что в это момент Вселенная раздваивается. Очевидно, что для первого закона Ньютона, квантовой механике и теории относительности можно насобирать множество экспериментальных подтверждений, но они не доказывают правильности, а лишь одно явное противоречие способно доказать ошибочность любой теории. Жду от читателей подобного аргумента против новой физики.
9. Формула для сечения рассеяния, полученная в главе 10.2 на основе винтового движения показывает сечение рассеяния в 4 раза больше, чем для прямолинейного и равномерного движения и совпадает с экспериментом.
10. Умножим обе части формулы (2.2.1) на частоту:
![]() (2.2.4),
(2.2.4),
откуда ![]() (2.2.5),
(2.2.5),
но при классическом равномерном и прямолинейном движении частицы должно было бы быть: E=mV2/2. Общая энергия вдвое превышает энергию поступательного движения частицы из-за такого же вклада в энергию тангенциального движения по витку винтовой траектории.
11. Экспериментально измеренное давление света (формула 23.11) подтверждает движение фотонов по винтовой траектории. В главе 23 показана абсурдность вывода правильной формулы давления света современной теорией.
12. В главе 3.4. дана теория туннельного эффекта на основе винтового движения частиц, которая адекватно отражает соответствующие эксперименты в отличие от официальных представлений.
13. Приведу цитату из главы 23.8:
«Здесь необходимо привести цитату из книги современного английского физика Г. Липсона «Великие эксперименты в физике», М., 1972, стр. 73: «Однако существует еще более простое явление, которое гипотеза Ньютона (о копускулярности света – В.К.) не может объяснить – одновременное отражение и преломление света поверхностью стекла. Ньютон выдвинул весьма туманную идею о легком отражении и легком преломлении: он предположил, что луч, состоящий из набора корпускул, может в определенное время быть в состоянии, когда он легко отражается, а затем – в состоянии, когда он легко преломляется, и т.д. С помощью явлений интерференции, которые мы позднее рассмотрим, Ньютон смог оценить расстояние между этими состояниями, которое оказалось равным 1/89000 дюйма для красного света. Это составляет 2,7×10-5 см – не так уж далеко от половины длины волны красного света, как мы теперь знаем». Сейчас снова посмотрите на фигуру 23.8.1, чтобы оценить гениальную интуицию Ньютона, который фактически доказал не только корпускулярность света, но и движение его корпускул по винтовой линии. Жаль, что эта догадка затерялась в истории науки и осталась невостребованной ни самим Ньютоном, ни другими учеными. Иначе мы бы сейчас имели совсем другую науку».
Таким образом, убедительные доказательства винтового движения тел давно существуют, но ортодоксы их не замечают, иначе рушится вся современная физика.
2.3. Волновое, формально-математическое и корпускулярное описание мира
В науке общеизвестен факт, что часто прямо противоположные представления о том или ином явлении приводят к одинаковым конечным результатам, что вызывает ожесточенные дискуссии оппонентов. Примером может служить вековой спор между сторонниками волновой и корпускулярной природы света, спор между системой Птолемея и Коперника и многие другие конфликты в самых разных областях науки.
Волновое описание физических явлений невозможно осуществить без упругой среды (эфира) в которой возникает волновой процесс и распространяется посредством этой упругой среды. Поэтому описание волновых явлений в твердом теле, жидкости и газе адекватно отражает опытные данные и вопросов здесь не возникает. Там, где упругая среда отсутствует, приходится придумывать разные хитрости, чтобы распространить волновое описание и на эти объекты: пустое мировое пространство (мировой эфир в разных фантастических формах), внутреннее пространство атомов (волновые функции вероятности), поля (близкодействие полей посредством передачи возмущения от одной точки к другой), электромагнитное излучение Максвелла (одновременное колебание магнитного и электрического поля в упругой среде). Волновое описание мира прекрасно разработано, т.к. над ним трудились многие поколения известных ученых, но главным тормозом здесь остается необходимость иметь в наличии упругую среду. Там, где ее нет или возникают сомнения в ее существовании, там открывается поле для критики.
В формально-математическом описании мира упругая среда уже не нужна. Записывают волновое уравнение и решают его для самых разнообразных случаев. Хотя в математическом отношении такое описание мира безупречно, но физический смысл математических манипуляций теряется. Особенно это заметно в квантовой механике. Как следствие, подобное описание легко подвергнуть жестокой критике. Чтобы спастись от назойливых критиков, приходится придумывать совершенно фантастические представления о микромире, которым нет соответствия в макромире. Таким образом, единство мира нарушается, что прямо противоречит основным законам мироздания. Отсутствие физического смысла является главным неустранимым тормозом формально-математического описания мира.
Корпускулярное описание мира, в основном, является заслугой Ньютона. Из-за малочисленности сторонников такого описания «победили» волновые представления. Главный тормоз для корпускулярного мира установил сам Ньютон, сформулировав закон равномерного и прямолинейного движения свободных тел. Этот закон стал непреодолимым препятствием для объяснения интерференции, поляризации и некоторых других свойств света. Попытки совместить волновое описание с корпускулярным (корпускулярно-волновой дуализм микрочастиц) изначально обречены на провал из-за принципиальной разницы между волной и частицей. Для корпускулярного описания мира эфир не нужен ни в какой форме, поэтому фотон, например, может двигаться в пространстве миллиарды лет не «размазываясь», что невозможно с точки зрения волнового описания его движения. Главный недостаток корпускулярного описания мира состоит в неполноте официального инструментария для такого описания. Только новая корпускулярная квантовая физика ввела представление о возникновении гравидинамического поля при движении гравитационных зарядов и связанным с этим фактом винтовым движением свободных тел. Это позволило пересмотреть многие фундаментальные положения классической физики и квантовой механики и реализовать возможность корпускулярного описания мира в полной мере. К сожалению, это произошло после того, как в головах ученых прочно закрепилась парадигма, разработанная Эйнштейном и отцами квантовой механики. Эту парадигму успели вдолбить в головы миллионов студентов и даже домохозяек. В результате новая научная парадигма на основе новой физики встречает агрессивное неприятие. Это, конечно, временное явление и победа новой парадигмы в науке неизбежна, как было уже неоднократно. Жаль, что этот временной промежуток, обычно, превышает временное существование человека на этом свете, а ортодоксы постоянно самовоспроизводятся консервативной наукой.
Наиболее корректное определение спина частиц дано в книге «Физика микромира» под редакцией Д.В. Ширкова, М., 1980.
«Объяснить это расхождение теории с опытом удалось с помощью предположения, сделанного Дж. Уленбеком и С. Гаудсмитом в 1925 году о том, что электрон обладает еще одной внутренней степенью свободы – спином. Согласно этому предположению, электрон и большинство других элементарных частиц наряду с орбитальным моментом импульса обладают еще собственным механическим моментом импульса. Этот собственный момент и называют спином. Наличие спина у микрочастицы означает, что в некоторых отношениях она подобна маленькому вращающемуся волчку. Однако эта аналогия чисто формальная, т.к. квантовые законы существенно изменяют свойства момента импульса. Собственный момент, согласно квантовой теории, может быть у точечной частицы».
Вокруг спина ортодоксальная наука нагородила множество абсурдных спекуляций, что видно из конца приведенной цитаты.
В главе 2
показано, что электрон фактически имеет два значения «спина», момент ипульса на
винтовой траектории или орбитальный момент в атоме равный ![]() (не
(не ![]() !) и
собственный момент импульса в 137 раз меньше орбитального (глава 2.2).
Орбитальный спин легко посчитать умножив скорость
электрона на орбите Бора на радиус этой орбиты и на массу электрона. По закону
сохранения момента импульса орбитальный спин сохранится и у свободного
электрона, удаленного из атома. Собственный спин электрона найдем, умножив
классический радиус электрона на скорость света и на массу электрона. Спин
свободных частиц за исключением нейтрино имеет одинаковое значение
!) и
собственный момент импульса в 137 раз меньше орбитального (глава 2.2).
Орбитальный спин легко посчитать умножив скорость
электрона на орбите Бора на радиус этой орбиты и на массу электрона. По закону
сохранения момента импульса орбитальный спин сохранится и у свободного
электрона, удаленного из атома. Собственный спин электрона найдем, умножив
классический радиус электрона на скорость света и на массу электрона. Спин
свободных частиц за исключением нейтрино имеет одинаковое значение ![]() . Это
прямое следствие формулы де Бройля:
. Это
прямое следствие формулы де Бройля:
![]() (1)
(1)
проверенной для многих частиц.
Собственный
спин частиц может быть любым. Например, электрон состоит из
двух нейтрино, поэтому момент импульса свободного нейтрино будет ![]() . В
разделе монографии «Элементарные частицы» показано, что частицы могут состоять
из многих компонентов, которые вращаются со скоростью света по круговой орбите
радиусом, близким классическому радиусу электрона, а масса этих частиц
пропорциональна сумме абсолютных значений моментов импульсов компонентов в
свободном состоянии. Например, у нейтрального пиона
. В
разделе монографии «Элементарные частицы» показано, что частицы могут состоять
из многих компонентов, которые вращаются со скоростью света по круговой орбите
радиусом, близким классическому радиусу электрона, а масса этих частиц
пропорциональна сумме абсолютных значений моментов импульсов компонентов в
свободном состоянии. Например, у нейтрального пиона ![]() , состоящего из
электрона и позитрона (глава 9.2) суммарное абсолютное значение собственного
момента импульса будет
, состоящего из
электрона и позитрона (глава 9.2) суммарное абсолютное значение собственного
момента импульса будет ![]() , т.е. масса пиона будет больше массы
электрона, примерно, в 274 раза. Значение собственного спина нейтрального пиона
проблематично. Если верить официальным утверждениям, что он
равен нулю (возможно, что ортодоксы здесь не ошибаются), то приходиться
признать, что при собственном вращении в одном направлении частиц, содержащих
равное количество материи и антиматерии, их моменты имульсов направлены в
противоположные стороны (электрон-позитрон в пионе или нейтрино-антинейтрино в
фотоне) и суммарный момент равен нулю, а вместе с ним равен нулю и суммарный
магнитный момент. Несмотря на то, что компоненты в отдельности обладают
механическим и магнитным моментом. Эти рассуждения в некоторой степени
оправдывают деление частиц на фермионы у которых наблюдается отталкивание на
малом расстоянии и бозоны между которыми
взаимодействие практически не наблюдается.
, т.е. масса пиона будет больше массы
электрона, примерно, в 274 раза. Значение собственного спина нейтрального пиона
проблематично. Если верить официальным утверждениям, что он
равен нулю (возможно, что ортодоксы здесь не ошибаются), то приходиться
признать, что при собственном вращении в одном направлении частиц, содержащих
равное количество материи и антиматерии, их моменты имульсов направлены в
противоположные стороны (электрон-позитрон в пионе или нейтрино-антинейтрино в
фотоне) и суммарный момент равен нулю, а вместе с ним равен нулю и суммарный
магнитный момент. Несмотря на то, что компоненты в отдельности обладают
механическим и магнитным моментом. Эти рассуждения в некоторой степени
оправдывают деление частиц на фермионы у которых наблюдается отталкивание на
малом расстоянии и бозоны между которыми
взаимодействие практически не наблюдается.
2.5. Сказка о виртуальных частицах
Великие сказочники сочиняют добрые сказки для детей и не скрывают, что сказка – это обман и выдумка. Ученые тоже сочиняют сказки и мифы, но выдают их за истину. Это тоже выдумка и обман. Имеется очень простой критерий по которому можно легко определить, понимают ли ученые то, о чем говорят или водят читателя за нос. Когда они понимают что-то, то ясно излагают проблему, которую поймете и Вы. Но Вы не найдете ясного объяснения, что такое спин, спутанное состояние, «темная» материя и энергия, обменное взаимодействие, слабое взаимодействие, как движется частица микромира, физический смысл запрета Паули и многое другое. Если правдивость утверждения невозможно проверить, то на этом поле чудес собирается особенно много мошенников, есть среди них и ученые.
Кто видел
виртуальные частицы? Никто не видел, они не наблюдаемы, по утверждению
ортодоксов. Очень удобная сущность (как бог), которой можно, ничем не рискуя,
объяснить любое явление. Соотношениями неопределенности Гейзенберга можно, с
грехом пополам, объяснить рождение виртуальной частицы, обладающей массой и,
следовательно, энергией из ничего. Вместе с Гейзенбергом закроем глаза на закон
сохранения энергии. Но откуда берется заряд у виртуального электрона,
противореча закону сохранения электрических зарядов? Для него соотношение
неопределенности не существует. В настоящее время технически возможно
определение промежутка времени ![]() t=10-23 сек. По соотношению неопределенности
t=10-23 сек. По соотношению неопределенности ![]() виртуальная
частица будет иметь энергию не менее 60 Мэв. Представляете, сколько она может
дров наломать в микромире, оставаясь не наблюдаемой. По ортодоксальным
представлениям отдельная виртуальная частица существует очень короткое время
так, что нарушения закона сохранения энергии как бы и нет
(?!). Но ортодоксы спекулируют и с «физическим вакуумом», который
буквально кишит виртуальными частицами. Выходит, что в среднем в каждый момент
времени во Вселенной существует бесконечное число виртуальных частиц, требующих
для своего существования бесконечно большую энергию, которая возникла из
ничего. Чтобы довести ситуацию до полного абсурда, легко себе представить, что
мы движемся в пространстве, проходя бесконечно малое расстояние за бесконечно
малый промежуток времени. В этом случае наша энергия станет бесконечно большой
и сказку о виртуальных частицах можно выбросить в мусорную корзину.
виртуальная
частица будет иметь энергию не менее 60 Мэв. Представляете, сколько она может
дров наломать в микромире, оставаясь не наблюдаемой. По ортодоксальным
представлениям отдельная виртуальная частица существует очень короткое время
так, что нарушения закона сохранения энергии как бы и нет
(?!). Но ортодоксы спекулируют и с «физическим вакуумом», который
буквально кишит виртуальными частицами. Выходит, что в среднем в каждый момент
времени во Вселенной существует бесконечное число виртуальных частиц, требующих
для своего существования бесконечно большую энергию, которая возникла из
ничего. Чтобы довести ситуацию до полного абсурда, легко себе представить, что
мы движемся в пространстве, проходя бесконечно малое расстояние за бесконечно
малый промежуток времени. В этом случае наша энергия станет бесконечно большой
и сказку о виртуальных частицах можно выбросить в мусорную корзину.
2.6. Корпускулярно-волновой дуализм ортодокса
Экспериментальное обнаружение корпускулярно-волнового дуализма в микромире поставило официальную науку в положение крайней растерянности. Невозможно противоположные свойства двух разных объектов (волна и частица) совместить в одном объекте. Чтобы не признаваться в научной импотенции, лучше всего, перевести состояние растерянности на читателя.
Как шаман, ортодокс начинает прыгать вокруг него, колотить в бубен квантовой механики и бормотать свои заклинания: «В качестве первичного принципа корпускулярно-волновой дуализм лежит в основе квантовой механики и квантовой теории поля… свет представляет собой электромагнитные волны… предположение Планка о дискретном характере излучения… представление о частицах света – фотонах… исходя из релятивистской кинематики, фотонам был приписан импульс… де Бройль отметил релятивистскую инвариантность соотношения, связывающего четырехмерный вектор энергии-импульса частицы с четырехмерным волновым вектором… это предположение послужило исходным пунктом построения квантовой механики в форме Шредингера…
 …
…
введено описание микрочастиц с помощью векторов состояния, подчиняющихся принципу суперпозиции и принята их вероятностная интерпретация, позволившая избежать формального логического противоречия с корпускулярными представлениями (нахождение частицы одновременно в нескольких различных состояниях)… в квантовой теории поля переходят от классических полей к квантовым… частицы выступают, как возбужденные состояния системы (поля)…вторичное квантование… важнейшим проявлением корпускулярно-волнового дуализма является возможность испускания и поглощения частиц в результате взаимодействия квантовых полей». (Физическая энциклопедия под редакцией А.М. Прохорова. М., 1988, том 2, стр. 464-465).
После такой атаки, читатель погружается в гипнотическое состояние и перестает что-нибудь соображать, цель достигнута!
Мы не можем идти по официальному пути и «находить решение противоречия путем отказа». Поэтому есть смысл рассмотреть две модели корпускулярно-волнового дуализма, которые хоть как-то отрезвят читателя. Одна модель отдает преимущество частицам, а другая – волнам.
Модель частицы.
В этой модели официальные представления исходят из того, что частица остается частицей (локальным объектом, двигающимся в пространстве). Но движение частицы соответствует волновым законам. Чтобы эта модель имела право на существование, необходимо вводить какие-то новые неизвестные взаимодействия, заставляющие частицу противодействовать первому закону Ньютона. Они науке, пока не ведомы.
Здесь уместно пояснить физический смысл корпускулярно-волнового дуализма, предлагаемый новой физикой, как движение любых свободных тел (в том числе и макротел) по винтовой траектории, причиной которой является возникновение гравидинамического поля при движении гравитационных зарядов (масс). Таким образом, представления новой физики не только уточняют официальную модель частицы, но и распространяют корпускулярно-волновой дуализм на все мироздание. К сожалению, идеи новой физики проникнут в мозги твердолобых ортодоксов через длительное время из-за тотального монополизма на истину, но это их проблемы.
Модель волны.
В этой модели официальные представления не рассматривают частицу, как локальный объект, а заменяют ее волновым пакетом, который представляет собой суперпозицию плоских монохроматических волн с близкими значениями частот и волновых векторов.

|
|
|
|
|
|
|
На фигуре 2.6.1 изображен волновой пакет, как его представляет официальная физика. Он имеет определенное положение в пространстве (как частица) и в то же время «расплывается» во время движения в дисперсионной среде, т.к. в ней скорость распространения волны зависит от ее частоты. Этому ортодоксы очень рады, т.к. можно спекулировать о вероятностном расположении пакета и «подтвердить» соотношение неопределенностей Гейзенберга.
В этой модели ортодоксальный шаман продолжает свою дикую пляску. Мы не будем повторять его бред, а остановимся на главных моментах.
Волны в обсуждаемом волновом пакете (которые могут быть любого происхождения) являются волнами де Бройля. По официальному определению это волны, связанные с любой движущейся микрочастицей, отражающие квантовую природу микрочастиц. (Там же, том 1, стр. 330). Вы удовлетворены таким объяснением? Я – нет. Поэтому предлагаю посмотреть на «волновой пакет» другими глазами. Представим себе, что это просто группа фотонов с близкими частотами (параметрами винтовой траектории). Тогда все свойства этой группы, вплоть до, так называемой, фазовой скорости будут полностью соответствовать свойствам официального волнового пакета. Естественно, что группа фотонов будет «расплываться» в дисперсионной среде из-за разной скорости их движения. Размазывание одной частицы, несущей волновой пакет, противоречит закону сохранения энергии, т.к. энергия связи компонентов частиц имеет огромную величину.
Надеюсь, что теперь читатель освободился от состояния растерянности и покинул компанию ортодоксов.
В случае
взаимодействия «неподвижных» протона и электрона с формированием атома
водорода, электрон находит протон, имея энергию меньше 13,6 эв. Если энергия
электрона превышает это значение, то водородоподобный атом не возникает, т.к.
энергия электрона превышает энергию ионизации. Природу
здесь не обманешь. Однако, это не совсем верно и здесь
открывается новое поле для исследований. Можно заставить электрон и протон
создать атом водорода при любой скорости (энергии) электрона, пользуясь
современной техникой ускорения частиц. Для этого двигающийся в определенном
направлении электрон должен «догнать» протон, двигающийся в том же направлении.
При этом относительная скорость электрона не должна приводить к ионизации
возникающего атома водорода, т.е. желательно, чтобы они двигались в этот момент
с одинаковой скоростью. В этом случае электрон на своей винтовой траектории будет
вращаться вокруг протона, аналогично спутнику вокруг центрального тела и мы
можем воспользоваться расчетами главы 21.3. Параметрами винтовой траектории
протона пренебрежем, т.к. они почти в 2000 раз меньше в сравнении с электроном.
Масса электрона не меняется до тех пор, пока его тангенциальная скорость не достигнет скорости света, а радиус винтовой
траектории не станет равным 386 фм (глава 5.2.2). Поэтому, до этого момента
формулы главы 2 будут верны. Возникший атом водорода будет продолжать движение
со скоростью протона, а плоскость орбиты электрона будет перпендикулярна этому
движению. При включении в рассмотрение электростатического взаимодействия
электрона и протона ситуация будет полностью аналогична переходу спутника с
более высокой орбиты r1
на более низкую r2 с соответствующим увеличением скорости движения
на низкой орбите, но с непременным сохранением момента импульса электрона,
равным ![]() .
Поэтому для не релятивистского случая можно записать:
.
Поэтому для не релятивистского случая можно записать:
![]() (2.7.1),
(2.7.1),
но
![]() (2.7.2),
(2.7.2),
где V1 – поступательная скорость протона и электрона, r1 – радиус высокой орбиты (радиус винтовой траектории электрона перед захватом), а m0 – масса покоя электрона.
В дальнейшем нас будет интересовать зависимость r2 и энергии связи электрона с протоном от скорости поступательного движения атома водорода или от энергии догоняющего электрона. Потенциальная энергия электростатического притяжения электрона и протона:
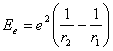 (2.7.3).
(2.7.3).
По теореме вириала и в соответствии с расчетами главы 21.3 половина этой энергии пойдет на увеличение потенциальной энергии универсального отталкивания, а вторая половина на энергию связи. Поэтому энергия связи численно равна:
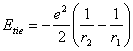 (2.7.4).
(2.7.4).
Увеличение потенциальной энергии универсального отталкивания равно:
![]() (2.7.5).
(2.7.5).
Поскольку
момент импульса электрона всегда один и тот же ![]() :
:
![]() , а
, а ![]() (2.7.6).
(2.7.6).
Подставив (2.7.6) в (2.7.5) и приравняв полученное выражение (2.7.4), после некоторых преобразований получим:
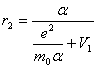 (2.7.7),
(2.7.7),
где ![]() =
1,1556 см2/сек для электрона (глава 2).
=
1,1556 см2/сек для электрона (глава 2).
При V1 ®0 формула (2.7.7) совпадает с формулой (2.3) главы 2:
![]() (2.7.8).
(2.7.8).
Для водородоподобных атомов в знаменатель (2.7.8) надо подставить заряд ядра Z.
Радиус винтовой траектории свободного электрона:
![]() (2.7.9).
(2.7.9).
Подставив (2.7.9) и (2.7.7) в (2.7.4) после преобразований получим формулу для энергии связи электрона с протоном, совпадающую с формулой (2.4) главы 2:
![]() (2.7.10).
(2.7.10).
Для водородоподобных атомов в числитель (2.7.10) надо подставить Z 2.
Удивительно, что энергия связи электрона с ядром не зависит от скорости движения ядра (если эта скорость не релятивистская и изменением массы электрона можно пренебречь). Поэтому атомы, двигающиеся с большой скоростью не изменяют спектр излучения, только за счет эффекта Доплера он смещается в целом в ту или другую сторону. Вместе с тем, размеры атомов сокращаются в направлении поперек их движения в соответствии с формулой (2.7.7). Это утверждение новой физики обратно утверждению теории относительности. График изменения размера атома водорода в зависимости от скорости его движения представлен на фигуре 2.7.1. Он построен по расчетной формуле:
![]() (2.7.11)
(2.7.11)
|
|
|
|
|
|
в координатах: скорость (в долях от скорости света) – радиус (в долях от
радиуса орбиты Бора).
2.8 Винтовая траектория релятивистского электрона
Момент импульса не релятивистского электрона:
![]() (2.8.1),
(2.8.1),
где m0 – масса покоя частицы.
Релятивистский электрон увеличивает свою массу от скорости движения:
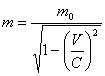 (2.8.2).
(2.8.2).
Формула (2.8.2) хотя и не совсем точна (см. главу 5.2 и фигуру 5.2.1), но, приблизительно правильно описывает изменение массы частицы во всем диапазоне возможных скоростей. Подставим (2.8.2) в (2.8.1):
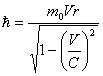 (2.8.3).
(2.8.3).
Если в
(2.8.1) Vr =![]() = 1,1576 см2/сек,
то в (2.8.3) произведение Vr не остается постоянным с увеличением массы
частицы, постоянным остается только момент импульса по требованию закона
сохранения его, поэтому Vr уменьшается. Поступательная скорость частицы V
– аргумент, поэтому уменьшение этого произведения происходит за счет уменьшения
радиуса винтовой траектории частицы, что обусловлено усилением
гравидинамического поля с ростом движущейся массы. Из (2.8.3):
= 1,1576 см2/сек,
то в (2.8.3) произведение Vr не остается постоянным с увеличением массы
частицы, постоянным остается только момент импульса по требованию закона
сохранения его, поэтому Vr уменьшается. Поступательная скорость частицы V
– аргумент, поэтому уменьшение этого произведения происходит за счет уменьшения
радиуса винтовой траектории частицы, что обусловлено усилением
гравидинамического поля с ростом движущейся массы. Из (2.8.3):
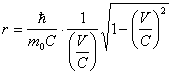 (2.8.4).
(2.8.4).
В формуле
(2.8.4) ![]() - величина постоянная, обозначим ее K.
На фигуре 2.8.1 Приведены графики изменения величины r/K для не релятивистской частицы
(кривая 1) и для релятивистской частицы по формуле (2.8.4) (кривая 2) в
зависимости от отношения V/C, где С –
скорость света. Из фигуры видно, что траектория релятивистской частицы
отличается от медленной при V/C >0,2.
- величина постоянная, обозначим ее K.
На фигуре 2.8.1 Приведены графики изменения величины r/K для не релятивистской частицы
(кривая 1) и для релятивистской частицы по формуле (2.8.4) (кривая 2) в
зависимости от отношения V/C, где С –
скорость света. Из фигуры видно, что траектория релятивистской частицы
отличается от медленной при V/C >0,2.
|
|
|
|
|
|
2.9. Релятивистские атомы водорода
В главах 2.7. и 2.8. обсуждены проблемы создания атомов водорода при взаимодействии быстро движущихся электрона и протона. Здесь будем рассматривать винтовую траекторию релятивистского электрона, параметры винтовой траектории протона в 2000 раз меньше, поэтому будем условно считать его движение прямолинейным. Очевидно, что винтовая траектория создается собственным гравидинамическим взаимодействием частицы, пропорциональным массе частицы и ее скорости поступательного движения. Поскольку гравидинамическое взаимодействие самое сильное в природе, то при некоторой скорости электростатическим взаимодействием протона с электроном можно пренебречь. Это касается скоростей выше «тепловых». Сначала найдем, как меняется фиктивная масса «протона» Mf, чтобы обеспечить данный радиус винтовой траектории, если учитывать только гравитационное взаимодействие этой массы с электроном. Массовый эквивалент электростатического и гравидинамического взаимодействия найден в главе 11.2.5. Затем, зная изменение Mf от скорости, найдем соответствующее изменение фиктивного заряда «протона» Zf .
Устойчивое орбитальное движение космического тела реализуется только в том случае, если его орбитальная скорость V определяется из равенства силы притяжения к центральному телу массой Mf и центробежной силы:
![]() (2.9.1),
(2.9.1),
|
|
|
|
|
|
где G –
гравитационная постоянная (6,6726×10-8
дн×см2/г2),
r – радиус винтовой траектории электрона. В главе 2.8. он
найден:
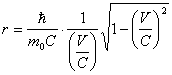 (2.9.2).
(2.9.2).
Подставив (2.9.2) в (2.9.1), после некоторых преобразований, найдем, как Mf изменяется в зависимости от значения V/C :
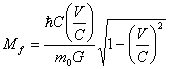 (2.9.3).
(2.9.3).
Значение
константы ![]() = 0,52×1018
г.
= 0,52×1018
г.
График изменения Mf от V/C показан на фигуре 2.9.1 в координатах: V/C – Mf /1017 г.
График изменения Zf показан на фигуре 2.9.2 в координатах V/C – Zf /1023.
|
|
|
|
|
|
В соответствии с главой 11.2.5 массовый эквивалент единицы электрического
заряда 1,859×10-6 г. При
этом они взаимодействуют одинаково. Разделив фиктивную массу на 1,859×10-6 г, найдем фиктивный
электрический заряд, который мог бы обеспечивать такой же радиус винтовой
траектории релятивистского электрона. Мы получили настолько большие значения
фиктивного заряда и фиктивной массы, что об электростатическом взаимодействии и
тем более о гравитационном взаимодействии в сравнении с гравидинамическим
взаимодействием при таких скоростях движения можно забыть.
Обратите внимание на ход кривой от V/C =0,707 (максимум кривых) до V/C = 0,866. Смотри главу 5.2, фигуру 5.2.1. Этот диапазон скоростей как раз приходится на переходную область, когда тангенциальная скорость электрона на винтовой траектории достигает скорости света и не может больше увеличиваться. Поэтому собственное гравидинамическое поле электрона больше не растет, но зато резко увеличивается его масса за счет продолжающегося увеличения поступательной скорости, поэтому центробежная сила, пропорциональная квадрату скорости, превышает гравидинамическую силу, пропорциональную скорости в первой степени. В результате при дальнейшем увеличении поступательной скорости Mf и Zf уменьшаются. При поступательной скорости частицы, равной скорости света, ее масса стала бы бесконечно большой, что приводит к нулевым значениям Mf и Zf .
Релятивистские
атомы водорода обладают большой проникающей способностью подобно нейтронам, но
в отличие от последних стабильны. Переход электрона на
разные энергетические уровни у них невозможен, поэтому излучение отсутствует.
Ионизировать релятивистский атом водорода можно только при относительном
движении протона и электрона вдоль оси винтовой траектории. Электростатическая
энергия связи в этом случае равна ![]() , где r определено формулой (2.9.2).
, где r определено формулой (2.9.2).
Экспериментаторы, подтвердившие изложенную теорию, вполне могут рассчитывать на крупное научное достижение.