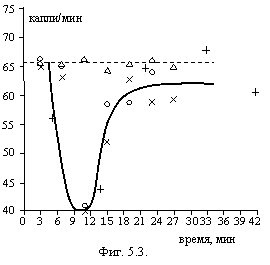КОЛЛОИДНЫЕ СИСТЕМЫ

1 Кинетическое уравнение коагуляции

Частицы коллоидов и суспензий по отношению к молекулам являются макрообъектами, а в сравнении с обычными макрообъектами имеют микроскопические размеры, т.е. занимают промежуточное положение в масштабной иерархии. Поэтому продолжим наш путь от элементарных частиц ко Вселенной в целом

 Вместе с тем они имеют свои специфические свойства, использование которых важно для биологии и технологии. Все живые организмы фактически представляют собой коллоидные системы.

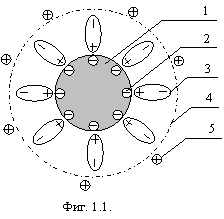
Напомню, как устроена коллоидная частица (или более крупная частица суспензии), показанная на фигуре 1.1.

На фигуре 1.1: 1 – коллоидная частица, 2 – потенциалопределяющие ионы, адсорбированные на поверхности частицы, 3 – сольватный слой ориентированных диполей (молекул воды) толщиной до нескольких сотен молекул, 4 – поверхность скольжения в дисперсионной среде, 5 – противоионы.

При броуновском движении частицы, если противоионов мало, то они не успевают скомпенсировать электрический заряд потенциалопределяющих ионов, поэтому частица обладает некоторым электрическим потенциалом  (дзета-потенциал). Дзета-потенциал обусловливает устойчивость к слипанию (коагуляции) коллоидных частиц. Если в дисперсионной среде окажется достаточное количество противоионов, -потенциал снижается и происходит коагуляция. Коллоидные частицы слипаются между собой, но электрический заряд их при этом практически не меняется, из-за чего они не могут образовать крупный единый агрегат. Поэтому в кинетическом уравнении Смолуховского необходимо учитывать равновесную счетную концентрацию агрегатов . Значение  связано, с одной стороны, с электростатическим отталкиванием частиц, составляющих агрегат, с другой стороны, эта величина зависит от прочности сцепления частиц в агрегате, которая зависит от состояния сольватного слоя.

Принимая, по Смолуховскому, второй порядок для кинетики слипания частиц с учетом равновесной счетной концентрации, можно записать:

                                        (1.1.),

где C – текущая концентрация частиц, 1/см³.

Решение уравнения (1.1.) можно представить в следующем виде:

                                  (1.2.),

где C₀ – начальная счетная концентрация частиц, 1/см³, K – константа скорости коагуляции, см³/сек.

Кинетическое уравнение Смолуховского:

                                          (1.3.)

является частным случаем уравнения (1.2.) при =0. Уравнение Смолуховского показывает достаточно хорошее согласие с экспериментом только в начальном периоде коагуляции. В дальнейшем убыль концентрации частиц идет медленнее, чем по уравнению (1.3.).

При пользовании уравнением (1.2.) возникает вопрос определения равновесной концентрации агрегатов. Для глубоких стадий процесса C приближается к  и точность обработки экспериментальной кривой сильно зависит от ошибки определения . Если концентрацию C₀ принять за единицу, тогда C и  будут выражены в долях единицы и равновесную концентрацию можно определить из координат двух экспериментальных точек (₁, C₁) и (₂, C₂) по уравнению:

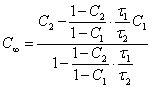                                    (1.4.),

которое получено из (1.2.). Умножением найденного значения  на C₀ и подстановкой в (1.2.) получим значение константы скорости коагуляции. Если уравнение (1.2.) преобразовать к виду:

                                  (1.5.),

то более точное значение константы скорости можно найти из тангенса угла наклона прямой в координатах:  - время.

Было бы неверно искать энергию активации процесса коагуляции по зависимости найденной константы скорости от температуры процесса, т.к. в этом случае не учитывается уменьшение вязкости раствора с повышением температуры, что приведет к получению значения энергии активации выше действительного.

По Смолуховскому, константа скорости коагуляции определяется выражением:

                                        (1.6.),

где: k – константа Больцмана, эрг/град,

T – абсолютная температура, град,

 - вязкость коллоидного раствора, дин×сек/см²,

W – вероятность эффективного столкновения частиц.

Здесь следует отметить, что при быстрой коагуляции величина W может оказаться больше единицы за счет притяжения коллоидных частиц, несмотря на то, что они одноименно заряжены. Это притяжение обусловлено взаимной перестройкой внешних сольватных слоев сближающихся частиц.

Определив экспериментальное значение константы скорости, из (1.6.) можно найти W. По зависимости W от температуры процесса найдем энергию активации коагуляции из уравнения:

                                 (1.7.),

где E – энергия активации, эрг/г-моль..

Расчет по (1.7.) автоматически учитывает изменение вязкости коллоидного раствора с температурой и поэтому позволяет найти более точное значение энергии активации процесса. Здесь следует уточнить, что энергия активации коагуляции имеет отношение только к прочности рыхлой наружной части сольватного слоя коллоидных частиц. Внутренние части сольватного слоя настолько прочны, что их перестройка и постепенное уплотнение агрегатов может происходить в течение нескольких лет. Из этого факта можно сделать вывод, что энергия активации перестройки сольватного слоя резко увеличивается по мере углубления в него, что указывает на его особую прочность вблизи поверхности коллоидной частицы.

Непосредственная экспериментальная проверка кинетического уравнения (1.2.) возможна с помощью поточного ультрамикроскопа. Я обработал большое число литературных данных по кинетике коагуляции. Если отклонение от уравнения Смолуховского в случае медленной коагуляции не вызывает сомнений, то для быстрой коагуляции это уравнение, обычно считают справедливым, хотя кинетика изучалась только в начале процесса. Однако, следует отметить, что даже в случае «сверхбыстрой» коагуляции, когда W>1 и коллоидные частицы притягиваются друг к другу, они все-таки обладают -потенциалом отличным от нуля. Это приводит к тому, что по мере накопления частиц в агрегате электростатический барьер увеличивается для прилипания последующих частиц. Кроме того, из-за броуновского движения или градиента скоростей дисперсионной среды рыхлые крупные агрегаты разрушаются. 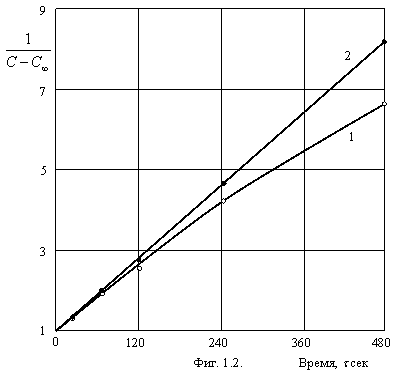Таким образом, и в этом случае мы будем иметь хотя и малое, но вполне измеримое значение . 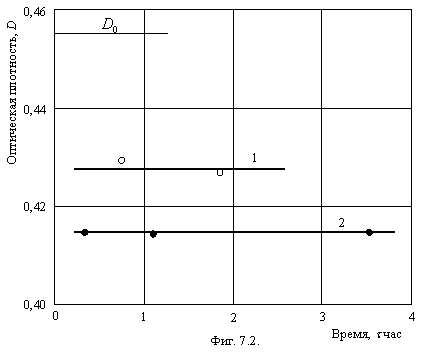Для примера, на фигуре 1.2. приведены результаты расчета быстрой коагуляции золя золота по данным (Г.Р. Кройт. Наука о коллоидах. ИЛ, М., 1955). , найденное из (1.4.) равно 0,028×C₀. Кривая 1 – по уравнению Смолуховского, прямая 2 – по предлагаемому уравнению (1.2.).

Из фигуры 1.2. видно, что кинетическое уравнение Смолуховского не подходит для данной системы, т.к. не получается прямой линии при =0. В то же время, уравнение (1.2.) хорошо описывает рассматриваемый случай коагуляции, приводящийся в литературе в подтверждение правильности уравнения Смолуховского. Константа скорости, найденная из угла наклона полученной прямой оказалась равной 7,38×10^-12 см³/сек. Это значение, по-видимому, несколько завышено, т.к. перемешивание коллоидного раствора при применении поточного ультрамикроскопа неизбежно. В следующей главе будет предложен метод исследования кинетики коагуляции свободный от этого и других недостатков. Вероятность эффективного столкновения частиц из (1.6.) равна 1,38, что указывает на быструю коагуляцию.

Таким образом, уточнение уравнения Смолуховского, проведенное нами выше, позволяет значительно расширить область его применения.

2 Оптический метод изучения кинетики коагуляции

Предлагаемый ниже оптический метод изучения кинетики коагуляции будет полезен особенно медицине, т.к. обладает исключительной простотой, точностью и чувствительностью. Он позволит с высокой чувствительностью по кинетике коагуляции элементов крови определять патологию, яды и другие вещества в организме.

Метод изучения кинетики коагуляции посредством поточной ультрамикроскопии не может быть широко внедрен в лабораторную практику по двум обстоятельствам. Первое заключается во влиянии перемешивания коллоидного раствора, неизбежного в поточной ультрамикроскопии, на кинетику процесса. Вторая трудность связана со сложностью соответствующего оборудования и трудоемкостью эксперимента. Эти обстоятельства вынудили меня полученное в предыдущей главе уравнение модифицировать таким образом, чтобы его можно было применить к экспериментальным данным изменения оптических свойств коллоидных систем, полученным на фотоколориметре. Запись изменения оптической плотности коллоидной системы производится самописцем. Чтобы избежать перемешивания раствора и избежать влияния седиментации агрегатов, процесс ведут в герметично закрывающейся термостатированной кювете без пузырьков воздуха в ней. Кювета медленно (2 об/мин) вращается, при этом образующиеся в коллоидной системе агрегаты за счет седиментации описывают окружности очень малого диаметра в сравнении с диаметром светового луча, считывающего оптическую плотность. Таким образом, эксперименты по коагуляции полностью автоматизированы и на них не влияют посторонние воздействия.

2.1. Крупные коллоидные частицы (суспензии).

Если размер коллоидных частиц больше 1/3 длины волны светового излучения (суспензии), по теории Ми, частица в агрегате проявляет свою индивидуальность и выступает как единичный рассеивающий центр. Если размер частицы меньше 1/4 длины волны светового излучения (коллоиды) индивидуальность отдельной частицы теряется и, как единичный рассеивающий центр, выступает уже агрегат. Для таких частиц справедлива теория Рэлея.

Представляет интерес рассмотрение трех случаев: коагуляция в цепочки, плоскости и объемные агрегаты, т.к. все эти виды структур могут быть получены как на модельной, так и на технологических системах.

Для случая агрегирования в цепочки, текущая оптическая плотность будет пропорциональна 2N+1, где N – число частиц в агрегате, т.к. из условия равновероятного положения агрегатов, прибор будет «видеть» из каждых трех агрегатов, два агрегата с числом частиц N и один агрегат с числом частиц равным единице (с «торца»). Начальная оптическая плотность пропорциональна общему количеству частиц в этих трех агрегатах, равному 3N. Таким образом, из отношения начальной оптической плотности к текущей, найдем для линейных агрегатов:

                                     (2.1.1.).

Аналогично рассуждая, найдем для плоских и объемных агрегатов, соответственно:

                                    (2.1.2.),

                                           (2.1.3.).

С другой стороны, очевидно, что число частиц в агрегате в любом случае:

                                           (2.1.4.),

где: C₀ – начальная счетная концентрация частиц, 1/см³,

C – текущая счетная концентрация частиц, 1/см³.

Подставив (2.1.4.) в (2.1.1.), (2.1.2.) и (2.1.3.), получим связь между счетной концентрацией частиц и оптической плотностью суспензии при образовании линейных, плоских и объемных агрегатов соответственно:

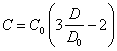                                     (2.1.5.),

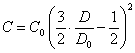                                 (2.1.6.),

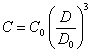                                     (2.1.7.).

Вид уравнений (2.1.5.), (2.1.6.) и (2.1.7.), как видно из предыдущего, не зависит от плотности упаковки частиц в агрегатах. Из них также видно, что процесс коагуляции в рассматриваемом случае крупных коллоидных частиц (суспензий) приводит к уменьшению оптической плотности суспензии.

Подставляя полученные уравнения в (1.2.) предыдущей главы, после некоторых преобразований, найдем для линейных агрегатов:

                          (2.1.8.),

для плоских агрегатов:

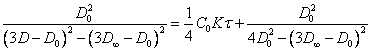       (2.1.9.)

и для объемных агрегатов:

                           (2.1.10.).

Уравнения (2.1.8.), (2.1.9.) и (2.1.10.) дают прямые линии в координатах, по оси ординат которых отложены значения левой части уравнений, а по оси абсцисс – время.

Величина  может быть найдена из координат любых трех экспериментальных точек (₁, D₁), (₂, D₂), (₃, D₃) по уравнению:

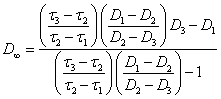                      (2.1.11.)

для линейных агрегатов. Для объемных агрегатов:

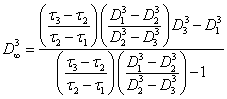                    (2.1.12.).

Уравнения (2.1.11.) и (2.1.12.) хотя и громоздки, но удобны для практических расчетов. Выражение для D_¥ в случае плоских агрегатов более сложно:

              (2.1.13.),

где:

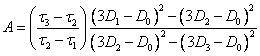              (2.1.14.).

Для равноотстоящих значений  уравнения (2.1.11.), (2.1.12.) и (2.1.13.) значительно упрощаются.

Таким образом, используя уравнения (2.1.8.), (2.1.9.) и (2.1.10.) вместе с выражениями (2.1.11.), (2.1.12.) и (2.1.13.) для  легко найти из измерений оптической плотности константу скорости коагуляции суспензии и, следовательно, эффективность столкновения частиц.

2.2. Коллоидные системы из мелких частиц.

Малые частицы, собранные в агрегат, не проявляют оптически своей индивидуальности и агрегат в целом выступает как один рассеивающий центр. Это положение справедливо для частиц меньших 1/4 длины волны светового излучения, т.е. расположенных левее максимума рассеяния по теории Ми.

По Рэлею (Г.Р. Кройт. Наука о коллоидах. ИЛ, М., 1955, стр. 413) оптическая плотность коллоида пропорциональна квадрату объема рассеивающей свет частицы:

                                           (2.2.1.),

где: k – коэффициент пропорциональности, 1/см³,

C – концентрация частиц в единице объема, 1/см³.

Записывая отношение текущей оптической плотности к начальной, получим:

                                          (2.2.2.).

Вес агрегата, образовавшегося к моменту времени t:

                                   (2.2.3.),

где: r₀ – радиус частицы, см,

r – радиус агрегата, см,

N – число частиц в агрегате,

 - плотность частицы, г/см³,

¢ - плотность агрегата, г/см³.

Из (2.2.3.), учитывая, что N=C₀/C и обозначая ¢ /=, где - плотность упаковки, в пределе, изменяющаяся от 0 до 1, найдем:

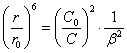                                   (2.2.4.)

Подставив (2.2.4.) в (2.2.2.), получим:

                                     (2.2.5.).

Из уравнения (2.2.5.) видно, что в отличие от крупных частиц суспензий, коагуляция мелких частиц коллоидов приводит к увеличению оптической плотности золя.

Подставив (2.2.5.) в (1.2.), получим уравнение кинетики коагуляции золя, выраженное через оптическую плотность:

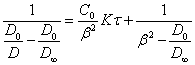                         (2.2.6.).

Уравнение (2.2.6.) дает прямую линию в координатах: 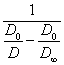 - время, откуда может быть найдена константа скорости коагуляции. Величина  вносит некоторую неопределенность в истинное значение константы скорости.

Значение  может быть найдено по координатам трех экспериментальных точек (₁, D₁), (₂, D₂) и (₃, D₃) из уравнения:

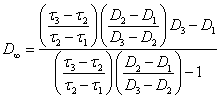                       (2.2.7.).

Таким образом, пользуясь результатами главы 2.1. и 2.2. возможно изучение коагуляции суспензий и золей во всем диапазоне размеров частиц, соответствующим подбором длины волны света, при которой проводят измерения оптической плотности.

Наши эксперименты с коагуляцией суспензий (TiO₂) и золей (AgJ) показали, что равновесный размер агрегатов в зависимости от концентрации электролита при пороге коагуляции достигает максимальных размеров, а ход изменения  представляет собой практически точную дифференциальную кривую скорости коагуляции.

3. Связь между дзета-потенциалом и активностью ионов в двойном электрическом слое.

В литературе отсутствуют количественные оценки изменения свойств раствора, например значения pH вблизи коллоидных частиц. Вместе с тем этот показатель в основном определяет судьбу гидролиза растворов и адсорбцию примесей на продуктах гидролиза. В связи с этим возникает необходимость количественной оценки активности ионов электролитов вблизи коллоидных частиц.

Как показали наши опыты с гидролизом сернокислого титана, в зависимости от условий возможно получение метатитановой кислоты как в коагулированном состоянии, так и в виде золя с положительным -потенциалом. Высокая устойчивость такого золя к агрегированию не может быть объяснена теорией Дерягина-Ландау-Фервея-Овербека (ДЛФО)  отталкиванием частиц при перекрытии двойных диффузных электрических слоев кристаллитов метатитановой кислоты из-за высокой концентрации электролитов в маточном растворе. Более вероятной причиной устойчивости является наличие сольватного слоя, окружающего частицы метатитановой кислоты и при этом настолько прочного, что адсорбированные из раствора ионы располагаются на его поверхности и распределение ионов вокруг коллоидной частицы представляется тонким слоем на поверхности ее сольватного окружения.

Вывод основного уравнения, связывающего активность ионов на поверхности сольватного слоя с активностью их в маточном растворе и -потенциалом коллоидных частиц базируется на определении концентрационного потенциала (Н.А. Измайлов. Электрохимия растворов. М., 1966, стр. 467):

                                            (3.1.)

и обсуждении механизма адсорбции ионов с учетом принципа детального равновесия.

Для определенности, допустим, что коллоидная частица заряжена положительно и потенциалопределяющие ионы прочно хемосорбированы поверхностью частицы и не способны к обмену. Обозначим потенциал коллоидной частицы без противоионов через . Полагаем, что при адсорбции ионов потенциал такой частицы снижается на величину, определяемую концентрационным потенциалом данного сорта катионов и анионов. Допустим, что частица находится в воде, не содержащей электролитов. Тогда противоионами будут ионы гидроксила, и общее изменение потенциала частицы составит:

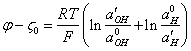                             (3.2.),

где: , и ,  - активности, соответственно, гидроксила и протона на поверхности сольватного слоя и в растворе, г-моль/л,

F – число Фарадея, к/г-моль,

- дзета-потенциал коллоидной частицы в отсутствие электролита, в.

Найдем связь между активностями катиона и аниона в равновесном диффузном двойном электрическом слое, тогда из принципа детального равновесия следует, что в таком же соотношении катионы и анионы будут сорбироваться и на поверхность сольватного слоя коллоидных частиц.

Из условия равновесия сил для данного катиона в диффузном двойном электрическом слое следует:

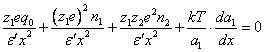                  (3.3.),

где: e – заряд электрона, ед. СГСЕ,

q₀ – заряд частицы без противоионов, ед. СГСЕ,

n₁, n₂ – число катионов и анионов в двойном электрическом слое внутри сферы, на поверхности которой находится данный катион,

¢ - диэлектрическая постоянная среды в двойном электрическом слое,

x – расстояние от центра частицы до данного катиона, см,

z₁ и z₂ – валентность, соответственно, катиона и аниона.

В уравнении (3.3.) члены последовательно соответствуют: силе притяжения катиона к частице, силе отталкивания от одноименных ионов, силе притяжения к ионам противоположного знака и «диффузной» силе, соответствующей отталкиванию от частицы.

Записывая аналогичное выражение для аниона и подставляя n₂ из него в (3.3.), получим дифференциальное уравнение, связывающее активности катиона и аниона в двойном электрическом слое. Решение этого уравнения следующее:

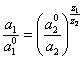                                         (3.4.).

Заряды катиона и аниона в уравнении (3.4.) взяты по абсолютной величине. Это уравнение будет справедливо и для плоского двойного электрического слоя, т.к. вид первых трех членов уравнения (3.3.) не влияет на решение.

Подставляя (3.4.) в (3.2.), получим:

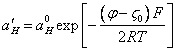                              (3.5.).

Потенциал  для большинства золей составляет около 0,2-0,3 в, а  около 0,1 в. Тогда из уравнения (3.5.) следует, что pH возле частицы очищенного отрицательно заряженного гидрозоля, приблизительно, на 2 единицы меньше, чем в растворе при pH~7.

Полученный результат полностью совпадает с экспериментальными данными (Harter Robert D., Anlrichs James L. Soil Sci. Soc. America Proc.,31, 30, #1, 1967), которые нашли, что на поверхности бентонитовой глины pH на 2 единицы меньше, чем в растворе при pH~7.

Для случая, когда в растворе присутствует электролит и  снижается до значения , аналогично (3.2.) можно записать:

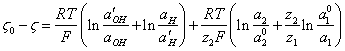        (3.6.),

где: , и ,  - активности, соответственно, гидроксила и аниона, протона и катиона на поверхности сольватного слоя, г-моль/л,  и  - активности, соответственно, аниона и катиона в растворе, г-моль/л.

Из (3.6.), используя (3.4.), найдем:

                             (3.7.).

Уравнение (3.7.) с учетом (3.5.) легко преобразовать к виду, удобному для подсчета pH возле положительно заряженных коллоидных частиц:

                          (3.8.),

где: pH₀ – значение pH в маточном растворе.

Для отрицательно заряженных коллоидных частиц знаки двух последних членов уравнения (3.8.) нужно изменить на противоположные.

Физический смысл полученного выражения состоит в зависимости адсорбции ионов водорода на поверхности сольватного слоя коллоидных частиц от наличия в растворе других ионов.

Подставляя (3.7.) в (3.6.), найдем активность противоионов на поверхности сольватного слоя для положительно или отрицательно заряженных коллоидных частиц:

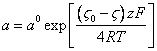                                   (3.9.),

где: z – валентность противоиона.

4. Адсорбция примесей на сольватном слое частиц и критерий устойчивости коллоидных систем.

Многочисленные эксперименты со всей очевидностью показывают, что агрегативная устойчивость коллоидных систем определяется наличием прочного сольватного слоя, окружающего коллоидные частицы. Все наши попытки объяснить опытные данные с позиций единственной в настоящее время количественной теории устойчивости коллоидов Дерягина-Ландау-Фервея-Овербека неизменно вступали в противоречие с экспериментом. В основу этой теории заложены два основных взаимодействия: ван-дер-ваальсово притяжение и отталкивание при перекрытии диффузных слоев противоионов коллоидных частиц. В технологических системах в отличие от модельных лабораторных систем отсутствуют оба фактора. Первый – из-за наличия толстого сольватного слоя, превышающего по размерам радиус действия ван-дер-ваальсовых сил, второй – из-за высокой концентрации электролитов.

В работе (Г.А. Мартынов, В.П. Смилга. Коллоидный журнал, 27, 250, 1965) было показано, что частицы, покрытые диполями будут притягиваться. Такой вывод основан на высокой подвижности полярных молекул на наружной границе сольватного слоя. Однако, по моему мнению, знак взаимодействия зависит от количества противоионов, адсорбированных на поверхности сольватного слоя. Если противоионов недостаточно, то диполи на поверхности сольватного слоя не успевают поворачиваться за время столкновения коллоидных частиц и между ними наблюдается отталкивание. Если противоионов достаточно для разрыхления наружной поверхности в такой степени, что диполи можно считать практически свободными, то отталкивание сменяется притяжением в соответствии с вышеуказанной ссылкой. Частицы в этом случае образуют агрегат в результате соприкосновения сольватных оболочек.

Ниже дан вывод уравнения, связывающего адсорбцию ионов на поверхности сольватного слоя коллоидных частиц с коэффициентом активности их в растворе. На основе этого уравнения получен критерий устойчивости коллоидных систем, устойчивость которых связана с наличием сольватного слоя.

Скорость адсорбции противоионов на поверхность сольватного слоя:

                                            (4.1.),

где: K₁ – константа скорости адсорбции, см²/сек,

₁ – поверхностная плотность противоионов в дисперсионной среде, 1/см².

Скорость десорбции противоионов с поверхности сольватного слоя в дисперсионную среду:

                                           (4.2.),

где: K₂ – константа скорости десорбции, см²/сек,

₂ – поверхностная плотность противоионов на сольватном слое, 1/см².

Поскольку факторы, затрудняющие установление равновесия в обсуждаемом случае отсутствуют, равновесие устанавливается достаточно быстро:

                                         (4.3.).

Подставляя в (4.3.) уравнение Аррениуса:

                                    (4.4.)

и очевидное соотношение между ₁ и концентрацией противоионов в объеме коллоидного раствора:

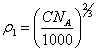                                        (4.5.),

найдем:

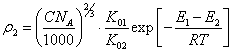                        (4.6.).

За энергию активации десорбции, в первом приближении, опуская взаимодействие с сольватным слоем, примем электростатическую энергию взаимодействия противоиона, находящегося на поверхности сольватного слоя, с заряженной коллоидной частицей:

                                    (4.7.),

где: q – заряд коллоидной частицы, ед. СГСЕ,

z – валентность противоиона,

 - расстояние от центра коллоидной частицы до наружной поверхности сольватного слоя, см,

¢ - средняя эффективная диэлектрическая постоянная сольватного слоя (она уменьшается по мере приближения к поверхности частицы).

Уравнение (4.7.) без ущерба для дальнейшего вывода можно заменить очевидным и более общим соотношением: E₂=E₂(₂).

Энергия активации адсорбции в рассматриваемом случае равна избыточной работе переноса противоиона из объема коллоидного раствора на поверхность сольватного слоя. Эта работа равна сумме избыточной работы по переносу противоиона из данного раствора в бесконечно разбавленный раствор (Н.А. Измайлов. Электрохимия растворов. М., 1966, стр. 53):

                                            (4.8.),

где * - концентрационный коэффициент активности противоиона и избыточной работы по переносу иона из дисперсионной среды (свободные диполи) на поверхность сольватного слоя (связанные диполи):

                                           (4.9.),

где ₀ – единый нулевой коэффициент активности противоионов.

Таким образом, избыточная суммарная работа переноса противоиона будет:

                                         (4.10.),

где:

                                               (4.11.).

Подставив уравнения (4.7.) и (4.10.) в (4.6.), получим основное трансцендентное уравнение:

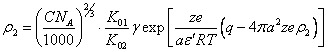               (4.12.).

Из уравнения (4.12.), как частный случай, можно найти условие, при котором плотность противоионов на поверхности сольватного слоя максимальна, а, следовательно, максимальна эффективность соударения частиц, поскольку количество освобожденных диполей на поверхности сольватного слоя пропорционально количеству адсорбированных противоионов.

Отсюда, для порога коагуляции можно записать условие:

                                           (4.13.).

Уравнение (4.12.) при условии (4.13.) примет вид:

                                        (4.14.).

Приняв зависимость между ln и C по теории Дебая-Хюккеля (Н.А. Измайлов. Электрохимия растворов. М., 1966, стр. 106):

                                         (4.15.)

и подставив ее в (4.14.), найдем условие для порога коагуляции:

;      =0,263                                 (4.16.).

Уравнение (4.16.) следует рассматривать как критерий устойчивости коллоидных систем. Результат, полученный в этом уравнении, не зависит от вида уравнения (4.7.).

Воспользовавшись критерием устойчивости (4.16.) можно найти критерий устойчивости гидрозолей. Для этого необходимо определить значение диэлектрической постоянной на поверхности гидратного слоя коллоидных частиц.

По данным многих исследователей толщина сольватного слоя колеблется от 100 до 2000 ангстрем. Большинство исследователей приводят для гидратного слоя цифру около 350-400 A⁰. Диэлектрическая постоянная воды меняется в зависимости от толщины пленки от 4,5 при толщине 70 A⁰ до 75 при толщине 1600 A⁰ , значение для свободной воды 80 достигается при толщине пленки 37000 A⁰. При интерполяции этих данных толщине пленки в 350-400 A⁰ соответствует диэлектрическая постоянная воды около 40. Тогда, принимая величину диэлектрической постоянной равной 40 на поверхности гидратного слоя, что соответствует «полусвязанным» диполям воды, из приложения к монографии (Н.А. Измайлов. Электрохимия растворов. М., 1966) найдем приблизительное экспериментальное значение ₀: lg₀ 0,45, ₀ 2,82. После подстановки (4.16.) в (4.11.), получим при пороге коагуляции гидрозолей:

                                 (4.17.).

Если подставить (4.17.) в уравнение Дебая-Хюккеля для коэффициента активности ионов, то получим выражение для концентрации электролита при пороге коагуляции.

Уравнение (4.17.) известная эмпирическая закономерность, обнаруженная Освальдом на сотнях опытов и следствия из нее подробно обсуждены в его работе (В. Освальд. Успехи химии, 9, #5,1940). Критерий устойчивости, определяемый уравнением (4.16.) можно назвать обобщенным правилом Освальда. Этот критерий учитывает как свойства дисперсионной среды, так и свойства сольватного слоя коллоидных частиц и, следовательно, связан со свойствами вещества этих частиц. Учитывая выражение (4.10.), можно сформулировать этот критерий в несколько ином виде: коллоидная система будет обладать минимальной устойчивостью к агрегированию, когда энергия активации адсорбции противоионов на треть больше их тепловой энергии.

В частном случае лиофобных золей, полученный критерий устойчивости переходит в правило Освальда. Например, изучая коагуляцию золей серы (С.Е. Харин, И.В. Чайковская. Коллоидный журнал. 18, 350, №3, 1956) авторы нашли подтверждение правилу Освальда: *=const=0,73.

Вид соотношения (4.16.) показывает, что оно может быть применено к общему случаю адсорбции ионов из растворов электролитов на поверхность адсорбента, когда энергия активации десорбции является некоторой функцией от количества адсорбированных ионов (что почти всегда имеет место). В этом общем случае мы получим тот же результат: максимум адсорбции наблюдается при ln=-4/3, где =*/₀. Физический смысл этого результата состоит в том, что при малой концентрации электролита ионы сильней удерживаются на поверхности адсорбента, чем в растворе, а при большой концентрации взаимодействие ионов с раствором сильней, чем с адсорбентом.

5. Магнитная обработка воды

Первые сведения о влиянии магнитов на свойства воды идут из медицины, начиная с XIII века (женевский физик де Герсю). Наиболее систематизированные сведения получены с 30-х годов XX века Джорджио Пиккарди, который на основании более 250 тыс. наблюдений установил статистически достоверную связь между активностью Солнца и скоростью оседания в воде золя оксихлорида висмута (получаемого гидролизом трихлорида висмута). В 1945 году бельгийский инженер Т. Вермайер запатентовал способ борьбы с накипью посредством магнитной обработки воды, содержащей соли жесткости. Этот способ - один из наиболее воспроизводимых и эффективных практических приложений магнитной обработки, поэтому он наиболее полно изучен. В основе эффекта лежит улучшение условий выпадения кристаллов солей жесткости из нагреваемой воды не на твердых стенках, а в объеме воды. При этом в 5 раз увеличивается число кристалликов и во столько же раз уменьшается их размер. Размер, конечно, не может уменьшиться во столько же раз, во сколько раз увеличилось число кристаллов, иначе появится дефицит общей массы выделившихся кристаллов, а значит изменится термодинамическое равновесие реакции, что маловероятно. Возможно это противоречие снимется тем, что после магнитной обработки из воды выпадают кристаллы не кальцита, а арагонита (по данным A.M. Крапивина и др.). В данном случае оценка правильности данных не столь важна, т.к. ниже будет приведено достаточное количество противоречивых экспериментальных данных. В большинстве случаев хорошие результаты получаются, если вода относится к кальциево-карбонатному классу.

После открытия Вермайера начался поистине "магнитный бум" в среде "прикладников". Практические результаты не замедлили сказаться, но вместе с тем сама идея магнитной обработки воды все больше дискредитировала себя в глазах ученых, поскольку в отсутствие научного объяснения наблюдаемых эффектов в литературе стали появляться противоречивые с научной точки зрения экспериментальные данные. Сейчас дело дошло до того, что каждый может получить посредством магнитной обработки то, что ему нужно. Приведу несколько примеров.

1. Часто уже после контакта ранее имевшейся накипи с омагниченной водой накипь начинает растворяться и отваливаться от стенок, причем по данным Татаринова магнитная обработка ускоряет растворение в 5 раз, а по данным Скоробогатова скорость растворения MgS0₄ увеличивается в 120 раз. Это противоречит выше приведенным данным из которых следует, что магнитная обработка способствует не увеличению, а уменьшению растворимости солей жесткости. Выход из приведенного противоречия, по-видимому, в плохой "чистоте" экспериментов в отношении поглощения системой во время обработки посторонних газов (в данном случае CO₂). Так например, смешение раствора азотнокислого свинца с раствором едкого калия приводит к образованию гидроокиси свинца, а после омагничивания соли свинца - к образованию карбонатов свинца из-за повышения концентрации СО₂ в растворе. Правда, неизвестно, возможно авторы во втором случае брали "старый" едкий калий, который, как известно, поглощает CO₂ из воздуха с образованием углекислого калия. В то же время есть независимые данные (Корюкин, Классен) об увеличении содержания кислорода и углекислого газа в обработанной воде, например, из-за увеличения концентрации O₂ в омагниченной воде, скорость окисления пирита FeS₂ в воде возрастает на 20%. Однако, растворимость газов, как величина термодинамическая не должна изменяться и поэтому указанные эффекты следует рассматривать как увеличение скорости растворения газов в обработанной воде. Тогда можно сделать вывод, что омагниченная вода сама по себе ускоряет растворение веществ в том числе и газов, а уменьшение растворимости солей жесткости связано с влиянием увеличенного содержания СО₂ в водах, обработанных для предотвращения накипи.

2. Обнаружено, что смачивающая способность воды после обработки уменьшается. Но для поверхностей содержащих кремний она увеличивается. Классеном установлено, что пылеулавливающая способность (породная и угольная пыль) обработанной воды в 3 раза выше, что противоречит его же данным об ухудшении смачивающей способности обработанной воды. При нагнетании воды в пласт угля она распространяется там почти вдвое дальше, т.е. смачивающая способность воды улучшается. Из этого противоречия пока не видно выхода.

3. Гребнев, Классен и др. установили, что магнитная обработка повышает скорость адсорбции поверхностно-активных веществ на твердых поверхностях и на разделе вода-воздух. Соложенкин и др. установили, что адсорбция красителей на волокне увеличивается на 42%, а Татарников и др. нашли, что омагниченная вода на 40% ускоряет отмывку волокна от диметилформамида. Лиакумович считает, что омагниченная вода лучше отмывает материалы от примесей. Тоже неразрешимое экспериментальное противоречие.

Приведу еще краткие примеры, показывающие насколько запутан этот вопрос в результате чего экспериментаторы "достигают'' того к чему стремятся, решая, зачастую, прямо противоположные задачи одним и тем же способом.                                            

При добыче обводненной нефти в трубы помещают магниты, в результате отложение солей уменьшается в 6-12 раз, а старые отложения разрушаются. При затворении цемента омагниченной водой прочность его увеличивается, получается более мелкозернистая структура, в 2,5 раза уменьшается газопроницаемость цементного камня.

Обработка повышает прочность песчано-глинистых форм для литья и одновременно увеличивает их газопроницаемость.

Обработка воды, на которой замешивается масса для формовки кирпича, увеличивает его прочность и уменьшает пористость.

Обработка пульпы при флотации увеличивает извлечение меди и золота, увеличивается сорбционная емкость ионитов, на 20-30% возрастает емкость поглощения сульфоугля.

Верижская нашла, что скорость взаимодействия кислот с металлами возрастает примерно в 2 раза после обработки, но при некоторой напряженности магнитного поля взаимодействие резко замедляется.

При производстве каустической соды на 6% увеличивается степень каустификации.

Снижается в 3 раза удельный расход алмазов при шлифовании, во много раз увеличивается стойкость водно-масляной эмульсии.

Скалозубов, Кукоз и Чернов нашли даже, что при производстве соды в 2 раза изменяется константа равновесия реакции с уменьшением в 2 раза концентрации соды в осветленном растворе, чему вообще трудно поверить, т.к. это противоречит термодинамике.

Из рассмотрения всей в настоящее время полученной экспериментальной "каши" вытекает необходимость выделения сравнительно достоверных опытных данных и простых для анализа систем:       

1. Магнитная обработка способствует растворению в воде углекислого газа и кислорода, увеличивает скорость растворения веществ.

2. Обработанная вода биологически активна.

3. Ускоряются коагуляционные процессы.

Во втором случае система настолько сложна, что приходится сделать вывод только о том, что омагниченная вода чем-то отличается от обычной.

Перейдем к вопросу о том, какие условия необходимы для проявления эффекта. При этом также отбросим все сколько-нибудь сомнительные или одиночные данные.

1. Наличие примесей.

Для чистой воды эффекты не наблюдаются. В общем случае изменение свойств воды после магнитной обработки возрастает с увеличением концентрации примесей в некоторых пределах. Большую роль играет характер примесей. Духанин пришел к выводу, что информацию несет сама вода, а ионы усиливают или ослабляют проявляемый эффект. Общий вывод по 1 пункту пока сделаем такой: или изменяются свойства воды самой по себе, а ионы как то выявляют эти изменения, или эти изменения воды возможны только при наличии ионов, или вода не при чем и играют роль только ионы.

2. Течение обрабатываемой системы в магнитном поле.

Если нет перемещения относительно поля эффект не наблюдается. При течении возникают только лоренцовы силы. Общий вывод по 2 пункту. Действие проявляется только в тех системах, где могут возникнуть лоренцовы силы (диполи, ионы, заряженные коллоидные частицы и т.д.).

3. Скорость потока.

Для проявления эффекта в полной мере нужна оптимальная скорость потока. С увеличением скорости эффект увеличивается, затем падает. Этот пункт очень важен по своему информативному значению, т.к. показывает, что для проявления эффекта необходимо сравнительно большое время обработки. Вывод первого пункта остается только в редакции Духанина, поскольку известно, что химические реакции между ионами в растворе идут практически мгновенно. Но здесь следует добавить, что макроперемещение ионов под действием лоренцовых сил, требующее длительного времени не может также дать кривую с максимумом. Из вывода 2-го пункта остается действие лоренцовых сил на диполи воды (для чистого раствора) и ионы в том смысле, что они могут как-то влиять на поведение диполей.

4. Частота изменения поля.

Наиболее сильно действует на воду низкочастотная обработка: единицы или десятки герц (это как раз соответствует потоку со скоростью 1 м/сек в зазоре длиной 10 см). Вывод по п. 4 тот же, что и по п. 3: для образования омагниченной воды нужно время.

5. Напряженность поля.

Эффект обработки в зависимости, от напряженности поля находится в полиэкстремальной зависимости и, во всяком случае, немонотонной. С одной стороны, это могло бы быть объяснено тем, что в процессе обработки имеется, по крайней мере, один препятствующий фактор. С другой стороны, коагуляционные процессы, например, не монотонно зависят от концентрации коагулирующего электролита. Напомним, что надежный эффект действия магнитного поля так или иначе связан с коагуляционными процессами в обрабатываемой системе.             

6. Время релаксации.

Самопроизвольное возвращение водных систем после магнитной обработки в исходное состояние занимает по времени диапазон от нескольких десятков минут до нескольких суток по данным разных авторов. Увеличение температуры ускоряет процесс релаксации. Отсюда можно сделать вывод, что вызванные в системе изменения термодинамически не устойчивы, но процесс релаксации встречает значительные кинетические затруднения.                                            

Поскольку теории явления нет, перейдем к рассмотрению существующих в настоящее время гипотез, недостатка в которых нет.

1. "Коллоидные" гипотезы. В их основе лежит действие магнитного поля на коллоидные частицы, обладающие довольно большой магнитной восприимчивостью (пара- или ферромагнитные) и всегда присутствующие в воде. Поэтому чистая вода не омагничивается.     

Против этого рода гипотез говорит тот факт, что омагниченная вода постепенно теряет свои свойства, т.е. эффект обратим, в то же время, коллоидные процессы необратимы.

2. "Ионные" гипотезы в которых основная ответственность возлагается на ионы находящиеся в воде. В основе лежит действие магнитного поля на перемещающиеся ионы. Большинство сторонников подчеркивают большую роль влияния магнитного поля на гидратацию ионов (гидратация уменьшается). В доказательство приводят увеличение на 20-40% сорбционной емкости ионитов. Методом ЯМР (по сужению ширины линии сигнала ЯМР воды) показано, что гидратация ионов уменьшается после магнитной обработки. Кстати, сторонником этих гипотез является Классен.

Против ионных гипотез энергетический фактор, поскольку энергия гидратации ионов сравнима с потенциалом ионизации соответствующих атомов. В то же время, энергия, сообщаемая воде магнитным полем напряженностью 1000 эрстед на 5-6 порядков меньше энергии теплового движения молекул воды. Кстати, это основной аргумент критиков, полностью отрицающих на его основании какие-либо эффекты при омагничивании воды. Представьте себе карточный домик, разрушающийся от малейшего дуновения, который стоит преспокойно при урагане - примерно так выглядит соотношение между энергией, полученной молекулами воды при омагничивании и тепловой энергией молекул воды.

3. "Водяные" гипотезы, обосновывающие действие магнитных полей на собственно воду. Основаны на возможности изменения свойств воды в зависимости от степени и характера ассоциации ее молекул.

Например, Киргинцев развил гипотезу о диспергирующем действии магнитного поля на агрегаты молекул воды. Изменение крупности агрегатов не вызывает значительного изменения свободной энергии воды, значит не требует затраты большой энергии. Механизм диспергирующего действия не раскрывается. Многие исследователи говорят о "структурной памяти" воды, побывавшей в магнитном поле.

К сожалению, существующие в настоящее время гипотезы столь расплывчаты, что их невозможно проверить в условиях "большого риска" и, следовательно, пока нельзя надежно подтвердить или опровергнуть.

Методы контроля степени омагниченности воды очень опосредованы. Более или менее легок для интерпретации водно-спиртовый тест Шахова, фиксирующий степень уменьшения объема смеси воды и спирта по сравнению с их частными объемами. По его свидетельству омагничивание воды значительно уменьшает объем смеси воды и спирта. Кстати, если это наблюдение надежно, то оно указывает на такие изменения, которые возможны только при внешнем давлении на смесь в сотни тысяч атмосфер.

Гипотеза автора.

Рассмотрим теперь мою гипотезу о влиянии магнитного поля на водные системы.                      

Коллоидные частицы окружены сольватным слоем толщиной, порядка 300 Å образованным ориентированными диполями воды. Этот слой образуется только при наличии небольшого количества ионов в дисперсионной среде, которые, адсорбируясь на поверхности частицы, создают условия для термодинамической устойчивости сольватного слоя (потенциалоопределяющие ионы). Противоионы адсорбируются тонким слоем на поверхности сольватного слоя, который обладает такими свойствами, что они не проникают к поверхности частицы. О прочности этого слоя можно судить по тому, что при коагуляции (слипании частиц) коллоидного раствора, сближение ядер продолжается длительное время (в некоторых случаях месяцы и годы). Противоионы частью расположены в сольватном слое, а частью в прилегающем к частице растворе. При броуновском движении частицы, поверхность скольжения лежит внутри слоя противоионов, поэтому частица оказывается заряженной (чаще отрицательно), обладая некоторым электрокинетическим потенциалом. В целом такая частица называется мицеллой. Сольватный слой представляет собой "третью фазу" коллоидной системы (см. фигуру 5.1.).

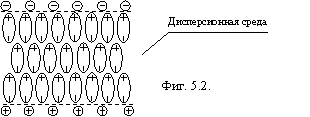
В омагниченной воде под действием силы Лоренца образуются пластинчатые домены ориентированных молекул воды, стабилизированные ионами (фиг. 5.2.).

При этом нужно отметить существенное обстоятельство: магнитное поле не "работает", а лишь провоцирует образование этих доменов, т.е. играет роль "спускового крючка" (на такую роль магнитного поля указывал академик Вонсовский). При образовании доменов (лучше их назвать аквацеллами, чтобы не путать с магнитными доменами) энергия выделяется. После снятия поля аквацеллы, как "третья фаза" постепенно растворяются, а может быть, агрегируются между собой с убыванием счетной концентрации их.

Приведем некоторые расчеты, пользуясь описанной моделью.

1. Сравним электрореологический эффект с сольватным слоем. Коллоидные частицы имеют -потенциал ~150 mV, а в гипотетическом случае без противоионов порядка 300 mV или 0,3 в. Толщина сольватного слоя ~300 Å, отсюда напряженность электрического поля при которой сольватный слой становится термодинамически устойчивым составит 10⁷ в/м. Электрореологический эффект проявляется при напряженности поля 10⁶ в/м и обладает свойством насыщения при напряженностях порядка 10⁷ в/м. Таким образом, электрореологический эффект вызван разворотом диполей в сольватном слое коллоидных частиц.

2. Подсчитаем, каково должно быть магнитное поле, чтобы вызвать эффект на уровне электрореологического.

При электрореологическом эффекте на один двойной заряд диполя воды действует ориентирующая сила 4·10^-15 н, а сила Лоренца при магнитной обработке (1 м/сек. 1000 э) 3·10^-20 н. Таким образом, нужно в 10⁴-10⁵ раз усилить магнитное поле, чтобы получить эффект на уровне электрореологического. Чтобы полностью смоделировать структуру сольватного слоя напряженность магнитного поля надо усилить в 10⁶ раз. Здесь необходимо добавить, что сольватный слой коллоидных частиц образуется за время от нескольких минут до нескольких часов, то же время нужно выдержать систему при действии внешнего магнитного поля. При этом обрабатываемая водная система должна "затвердеть" - настолько высоки механические свойства сольватного слоя коллоидных частиц.

3. Найдем энергию образования сольватного слоя из теплоты смачивания дисперсных тел ~60 кал/г. Если принять частицы ~1 мкм, толщина слоя 300 Å, то получается ~12 ккал/моль. Та же энергия выделяется и при омагничивании воды.                                           

4. Оценим концентрацию аквацелл при обычных условиях магнитной обработки, считая, что увеличение температуры при обработке незаметно и сравнимо с ее увеличением от трения при движении в магнитном зазоре (~0,1 ⁰С). Получается 0,01% весовых. Реальная концентрация может быть и того меньше, хотя счетная концентрация аквацелл, зависящая от их величины может быть очень большой при их малом размере.

Проведем качественную оценку гипотезы.

1. Наличие примесей.

В гипотезе очень важную роль играют ионы в воде. Совершенно чистая вода содержит ионы водорода и гидроксила в концентрации, вполне достаточной для проявления эффекта "памяти", но и ионы примесей, начиная с концентрации, порядка 10^-8 моль/л способствуют возникновению эффекта. С другой стороны, слишком большое количество ионов при концентрациях порядка порога коагуляция коллоидов может, но не всегда привести к исчезновению "памяти". Из гипотезы ясно, что в отсутствие примесей вода будет мгновенно релаксировать при снятии поля. При наличии примесей поле, стабилизирующее аквацеллы, все равно остается. В зависимости от природы и концентрации примесей эффект будет различным.  

2. Течение обрабатываемой системы в магнитном поле.

Это очевидное и необходимое условие для ориентации диполей воды. Идеальный случай - максимальная скорость течения и возможно большая длина магнитного зазора.

3. Скорость потока.                     

Чем выше скорость, тем лучше, но при сохранении того же времени нахождения системы в поле. В магнитах конечных размеров при больших скоростях время обработки будет слишком мало для образования аквацелл. Чтобы этого избежать, обработку лучше проводить в кольцевых сосудах, аналогичных ускорителям частиц.

4. Частота изменения поля.

Идеальный случай, когда поле вообще не меняется, но при существующих конструкциях магнитов это пока невозможно, поэтому необходима минимально возможная частота.

5. Напряженность поля.

От напряженности магнитного поля наблюдается  полиэкстремальная зависимость. Вызвано это тем, что при образовании аквацелл ионы мешают, т.к. лоренцовы силы их передвигают не туда, куда надо. Поэтому ионы лучше вносить после образования аквацелл, но здесь мешает малое время релаксации нестабилизированных аквацелл. Тем не менее, Соколов наблюдал, что эффект почти одинаков, если вносить соли железа в обрабатываемую воду до или после обработки, а Шахов и др. нашли, что введение в воду коагулянта полезней после обработки. По-видимому, в обоих случаях в системах уже было некоторое количество стабилизирующих ионов. Кроме того, под действием лоренцовых сил происходит скопление противоположно заряженных ионов так, что возникает электрическое поле, ориентирующее ионы в противоположную магнитному полю сторону. И, наконец, уже сформировавшиеся аквацеллы могут разворачиваться в магнитном поле целиком и разрушаться, поскольку на диполи действует ориентирующий момент в одну сторону, а на стабилизирующие ионы в другую. Отсюда полиэкстремальность эффекта от напряженности поля не удивительна.

6. Время релаксации.

Различное время релаксации обусловлено различным стабилизирующим действием ионов в зависимости от их концентрации и природы. В сольватных слоях коллоидных частиц в отсутствие коагуляции это время не ограничено, т.е. слой термодинамически устойчив. Известно, что многие нерастворимые в воде вещества, особенно, высокомолекулярные (например, полиэтилен) "растворяются" глобулярно, образуя не истинный раствор, а высокодисперсную коллоидную взвесь. Подобные вещества должны стабилизировать омагниченную воду. Кроме того, маловероятно, что аквацеллы представляют собой плоские или нитеобразные агрегаты из-за высокой поверхностной энергии. Более вероятно их существование в свернутом в сферу виде. Тогда они будут представлять собой точную копию коллоидной частицы без твердого ядра в центре.

7. Плохая воспроизводимость экспериментов.       

По-видимому, она вызвана тем, что исходный для обработки объект содержит разное количество зародышей аквацелл. В совершенно чистой от аквацелл системе во время обработки они могут не образовываться вовсе по аналогии, например, с переохлажденной жидкостью в которой не образуется кристаллов в отсутствие зародышей или поверхностей раздала фаз. Этот момент играет, видимо, очень большую роль, учитывая из вышеизложенного, что существующие способы обработки очень далеки от идеала.

Существует еще один существенный фактор резко снижающий воспроизводимость экспериментов с "памятью" воды. Процесс взаимного усиления ориентации молекул в аквацелле и адсорбции ионов на ее поверхности нарастает, как снежный ком, поэтому малейшее изменение внешних условий сильно на него влияет. Кроме того, при броуновском движении аквацелл почти каждое их сближение приводит к затягиванию в пространство между ними одноименно заряженных ионов (из-за влияния противоионов). При удалении аквацелл друг от друга между ними оказывается вновь рожденная аквацелла того же знака заряда, т. е. аквацеллы способны размножаться в благоприятных условиях. Этот эффект для биологии имеет очень важное значение, т.к. живые организмы, в основном, состоят из воды и имеют постоянно действующие генераторы аквацелл в виде частиц крови и других коллоидных частиц.

Разбавление раствора, содержащего аквацеллы, может при соответствующих условиях не только не уменьшить их количества в растворе, но концентрация их может даже расти, если разбавление происходит достаточно медленно, чтобы вода могла хорошенько ''запомнить" свою структуру. В этой связи становятся понятными некоторые совершенно удивительные эксперименты, связанные с "памятью'' воды. Некоторые биологически активные вещества, будучи разбавляемые в водных растворах сохраняют свою активность. Все было бы ничего, но дошлые экспериментаторы настолько разбавили раствор, что в сосуде не осталось ни одной молекулы вещества... а активность осталась! Вода "запомнила", что в ней было растворено.               

Эксперимент автора.

Таким образом, в первом приближении, омагниченную воду можно представить себе как суспензию механически прочных пластинок водных ассоциатов (аквацелл) с той особенностью, что эти ассоциаты, слипаясь между собой противоположно заряженными поверхностями, вначале укрупняются, затем "растворяются". Проще всего наличие аквацелл, очевидно, обнаружить фильтрованием омагниченной воды. Эффект омагничивания должен проявиться в уменьшении скорости фильтрации при закупоривании пор фильтра водными ассоциатами.

В описанных ниже опытах были использованы фильтры "синяя лента", предварительно замоченные в дистиллированной воде в течение получаса. Водопроводную воду выдерживали сутки при комнатной температуре и омагничивали (1 м/сек, 1000 э). Через определенное время отбирали порцию (100 мл) и фильтровали. Скорость фильтрации отмечали через 2 минуты после начала фильтрации. На фигуре 5.3. представлены результаты трех параллельных опытов в зависимости от времени после омагничивания. Треугольниками отмечены результаты фильтрации водопроводной воды, пропущенной через магнитный зазор в отсутствие тока в электромагните (контроль). Каждая точка на графике соответствует фильтрованию новой порции воды через свежий фильтр.

Из фигуры видно, что непосредственно после обработки образуются аквацеллы свободно проходящие через фильтр с размером менее 1-3 микрон, которые агрегируются и уже через 10 минут после обработки достигают размеров достаточных для того, чтобы забивать поры фильтра, что приводит к резкому уменьшению скорости фильтрации. В дальнейшем агрегаты становятся или слишком большими (не проникают в поры фильтра) или, наоборот, очень малыми вследствие разрушения. Скорость фильтрации вновь возрастает. По результатам этого опыта можно оценить счетную концентрацию аквацелл, образующихся после омагничивания воды, приняв их размер равным 1х1х0,1 мкм. Она оказалась не менее миллиарда аквацелл в 1 см³.

Был проведен и такой опыт: непосредственно после обработки водопроводная вода отфильтрована, при этом скорость фильтрации уменьшилась всего на 6% (в пределах ошибки опыта), затем фильтрат через 5-7 минут был вновь отфильтрован. Скорость фильтрации уменьшилась уже на 34%, очевидно, за счет укрупнения аквацелл, прошедших через фильтр при первой фильтрации.

Резюме

Магнитное поле не "работает", а лишь провоцирует образование водных ассоциатов, т.е. играет роль спускового крючка. При образовании аквацелл энергия не поглощается, а выделяется. Строение их можно себе представить как сольватный слой коллоидных частиц развернутый в плоскость или свернутый в сферу. После образования аквацеллы коагулируют, укрупняются, нейтрализуется стабилизирующий заряд на их поверхности, ориентированная структура водных ассоциатов становится неустойчивой и постепенно аквацеллы разрушаются.

Из-за невысокой концентрации аквацелл такие свойства омагниченной воды, как вязкость, плотность, теплота испарения и т.п. практически не изменяются. В то же время, содержащиеся в ней аквацеллы будут оказывать большое влияние на процессы, связанные с образованием новых фаз, адсорбцией, коагуляцией, а также в биологических системах.

Автор надеется, что изложенная гипотеза поможет заинтересованным исследователям регулировать концентрацию аквацелл в воде от максимальной до нулевой, т.е. познать секреты "живой" и "мертвой" воды.

6. Ступенчатость процессов в мире на примере коагуляции коллоидных систем.

Ступенчатость процессов в мире мы наблюдаем всегда и везде. Наблюдая любое явление можно гарантированно утверждать: «все пройдет, пройдет и это».

Характерной особенностью этапности, обеспечивающей прогресс, является то обстоятельство, что каждый последующий этап существенно или принципиально отличается от предыдущего этапа.

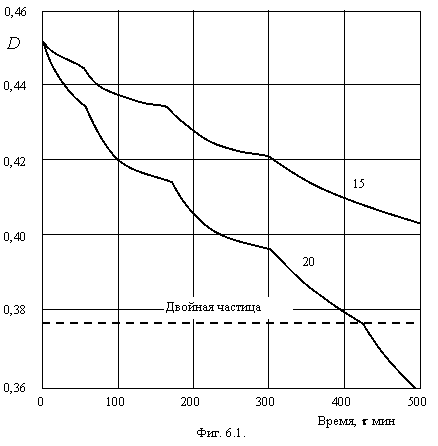
При коагуляции коллоидных систем ступенчатость этого процесса проявляется отчетливо при эффективности столкновений частиц меньше единицы (медленная коагуляция). Наши опыты по медленной коагуляции анатаза (модификация двуокиси титана) в 25 ммоль/л растворе KCl показали перелом кинетической кривой в точке D=0,3747 (D₀=0,4535). Этот перелом соответствует образованию двойных частиц по всему объему суспензии. Действительно, по уравнению (2.1.1.) этого раздела книги, оптическая плотность при двойной частице D₂=0,3779, что с точностью 0,85% совпадает с экспериментом. Анализ большого числа литературных данных подтверждает ступенчатость процесса коагуляции. Мои опыты однозначно показывают, что процесс медленной коагуляции идет таким образом, что вначале во всей системе образуются двойные частицы, затем четверные и т.д. Это указывает на приложимость правила фаз Гиббса к процессу коагуляции частиц, причем двойные, четверные и т.п. частицы следует рассматривать как отдельные «фазы» системы.

На фигуре 6.1. представлены кинетические кривые коагуляции суспензии двуокиси титана при концентрации хлористого калия меньше пороговой. Цифры у кривых – концентрация KCl в ммоль/л.

Как видно из фигуры 6.1. на этих кривых отчетливо наблюдаются переломы до двойной частицы. Это удалось зафиксировать из-за отсутствия перемешивания раствора и высокой чувствительности метода измерения. Невозможно объяснение этих переломов изменением состояния двойного электрического слоя коллоидных частиц из-за большого времени коагуляции, при котором наблюдаются переломы. Изломы кинетических кривых, по-видимому, следует отнести к ступенчатому изменению коагуляционной способности частиц, связанной с изменением состояния их сольватного слоя имеющего, очевидно, сложную структуру и состоящего из нескольких подслоев (в нашем примере 3), обнажающихся по мере разрушения сольватного слоя проникающими в него противоионами. Значительная прочность сольватного слоя частиц анатаза подтверждается большим промежутком времени, после которого наблюдаются переломы. В пользу этого утверждения говорит тот факт, что переломы наблюдаются при определенном времени коагуляции. Ионы калия проникают внутрь сольватного слоя и нарушают его структуру. Скорость диффузии ионов в случае, относящемся к фигуре 6.1. практически не зависит от концентрации их в объеме коллоидного раствора и вместе с высокой монодисперсностью коллоидных частиц приводит к переломам кинетической кривой к определенному моменту времени.

При концентрации электролита ниже пороговой, процесс коагуляции определяется величиной отталкивания, связанной с зарядом частиц. Равновесные агрегаты не могут достигать больших размеров, т.к. между частицами агрегата действуют значительные электростатические силы отталкивания. По мере уменьшения заряда частиц с увеличением концентрации электролита, равновесный размер агрегатов растет. До порога коагуляции получаются плотные агрегаты некристаллического типа, т.к. такое агрегирование малого числа частиц энергетически выгодно. При наличии остаточного электростатического барьера, частицы не остаются на месте их первого соприкосновения, а занимают наиболее энергетически выгодное положение.

В работе (А.А. Штернберг. Сборник статей: Рост кристаллов. т.5, М., 1965, стр. 179) показано, что наиболее устойчивым образованием некристаллического типа является икосаэдр, содержащий 13 частиц. Плотность упаковки частиц в таком агрегате очень высокая и не имеет аналогов в кристаллических структурах с плотнейшей упаковкой частиц.

Когда концентрация электролита превышает пороговую, энергетический барьер становится столь малым, что частицы в агрегате остаются в положении их первого соприкосновения. Это приводит к образованию квазикристаллических нитеподобных, плоских и объемных агрегатов с малой плотностью. Не сферическая форма агрегатов легко фиксируется, если в кювете оставить маленький пузырек воздуха не попадающий на считывающий луч света и перемешивающий раствор при вращении кюветы. При этом агрегаты ориентируются поперек светового луча, и оптическая плотность меняется при повороте кюветы на 180⁰ так сильно, что самописец пишет кривую шириной почти на половину своей шкалы.

В результате экспериментов выяснилась следующая картина медленной коагуляции. Сначала по всей системе образуются агрегаты из двойной частицы. Только после завершения этого процесса начинается коагуляция двойных частиц между собой с образованием агрегатов из 4 частиц. Далее процесс идет аналогичным образом, и образуются агрегаты из 8 частиц. После этого наблюдается удивительное явление. Агрегаты из 8 частиц слипаются вместе с образованием агрегата из 16 частиц, внутри этого агрегата быстро образуется икосаэдр из 13 частиц, электростатическое отталкивание для «лишних» трех частиц становится таким, что они покидают агрегат. Процесс очень напоминает распад ядра с избытком протонов.

Чтобы проверить, имеет ли обнаруженное явление всеобщий характер или относится только к частному случаю, эксперименты были проведены с гидролизом производственных растворов титанилсульфата с содержанием TiO₂ 200 г/л. В связи с тем, что предгидролизный раствор представляет собой темнокоричневую жидкость с сильным поглощением света в первой серии опытов производственный раствор пришлось разбавлять дистиллированной водой до 6-36 г/л TiO₂. При концентрации двуокиси титана выше 30 г/л кинетические кривые имеют S-образную форму с индукционным периодом, которые имеют место в реальном производственном процессе производства пигментной двуокиси титана.

По результатам опытов выяснен следующий механизм гидролиза. Вначале образуются кристаллиты метатитановой кислоты величиной 40-50 Å (по нашим данным рентгенографического анализа они в дальнейшем практически не увеличиваются в размерах). Затем эти кристаллиты коагулируют попарно по всей системе, далее пары собираются в тетраэдры, которые в дальнейшем образуют агрегаты из 8 частиц. Затем при коагуляции они перестраиваются, образуя икосаэдр из 13 частиц, выбрасывая лишние 3 частицы. Размер икосаэдра составляет в поперечнике 100 Å, т.е. равен радиусу действия ван-дер-ваальсовых сил для кристаллитов метатитановой кислоты, который мы определили из опытов пептизации этой кислоты триэтаноламином. Далее икосаэдры соединяются в пары, а затем пары образуют тетраэдр из 4 икосаэдров. Эти агрегаты, содержащие 52 исходных кристаллита оказываются очень устойчивыми к дальнейшему агрегированию и в технологических растворах коагулируют только во время подачи воды в конце гидролиза.

Для проверки того, что коагуляция кристаллитов метатитановой кислоты является основной чертой гидролиза, производственный раствор разбавляли не дистиллированной водой а 0,8% раствором агар-агара до концентрации 36 г/л TiO₂. За время наблюдения в течение 18 часов изменения оптической плотности раствора не обнаружено. Этот опыт показал, что в условиях, когда подвижность ионов не изменилась, а коллоидные частицы потеряли подвижность (раствор консистенции густого киселя), процесс гидролиза (агрегирования частиц) прекращается.

Начальный участок кинетических кривых гидролиза идет с ускорением. Это обусловлено тем, что силы Ван-дер-Ваальса являются аддитивными и по мере увеличения числа частиц в агрегате притяжение между агрегатами возрастает. При достижении размера агрегатов равным радиусу действия этих сил (икосаэдр 100 Å) дальнейшее увеличение размера не приводит к увеличению сил притяжения. Следовательно, образование икосаэдров должно наблюдаться вблизи точки перегиба кинетической кривой гидролиза, что подтверждается экспериментально (таблица 6.1.).

Таблица 6.1.

Оптическая плотность раствора (36 г/л TiO₂) в точках перелома кинетической кривой гидролиза.

№	Обозначение точек кинетической кривой	эксп.	теор. по (2.2.5.)	Примечание
1	Начало горизонтального участка	0,0118	0,0116	Тетраэдр из 4 икосаэдров
2	Перед горизонтальным участком	0,0083	0,0082	Двойной икосаэдр
3	В точке перегиба кривой	0,0066	0,0065	Икосаэдр из 13 кристаллитов
4	Точки излома кривой от индукционного периода до точки перегиба кривой	0,0039	0,0040	8-ная частица
5		0,0019	0,0020	Тетраэдр из кристаллитов
6		0,0009	0,0010	Агрегат из двух кристаллитов
7		0,0005	0,0005	Одиночные кристаллиты

На электронномикроскопических снимках образцов метатитановой кислоты с горизонтального участка кинетических кривых хорошо видны тетраэдры из 4 икосаэдров. Количество кристаллитов в икосаэдре трудно точно подсчитать из-за предельного увеличения.

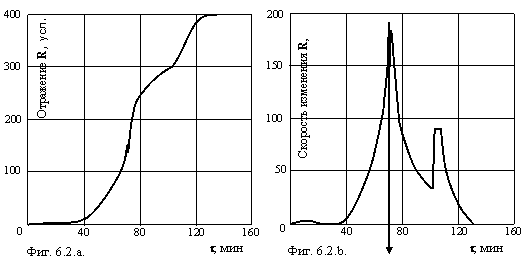
Для проверки сделанных выводов на реальных технологических растворах были поставлены эксперименты с термическим гидролизом раствора, содержащего 206 г/л TiO₂. На установке фиксировали процесс гидролиза, измеряя не пропускание света, а отражение его от раствора, находящегося в стеклянном цилиндрическом сосуде. Условия гидролиза строго соответствовали регламентным указаниям на проведение этой операции в производстве пигментной двуокиси титана. Запись кинетической кривой производили одновременно двумя самописцами EZ-2, один из которых записывал интегральную кривую, другой – дифференциальную. Всего было проведено 6 гидролизов, чтобы убедиться, что полученный эффект не является случайностью. Поскольку воспроизводимость опытов была высокой, на фигуре 6.2. приведена кинетическая кривая в интегральной (a) и дифференциальной (b) форме, одинаковая для всех проведенных опытов.

Обращает на себя внимание резкое уменьшение отражательной способности раствора около точки перегиба кинетической кривой гидролиза, причем этот скачок совершается за время менее секунды, о чем говорит столь высокое отрицательное значение производной, что его не удалось зафиксировать даже при наличии на самописце 11 запасных шкал (общая высота линии со стрелкой на фигуре 6.2.b. более 4 метров). После скачка процесс идет с меньшего значения интенсивности рассеянного света и с меньшей скоростью.

Автор берет на себя смелость утверждать, что икосаэдры будут возникать в любых процессах гидролиза или коагуляции, протекание которых затруднено какими-либо факторами.

Таким образом, процесс гидролиза представляет собой строго упорядоченное агрегирование частиц в пространстве и во времени и в этом смысле подтверждает глобальную мировую закономерность пространственно-временного порядка любых процессов и явлений.

Коллоидные системы от живых организмов отделяет один шаг, для которого нужны сотни миллионов лет. Но если этот шаг сделан, дальнейшая борьба за ресурсы ускоряет эволюцию в тысячи раз.

7 Влияние магнитного и пульсирующего электростатического поля

Автор в 1974 году сделал открытие под названием «Влияние магнитного поля Земли и электростатических полей на кинетику коагуляции» и подал соответствующую заявку на признание открытия. Но система науки насквозь коррумпирована. Попробуйте представить в солидный журнал прекрасную научную статью. Если в авторах не будет известного имени какого-нибудь мафиози от науки, то ваша статья никогда не будет опубликована, какую бы ценность она не представляла. Официальный душитель новых идей пришлет вам рецензию (без подписи, чтобы не рисковать честью мундира), в которой будет отказано в публикации. Мне, например, трусливый могильщик открытий прямо заявил, что подавать заявку надо, когда станешь академиком. Только демократичный Интернет позволил публиковаться всем, кому не лень, и мне в том числе. Правда, при этом возникает большая свалка научного мусора, но, покопавшись в ней, всегда можно найти массу оригинальных идей и стимулов для дальнейшей работы. Влияние магнитного поля Земли. Эксперименты проводили на модельной системе в среде 0,1 М KCl на свежеприготовленной суспензии анатаза, устойчивость которой повышается после разбавления в течение суток за счет десорбции противоионов из сольватного слоя. Через 10 минут после начала коагуляции кювету подвешивали на длинной нити (17 колебаний в минуту) и приводили в колебательное движение вдоль магнитных силовых линий Земли или поперек их. После колебаний в течение 10 минут измеряли оптическую плотность суспензии, которая соответствует экспериментальной точке на фигуре 7.1. Начало оси ординат выбрано произвольно. 1- колебания вдоль поля, 2 – колебания поперек поля.

При колебаниях поперек магнитного поля Земли отчетливо проявляется ускорение процесса коагуляции. Независимо от устойчивости исходной суспензии, эффект увеличения скорости коагуляции при колебаниях кюветы поперек магнитного поля Земли остается, приблизительно, постоянным и равным 26%. Разброс экспериментальных точек связан с недостаточной точностью установки кюветы с раствором в кюветодержателе, которую каждый раз приходилось заново устанавливать.

. Эффект ускорения при применении постоянных магнитов в тех же условиях настолько значителен, что разница в оптической плотности легко обнаруживается простым глазом.

Интересно отметить, что возможно непосредственное решение вопроса: является ли причиной ускорения коагуляции поляризация двойного электрического слоя или дипольного сольватного слоя. Время релаксации двойного электрического слоя колеблется от 10^-5 до 10^-7 сек (Н.А. Измайлов. Электрохимия растворов. М., 1966, стр. 122). Время релаксации наружного сольватного слоя составляет, по моим данным, величину, порядка 1 секунды. Определено это наблюдением в оптический микроскоп. Частицы суспензии анатаза в микроскопе выглядят дифракционными колечками с интенсивным броуновским движением. В поле зрения микроскопа наблюдается множество столкновений частиц без всякого видимого взаимодействия между ними, но в редких случаях можно было видеть эффективное взаимодействие. Выглядит оно следующим образом. Взаимодействующие частицы, относительная скорость сближения которых в данный момент невелика, вдруг начинают синхронное броуновское движение, образуя как бы гантель с расстоянием между частицами порядка нескольких диаметров их дифракционных колец. Затем за время, порядка 1 секунда, частицы стягиваются и образуют устойчивый агрегат.

Следовательно, если менять направление перемещения кюветы или направление вектора магнитной индукции с частотой, промежуточной между 10^-5 сек и 1 секундой, то эффект ускорения коагуляции за счет поляризации двойного электрического слоя должен сохраниться, а за счет поляризации дипольного сольватного слоя этот эффект исчезнет. Проверка показала, что для данной системы даже при применении постоянных магнитов с частотой изменения вектора магнитной индукции, составляющей всего 6 сек^-1 эффект отсутствует. Отсюда следует, что магнитное поле ускоряет коагуляцию за счет поляризации сольватного слоя коллоидных частиц.

Влияние пульсирующего электростатического поля.

Результаты опытов по влиянию пульсирующего электростатического поля на коагуляцию суспензии двуокиси титана в 0,1 М растворе KCl приведены на фигуре 7.2.

На фигуре 7.2.: 1 – коагуляция в отсутствие поля, 2 – коагуляция в пульсирующем поле.

После коагуляции в течение 10 минут кювету помещали в чашку Петри и закрывали пластиной плексигласа. В течение следующих 10 минут коагуляция шла под действием пульсирующего электростатического поля, создаваемого трением о плексиглас бумажного фильтра. Как видно из фигуры 7.2. эффект увеличения скорости коагуляции в электростатическом поле оказался в два раза больше и составляет 52%, поэтому он хорошо фиксируется даже визуально. Такое увеличение скорости оказалось достаточным для неравновесного протекания коагуляции и, после снятия поля, обнаруживается слабый эффект пептизации в течение двух минут, т.е. наблюдается обратимая коагуляция. Пептизация может быть объяснена тем, что при снятии поля структура поверхности гидратного слоя частиц анатаза частично восстанавливается. Применение пульсирующих электростатических и магнитных полей в технологических процессах, связанных с состоянием наружного сольватного слоя коллоидных частиц может быть очень эффективным. Например, в данной системе достигается такая скорость коагуляции, которая не может быть достигнута ни при каких концентрациях KCl.

Описанный эффект в 52% вызван электростатическим полем малой величины, хотя наружное поле было достаточно сильным. Это следует из того, что внешнее поле компенсируется полем, возникающим внутри проводящей среды, каковой является суспензия анатаза с электролитом. Поэтому при постоянном внешнем электростатическом поле, внутри кюветы поле отсутствует. Экранировка этого поля происходит за время релаксации проводящей среды, которое равно /K, где K – проводимость среды,  - ее диэлектрическая проницаемость. Отсюда следует, что поле внутри кюветы отстает от наружного электростатического поля. Эффективное поле, действующее на частицы, будет пропорционально величине отставания. Таким образом, пульсирующее электростатическое поле, так же, как и магнитное, вызывает ускорение коагуляции за счет поляризации сольватного слоя коллоидных частиц.

Описанное открытие имеет огромное значение, особенно для биологии. Любой живой организм представляет собой сложную коллоидную систему. Каждая клетка организма имеет мембрану, несущую двойной электрический и сольватный слой. Все свойства мембраны, в конечном счете, определяются свойствами сольватного слоя и ионов. Открытие подводит научную базу под бесчисленные наблюдательные факты, которые ортодоксы склонны приписывать лженаучным фантазиям или мистике. Например, профессор Чижевский, который на примере большого числа фактов доказал влияние солнечной активности на многие биологические процессы на Земле, так и умер, оплеванный ортодоксами, которые обвиняли его во всех смертных грехах. Вместе с тем, сейчас власти вынуждены предупреждать население о предстоящих магнитных бурях. При любом движении поперек магнитных силовых линий Земли мы омагничиваем свою внутреннюю среду. Движущаяся вода ручьев, рек и океанских течений достаточно эффективно омагничивается и всегда содержит аквацеллы. Особенно этот эффект сказывается в высоких широтах Земли, где магнитные силовые линии сгущаются и направлены почти перпендикулярно поверхности земли. Особенно сильное влияние магнитной обработки должно сказываться на зарождении и развитии эмбрионов, где малейшие изменения условий имеют далеко идущие последствия.

8. Аппарат для разделения жидких изотопов

Удивительно, что хорошие идеи часто приходят в голову через много лет после проведения соответствующих экспериментов, когда воспроизвести или модифицировать их уже невозможно. Почему эти идеи не приходят сразу? Ответ я вижу в порочности самой системы науки. Часто приходя с работы жаловался матери:

- Мама, не дают работать.

- А ты не обращай внимания и работай.

Тогда приходилось долго объяснять, что нужно писать липовые отчеты, ездить в командировки, чтобы внедрять собственные изобретения, пьянствовать с руководством заводов, чтобы они подписали акт по которому мы «обучали персонал» и делели прочие полезные для завода дела, высосанные из пальца, заседания ученого совета, отзывы на работы конкурирующей организации, совещания и заседания и прочая чертовщина совершенно не оставляли времени для творческой научной работы. Когда я стал, наконец, свободным художником в деревне и никому ничем не обязан, тогда и началось реальное творчество. После этого лирического отступления станет понятно, почему родилась идея через 40 лет после моих занятий коллоидной химией.

Принцип работы аппарата хотя оригинален, но очень прост в исполнении и показан на фигуре 8.1 на примере одиночной ячейки разделения обычной и тяжелой воды. Элементарная ячейка разделения состоит из сосуда 1, заполненного водой. На воде плавает платформа 2. На платформе закреплена трубка 3 диаметром, примерно, 1 см и такой же высоты. Платформа имеет такой вес, что верхняя часть мениска воды в трубке почти совпадает с верхним срезом трубки. Работа устройства проиллюстрирована фигурой 8.2.

При испарении воды с верхней поверхности пленки поверхностного натяжения на нижней стороне этой пленки концентрируется тяжелая вода, т.к. ее испарение с вогнутого мениска затруднено из-за дополнительных связей с соседними молекулами. Тяжелая вода стекает вниз по внутренней поверхности пленки поверхностного натяжения и накапливается в нижней точке мениска до тех пор, пока под действием тяжести не оторвется в виде капли. Эта капля, конечно, расплывается при движении на дно сосуда, но в отсутствие значительной конвекции это явление не мешает разделению. Визуально описанный эффект незаметен, но прибор четко фиксирует периодическое изменение оптической плотности жидкости при падении «капли».

Аппарат в целом представляет прямоугольный контейнер, заполненный водой, в котором плавает платформа с многочисленными трубками. Таким образом, одновременно на дно сосуда могут одновременно падать тысячи «капель» тяжелой воды. В процессе работы платформа автоматически передвигается ко дну контейнера и немного всплывает, т.к. плотность жидкости постепенно увеличивается. При достижении платформой дна контейнера процесс разделения обычной и тяжелой воды повторяется бесчисленное число раз, что гарантирует высокую степень разделения. Аппарат работает автономно и не требует обслуживания и энергообеспечения. Для предотвращения значительной конвекции жидкости желательна теплоизоляция аппарата. Естественно, что в условиях обычного НИИ я не мог анализировать наличие тяжелой воды из-за бесчисленных преград нашей системы безопасности.

9. Теория возникновения протожизни на Земле

Эта теория относится к системам, которые еще не живые, но уже и не мертвые. Вечная проблема возникновения жизни на Земле до сих пор не решена из-за неверного методического подхода к решению этой проблемы. Ученые пытаются изготовить суперсмесь из отдельных аминокислот и надеются, что в этой смеси самопроизвольно зародится жизнь. Наверняка можно утверждать, что этого не произойдет. Решение проблемы происхождения жизни лежит через решение проблемы происхождения протожизни, являющуюся связующим звеном между живой и не живой природой.

Для возникновения протожизни нам потребуется вода с растворенным в ней небольшим количеством любой соли, создающей мизерную концентрацию катионов и анионов, коллоидные частицы (например, вулканического пепла) и внешний источник энергии (фотоны, радиоактивный распад изотопов или космические лучи). Принцип возникновения протожизни одинаков для любой «пищи», которая должна быть газом. В присутствии водорода возникнет «водородная протожизнь», в азоте – «азотная», в двуокиси серы – «серная», в аммиаке – «аммиачная» и т.п. Нас здесь будет интересовать возникновение «углеродной» протожизни на основе использования в качестве «питания» углекислого газа.

При попадании коллоидных частиц в воду на их поверхности адсорбируются потенциалоопределяющие ионы, которые придают частице электрической заряд (чаще всего отрицательный, примерно, 300 мв). Полярные молекулы воды выстраиваются вдоль силовых линий электрического поля и образуют термодинамически устойчивый сольватный слой толщиной, примерно, 300 . Напряженность электрического поля в этом слое 10⁷ в/м (глава 5 в разделе «Коллоидные системы»), т.е. вблизи поверхности частицы он обладает свойствами твердого тела, которые по мере удаления от поверхности постепенно утрачивает. Из-за интенсивного броуновского движения мицеллы, противоионы в растворе не могут скомпенсировать электрический заряд коллоидной частицы при адсорбции на поверхности сольватного слоя, поэтому частица обладает остаточным электрокинетическим потенциалом около 30 мв.

При сближении двух отрицательно заряженных мицелл в пространство между ними затягиваются катионы, которые также образуют частицу, подобную мицелле, которую правильней называть аквацелла, т.к. она не имеет твердого ядра (фигура 1a). Таким образом, любое сближение мицелл и аквацелл генерирует образование аквацелл, т.е. последние интенсивно размножаются. Причем при сближении двух аквацелл одного знака заряда возникает новая аквацелла противоположного знака заряда. Хотя весовая концентрация аквацелл не превышает 0,01%, счетная концентрация составляет, примерно, 1 миллиард аквацелл в 1 см³ раствора.

На следующем этапе аквацеллы с противоположными зарядами образуют диполи и таким образом значительно увеличивают время существования аквацелл (фигура 1b). Точечными линиями показано направление осей диполей воды в сольватном слое.

Диполи аквацелл, содержащие различные катионы и анионы, пристраиваясь друг к другу разноименными полюсами образуют кусок трехмерной сети, который можно было бы назвать «протоклетка» (фигура 2). На фигуре линии обозначают цепочки диполей аквацелл. Таким образом протоклетка обладает еще большей прочностью, чем отдельная цепочка диполей. Она вполне может принять шарообразную форму из энергетических соображений и в этом случае станет очень похожей на живую клетку.

Здесь нужно вспомнить о катализаторах химических реакций. Катализатор будет наиболее эффективен только в том случае, если его геометрическая форма молекулы наиболее подходит для данного химического процесса. Любое искажение этой формы дезактивирует («отравляет») катализатор. Например, в ячейке, обозначенной номером 1 фигуры 2 могут сложиться наиболее подходящие условия для синтеза из углекислого газа и воды, например, молекулы глюкозы C₆H₁₂O₆. Тогда данная ячейка будет и впредь штамповать  молекулы глюкозы, которые, очевидно, будут содействовать образованию ячеек, похожих на родительскую в других местах протоклетки или других протоклетках. Поэтому ячейку-катализатор можно рассматривать, как прабабушку ДНК, а производимые посредством ее молекулы, как прадедушку ферментов.

Очевидно, что по описанной схеме работы протожизни возможно производство любых органических соединений, например, метана и углеводородов с выделением в атмосферу лишнего в этих процессах кислорода. Возможно, что запасами газа и нефти человечество обязано именно протожизни.

Любое органическое вещество при сжигании в среде кислорода в основном образует воду и углекислый газ. Поэтому с помощью катализаторов и внешних источников энергии, способных разорвать любую химическую связь возможно осуществление обратного процесса: синтеза органических соединений. Таким образом, протожизнь хотя и не является полноценной жизнью, но на молекулярном уровне обладает всеми атрибутами жизни: понижение энтропии за счет внешней энергии, размножение, конкуренция за энергетические и пищевые ресурсы, борьба за существование и эволюционный отбор. Здесь надо отметить, что и настоящая жизнь на молекулярном уровне не отличается от неживой природы. Что будет дальше, лучше спросить у Дарвина.