Если образование молекул в современной химии так или иначе объясняется, то причины образования твердых тел, на взгляд автора, неубедительны, поскольку на уровне молекул все связи уже насыщены и, за исключением "водородной связи" и электростатической связи нет достаточных энергетических возможностей образовать из молекул твердое макротело.
|
|
|
|
|
|
С точки зрения вышеизложенных типов химической связи, в реальных объектах, связи, в принципе, никогда не могут быть полностью насыщены из-за стерических факторов. Поэтому всегда есть возможность не только собрать из молекул макротело, но и у этого макротела сохраняется способность к присоединению посторонних атомов, что проявляется в его способности к сорбции, растворению, химической активности и т.п.
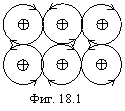
Разберем несколько примеров. На фигуре 18.1 изображена разновидность одноэлектронной связи в металлах.
Траектория случайного электрона показана стрелками. Из рисунка видно, почему металлы допускают большие пластические деформации. Подобная связь осуществляется в металле одновременно многими электронами в самых разных направлениях.
|
|
|
|
|
|
В подавляющем большинстве неметаллических веществ связь составляющих частиц имеет определенную направленность, поэтому они хрупкие. Можно сформулировать общее очевидное правило: чем более насыщены связи в молекуле - тем слабее связь между молекулами. Например, структура NH3 (фиг.18.2.a). В ней только одна связь не насыщена и в нормальных условиях NH3 - газ.
В H2O (фиг. 18.2.b) две связи не насыщены и в нормальных условиях H2O - жидкость. В NaCl (фиг. 18.2.c) не насыщенны уже три связи, поэтому NaCl - твердое вещество. У BeO (фиг. 18.2.d) кроме того, что не насыщены три связи еще и бериллий отдает один электрон кислороду полностью, т.е. в твердом окисле BeO кроме насыщения одноэлектронных связей действует еще и сильная электростатическая связь. Поэтому BeO образует очень прочную кристаллическую решетку в сравнении с NaCl.
|
|
|
|
|
|
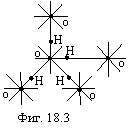
В качестве примера, на фигуре 18.3 изображена кристаллическая решетка льда в виде тетраэдра. Каждый атом кислорода окружен четырьмя атомами водорода, два из которых расположены вблизи. Все одноэлектронные связи у кислорода и водорода в этом случае насыщены.
|
|
|
|
|
|
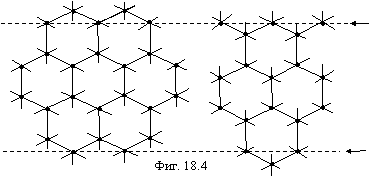
Следуя сложившейся традиции, рассмотрим в заключение этого раздела структуры алмаза и графита. Поскольку у атома углерода имеется в торе четыре электрона, то, соединяя каждый атом с четырьмя соседями в тетраэдрическую структуру с полностью насыщенными связями (это будет двухэлектронная связь), получим структуру алмаза, где каждый атом углерода обладает 8 электронами. Если осуществляется не двухэлектронная, а одноэлектронная связь между атомами углерода, то образуется плоская гексагональная решетка, в которой половина атомов углерода имеет 5 электронов, а другая половина - 6, как показано на фигуре 18.4.
Структура графита получается наложением плоскостей друг на друга (вдоль пунктирных линий). При этом атомы углерода, имеющие по 6 электронов, не образуют связи, а атомы, имеющие по 5 электронов, оказываются друг против друга и образуют одноэлектронную связь. Таким образом, в решетке графита все атомы углерода имеют по 6 электронов, соответственно, прочность ее значительно ниже, чем у алмаза.
Здесь описаны, за недостатком места, только принципиальные основы новых взглядов на химическую связь и приведены примеры небольшого числа соединений. Читатель может поверить автору на слово, что он проанализировал большое число различных химических соединений и не нашел ничего, что противоречит вышеизложенному, хотя химия имеет дело с огромным разнообразием соединений.
18.1. О «поверхностном газе» жидкостей и твердых тел
Понятие о поверхностном газе жидкостей и твердых тел.
Оно помогает объяснить многие их свойства и дать количественную теорию этих свойств. Атомы или молекулы, из которых состоит твердое тело или жидкость способны выскочить из объема на поверхность и достаточно свободно передвигаться по ней, перепрыгивая из одной потенциальной ямы в другую, поскольку энергетический барьер для таких прыжков небольшой. Если энергия активации перехода в поверхностный газ достаточно большая, то концентрация молекул в поверхностном газе, соответственно, мала и его можно считать идеальным двумерным газом.
Концентрация частиц в поверхностном газе.
Скорость перехода частиц в поверхностный газ:
(18.1.1.),
где: C0 – поверхностная концентрация частиц вещества, 1/см2,
C – концентрация частиц в поверхностном газе.
Скорость конденсации из поверхностного газа в объем вещества:
(18.1.2.).
Равновесие устанавливается быстро, т.к. процесс конденсации не имеет энергии активации:
(18.1.3.).
(18.1.1.) и (18.1.2.) подставим в (18.1.3.) и найдем:
(18.1.4.).
По Аррениусу:
, 
, т.к. E2=0
(18.1.5.),
где: E1 и E2 – энергии активации, соответственно, перехода частицы в поверхностный газ и конденсации в объем вещества, эрг/моль.
(18.1.5.) подставим в (18.1.4.) и при 
(частицы
одни и те же), найдем:
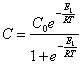(18.1.6.).
При E1>>RT (18.1.6.) примет вид:
(18.1.7.).
Чем ближе к состоянию расплавления твердого тела или кипения жидкости, тем ниже E1 и при E1=0 (18.1.6) примет вид: C=C0/2, что очевидно.
Энергия активации переноса частицы в поверхностный газ будет равна сумме:
(18.1.8.),
где: Q – энергия, необходимая для разрыва связей с атомами объема вещества при данной температуре, кал/моль,
F – удельная свободная поверхностная энергия.
QT найдем из следующих соображений. Чтобы разорвать связи в жидкости при данной температуре, ее нужно нагреть до температуры кипения и испарить, затем охладить пар до исходной температуры, но без конденсации. Чтобы разорвать связи в твердом теле, нужно его нагреть до Tпл и расплавить. В образовавшейся жидкости связи настолько ослаблены, что ими можно пренебречь в первом приближении и молекулы или атомы считать практически свободными. Образовавшуюся жидкость надо охладить до исходной температуры без кристаллизации в твердое тело. При этом следует заметить, что автоматически учитывается и удельная свободная поверхностная энергия. Поэтому в первом приближении (без охлаждения газа или жидкости от температуры фазового перехода до исходной температуры). Для концентрации частиц в поверхностном газе такое упрощение допустимо:
кал/моль
(18.1.9.),
где: cp – теплоемкость, кал/г×град,
M – молекулярный вес, г,
T=Tф-T, где Tф – температура фазового
превращения, град,
0 – удельная теплота
плавления или испарения, кал/моль.
Формально, мы можем приписать энергию по (18.1.9.) одному атому. При этом учтем, что при выходе в поверхностный газ атом обладает одной степенью свободы, поэтому достаточно трети этой энергии, она и будет энергией активации:
(18.1.10.).
Подставив (18.1.10.) в (18.1.7.), найдем:
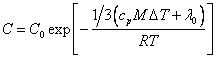(18.1.11.).
Выражение (18.1.11.) справедливо вдали от температуры кипения или плавления, вблизи их нужно (18.1.10.) подставить в (18.1.6.):
(18.1.12.).
Легко показать, что:
(18.1.13.),
где: C0 – поверхностная концентрация частиц вещества, см-2,
d – плотность вещества, г/см3,
N0 – число Авогадро, моль-1,
M – молекулярный вес, г.
Поверхностное натяжение.
Энергия по уравнению (18.1.10.), приходящаяся на одну частицу:
(18.1.14.).
Перемножив число частиц по (18.1.13.), на энергию, приходящуюся на одну частицу по (18.1.14.), получим:
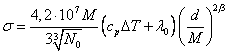эрг/см2
(18.1.15.).
Выражение (18.1.15.) можно трактовать, как поверхностное натяжение без
учета поверхностного газа, который не вносит вклад в 
.
В таблице 18.1.1. представлены вычисленные и экспериментальные значения поверхностного натяжения для воды и ртути при 200С в эрг/см2.
Таблица 18.1.1.
|
Вещество
|
Вычислено по (18.1.15.)
|
Табличное значение
|
|
Вода |
70 |
72,75 |
|
Ртуть |
444 |
472 |
Для летучих жидкостей пренебрегать концентрацией атомов в поверхностном газе нельзя, т.к. при изменении поверхности эти атомы не оказывают влияния, поэтому результаты расчета по (18.1.15.) оказываются завышенными. Например, для этилового спирта вычисленное значение по (18.1.15.) 56,7 эрг/см2, а экспериментальное 22,8 эрг/см2. Очевидно, что эффективная концентрация частиц на поверхности, влияющая на поверхностное натяжение, будет:
(18.1.16.),
где C определяется выражением (18.1.12.). Если его подставить в (18.1.16) и умножить на энергию, приходящуюся на одну частицу, получим:
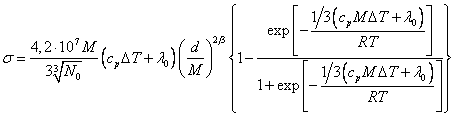(18.1.17.).
Известное эмпирическое выражение, пригодное для многих жидкостей, выглядит так:
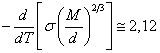(18.1.18.).
Если дифференцировать по температуре (18.1.15.), как более простое, в сравнении с уточненным (18.1.17), получим такой же результат:
(18.1.19.).
Теплота испарения.
Энергию, необходимую для нагрева и испарения жидкости при температуре кипения найдем по известному соотношению:
(18.1.20.),
где: 
- средняя теплоемкость жидкости,
кал/моль×град,
Tж = Tкип – T,
исп – теплота испарения
при температуре кипения, кал/моль.
Аналогично для твердого тела:
(18.1.21.),
где: 
- средняя теплоемкость твердого тела,
кал/моль×град,
T1 = Tпл – T,
пл
– теплота плавления, кал/моль,
T2 = Tкип – Tпл.
Образовавшийся газ в результате процессов (18.1.20.) и (18.1.21.) имеет избыточную энергию:
(18.1.22.),
где: 
- средняя теплоемкость газа, кал/моль,
T = Tкип – T.
Если мы учтем это обстоятельство, то в результате получим для жидкостей:
(18.1.23.)
и для твердых тел:
(18.1.24.).
Поскольку теплоемкость тел зависит от температуры, мы получили приблизительное значение теплоты испарения. Чтобы иметь точное значение, надо знать экспериментальную величину затраченной интегральной теплоты.
Сравнение вычисленных по (18.1.23.) и (18.1.24.) и экспериментальных значений теплоты испарения разных веществ при разных температурах представлено в таблице 18.1.2.
Таблица 18.1.2.
|
Вещество |
Температура, 0С |
|
|
|
CdCl2 |
568 |
41,2 |
41,1 |
|
Cs |
28,7 |
18,82 |
19,9 |
|
FeCl3 |
304 |
16,5 |
16,6 |
|
H2O |
0 |
10,77 |
10,80 |
|
H2O |
25 |
10,51 |
10,53 |
|
H2Se |
-65,7 |
5,34 |
5,61 |
|
Hg |
-38,9 |
15,20 |
15,73 |
|
Hg |
25 |
14,54 |
15,43 |
|
KBr |
735 |
48,9 |
51,1 |
табличное
Давление насыщенного пара.
Очевидно, что значения, определяемые по уравнениям (18.1.23.) и (18.1.24.)
будут энергиями активации перехода частиц из поверхностного газа в газовую
фазу, соответственно для жидкости и твердого тела. Поэтому устроим еще одну
проверку справедливости уравнения (18.1.23.) на предмет дальнейшего
использования. Используем табличные данные для воды (теплота испарения при 1000С
9717 кал/моль, 
=9,971 кал/моль×град,
1 кал = 4,1858 дж). Результаты сравнения расчета по (18.1.23.) с табличными
данными при разных температурах представлены в таблице 18.1.3.
Таблица 18.1.3.
|
Температура, 0С |
Экспериментальная теплота испарения, дж/г |
Вычисленная теплота испарения, дж/г |
|
0 |
2501 |
2492 |
|
5 |
2489 |
2480 |
|
10 |
2477 |
2469 |
|
15 |
2465 |
2457 |
|
20 |
2454 |
2446 |
|
25 |
2442 |
2434 |
|
30 |
2430 |
2423 |
|
40 |
2406 |
2399 |
|
50 |
2382 |
2376 |
|
100 |
2257 |
2260 |
Данные таблицы 18.1.3. показывают, что уравнение (18.1.23.) приемлемо для ориентировочных расчетов.
Будем считать, что поверхностный газ является идеальным двумерным газом и подчиняется известному уравнению газового состояния:
(18.1.25.),
Число молей в поверхностном газе:
(18.1.26).
В (18.1.25.) подставим (18.1.26.) и значение газовой постоянной R:
(18.1.27.),
где давление выражено в атмосферах. Если в (18.1.27.) подставим (18.1.12.) и (18.1.13.) с учетом (18.1.23.), то получим окончательно:
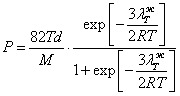(18.1.28.).
Для твердых тел надо учесть не (18.1.23.), а (18.1.24.).