Строение атома является следствием стремления любой системы к минимуму потенциальной энергии, а не каких-либо правил отбора или определенного набора квантовых чисел. Стремление к минимуму потенциальной энергии является достаточным, исчерпывающим для описания атомов.
“В основе оперирования представлением о характеристике состояния электрона в атоме с помощью четырех квантовых чисел (n, l, ml, ms) лежит принцип запрета (или принцип исключения), сформулированный В. Паули. Согласно принципу Паули, в атоме не может быть двух электронов, состояние которых описывалось бы совершенно одинаковым сочетанием значений названных выше четырех квантовых чисел; хотя бы одно из них должно принимать различные значения”. “О систематике частиц”, “Атомиздат”, М., 1969, стр.12. Казалось бы, официальной физике можно кричать: “Ура!” и изобразить электронные конфигурации всех атомов. Ан нет! Ничего не получается, пока не применишь правило Ф. Гунда: “... электроны в пределах данной подоболочки стремятся расположиться таким образом, чтобы величина их суммарного спина была максимальной...” (там же, стр.14). Чувствуете противоречие с принципом Паули? Один требует разного состояния электронов, другой - одинакового. “На основе принципа Паули в сочетании с правилом Гунда можно дать схему (так называемая, идеальная схема), характеризующую распределение электронов соответственно значениям квантовых чисел” (там же, стр.14). Ну, теперь то, можно кричать “ура”? Конечно, нет! Следующая цитата весьма характерна для ортодоксального мышления. “Тем не менее, широко распространилась тенденция считать идеальную схему именно нормальной, в то время как реальная периодическая система рассматривалась в качестве аномальной, как частный случай аномального, незакономерного проявления периодичности. Это противоречие, конечно, тормозило дальнейшее развитие теории периодической системы. Для того чтобы преодолеть это противоречие, необходимо было отказаться не только от представления о доминирующей роли главного квантового числа n (вот тебе, бабушка, и главное квантовое число! - В.К.) в определении последовательности формирования электронных конфигураций многоэлектронных атомов, но и от того, что вообще энергетическое состояние электрона в многоэлектронном атоме всегда
|
|
|
|
|
|
преимущественно определяется главным квантовым числом” (там же, стр.21).
Впервые от доминирующей роли главного квантового числа отказался В.М.
Клечковский, сформулировав (n+l) - правило: “Эта закономерность наиболее
отчетливо вскрывается, если группировку квантовых уровней электронов в атоме
подчинить принципу, основанному на объединении в одну группу уровней с
одинаковым значением суммы главного (n) и орбитального (l) квантовых
чисел” (там же, стр.22). Вся эта канитель с наслоением правил друг на друга
имеет, в конечном итоге, пессимистический финал: “Мы должны, прежде всего,
отметить, что реальная схема формирования электронных конфигураций атомов в
некоторых случаях оказывается не столь строго последовательной, как это должно
было бы вытекать из (n+l)-правила. Наблюдается три основных типа
расхождений” - далее они перечисляются (там же, стр.40).
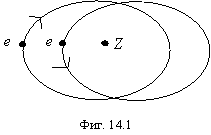
Рассмотрим двухэлектронный атом, изображенный на фигуре 14.1. Можно показать, что орбиты электронов не являются эллиптическими, а только эллипсовидными, однако, для простоты расчетов можно принять их эллиптическими, заменяя реальную орбиту эквивалентным эллипсом. При этом мы, естественно, уже не можем рассчитывать на строгое количественное совпадение с экспериментальными данными, но таковое в принципе невозможно при взаимодействии многих тел. На фигуре механические и магнитные моменты электронов изображены антипараллельными, т.к. только при таком положении система будет иметь минимальную потенциальную энергию. Взаимодействие магнитных моментов учитывать здесь не будем. В первом приближении, без них результаты получатся неплохими в отличие от квантовой механики, которую спасает только рассмотрение этого взаимодействия. “Тождественность одинаковых частиц приводит в квантовой механике к специфическому взаимодействию между ними, называемому обменным взаимодействием. ... Обменная энергия не имеет классического аналога. ... Величины, называемые иногда обменной плотностью, нельзя истолковать как обычные плотности заряда: они могут быть и комплексными. ... Обменная энергия является электростатической - она пропорциональна квадрату заряда электрона. ... Чем больше степень перекрытия волновых функций (“электронных облаков”), тем больше обменная энергия. ... Благодаря обменной энергии в одной и той же системе могут существовать как силы притяжения, так и силы отталкивания”. “Физика микромира”, “Советская энциклопедия”, М., 1980, стр.42-43. Несмотря на то, что в этом вопросе физики основательно натемнили, фактически существует только два варианта интерпретации обменного взаимодействия: или это взаимное притяжение антипараллельных магнитных моментов электронов (или отталкивание параллельных), или надо вводить новый вид взаимодействия. По многим причинам оба эти варианта совершенно не подходят для квантовой механики, поэтому у обменного взаимодействия отсутствует физический смысл.
Положение электронов, соответствующих фиг. 14.1, один в перицентре орбиты, другой - в апоцентре. Общая энергия связи обоих электронов Eсв1,2 аналогично выражению (13.1), составит выражение:
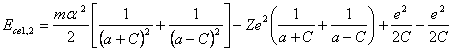 (14.1).
(14.1).
В (14.1) последние два члена взаимно уничтожаются, т.к. энергия
взаимодействия электронов между собой заставляет электрон в перицентре
"притягиваться" к ядру, а электрон в апоцентре -
"отталкиваться". Заменяя в (14.1) C через эксцентриситет ![]() , после
преобразований найдем:
, после
преобразований найдем:
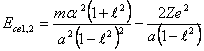 (14.2).
(14.2).
Дифференцируя (14.2) по ![]() и приравнивая производную нулю, найдем
большую полуось стационарной орбиты:
и приравнивая производную нулю, найдем
большую полуось стационарной орбиты:
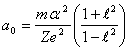 (14.3).
(14.3).
Подставив (14.3) в (14.2), найдем энергию связи в основном состоянии:
![]() (14.4).
(14.4).
Очевидно, что ![]() является суммой первого
является суммой первого ![]() и
второго
и
второго ![]() потенциалов ионизации гелиоподобного
атома.
потенциалов ионизации гелиоподобного
атома. ![]() мы уже знаем для водородоподобных
атомов, поэтому:
мы уже знаем для водородоподобных
атомов, поэтому:
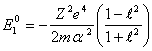 (14.5).
(14.5).
Из (14.5) или (14.4) по экспериментальным потенциалам ионизации легко найти эксцентриситеты стационарных орбит (цифра при e обозначает заряд ядра гелиоподобного атома): e2 = 0,6143, e3 = 0,4859, e4 = 0,4141, e5 = 0,3667, e6 = 0,3325, e7 = 0,3062, e8 = 0,2853, e9 = 0,2678, e10 = 0,2534, e11 = 0,2408.
В расчете на один электрон, аналогично (13.4), запишем:
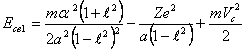 (14.6),
(14.6),
и обозначая:
![]() (14.7),
(14.7),
из (14.6) с учетом (14.7) найдем Vc, продифференцируем ее по ![]() , убедимся, что максимальное значение
, убедимся, что максимальное значение ![]() соответствует
соответствует
![]() и
найдем:
и
найдем:
![]() (14.8).
(14.8).
Учитывая, что ![]() и
и ![]() при излучении
фотонов, сравнивая с (14.8), найдем:
при излучении
фотонов, сравнивая с (14.8), найдем:
![]() (14.9).
(14.9).
Подставив (14.9) в (14.7), получим:
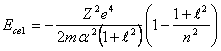 (14.10),
(14.10),
тогда энергия фотона:
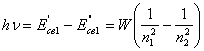 (14.11).
(14.11).
Формула (14.11) справедлива для любого электрона в любом атоме, если W считать функцией n1 и n2. Это уравнение можно получить и из более общих соображений. Излучение фотона для атомов, содержащих больше одного электрона, хотя и будет определяться переходом данного электрона на более низкую орбиту, но величина энергии фотона будет зависеть уже не только от разницы энергии связи данного электрона, но и всех остальных электронов, поскольку происходит автоматическая перестройка структуры всего атома. Кроме того, одновременно меняется и энергия взаимодействия электронов между собой. Поэтому для любого электрона в любом атоме:
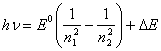 (14.12),
(14.12),
где ![]() E - некоторая функция от n1 и
n2, а E0 -
энергия связи электрона в основном состоянии. Приравнивая (14.12) любой
известной полуэмпирической или совсем эмпирической зависимости, удачно
подходящей для описания спектров, мы всегда найдем
E - некоторая функция от n1 и
n2, а E0 -
энергия связи электрона в основном состоянии. Приравнивая (14.12) любой
известной полуэмпирической или совсем эмпирической зависимости, удачно
подходящей для описания спектров, мы всегда найдем ![]() E в явном виде. Известные зависимости обычно допускают
фактически не целочисленные значения n1 и
n2.
Например, частоты линий в спектрах щелочных элементов определяются формулой:
E в явном виде. Известные зависимости обычно допускают
фактически не целочисленные значения n1 и
n2.
Например, частоты линий в спектрах щелочных элементов определяются формулой:
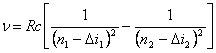 ,
,
где ![]() i - поправка
(так называемый квантовый дефект). Для каждого элемента значения поправок
различны, кроме того, они различны и для одного и того же элемента в зависимости
от значения орбитального квантового числа l. R - постоянная Ридберга. Г.Е. Пустовалов “Атомная и
ядерная физика”, Издательство Московского Университета, 1968, стр.118.
i - поправка
(так называемый квантовый дефект). Для каждого элемента значения поправок
различны, кроме того, они различны и для одного и того же элемента в зависимости
от значения орбитального квантового числа l. R - постоянная Ридберга. Г.Е. Пустовалов “Атомная и
ядерная физика”, Издательство Московского Университета, 1968, стр.118.
Мы не будем так легко, как это делает современная физика, изменять идее
квантованности при первых же расхождениях с опытными данными, хотя у
официальной физики больше поводов сохранять верность, т.к. она считает
квантованность изначальной причиной поведения электрона в атоме. Альтернативная
физика считает появление квантованности неизбежным разрешением конфликта между
стремлением электрона к минимуму потенциальной энергии и невозможностью
излучения нецелого фотона. Не трогая целочисленности n1 и n2, будем
считать W функцией n1 и
n2,
тогда из (14.12) получим (14.11). W при n2![]()
![]() и n1=1 численно
равна энергии связи электрона в невозбужденном состоянии (E0),
вернее, потенциалу ионизации при удалении данного электрона и зависит от
степени возбуждения электрона (положения его орбиты).
и n1=1 численно
равна энергии связи электрона в невозбужденном состоянии (E0),
вернее, потенциалу ионизации при удалении данного электрона и зависит от
степени возбуждения электрона (положения его орбиты).
Уравнение (14.11), по мнению автора, предпочтительней любых других полуэмпирических выражений по следующим обстоятельствам:
1. Оно имеет предельно ясный физический смысл.
2. Целочисленность n1 и n2 позволяет легко интерпретировать спектральные линии.
3. Поскольку изменение энергии связи данного электрона вносит решающий вклад в энергию излучаемого фотона, то значение W всегда близко к значению E0.
В связи с изложенным, есть смысл составить таблицу значений ![]() ,
которая очень удобна для анализа спектров.
,
которая очень удобна для анализа спектров.
Таблица 14.1.
|
n2 n1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
1 |
0 |
0,750 |
0,889 |
0,938 |
0,960 |
0,972 |
0,980 |
0,984 |
0,988 |
0,990 |
1,000 |
|
2 |
|
0 |
0,139 |
0,188 |
0,210 |
0,222 |
0,230 |
0,234 |
0.238 |
0,240 |
0,250 |
|
3 |
|
|
0 |
0,049 |
0,071 |
0,083 |
0,091 |
0,095 |
0,099 |
0,101 |
0,111 |
|
4 |
|
|
|
0 |
0,022 |
0,034 |
0,042 |
0,046 |
0,050 |
0,052 |
0,062 |
|
5 |
|
|
|
|
0 |
0,012 |
0,020 |
0,024 |
0,028 |
0,030 |
0,040 |
|
6 |
|
|
|
|
|
0 |
0,008 |
0,012 |
0,016 |
0,018 |
0,028 |
|
7 |
|
|
|
|
|
|
0 |
0,004 |
0,008 |
0,010 |
0,020 |
|
8 |
|
|
|
|
|
|
|
0 |
0,004 |
0,006 |
0,016 |
|
9 |
|
|
|
|
|
|
|
|
0 |
0,002 |
0,012 |
|
10 |
|
|
|
|
|
|
|
|
|
0 |
0,010 |
Анализ спектров удобно проводить по следующей схеме: а). Выявляем
энергию связи электрона на стационарных орбитах данного атома. б). Любую спектральную
линию этого атома переводим в энергию фотона, выраженную в электрон-вольтах по
формуле: 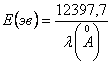 и из
формулы (14.11) находим W, пользуясь таблицей значений
и из
формулы (14.11) находим W, пользуясь таблицей значений ![]() .
Значение
.
Значение ![]() надо выбрать из таблицы таким образом,
чтобы W было наиболее близко к значению какой-либо энергии связи
электрона на стационарной орбите. Таким образом, для каждой линии спектра
найдем W и значения n1 и n2.
надо выбрать из таблицы таким образом,
чтобы W было наиболее близко к значению какой-либо энергии связи
электрона на стационарной орбите. Таким образом, для каждой линии спектра
найдем W и значения n1 и n2.
Применим эту схему для анализа спектральных линий гелия. По формуле
(14.4) на один электрон в стационарном состоянии приходится энергия связи 39,5
эв. Для того чтобы получить линии спектра при E0=39,5 эв, необходимо
совершенно одинаковое и одновременное возбуждение обеих электронов гелия, что
очень маловероятно. Другое энергетическое состояние атома гелия, при котором
энергия связи первого электрона составляет 24,6 эв (первый потенциал
ионизации), а второго 54,4 эв (второй потенциал ионизации) энергетически
равносильно энергии связи обоих электронов по 39,5 эв, т.к. в сумме энергия
одинакова: 79 эв. Мы имели бы совершенно иной мир, если бы магнитное
взаимодействие орбитальных электронных токов не стабилизировало бы электроны на
орбите 39,5 эв. Тогда бы электроны предпочли занять разные орбиты: 24,6 эв и
54,4 эв. Поэтому возбуждение любого электрона провоцирует подобную перестройку
орбит и в спектре гелия мы должны фиксировать соответствующие серии линий.
Кроме того, в любом достаточно сильно возбужденном атоме (при малом n1),
мы должны наблюдать линии, соответствующие W![]() 13,6 эв, т.к. с точки зрения
электрона на высокой орбите, атом представляется водородоподобным. Поскольку
при удалении электрона от ядра происходит перестройка остальных электронных
орбит в структуру, соответствующую атому, занимающему предыдущее положение в
таблице элементов Менделеева (при ионизации цинка образуется медьподобная
структура, при ионизации меди - никельподобная и т.д.), то в спектрах элементов
с последовательно увеличивающимся зарядом ядра повторяется картина линий
предыдущего элемента с соответствующим смещением в коротковолновую область и
расширением промежутка между линиями. В таблице 14.2 приведены данные
расшифровки некоторых линий в спектре гелия.
13,6 эв, т.к. с точки зрения
электрона на высокой орбите, атом представляется водородоподобным. Поскольку
при удалении электрона от ядра происходит перестройка остальных электронных
орбит в структуру, соответствующую атому, занимающему предыдущее положение в
таблице элементов Менделеева (при ионизации цинка образуется медьподобная
структура, при ионизации меди - никельподобная и т.д.), то в спектрах элементов
с последовательно увеличивающимся зарядом ядра повторяется картина линий
предыдущего элемента с соответствующим смещением в коротковолновую область и
расширением промежутка между линиями. В таблице 14.2 приведены данные
расшифровки некоторых линий в спектре гелия.
Таблица 14.2.
|
n1 |
n2 |
Длина волны фотона, (A0) |
W,(эв) |
|
1 |
3 |
584,33 |
23,87 |
|
3 |
5 |
7065,20 |
24,68 |
|
3 |
6 |
5875,63 |
25,32 |
|
3 |
7 |
5769,60 |
23,69 |
|
3 |
10 |
5015,678 |
24,47 |
|
3 |
4 |
4685,75 |
54,00 |
|
4 |
7 |
5460,73 |
53,94 |
|
4 |
8 |
4916,00 |
53,81 |
|
4 |
8 |
4960,32 |
54,33 |
|
2 |
3 |
6678,149 |
13,36 |
|
2 |
4 |
4916,00 |
13,45 |
|
2 |
4 |
4960,32 |
13,29 |
|
2 |
6 |
4120,82 |
13,54 |
|
2 |
7 |
4026,192 |
13,41 |
|
2 |
8 |
3888,645 |
13,60 |
|
|
|
|
|
|
Как и следовало ожидать, значения W близки к значениям 54,4 эв, 24,6 эв и 13,6 эв.
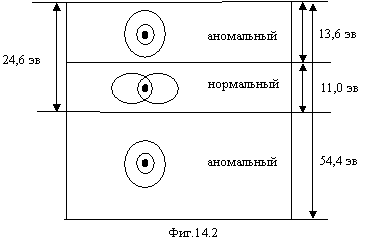
Таблица 14.2 показывает, что атом гелия имеет три системы спектральных линий. Фигура 14.2 объясняет систему спектральных линий нормального атома гелия с Е0=24,6 эв. Системы спектральных линий с Е0=54,4 эв и 13,6 эв относятся к аномальному атому гелия. Он образуется следующим образом. Для разрыва магнитного притяжения электронов необходима энергия 11 эв (см. формулу 16.5 в главе 16). При получении этой энергии электроны уже не могут занимать положение, соответствующее фигуре 14.2 и образуют следующую конфигурацию: наружный электрон занимает квазистационарную орбиту с энергией связи 24,6–11=13,6 эв, поэтому его энергетические уровни практически соответствуют уровням атома водорода. Внутренний электрон занимает орбиту с энергией связи 54,4 эв, поэтому его энергетические уровни соответствуют водородоподобному атому с зарядом ядра +2. Таким образом, аномальный гелий хотя и метастабилен, но достаточно устойчив. Это надо учитывать, чтобы спектральные линии нейтрального гелия не спутать с линиями нейтрального водорода или однократно ионизированного гелия. Изложенная ситуация изображена схематично на фигуре 14.2 где изображены области существования нормального и аномального гелия. Наружный электрон движется по радиусу первой орбиты Бора, а внутренний по орбите с радиусом в два раза меньшим.
14.1. Эффективный заряд и влияние магнитного орбитального взаимодействия
Поскольку энергия связи электрона в атоме пропорциональна квадрату эффективного заряда ядра, то можно записать отношение:
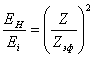 (14.1.1),
(14.1.1),
откуда:
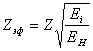 (14.1.2),
(14.1.2),
где Ei – энергия связи (ионизации) электрона в i-том атоме или ионе с зарядом Z с определенного энергетического уровня, EH – энергия связи (ионизации) водородоподобного атома с зарядом Z с энергетического уровня того же номера.
Для лития в основном состоянии: Ei=5,39 эв, EH=13,6 эв, Zэф=0,629. Уменьшение заряда обусловлено близостью внутренних электронов к наружному. Поскольку сила притяжения к ядру пропорциональна заряду в первой степени, а сила отталкивания от внутренних электронов обратно пропорциональна квадрату расстояния, то они сильно уменьшают энергию ионизации.
Для Li+ в основном состоянии: Ei=75,7 эв, EH=54,1 эв, Zэф=1,182. В этом случае магнитное орбитальное притяжение двух оставшихся в литии электронов приводит к увеличению энергии ионизации (эффективного заряда). Таким образом, наличие внутренних электронов приводит к уменьшению эффективного заряда, а орбитальное магнитное взаимодействие данного электрона с другими электронами атома производит такое же действие как увеличение эффективного заряда.
Энергию связи электрона на любом уровне водородоподобного атома ЕН мы уже знаем (формула 13.17). Очевидно, что аналогичная формула для любого электрона в любом атоме будет отличаться только значением эффективного заряда Zэф вместо Z. Разница этих энергий связи:
![]() E=EH
–Ei
(14.1.3),
E=EH
–Ei
(14.1.3),
Из (14.1.3) найдем Еi:
![]() (14.1.4),
(14.1.4),
где Е0 – энергия ионизации атома водорода.
Из (14.1.4) видно, что эффективный заряд ядра меняется не только в зависимости от степени ионизации, но и от энергетического уровня, на котором находится электрон, т.е. от расстояния до внутренних электронов и формы орбиты.
Энергия фотона, который излучается при переходе на нижние уровни, равна разнице энергии связи на конечном и исходном уровне. Для этого случая формула (14.1.4) примет вид:
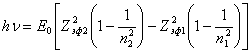 (14.1.5).
(14.1.5).
Вблизи основного состояния уровни энергии расположены густо, поэтому эффективный заряд остается практически одинаковым. Для этого случая (14.1.5) упрощается:
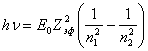 (14.1.6).
(14.1.6).
Естественно, что формула (14.1.5) будет давать точные значения энергии излученных фотонов, но практически пользоваться ей – это обманывать самого себя, т.к. Zэф зависит от n и пока может быть найден только из экспериментальных данных. Полезней пользоваться формулой (14.1.2), чтобы по эффективному заряду судить о строении атома. Тогда можно построить теорию для аналитического определения эффективного заряда и формула (14.1.5) станет очень полезной.
Здесь необходимо отметить еще одно принципиальное отличие во взглядах на излучение фотонов атомом в современной и представленной читателю альтернативной физике. Современная физика считает, что причиной излучения является переход электрона на другую орбиту (вернее, в другое состояние, т.к. она не признает ни орбит, ни электрона, как целостной частицы в атоме), а излучение фотона является следствием такого перехода. Очевидно, что, в этом случае, причина перехода электрона в новое состояние остается неясной, кроме того, сам фотон оказывается в затруднительном положении, поскольку должен "помнить" исходное состояние электрона, которое может быть любым. Квантовая механика в качестве решений уравнения Шредингера получает не метастабильные, а устойчивые “возбужденные” состояния электронов в атоме, поэтому вынуждена объяснять неустойчивость таких состояний взаимодействием электрона с виртуальными частицами, рождающимися в вакууме.
Новая физика считает, что атом излучает фотон по причине стремления к минимуму потенциальной энергии, причем он может излучить любой фотон в пределах, разрешаемых центробежной скоростью электрона и условием уменьшения этой скорости в целое число раз, а новая орбита с энергией связи более близкой к дну потенциальной ямы будет следствием излучения. Положа руку на сердце, следует признать, что современной физике вообще не с руки заниматься выяснением причинно-следственной связи излучения фотона и состояния электрона, поскольку при любом раскладе фотон должен "предвидеть" конечное состояние электрона или "помнить" начальное. Как он это умудряется делать - официальная наука объяснить не в состоянии и не собирается это делать, т.к. квантовая механика - статистическая теория, отвергающая детерминизм в микромире (см. соотношения неопределенностей Гейзенберга).
Несколько слов необходимо сказать о тонкой структуре спектральных линий, которую автор связывает (в частности) с прецессионными движениями. Причиной прецессии орбиты электрона является наклон оси вращения электрона к плоскости орбиты, что, в свою очередь, является следствием движения свободного электрона по винтовой линии. Траектория электрона в плоскости, перпендикулярной оси прецессии аналогична фигурам Лиссажу и зависит от соотношения частот прецессии и обращения электрона вокруг ядра. Кроме прецессии орбиты электрона, одновременно происходит и прецессия оси вращения самого электрона (орбит составляющих его нейтрино, см. главу об "элементарных" частицах) и прецессия осей вращения нейтрино из которых состоит электрон. Прецессионные движения расщепляют уровни энергии связи электрона с ядром на ряд подуровней, поскольку механизм их образования имеет много схожих черт с механизмом образования устойчивых орбит электрона в атоме (разрешенных орбит). Имеются еще причины, приводящие к расщеплению уровней энергии, на которых останавливаться не будем, например, одной из причин является внутреннее строение электрона, который сам очень напоминает атом, в котором функцию электронов выполняют нейтрино. Здесь только отметим, что официальная физика одной из причин тонкой структуры спектральных линий считает релятивистское увеличение массы электрона в зависимости от скорости. Но это увеличение происходит не квантованно, а плавно, следовательно, никак не может создать дополнительные квантованные уровни энергии, проявляющиеся в виде тесно расположенных спектральных линий. Кроме того, в главе 5.2.2 показано, что релятивистских электронов не содержится в любых мыслимых атомах.
“Тонкая структура спектральных линий является квантоворелятивистским эффектом. Она объясняется результатом действия двух факторов: 1) взаимодействием собственного магнитного момента электрона с магнитным моментом орбитального движения электрона; 2) релятивистской зависимостью массы электрона от скорости”. Н.И. Карякин и др. “Краткий справочник по физике”, “Высшая школа”, М., 1962, стр.350.