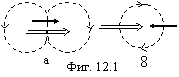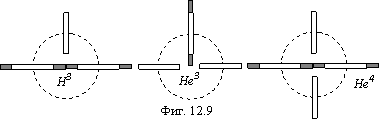Если составляющие
"элементарных" частиц движутся упорядочено и
устойчивость определяется, в основном, динамической устойчивостью
гравидинамических систем, при этом релятивистский прирост массы поровну
распределяется на рост измеряемой массы и энергию связи, то в ядрах нужно вести
речь о статической устойчивости гравидинамических систем, т.к. в них частицы
относительно неподвижны в том смысле, как мы говорим о
"неподвижности" атомов в узлах кристаллической решетки твердого тела.
При этом наблюдается дефект массы, при котором часть уходит на энергию связи, а
“часть массы исходных частиц передается в той или иной форме окружающей среде”
(Н.И. Карякин и др., Краткий справочник по физике, “Высшая школа”, М., 1962,
стр. 423). Действительно, если бы нуклоны осуществляли гравидинамическую связь
при своем движении, то мы наблюдали бы не дефект массы при образовании ядра, а
приращение ее, эквивалентное энергии связи (примерно 8 Мэв). Поэтому связь
нуклонов в ядре осуществляется за счет гравидинамического поля самих нуклонов
аналогично тому, как взаимодействовали бы магнитные поля кольцевых рамок с
электрическим током. Эта аналогия делает ясной картину статического взаимодействия
нуклонов, хотя современной ядерной физике слепая вера в квантовые законы мешает
внести ясность в этот вопрос. Современная физика считает, что нуклоны в ядре
удерживаются за счет обмена ![]() -мезонами,
масса которых, примерно, в семь раз меньше массы нуклона. При этом вместо
дефекта массы при образовании ядра мы должны наблюдать увеличение его массы за
счет пионов, чего на самом деле нет.
-мезонами,
масса которых, примерно, в семь раз меньше массы нуклона. При этом вместо
дефекта массы при образовании ядра мы должны наблюдать увеличение его массы за
счет пионов, чего на самом деле нет.
“Общий характер движения нуклонов известен - это квантовые законы. Математического выражения для ядерных сил не получено, поэтому физики вынуждены строить различные модели ядер для объяснения тех или других процессов. Существуют различные модели ядер, хорошо объясняющие отдельные процессы, но пока еще не предложено единой модели”. Н.И. Карякин и др., Краткий справочник по физике, “Высшая школа”, М., 1962, стр. 424.
Методика все та же - подгонка под ответ: “Подбирая порядок уровней тонкой и грубой структуры, удалось объяснить магические числа, спин и магнитный момент большинства ядер”. Там же, стр.426.
“Короткодействующий характер ядерных сил и зарядовая независимость передаются потенциалом Юкавы. Однако ядерные силы обладают целым рядом других свойств, которые не передаются этим выражением. При сближении центров ядер до расстояний, меньших, чем сумма их радиусов, между ними начинают действовать мощные силы отталкивания, препятствующие их взаимному прохождению сквозь друг друга. (Поэтому представления официальной физики о возможности существования сверхядерной плотности, например, в «черных дырах» ни на чем не основаны – В.К.)
Ядерные силы обладают свойством насыщения. Они зависят от ориентации спина, имеют нецентральный характер и некоторые другие свойства. Чтобы учесть эти свойства ядерных сил, были предложены различные варианты теории ядерных сил - псевдоскалярный, векторный, псевдовекторный, тензорный. Однако каждый из вариантов имеет лишь преимущество в объяснении одной из сторон ядерных сил. Удовлетворительной единой теории еще не существует. Наиболее приемлемой является псевдоскалярный вариант с псевдовекторной связью (из одного названия видно, что в этой теории здравым физическим смыслом и не пахнет - В.К.)”. Н.И. Карякин и др., Краткий справочник по физике, “Высшая школа”, М., 1962, стр. 428.
Здесь необходимо обратить внимание на то обстоятельство, что квантовая физика не объясняет причину отталкивания нуклонов в ядре, препятствующего "вкладыванию" нуклонов друг в друга под действием ядерных (гравидинамических) сил. В рамках развиваемых представлений ответ на этот вопрос очевиден: отталкивание нуклонов происходит под действием тех же гравидинамических сил при однонаправленном движении нейтрино сближающихся нуклонов, внутри которых они движутся встречно и притягиваются. “Эти опыты показали также, что на расстояниях 0,3 - 0,5 ферми между нуклонами возникают очень большие силы отталкивания (у нуклонов существует “отталкивающая сердцевина”) и что ядерные силы зависят не только от расстояния между взаимодействующими частицами, но и от взаимной ориентации их спинов и т.н. изотопических спинов... Некоторую аналогию для ядерных сил можно найти лишь в магнитном взаимодействии, зависящем от взаимной ориентации полюсов магнитов, но характер действия ядерных сил много сложнее”. Физика космоса, “Советская энциклопедия”, М., 1976, стр. 646-647. Отталкивание начинает превалировать над притяжением при сближении нуклонов на расстояние меньшее диаметра нуклона (около 1 фм). Сблизиться так, чтобы нейтрино в разных нуклонах двигались в противоположные стороны и притягивались, не дает общий гравидинамический момент нуклонов, т.к. в этом случае разноименные гравидинамические полюса их отталкиваются. Таким образом, единственным организующим стимулом ядер, так же, как и в случае атомов, да и в любых других случаях, является стремление системы к минимуму потенциальной энергии, который достигается минимумом потенциальной энергии каждого нуклона.
Здесь необходимо выяснить причины
устойчивости нейтронов в ядре, обуславливающей устойчивость и самих ядер. В
отличие от официальных представлений, новая физика объясняет устойчивость
нейтронов в ядре тем, что они находятся в мощном гравидинамическом поле,
которое превышает те значения, которые можно было бы достичь у
ультрарелятивистских нейтронов. Дефект массы при образовании ядра фактически
идет на упрочнение связей составляющих протона и нейтрона. “Однако
прежде чем идти дальше, поясним, почему в большинстве атомных ядер (большинство
их радиоактивны и так или иначе связаны именно с неустойчивостью нейтрона -
В.К) связанные в них нейтроны устойчивы и не распадаются, как свободный
нейтрон, в течение 15 мин. Причину этого следует искать в действии принципа
Паули, который в равной мере применим также к протонам и нейтронам ядра;
этот принцип очень сильно ограничивает (по существу запрещает)
распад нейтрона в ядре (так запрещает или нет? - В.К.) из-за отсутствия
там незанятых (вакантных) состояний, доступных для протонов с низкой энергией,
возникающих после распада нейтрона”. Фундаментальная структура материи, “Мир”,
М., 1984, стр. 82-83. Этому утверждению противоречит очень распространенный ![]() --распад
ядер, при котором образуются протоны с низкой энергией.
--распад
ядер, при котором образуются протоны с низкой энергией.
|
|
|
|
|
|
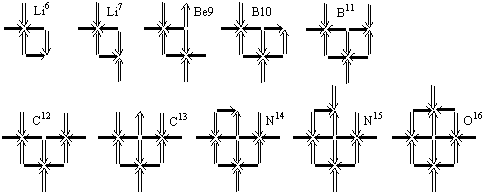
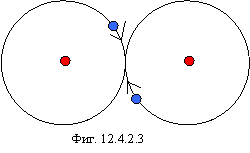
Рассмотрим строение некоторых изотопов с точки зрения выявления принципов построения любых ядер. Ядро 1H2 изображено на фигуре 12.1.
|
|
|
|
|
|
Плоскость орбит нейтрино в нуклонах перпендикулярна плоскости рисунка, направление движения нейтрино показано стрелками, причем нейтрон изображает (для удобства) сдвоенная стрелка большей длины, т.к. диаметр нейтрона в полтора раза больше протона. Пунктирными стрелками показано направление гравидинамического поля.
Существует только два возможных варианта
расположения нуклонов: "a" и
"b". Очевидно, что только
вариант "a" обеспечивает большую
глубину потенциальной ямы для каждого нуклона, поэтому он и реализуется. “... опыт показывает, что спин
дейтрона равен 1”. Н.И. Карякин и др., Краткий справочник по физике, “Высшая
школа”, М., 1962, стр. 421. Если говорить попросту, то протон и нейтрон в 1H2
вращаются в одну сторону (фиг. 12.1а), т.к.
официальная физика считает момент импульса нуклонов равным ![]() /2.
/2.
|
|
|
|
|
|
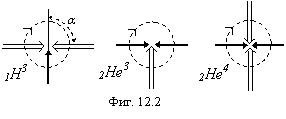
Ядра 1H3, 2He3
и 2He4 (![]() -частица) изображены на
фигуре 12.2. У дейтрона (фиг. 12.1а) протон в
небольшой степени оттягивает на себя электрон нейтрона, поэтому орбита
электрона немного увеличивается. Вместе с ней увеличивается на 0,02232
-частица) изображены на
фигуре 12.2. У дейтрона (фиг. 12.1а) протон в
небольшой степени оттягивает на себя электрон нейтрона, поэтому орбита
электрона немного увеличивается. Вместе с ней увеличивается на 0,02232![]() отрицательный магнитный момент электрона, который в свободном нейтроне
составляет -4,7057
отрицательный магнитный момент электрона, который в свободном нейтроне
составляет -4,7057![]() . На фигуре 12.2 гравидинамическое поле с
одной стороны стремится собрать все "витки" вместе, а с другой
стороны взаимное отталкивание протонов стремится их раздвинуть, поэтому для H3 угол
. На фигуре 12.2 гравидинамическое поле с
одной стороны стремится собрать все "витки" вместе, а с другой
стороны взаимное отталкивание протонов стремится их раздвинуть, поэтому для H3 угол ![]() составит 92,90, а для He3 87,80. С учетом
этих замечаний, магнитные моменты (в единицах ядерного магнетона) указанных
частиц будут совпадать с экспериментально найденными (Справочник химика, М.-Л.,
1963, стр.317): нейтрон –1,9130, протон 2,79270, дейтрон 0,85738, H3 2,9788, He3 –2,1274.
У He4
магнитный момент равен нулю из-за полной симметрии в расположении нуклонов.
составит 92,90, а для He3 87,80. С учетом
этих замечаний, магнитные моменты (в единицах ядерного магнетона) указанных
частиц будут совпадать с экспериментально найденными (Справочник химика, М.-Л.,
1963, стр.317): нейтрон –1,9130, протон 2,79270, дейтрон 0,85738, H3 2,9788, He3 –2,1274.
У He4
магнитный момент равен нулю из-за полной симметрии в расположении нуклонов.
|
|
|
|
|
|
Мы видим, что у ![]() -частицы
гравидинамическое поле в основном сосредоточено внутри тора, образованного
нуклонами, поэтому она является наиболее прочным элементом всех ядерных
структур (аналогия с инертными газами, имеющими полностью сформированный
8-электронный тор). По этой же причине две
-частицы
гравидинамическое поле в основном сосредоточено внутри тора, образованного
нуклонами, поэтому она является наиболее прочным элементом всех ядерных
структур (аналогия с инертными газами, имеющими полностью сформированный
8-электронный тор). По этой же причине две ![]() -частицы не могут
образовать прочные ядра (4Be8), т.к.
электростатическое отталкивание оказывается достаточным для разрушения такого
ядра из-за очень слабой гравидинамической связи. Из фигуры 12.1 и фигуры 12.2
становится понятным, почему не идет такой выгодный процесс, как: H2+H2
-частицы не могут
образовать прочные ядра (4Be8), т.к.
электростатическое отталкивание оказывается достаточным для разрушения такого
ядра из-за очень слабой гравидинамической связи. Из фигуры 12.1 и фигуры 12.2
становится понятным, почему не идет такой выгодный процесс, как: H2+H2![]() He4, а идут процессы: H2+H2
He4, а идут процессы: H2+H2![]() He3+n или H2+H2
He3+n или H2+H2![]() H3+p. Это обусловлено тем,
что для образования 2He4, два дейтрона надо
фактически предварительно разрушить и реагировать должны сразу четыре
образовавшиеся частицы. В условиях сверхвысоких давлений (и, конечно,
температур) возможен и такой процесс: 41H1
H3+p. Это обусловлено тем,
что для образования 2He4, два дейтрона надо
фактически предварительно разрушить и реагировать должны сразу четыре
образовавшиеся частицы. В условиях сверхвысоких давлений (и, конечно,
температур) возможен и такой процесс: 41H1![]() 2He4+2e++2
2He4+2e++2![]() при "рождении" новых звезд.
при "рождении" новых звезд.
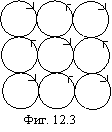
Чтобы ![]() -частицы
могли удерживаться гравидинамическим полем, необходимо гравидинамический поток
(сравним с магнитным потоком) разветвить, что показано на фигуре 12.3.
-частицы
могли удерживаться гравидинамическим полем, необходимо гравидинамический поток
(сравним с магнитным потоком) разветвить, что показано на фигуре 12.3.
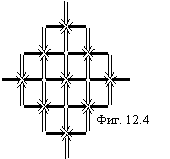
Для ![]() -частиц
это будет выглядеть, как показано на фигуре 12.4.
-частиц
это будет выглядеть, как показано на фигуре 12.4.
|
|
|
|
|
|
В такой квазикристаллической структуре все ![]() -частицы равноправны не
только между собой, но и с их соединительными узлами (которые неотличимы от
самих
-частицы равноправны не
только между собой, но и с их соединительными узлами (которые неотличимы от
самих ![]() -частиц),
поэтому она обладает исключительной прочностью. Для образования трехмерной
-частиц),
поэтому она обладает исключительной прочностью. Для образования трехмерной
Фиг. 12.5
структуры ![]() -частицы
накладываются на двумерную структуру, изображенную на фигуре 12.4 так, что
движение нейтрино в нуклонах будет противоположным. При этом прочность связи
между слоями
-частицы
накладываются на двумерную структуру, изображенную на фигуре 12.4 так, что
движение нейтрино в нуклонах будет противоположным. При этом прочность связи
между слоями ![]() -частиц
будет меньше, чем внутри слоя. Четность протонов и нейтронов в прочных ядрах
обусловлена тем, что с увеличением количества нуклонов в соединительном узле,
его прочность возрастает, но сам соединительный узел не может иметь больше двух
протонов и двух нейтронов, поэтому избыточные нейтроны предпочитают собираться
парами у соединительных узлов. Это правило является следствием
гравидинамического взаимодействия и позволяет изобразить на фигуре 12.5, в
качестве примера, все известные устойчивые изотопы до 8О16.
-частиц
будет меньше, чем внутри слоя. Четность протонов и нейтронов в прочных ядрах
обусловлена тем, что с увеличением количества нуклонов в соединительном узле,
его прочность возрастает, но сам соединительный узел не может иметь больше двух
протонов и двух нейтронов, поэтому избыточные нейтроны предпочитают собираться
парами у соединительных узлов. Это правило является следствием
гравидинамического взаимодействия и позволяет изобразить на фигуре 12.5, в
качестве примера, все известные устойчивые изотопы до 8О16.
Таким образом, у четно-четных ядер (с четным числом протонов и нейтронов) магнитные моменты нуклонов полностью скомпенсированы за исключением только некоторых ядер. “... все ядра, состоящие из четного числа протонов и четного числа нейтронов (т.н. четно-четные ядра), имеют в основном состоянии нулевой спин. Это говорит об определенной упорядоченности в движении нуклонов, приводящей к почти полной взаимной компенсации моментов количества движения отдельных нуклонов”. Физика микромира, “Советская энциклопедия”, М., 1980, стр. 500. При этом четность ядер в этой книге понимается только в математическом, но не ортодоксально-физическом смысле. “Важная характеристика состояния ядра - его четность. Это специфически квантовая характеристика, не имеющая классического аналога”. Там же, стр. 501.
Ядра атомов могут быть образованы тремя способами. Преимущественный способ образования - "холодная" конденсация нейтронов с последующим их превращением в протоны внутри ядра по мере необходимости. В чем состоит эта необходимость, станет ясно из дальнейшего. Второй способ образования - "горячий" в результате одной из разновидностей коллапса, о чем будем говорить в разделе, посвященном коллапсу. Этот же способ можно реализовать и "холодным" образом, наиболее перспективным для будущей энергетики. Третий способ известен - "горячий" синтез в звездах. Для уменьшения количества нуклонов в ядре существует только два пути - распад тяжелых ядер за счет радиоактивности или воздействие извне достаточной силы.
|
|
|
|
|
|
Начиная с ядра кислорода появляется энергетически выгодная возможность
на образовавшейся плоскости из четырех ![]() -частиц собрать новые
-частиц собрать новые ![]() -частицы
с последующей транспортировкой их по плоскости к месту назначения или без
таковой. При этом встраивающиеся в плоскость
-частицы
с последующей транспортировкой их по плоскости к месту назначения или без
таковой. При этом встраивающиеся в плоскость ![]() -частицы образуют наиболее
выгодную конфигурацию такую, чтобы обеспечить между
-частицы образуют наиболее
выгодную конфигурацию такую, чтобы обеспечить между ![]() -частицами
возможно большое число соединительных узлов с возможно большим числом нуклонов
в каждом узле. Поэтому Ne20 образует структуру, изображенную
на фигуре 12.6.
-частицами
возможно большое число соединительных узлов с возможно большим числом нуклонов
в каждом узле. Поэтому Ne20 образует структуру, изображенную
на фигуре 12.6.
Затем на плоскости ![]() -частиц
постепенно образуется еще одна точно такая же плоскость с обратным движением
нуклонов, при этом получается 20Ca40 ядро которого
условно можно изобразить так: Ca(55), где цифры в скобках обозначают число
-частиц
постепенно образуется еще одна точно такая же плоскость с обратным движением
нуклонов, при этом получается 20Ca40 ядро которого
условно можно изобразить так: Ca(55), где цифры в скобках обозначают число ![]() -плоскостей
и число частиц в каждой плоскости. Избыточные нейтроны, естественно, не могут
находиться внутри плоскости и все время оттесняются наружу.
“... радиус действия ядерных
сил несколько больше радиуса шара, в котором распределены протоны. Возможно,
что это связано также с тем, что нейтроны распределены по шару большего
радиуса”. Н.И. Карякин и др., Краткий справочник по физике, “Высшая школа”, М.,
1962, стр. 420. Например, одна из
-плоскостей
и число частиц в каждой плоскости. Избыточные нейтроны, естественно, не могут
находиться внутри плоскости и все время оттесняются наружу.
“... радиус действия ядерных
сил несколько больше радиуса шара, в котором распределены протоны. Возможно,
что это связано также с тем, что нейтроны распределены по шару большего
радиуса”. Н.И. Карякин и др., Краткий справочник по физике, “Высшая школа”, М.,
1962, стр. 420. Например, одна из ![]() -плоскостей
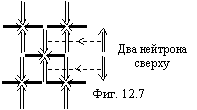
ядра изотопа 20Ca48 будет выглядеть, как показано на
фигуре 12.7. “При небольшом изменении числа нуклонов имеют место некоторые
нерегулярные изменения радиуса. Например, при переходе от 20Са40
к 20Са48 радиус распределения зарядов практически не
изменяется (что видно из фиг. 12.7 - В.К.). С точки
зрения исследования структуры ядра значительный интерес представляет
распределение в ядре и протонов и нейтронов. Так, оказалось, что нейтронный
радиус ядра Са48 примерно на 0,14×10-13
см больше протонного (это говорит о том, что внутри ядра находятся “чистые”
-плоскостей
ядра изотопа 20Ca48 будет выглядеть, как показано на
фигуре 12.7. “При небольшом изменении числа нуклонов имеют место некоторые
нерегулярные изменения радиуса. Например, при переходе от 20Са40
к 20Са48 радиус распределения зарядов практически не
изменяется (что видно из фиг. 12.7 - В.К.). С точки
зрения исследования структуры ядра значительный интерес представляет
распределение в ядре и протонов и нейтронов. Так, оказалось, что нейтронный
радиус ядра Са48 примерно на 0,14×10-13
см больше протонного (это говорит о том, что внутри ядра находятся “чистые” ![]() -частицы,
а нейтроны оттесняются в поверхностный слой - В.К.)”. Физика микромира,
“Советская энциклопедия”, М., 1980, стр. 499.
-частицы,
а нейтроны оттесняются в поверхностный слой - В.К.)”. Физика микромира,
“Советская энциклопедия”, М., 1980, стр. 499.
|
|
|
|
|
|
|
|
|
|
|
|
Естественно, что расстояние между нуклонами внутри ![]() -плоскости и между
плоскостями почти одинаково и составляет, примерно, 1 фм. В плоскость с 5
-плоскости и между
плоскостями почти одинаково и составляет, примерно, 1 фм. В плоскость с 5 ![]() -частицами возможно встроить 2
-частицами возможно встроить 2 ![]() частицы в
положении 1 (фиг. 12.6) с образованием 7 частиц и в положение 2 с образованием
замкнутой структуры из 9
частицы в
положении 1 (фиг. 12.6) с образованием 7 частиц и в положение 2 с образованием
замкнутой структуры из 9 ![]() -частиц к которой уже невыгодно что-либо
добавлять, кроме избыточных нейтронов. Таким образом, плоскости с 5, 7 и 9
-частиц к которой уже невыгодно что-либо
добавлять, кроме избыточных нейтронов. Таким образом, плоскости с 5, 7 и 9 ![]() -частицами
дают наиболее прочные ядра. Теперь мы можем изобразить структуру ядер: He(1), Ne(5), Ca(55), Ni(77), Kr(99), Pd(995), Sn(997), Xe(999), Gd(5999), W(59995),
Pt(79995), Pb(79997), U(579997),
No(5799975).
Очевидно, что практически любое ядро, в особенности сложное, можно представить
себе в виде нескольких изомеров, аналогично молекулам и элементарным частицам.
За свинцом подвижность
-частицами
дают наиболее прочные ядра. Теперь мы можем изобразить структуру ядер: He(1), Ne(5), Ca(55), Ni(77), Kr(99), Pd(995), Sn(997), Xe(999), Gd(5999), W(59995),
Pt(79995), Pb(79997), U(579997),
No(5799975).
Очевидно, что практически любое ядро, в особенности сложное, можно представить
себе в виде нескольких изомеров, аналогично молекулам и элементарным частицам.
За свинцом подвижность ![]() -частиц
как по
-частиц
как по ![]() -плоскости, так и внутри ее настолько
возрастает, что образование определенных структур сильно затрудняется.
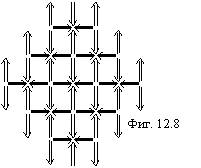
Избыточные нейтроны располагаются снаружи ядра. На фигуре 12.8 изображена
средняя плоскость изотопа 54Xe136 с 28 избыточными
нейтронами.
-плоскости, так и внутри ее настолько
возрастает, что образование определенных структур сильно затрудняется.
Избыточные нейтроны располагаются снаружи ядра. На фигуре 12.8 изображена
средняя плоскость изотопа 54Xe136 с 28 избыточными
нейтронами.
Из-за такого строения ядер и получается двугорбая кривая осколков, т.к. при не очень сильных воздействиях на ядро, оно разрушается по слабому месту вдоль a-плоскостей. “Теория предсказывает, что при делении должны наблюдаться симметричные осколки, т.е. с равными массами и равными зарядами, однако, эксперимент показывает, что осколки не симметричны.... Кривая “выход - массовое число” показывает, что максимальный выход, равный 6%, соответствует А=95 и А=139. Симметричное деление имеет выход около 10-2 %, т.е. это очень редкое явление”. Н.И. Карякин и др., Краткий справочник по физике, “Высшая школа”, М., 1962, стр. 478-479.
Теория ядра новой физики предсказывает,
что ядро урана, имеющего строение 579997 будет раскалываться при “слабом”
воздействии на него на несимметричные осколки по самому слабому месту вдоль ![]() -плоскостей с 9
-плоскостей с 9 ![]() -частицами, например, так: 579-997 или так: 5799-97 . В конечном итоге
должны получиться два осколка с суммарным числом
-частицами, например, так: 579-997 или так: 5799-97 . В конечном итоге
должны получиться два осколка с суммарным числом ![]() -частиц в них, равным 46. Очевидно, что эти осколки
должны иметь минимальную потенциальную энергию, т.е. быть максимально
симметричными с “магическим” числом нуклонов, например, Xe(999) и Kr(99),
но тогда сумма
-частиц в них, равным 46. Очевидно, что эти осколки
должны иметь минимальную потенциальную энергию, т.е. быть максимально
симметричными с “магическим” числом нуклонов, например, Xe(999) и Kr(99),
но тогда сумма ![]() -частиц
будет 45, следовательно, вместо Kr(99)
(любое изменение “идеального” ядра Xe
невыгодно), должен образоваться Sr(991). В подтверждение следующая цитата.
-частиц
будет 45, следовательно, вместо Kr(99)
(любое изменение “идеального” ядра Xe
невыгодно), должен образоваться Sr(991). В подтверждение следующая цитата.
“На самом же деле опыт показывает, что при делении ядер урана нейтронами, как правило, образуются осколки неравной величины. Около 95% осколков имеют массовые числа, лежащие в пределах от 85 до 105 и от 130 до 150, причем наиболее вероятно образование осколков, массовые числа которых лежат посередине этих интервалов, т.е. осколков, которые представляют собой ядра изотопов стронция 38Sr95 и ксенона 54Xe139”. Г.Е. Пустовалов, Атомная и ядерная физика, Изд. Московского университета, 1968, стр. 295-296.
В этой связи представляется весьма
вероятным распад очень неустойчивых ядер с образованием (кроме протона и ![]() -частицы) таких высокосимметричных ядер, как углерод,
кислород (фиг. 12.5) и неон (фиг. 12.6): “При изучении ядер, далеких от области
стабильности обнаружены новые типы радиоактивного распада: испускание протонов,
С12, С14, О16, Ne20
из основных состояний ядер”. Субатомная физика, Изд. Московского университета,
1994, стр.45.
-частицы) таких высокосимметричных ядер, как углерод,
кислород (фиг. 12.5) и неон (фиг. 12.6): “При изучении ядер, далеких от области
стабильности обнаружены новые типы радиоактивного распада: испускание протонов,
С12, С14, О16, Ne20
из основных состояний ядер”. Субатомная физика, Изд. Московского университета,
1994, стр.45.
Один из способов получения атомной
энергии может быть основан на скалывании тяжелых ядер. При скалывании ядер по ![]() -плоскостям образуются не шарообразные осколки, которые
быстро принимают шарообразную форму, при этом выделяется огромная энергия,
намного превышающая энергию, затраченную на скалывание.
-плоскостям образуются не шарообразные осколки, которые
быстро принимают шарообразную форму, при этом выделяется огромная энергия,
намного превышающая энергию, затраченную на скалывание.
За No возможности для укрупнения ядра практически
исчерпываются не только из-за ![]() -радиоактивности, но и по геометрическим соображениям,
т.к. ядро No практически точно
вписывается в шар. Размеры ядер почти точно соответствуют размерам, вычисляемым
по известным формулам. Хотя в ядрах и нет никаких замкнутых оболочек протонов
или нейтронов, тем не менее, указанная структура ядер полностью соответствует
так называемым "магическим" числам нуклонов в наиболее устойчивых
ядрах. Понятно, что самые неустойчивые ядра будут в начале образования новых
-радиоактивности, но и по геометрическим соображениям,
т.к. ядро No практически точно
вписывается в шар. Размеры ядер почти точно соответствуют размерам, вычисляемым
по известным формулам. Хотя в ядрах и нет никаких замкнутых оболочек протонов
или нейтронов, тем не менее, указанная структура ядер полностью соответствует
так называемым "магическим" числам нуклонов в наиболее устойчивых
ядрах. Понятно, что самые неустойчивые ядра будут в начале образования новых ![]() -плоскостей, с неполными
-плоскостей, с неполными ![]() -частицами и после наиболее устойчивых ядер:
-частицами и после наиболее устойчивых ядер:
Y (Kr+1,5![]() ) La (Xe+1,5
) La (Xe+1,5![]() ) At (Pb+1,5
) At (Pb+1,5![]() )
)
Nb (Kr+2,5![]() ) Pr (Xe+2,5
) Pr (Xe+2,5![]() ) Fr (Pb+2,5
) Fr (Pb+2,5![]() )
)
Tc (Kr+3,5![]() ) Pm (Xe+3,5
) Pm (Xe+3,5![]() ) Ac (Pb+3,5
) Ac (Pb+3,5![]() )
)
Отсюда непосредственно получаются
"магические числа неустойчивости" ядер с числом протонов в них: 39,
41, 43, 57, 59, 61, 85, 87, 89. Этот ряд легко продолжить в обе стороны. Хотя мы впервые отмечаем "магические числа
неустойчивости", следуя примеру официальной науки, приведем и
"магические числа устойчивости". Для протонов они непосредственно
получаются из самого строения ядер с полностью сформированными ![]() -плоскостями: 2(
-плоскостями: 2(![]() -частица), 8 (O), 10(Ne), 20(Ca), 28(Ni), 36(Kr),
46(Pd), 50(Sn),
54(Xe), 64(Gd),
74(W), 78(Pt), 82(Pb), 92(U), 102(No). Несколько особняком стоит ядро 14Si28
(151) в котором к плоскости из 5
-частица), 8 (O), 10(Ne), 20(Ca), 28(Ni), 36(Kr),
46(Pd), 50(Sn),
54(Xe), 64(Gd),
74(W), 78(Pt), 82(Pb), 92(U), 102(No). Несколько особняком стоит ядро 14Si28
(151) в котором к плоскости из 5 ![]() -частиц с двух сторон прилегают еще по одной, образуя симметричное
ядро, которое, как и все перечисленные, из-за своей симметричности обладает меньшей
потенциальной энергией, чем соседние ядра. "Магические числа"
нейтронов получаются также исходя из строения ядер, причем, они вторичны по
отношению к числам протонов. Например, изотоп 54Xe136
имеет три
-частиц с двух сторон прилегают еще по одной, образуя симметричное
ядро, которое, как и все перечисленные, из-за своей симметричности обладает меньшей
потенциальной энергией, чем соседние ядра. "Магические числа"
нейтронов получаются также исходя из строения ядер, причем, они вторичны по
отношению к числам протонов. Например, изотоп 54Xe136
имеет три ![]() -плоскости
с полностью заполненными вакантными местами нейтронов, поэтому одно из
"магических" чисел нейтронов будет: 136-54=82. При этом необходимо
иметь в виду, что результат вычислений должен соответствовать и формуле
-плоскости
с полностью заполненными вакантными местами нейтронов, поэтому одно из
"магических" чисел нейтронов будет: 136-54=82. При этом необходимо
иметь в виду, что результат вычислений должен соответствовать и формуле ![]() -устойчивости
ядра (см. ниже). Таким образом, "магические" числа никакого отношения
к ядерным оболочкам, которых нет, не имеют. “Особенно устойчивы те ядра, для
которых (при Z=N); Z=2; 8; 20 (дважды “магические числа)
или Z=28; 50; 82 и N=50, 82, 126 (“магические” числа)”. Н.И.
Карякин и др., Краткий справочник по физике, “Высшая школа”, М., 1962, стр.
422. Обратите внимание на то, что все ядра с “магическими” числами нуклонов симметричны,
поэтому и прочны. “Элементы с магическим числом нуклонов имеют близкий к нулю
квадрупольный момент, что говорит о симметричности этих ядер”. Там же, стр.
426.
-устойчивости
ядра (см. ниже). Таким образом, "магические" числа никакого отношения
к ядерным оболочкам, которых нет, не имеют. “Особенно устойчивы те ядра, для
которых (при Z=N); Z=2; 8; 20 (дважды “магические числа)
или Z=28; 50; 82 и N=50, 82, 126 (“магические” числа)”. Н.И.
Карякин и др., Краткий справочник по физике, “Высшая школа”, М., 1962, стр.
422. Обратите внимание на то, что все ядра с “магическими” числами нуклонов симметричны,
поэтому и прочны. “Элементы с магическим числом нуклонов имеют близкий к нулю
квадрупольный момент, что говорит о симметричности этих ядер”. Там же, стр.
426.
Процесс внутренней конверсии, когда возбужденное ядро излучает фотон, поглощаемый ближайшим орбитальным электроном, подтверждает ранее обсуждаемую возможность полного исчезновения фотона. “Внутренняя конверсия - процесс перехода ядра из состояния с большей энергией Еi в состояние с меньшей энергией Еf путем передачи избытка энергии непосредственно одному из электронов атомной оболочки. Электрон становится свободным, если сообщенная ему энергия Еi - Ef превышает его энергию связи Ве. Процесс внутренней конверсии осуществляется без участия реального фотона (с участием “виртуальных” фотонов - В.К.). Энергия передается электрону ядром главным образом за счет кулоновского взаимодействия”. Субатомная физика, Изд. Московского университета, 1994, стр. 56. Здесь мы опять замечаем, что представления официоза исходят из допущения того, что ближайший к ядру электрон и ядро взаимно информированы о состоянии друг друга. Кулоновское взаимодействие с ядром должно было бы проглотить электрон, а не выбросить его из атома.
Таким образом, ядра всех атомов внутри практически одинаковы и их свойства в основном определяет поверхностный слой, в котором основную роль играют “недостроенные” альфа-частицы, т.е. определенные места поверхности ядра. Этот факт открывает потенциальную возможность управления как скоростью распада посредством “прививок” так и направлением радиоактивного излучения посредством пространственной ориентации ядер.
|
|
|
|
|
|
Воспользовавшись энергиями связи ядер для H3 – 8,49 Мэв, He3 – 7,72 Мэв
и He4
– 28,3 Мэв, можно найти расстояние между протонами в He3 считая, что энергия
отталкивания между протонами 8,49-7,72=0,77 Мэв. Это
расстояние составляет 1,9·10-13 см. (Данные взяты из книги: Б.М. Яворский, А.А. Детлаф, Курс физики, М., 1967, т.3, стр.414).
На фигуре 12.9 в масштабе изображены частицы фигуры 12.2. Пунктиром обозначена
ось тора, диаметр ее 1,9 фм. Радиус протона 0,631 фм, радиус нейтрона (протон с
темным кольцом, изображающим электрон) 0,986 фм. Как видим, все размеры
соответствуют друг другу. Радиус ![]() -частицы
будет равен диаметру нейтрона 1,972 фм, по литературным данным (Физика
микромира, М., 1980, стр.499) он равен ~2
фм. По этим же данным плотность числа нуклонов внутри ядра одинакова и
равна, примерно, 1,68·1038 нуклонов/см3, а толщина
поверхностного слоя для всех ядер 1,5-2 фм. Эта величина соответствует диаметру
нейтронов, избыток которых вытесняется на поверхность. Объем
-частицы
будет равен диаметру нейтрона 1,972 фм, по литературным данным (Физика
микромира, М., 1980, стр.499) он равен ~2
фм. По этим же данным плотность числа нуклонов внутри ядра одинакова и
равна, примерно, 1,68·1038 нуклонов/см3, а толщина
поверхностного слоя для всех ядер 1,5-2 фм. Эта величина соответствует диаметру
нейтронов, избыток которых вытесняется на поверхность. Объем ![]() -частицы
равен 3,2106·10-38 см3. Плотность внутренней области
ядра, состоящей из
-частицы
равен 3,2106·10-38 см3. Плотность внутренней области
ядра, состоящей из ![]() -частиц
получится равной 2,07·1014 г/см3 (по литературным данным
Б.М. Яворский, А.А. Детлаф, Курс физики, М., 1967, т.3, стр.419) плотность
ядерного вещества составляет 1,3·1014 г/см3.
Соответственно, плотность нуклонов внутри ядра будет 1,25·1038
нуклонов/см3. Таким образом, расчеты подтверждают правильность
предыдущих рассуждений.
-частиц
получится равной 2,07·1014 г/см3 (по литературным данным
Б.М. Яворский, А.А. Детлаф, Курс физики, М., 1967, т.3, стр.419) плотность
ядерного вещества составляет 1,3·1014 г/см3.
Соответственно, плотность нуклонов внутри ядра будет 1,25·1038
нуклонов/см3. Таким образом, расчеты подтверждают правильность
предыдущих рассуждений.
Данными по энергии связи при образовании ![]() -частицы можно
воспользоваться для приблизительного расчета энергии связи (на один нуклон)
любых ядер. Предлагаемый метод расчета продемонстрируем на примере
доказательства, что ядро 28Ni58 является самым
устойчивым из всех ядер, т.к. у него максимальная энергия связи на один нуклон.
Можно предположить сразу, что кандидат на самое устойчивое ядро будет один из
ряда: Ca(55), Ni(77), Kr(99). У более легких
ядер симметричного строения слишком мало внутренних связей нуклонов, а у более
тяжелых энергия связи на один нуклон уменьшается по двум причинам: 1.
Возрастающее количество избыточных нейтронов практически не вносит
дополнительную энергию связи, т.к. они не образуют новых
-частицы можно
воспользоваться для приблизительного расчета энергии связи (на один нуклон)
любых ядер. Предлагаемый метод расчета продемонстрируем на примере
доказательства, что ядро 28Ni58 является самым
устойчивым из всех ядер, т.к. у него максимальная энергия связи на один нуклон.
Можно предположить сразу, что кандидат на самое устойчивое ядро будет один из
ряда: Ca(55), Ni(77), Kr(99). У более легких
ядер симметричного строения слишком мало внутренних связей нуклонов, а у более
тяжелых энергия связи на один нуклон уменьшается по двум причинам: 1.
Возрастающее количество избыточных нейтронов практически не вносит
дополнительную энергию связи, т.к. они не образуют новых ![]() -частиц, поэтому она в
расчете на один нуклон уменьшается, 2. Электростатическое отталкивание протонов
делает тяжелые ядра неустойчивыми.
-частиц, поэтому она в
расчете на один нуклон уменьшается, 2. Электростатическое отталкивание протонов
делает тяжелые ядра неустойчивыми.
|
|
|
|
|
|
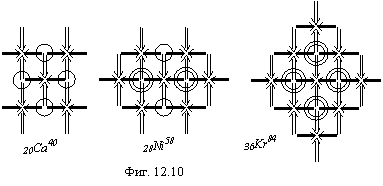
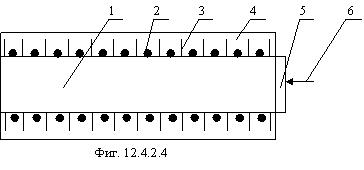
Указанные ядра имеют по две совершенно одинаковые ![]() -плоскости, поэтому для
удобства будем рассматривать только одну. Эти плоскости изображены на фигуре
12.10. У Ca40
избыточных нейтронов нет, поэтому число нуклонов в плоскости равно 20. Энергия
связи ядра будет равна сумме энергий связи 5
-плоскости, поэтому для
удобства будем рассматривать только одну. Эти плоскости изображены на фигуре
12.10. У Ca40
избыточных нейтронов нет, поэтому число нуклонов в плоскости равно 20. Энергия
связи ядра будет равна сумме энергий связи 5 ![]() -частиц плюс энергии связи
двух H3
и двух He3
(обозначены на фигуре 12.10 кружками).
-частиц плюс энергии связи
двух H3
и двух He3
(обозначены на фигуре 12.10 кружками).
|
|
|
|
|
|
Из этой суммы надо отнять энергию отталкивания, приходящуюся на один
протон (0,77 Мэв), умноженную на число протонов. При этом мы учитываем
отталкивание данного протона от ближайшего соседа и пренебрегаем
взаимодействием с другими протонами. Разделив на число нуклонов в плоскости
(20), найдем энергию связи на один нуклон E0. Таким образом: E0=(5·28,3+2·8,49+2·7,72-10·0,77):20=8,31
Мэв. У Ni58
два избыточных нейтрона, один из которых принадлежит к изображенной на фигуре ![]() -плоскости
(не показан), поэтому число нуклонов в ней будет 29. В общий баланс будет
входить энергия связи двух He3
и двух дополнительных
-плоскости
(не показан), поэтому число нуклонов в ней будет 29. В общий баланс будет
входить энергия связи двух He3
и двух дополнительных ![]() -частиц
(обозначены двойным кружком). Таким образом: E0=(9·28,3+2·7,72-14·0,77):29=8,94
Мэв. У Kr84
12 избыточных нейтронов, 6 из них принадлежат изображенной
-частиц
(обозначены двойным кружком). Таким образом: E0=(9·28,3+2·7,72-14·0,77):29=8,94
Мэв. У Kr84
12 избыточных нейтронов, 6 из них принадлежат изображенной ![]() -плоскости (не
показаны), поэтому число нуклонов в ней будет 42. Поэтому E0=(13·28,3-18·0,77):42=8,42
Мэв. Более точные математические выкладки дополнительного понимания не дадут,
но сильно загромоздят изложение. Таким образом, мы показали что представляют
собой
-плоскости (не
показаны), поэтому число нуклонов в ней будет 42. Поэтому E0=(13·28,3-18·0,77):42=8,42
Мэв. Более точные математические выкладки дополнительного понимания не дадут,
но сильно загромоздят изложение. Таким образом, мы показали что представляют
собой ![]() -частицы
и как они формируют ядра атомов.
-частицы
и как они формируют ядра атомов.
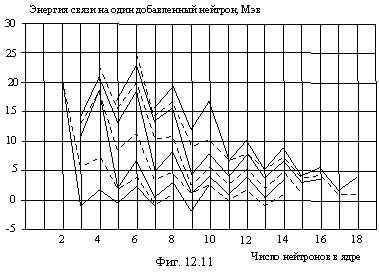
На фигуре 12.11 представлен график изменения энергии связи в Мэв на
один присоединенный нейтрон в зависимости от числа нейтронов в ядре. Ядра от He до Ne с четным числом
протонов показаны сплошной линией, а с нечетным числом протонов – пунктирной. He и Li образуют
по одной ![]() -частицы, Be и B в легких изотопах имеют по одной
-частицы, Be и B в легких изотопах имеют по одной ![]() -частицы
и по мере добавления нейтронов образуют вторую
-частицы
и по мере добавления нейтронов образуют вторую ![]() -частицу. C и N
в легких изотопах имеют по одной
-частицу. C и N
в легких изотопах имеют по одной ![]() -частицы
и по мере добавления нейтронов образуют вторую и третью
-частицы
и по мере добавления нейтронов образуют вторую и третью ![]() -частицы. O
и F в легких изотопах имеют по две
-частицы. O
и F в легких изотопах имеют по две ![]() -частицы и по мере
добавления нейтронов образуют третью и четвертую
-частицы и по мере
добавления нейтронов образуют третью и четвертую ![]() -частицы. Ne в
легких изотопах имеет три
-частицы. Ne в
легких изотопах имеет три ![]() -частицы и по мере добавления нейтронов
образует четвертую и пятую
-частицы и по мере добавления нейтронов
образует четвертую и пятую ![]() -частицу. Фигура 12.11 служит убедительным
подтверждением образования
-частицу. Фигура 12.11 служит убедительным
подтверждением образования ![]() -частиц
в ядре. Спаривание нейтронов дает заметный выигрыш в энергии связи из-за
образования структуры, в худшем случае, подобной H3 а, в лучшем случае,
подобной He4.
Общий спад кривых с увеличением числа нейтронов обусловлен тем, что в первую
очередь нейтроны встраиваются в места самые выгодные энергетически.
-частиц
в ядре. Спаривание нейтронов дает заметный выигрыш в энергии связи из-за
образования структуры, в худшем случае, подобной H3 а, в лучшем случае,
подобной He4.
Общий спад кривых с увеличением числа нейтронов обусловлен тем, что в первую
очередь нейтроны встраиваются в места самые выгодные энергетически.
Прежде, чем начать разговор о ![]() -распаде
ядер, необходимо несколько слов сказать о тепловом равновесии систем. Наши
классические представления о теплопередаче и тепловом равновесии в
изолированных системах не вызывают сомнений до тех пор, пока мы находимся на
атомно-молекулярном уровне. При переходе к системам другого уровня мы сразу
убеждаемся в том, что теплового равновесия между этими системами нет и быть не
может.
-распаде
ядер, необходимо несколько слов сказать о тепловом равновесии систем. Наши
классические представления о теплопередаче и тепловом равновесии в
изолированных системах не вызывают сомнений до тех пор, пока мы находимся на
атомно-молекулярном уровне. При переходе к системам другого уровня мы сразу
убеждаемся в том, что теплового равновесия между этими системами нет и быть не
может.
Рассмотрим некоторые примеры. Энергия
взаимодействия частиц при теплопередаче на атомно-молекулярном уровне
составляет порядка 0,1 эв, в то же время энергия взаимодействия электронов с
ядром составляет порядок 100 эв, что соответствует "температуре"
системы электронов вокруг ядра порядка миллиона градусов. Естественно, что о
"тепловом" равновесии системы атомных электронов и атомами, как
отдельными частицами не может быть речи, в противном случае атомы существовать
не могут. Переходя на уровень атомных ядер, представляющих собой как бы твердое
тело, в узлах кристаллической решетки которого находятся ![]() -частицы, мы одновременно переходим к взаимодействиям,
порядка 10 Мэв или "температуре" ядер атомов 1011 0K.
И, наконец, переходя на уровень нейтрино, составляющих нуклоны, с энергией
взаимодействия, порядка 100 Мэв, то их "температура" составит 1012
0K. К указанным уровням можно добавить и макроуровни:
планетарная система звезды, галактика. Очевидно, что теплообмена между всеми
перечисленными уровнями быть не может - это привело бы к автоматическому
исчезновению всех уровней, что и происходит периодически при коллапсе Вселенной
(см. главу о коллапсе), следовательно, законы термодинамики непригодны для
описания всех уровней совместно. Мало того, такие уровни, как
уровень нейтрино, уровень электронной системы атомов и макроуровни качественно
отличаются от уровней атомно-молекулярного и ядерного тем, что даже внутри этих
уровней "температура" каждого члена своя и "теплообмен"
невозможен из-за упорядоченности движения составляющих его частей, т.е.
термодинамика неприменима и к каждому из этих уровней в отдельности.
Здесь следует заметить, что в некоторой степени, обмен энергией составляющих
макроуровней возможен из-за диссипативных процессов в макромире, поэтому
макроуровни для своего существования требуют постоянной подпитки энергией (см.
главу о строении и образовании Солнечной системы). Интересующий нас сейчас
ядерный уровень аналогичен атомно-молекулярному в
смысле возможности энергообмена внутри ядра и применения термодинамических
законов для описания ядерных процессов. Это обстоятельство позволяет
воспользоваться отработанным до совершенства математическим аппаратом
термодинамики, в частности, описывающим химическое равновесие.
-частицы, мы одновременно переходим к взаимодействиям,
порядка 10 Мэв или "температуре" ядер атомов 1011 0K.
И, наконец, переходя на уровень нейтрино, составляющих нуклоны, с энергией
взаимодействия, порядка 100 Мэв, то их "температура" составит 1012
0K. К указанным уровням можно добавить и макроуровни:
планетарная система звезды, галактика. Очевидно, что теплообмена между всеми
перечисленными уровнями быть не может - это привело бы к автоматическому
исчезновению всех уровней, что и происходит периодически при коллапсе Вселенной
(см. главу о коллапсе), следовательно, законы термодинамики непригодны для
описания всех уровней совместно. Мало того, такие уровни, как
уровень нейтрино, уровень электронной системы атомов и макроуровни качественно
отличаются от уровней атомно-молекулярного и ядерного тем, что даже внутри этих
уровней "температура" каждого члена своя и "теплообмен"
невозможен из-за упорядоченности движения составляющих его частей, т.е.
термодинамика неприменима и к каждому из этих уровней в отдельности.
Здесь следует заметить, что в некоторой степени, обмен энергией составляющих
макроуровней возможен из-за диссипативных процессов в макромире, поэтому
макроуровни для своего существования требуют постоянной подпитки энергией (см.
главу о строении и образовании Солнечной системы). Интересующий нас сейчас
ядерный уровень аналогичен атомно-молекулярному в
смысле возможности энергообмена внутри ядра и применения термодинамических
законов для описания ядерных процессов. Это обстоятельство позволяет
воспользоваться отработанным до совершенства математическим аппаратом
термодинамики, в частности, описывающим химическое равновесие.
“Ядерные реакции коренным образом отличаются от химических реакций, при которых атомные ядра остаются неизменными, а в процессе принимают участие лишь внешние электроны атомов. Тем не менее, к ядерным превращениям могут быть приложены закономерности и уравнения химической термодинамики, так как термодинамика в своей основе не связана с определенными представлениями о структуре и свойствах отдельных частиц. Закономерности химической термодинамики, поэтому приложимы к превращениям веществ, взаимодействующих в стехиометрических количествах, хотя бы эти превращения не имели химического характера”. Я.И. Герасимов и др., Курс физической химии, Изд. химической литературы, М., 1963, том 1, стр. 343.
Такое мощное средство исследования как термодинамика явно недооценивается современной физикой ядра для описания ядерных процессов по двум причинам: 1. Физики связаны специфическими квантовыми законами, придуманными ими для микромира. В частности, по их представлениям нуклоны обладают полуцелым спином и подчиняются принципу запрета Паули (фермионы) - каждый нуклон ядра “знает” все о членах ядра, чтобы быть в состоянии, отличающимся от них, в то же время, термодинамика предполагает, что все члены термодинамической системы являются “бозонами”, т.е. “независимыми” друг от друга частицами. 2. Узкая специализация ученых заставляет термодинамикой заниматься физико-химиков и химиков, но не физиков-ядерщиков. Честно говоря, физиков не следует пускать в термодинамику, чтобы там не нагородили много лишнего.
Учитывая высокую "температуру" нуклонов в ядре, представляется очевидным, что при их столкновениях энергии достаточно как для образования пар нейтрино-антинейтрино, так и для образования электронно-позитронных пар. В результате в ядре устанавливается некоторая равновесная концентрация электронов и позитронов, как следствие следующих процессов (без учета нейтрино):
![]()
![]() (12.1.1)
(12.1.1)
![]()
![]() (12.1.2)
(12.1.2)
![]()
![]() (12.1.3)
(12.1.3)
![]()
![]() (12.1.4)
(12.1.4)
![]()
![]() (12.1.5).
(12.1.5).
Здесь необходимо подчеркнуть, что все участвующие в этих процессах частицы
находятся внутри ядра, т.е. в сильных внешних гравидинамических полях, поэтому
их свойства в большой степени отличаются от свойств свободных
частиц. Константа равновесия K3 учитывает и электронный
захват, но он не влияет на конечные выводы по той причине, что в этом процессе
участвует одно и то же число ближайших к ядру электронов вне зависимости от
заряда ядра. При увеличении заряда ядра уменьшается равновесная концентрация
электронов в результате смещения равновесия (12.1.4) вправо, при этом растет
равновесная концентрация позитронов, а при увеличении числа нейтронов в ядре
связываются позитроны в результате смещения равновесия процесса (12.1.3) вправо
и при этом растет равновесная концентрация электронов. Рост равновесной
концентрации позитронов или электронов происходит в результате смещения
равновесия процессов (12.1.1) и (12.1.2) влево. Поэтому, при определенном
количестве a-частиц
в ядре, оно будет наиболее устойчивым только при определенном количестве
избыточных нейтронов. В то же время возможен некоторый диапазон ![]() -устойчивых
ядер по обе стороны такого наиболее устойчивого ядра, как для некоторого
диапазона избыточных нейтронов при определенном Z, так и при одном и том
же количестве избыточных нейтронов - для некоторого диапазона
-устойчивых
ядер по обе стороны такого наиболее устойчивого ядра, как для некоторого
диапазона избыточных нейтронов при определенном Z, так и при одном и том
же количестве избыточных нейтронов - для некоторого диапазона ![]() -частиц,
составляющих ядро. Ширина диапазона пропорциональна глубине потенциальной ямы
наиболее устойчивого ядра. Ширина диапазона
-частиц,
составляющих ядро. Ширина диапазона пропорциональна глубине потенциальной ямы
наиболее устойчивого ядра. Ширина диапазона ![]() -частиц, при определенном
количестве избыточных нейтронов (нечетном), для ядер с нечетным Z может
оказаться равной нулю. В этом случае ядро испускает одновременно
-частиц, при определенном
количестве избыточных нейтронов (нечетном), для ядер с нечетным Z может
оказаться равной нулю. В этом случае ядро испускает одновременно ![]() и
и ![]() излучение.
Очевидно, что наиболее устойчивым (оптимальным по составу) ядро будет в том
случае, когда
излучение.
Очевидно, что наиболее устойчивым (оптимальным по составу) ядро будет в том
случае, когда ![]() , т.е. концентрация "свободных"
электронов и позитронов в ядре будет минимальной, поэтому будем искать
отношение:
, т.е. концентрация "свободных"
электронов и позитронов в ядре будет минимальной, поэтому будем искать
отношение: ![]() .
.
Из
(12.1.3): ![]() (12.1.6),
(12.1.6),
Из (12.1.4):
![]() (12.1.7),
(12.1.7),
Из
(12.1.5):
![]() (12.1.8).
(12.1.8).
Подставим (12.1.8) в (12.1.6):
![]() (12.1.9).
(12.1.9).
Из (12.1.7) и (12.1.9):
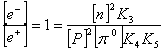 (12.1.10).
(12.1.10).
Из
(12.1.10):
![]() (12.1.11).
(12.1.11).
Здравый смысл подсказывает, что, в
первом приближении, ![]() будет пропорциональна числу нуклонов в
ядре. Ортодоксальная физика также признает существование пионов в ядре, правда,
по другим причинам: “Вследствие закона сохранения энергии эти частицы
удерживаются “взаперти”, в ядре, до тех пор, пока извне не поступит энергия,
превосходящая mc2 (m - масса частиц)”. Фундаментальная
структура материи, “Мир”, М., 1984, стр. 84.
будет пропорциональна числу нуклонов в
ядре. Ортодоксальная физика также признает существование пионов в ядре, правда,
по другим причинам: “Вследствие закона сохранения энергии эти частицы
удерживаются “взаперти”, в ядре, до тех пор, пока извне не поступит энергия,
превосходящая mc2 (m - масса частиц)”. Фундаментальная
структура материи, “Мир”, М., 1984, стр. 84.
Тогда (12.1.11) можно переписать в следующем виде:
![]() (12.1.12).
(12.1.12).
При этом изменение констант равновесия и ![]() , конечно, будет зависеть
от конкретного строения ядра, но является эффектом второго порядка. Очевидно, что для тяжелых ядер зависимость (12.1.12) не будет выполняться,
во-первых, из-за того, что вероятность образования
, конечно, будет зависеть
от конкретного строения ядра, но является эффектом второго порядка. Очевидно, что для тяжелых ядер зависимость (12.1.12) не будет выполняться,
во-первых, из-за того, что вероятность образования ![]() уже не
будет зависеть от числа нуклонов в ядре и, во-вторых, из-за того, что число
нуклонов на поверхности ядра будет составлять все меньшую долю от общего числа
нуклонов в ядре, а внутри ядра отношение n/P=1. Поэтому,
отношение n/P в реальных ядрах вначале увеличивается до значений 1,58, а
затем падает (после 96Cm247) в пределе стремясь к
единице. Этот вывод нам пригодится при обсуждении различных сценариев коллапса
и возможности существования нейтронных макротел. Поскольку избыточные нейтроны
располагаются на поверхности ядра, которая растет медленнее, чем объем, то для
супертяжелых ядер геометрические соображения требуют стремления к единице
отношения числа протонов к нейтронам, а термодинамические требуют следования
формуле
уже не
будет зависеть от числа нуклонов в ядре и, во-вторых, из-за того, что число
нуклонов на поверхности ядра будет составлять все меньшую долю от общего числа
нуклонов в ядре, а внутри ядра отношение n/P=1. Поэтому,
отношение n/P в реальных ядрах вначале увеличивается до значений 1,58, а
затем падает (после 96Cm247) в пределе стремясь к
единице. Этот вывод нам пригодится при обсуждении различных сценариев коллапса
и возможности существования нейтронных макротел. Поскольку избыточные нейтроны
располагаются на поверхности ядра, которая растет медленнее, чем объем, то для
супертяжелых ядер геометрические соображения требуют стремления к единице
отношения числа протонов к нейтронам, а термодинамические требуют следования
формуле ![]() -устойчивости
ядер, по которой число избыточных нейтронов должно прогрессивно нарастать. Этот
конфликт исчерпывается компромиссом на ядре урана, поэтому надежды ученых найти
"островок стабильности" в трансурановых ядрах призрачны до тех пор,
пока мы не научимся делать плоские или линейные ядра, чему благоприятствует электростатическое
отталкивание протонов, но мешает короткодействующее и сильное гравидинамическое
взаимодействие.
-устойчивости
ядер, по которой число избыточных нейтронов должно прогрессивно нарастать. Этот
конфликт исчерпывается компромиссом на ядре урана, поэтому надежды ученых найти
"островок стабильности" в трансурановых ядрах призрачны до тех пор,
пока мы не научимся делать плоские или линейные ядра, чему благоприятствует электростатическое
отталкивание протонов, но мешает короткодействующее и сильное гравидинамическое
взаимодействие.
Для того чтобы ясно видеть, какие изотопы элементов имеют состав ядер
близкий к оптимальному, удобно все известные изотопы
элементов представить в виде двух аналогичных таблиц. В одной таблице в первом
столбце отложено целое число ![]() -частиц,
составляющих ядро - этому соответствуют элементы с четным числом протонов в ядре.
В последующих столбцах располагаются изотопы с 1, 2, 3 и т.д. избыточными
относительно целого числа
-частиц,
составляющих ядро - этому соответствуют элементы с четным числом протонов в ядре.
В последующих столбцах располагаются изотопы с 1, 2, 3 и т.д. избыточными
относительно целого числа ![]() -частиц
нейтронами. Таким образом, все изотопы каждого элемента с
четным Z в этой таблице занимают определенную строку. Другая
таблица построена аналогично, разница лишь в том, что в первом столбце отложено
целое число
-частиц
нейтронами. Таким образом, все изотопы каждого элемента с
четным Z в этой таблице занимают определенную строку. Другая
таблица построена аналогично, разница лишь в том, что в первом столбце отложено
целое число ![]() -частиц,
включая одну недостроенную, т.е. с недостатком одного протона - этому
соответствуют элементы с нечетным числом протонов. Эти таблицы дают очень ясную
картину свойств ядер. Все устойчивые изотопы элементов занимают определенный
диапазон в столбцах, выше которого располагаются
-частиц,
включая одну недостроенную, т.е. с недостатком одного протона - этому
соответствуют элементы с нечетным числом протонов. Эти таблицы дают очень ясную
картину свойств ядер. Все устойчивые изотопы элементов занимают определенный
диапазон в столбцах, выше которого располагаются ![]() радиоактивные изотопы
(заряд ядра слишком мал, при данном числе избыточных нейтронов), а ниже
располагаются
радиоактивные изотопы
(заряд ядра слишком мал, при данном числе избыточных нейтронов), а ниже
располагаются ![]() - радиоактивные изотопы (заряд ядер
слишком велик при этом же числе избыточных нейтронов). В таблицах очень ярко
проявляется влияние четности зарядов ядер и четности избыточных нейтронов на
прочность ядер и, следовательно, их устойчивость к
- радиоактивные изотопы (заряд ядер
слишком велик при этом же числе избыточных нейтронов). В таблицах очень ярко
проявляется влияние четности зарядов ядер и четности избыточных нейтронов на
прочность ядер и, следовательно, их устойчивость к ![]() -радиоактивности. Эти
таблицы ввиду их громоздкости здесь не приводятся.
-радиоактивности. Эти
таблицы ввиду их громоздкости здесь не приводятся.
|
|
|
|
|
|
Из формулы (12.1.12) видно, что с увеличением числа нуклонов в ядре,
число избыточных нейтронов должно прогрессивно возрастать, чтобы сохранить ![]() -устойчивость
ядер. Поэтому избыточные нейтроны все в большей степени разрыхляют поверхность
ядра, что приводит к резкому сокращению диапазонов устойчивых ядер, с
увеличением числа нуклонов в ядре, до такой степени, что в тяжелых ядрах
преимущественной становится
-устойчивость
ядер. Поэтому избыточные нейтроны все в большей степени разрыхляют поверхность
ядра, что приводит к резкому сокращению диапазонов устойчивых ядер, с
увеличением числа нуклонов в ядре, до такой степени, что в тяжелых ядрах
преимущественной становится ![]() -радиоактивность
даже для ядер с избытком нейтронов относительно оптимального состава
(первопричиной этого, конечно, является сильно возрастающее отталкивание
-радиоактивность
даже для ядер с избытком нейтронов относительно оптимального состава
(первопричиной этого, конечно, является сильно возрастающее отталкивание ![]() -частиц
из-за электростатического взаимодействия с ядром в целом). Из этих же таблиц
хорошо видны изотопы, ядра которых оптимальны или близки к этому: это изотопы с
устойчивым ядром, оказавшиеся в столбцах в одиночестве, диапазоны, состоящие
всего из двух устойчивых изотопов, изотопы, содержание которых составляет 100%
какого-либо элемента в естественных условиях, а также изотопы с одновременной
-частиц
из-за электростатического взаимодействия с ядром в целом). Из этих же таблиц
хорошо видны изотопы, ядра которых оптимальны или близки к этому: это изотопы с
устойчивым ядром, оказавшиеся в столбцах в одиночестве, диапазоны, состоящие
всего из двух устойчивых изотопов, изотопы, содержание которых составляет 100%
какого-либо элемента в естественных условиях, а также изотопы с одновременной ![]() -радиоактивностью
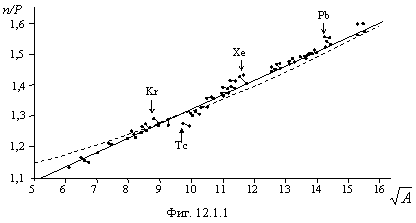
(один или два в столбце). Все эти изотопы нанесены на фигуре 12.1.1 в
координатах:
-радиоактивностью
(один или два в столбце). Все эти изотопы нанесены на фигуре 12.1.1 в
координатах: ![]() - n/P и достаточно хорошо
укладываются на прямую, что подтверждает справедливость формулы (12.1.12). Пары изотопов, относящиеся к одному столбцу таблиц соединены
отрезком прямой. Как и ожидалось, точки не точно укладываются на прямую, а образуют несколько выпуклых вверх кривых, изломы
которых соответствуют максимально и минимально устойчивым ядрам, т.е. заметна
внутренняя структура ядер.
- n/P и достаточно хорошо
укладываются на прямую, что подтверждает справедливость формулы (12.1.12). Пары изотопов, относящиеся к одному столбцу таблиц соединены
отрезком прямой. Как и ожидалось, точки не точно укладываются на прямую, а образуют несколько выпуклых вверх кривых, изломы
которых соответствуют максимально и минимально устойчивым ядрам, т.е. заметна
внутренняя структура ядер.
Уравнение прямой фиг. 12.1.1:
![]() (12.1.13).
(12.1.13).
Интересно определить, при каких значениях A отношение n/P<1,
т.е. оптимальный состав ядер будет содержать избыток протонов в сравнении с
нейтронами. Приравняв (12.1.13) единице, найдем: n/P<1 при A<12.
Установленное свойство ядер должно проявляться у нечетных ядер сильней, т.к.
прочность их значительно меньше. Этим и объясняется устойчивость всего четырех
известных нечетно-нечетных ядер: 7N14, 5B10,
3Li6, 1H2. Мало того,
становится понятной ![]() -радиоактивность
трития и устойчивость единственного ядра, у которого число протонов превышает
число нейтронов (за исключением протия) 2He3, хотя
распространенность этого изотопа гелия невелика, т.к. замыкание
гравидинамического поля внутри тора 2He4 намного
выгоднее энергетически.
-радиоактивность
трития и устойчивость единственного ядра, у которого число протонов превышает
число нейтронов (за исключением протия) 2He3, хотя
распространенность этого изотопа гелия невелика, т.к. замыкание
гравидинамического поля внутри тора 2He4 намного
выгоднее энергетически.
Соотношение между нейтронами и протонами для устойчивых ядер известно из полуэмпирического выражения капельной модели ядра:
![]() (12.1.14).
(12.1.14).
Подставляя в числитель A=P+n и преобразуя, найдем:
![]() (12.1.15).
(12.1.15).
Кривая (12.1.15) нанесена пунктиром на
график фигуры 12.1.1, откуда видно, что известная формула хуже отражает
реальное положение вещей, чем предлагаемая (12.1.13). Условие n/P <1
будет выполняться для (12.1.15) при A<1,5, т.е. не выполняется для
любых известных изотопов, кроме 1H1, но это не в
счет, т.к. отдельному протону не с кем обмениваться энергией. Поэтому (12.1.15)
не объясняет устойчивость 2He3 в сравнении с 1H3.
Известны и другие уравнения, практически не отличающиеся от
приведенного, например: ![]() . (Н.И. Карякин и др., Краткий справочник по
физике, “Высшая школа”, М., 1962, стр. 422).
. (Н.И. Карякин и др., Краткий справочник по
физике, “Высшая школа”, М., 1962, стр. 422).
12.2. Об электронном захвате,
нейтронном и ![]() -распаде
-распаде
Механизм электронного захвата на
основании вышеизложенного становится ясен. Он обусловлен
термодинамической необходимостью образовать более устойчивое ядро,
скомпенсировав избыточную концентрацию позитронов, причем, в принципиальном
плане не имеет значения, происходит ли это за счет испускания позитрона или
захвата электрона с ближайшего окружения ядра, выбор зависит только от
энергетической выгодности. Если у ![]() -распада нет альтернативы, то электронный захват имеет
преимущество перед испусканием позитронов по той причине, что захватить
ближайший к ядру электрон выгодней из-за электростатического и
гравидинамического притяжения к ядру, в то время, как позитрон должен пройти
некоторое расстояние внутри ядра, рискуя быть связанным в процессах (12.1.1),
(12.1.2), (12.1.3), при этом никак не взаимодействуя с ним электростатически и,
кроме того, преодолеть барьер гравидинамического притяжения на выходе из ядра
(работа выхода). Поэтому
-распада нет альтернативы, то электронный захват имеет
преимущество перед испусканием позитронов по той причине, что захватить
ближайший к ядру электрон выгодней из-за электростатического и
гравидинамического притяжения к ядру, в то время, как позитрон должен пройти
некоторое расстояние внутри ядра, рискуя быть связанным в процессах (12.1.1),
(12.1.2), (12.1.3), при этом никак не взаимодействуя с ним электростатически и,
кроме того, преодолеть барьер гравидинамического притяжения на выходе из ядра
(работа выхода). Поэтому ![]() распад в чистом виде
мы наблюдаем только у ядер, по составу далеких от оптимального,
т.е. с высокой избыточной концентрацией электронов или позитронов.
распад в чистом виде
мы наблюдаем только у ядер, по составу далеких от оптимального,
т.е. с высокой избыточной концентрацией электронов или позитронов.
“На самом деле захвата электрона ядром, разумеется, не происходит. Превращение протона в нейтрон в ядре сопровождается одновременным исчезновением электрона на К-оболочке”. Б.М. Яворский, А.А. Детлаф, Курс физики, “Высшая школа”, М., 1967, стр. 461. “Чудесное” исчезновение электрона при превращении протона в нейтрон является следствием глубоко ошибочных изначальных представлений ортодоксальной физики, касающихся микромира.
Формулу (12.1.13) можно удовлетворить,
т.е. привести нейтронно-протонный состав ядра к оптимальному не только путем ![]() распада
или электронного захвата, но и испусканием избыточных нейтронов и
распада
или электронного захвата, но и испусканием избыточных нейтронов и ![]() -частиц,
но не протонов, поскольку "лишних" протонов в ядре нет (за
исключением “недостроенных”
-частиц,
но не протонов, поскольку "лишних" протонов в ядре нет (за
исключением “недостроенных” ![]() -частиц), все они входят в
состав
-частиц), все они входят в
состав ![]() -частиц, которые разрушить очень трудно. При
испускании нейтрона отношение n/P уменьшается непосредственно, а при
испускании
-частиц, которые разрушить очень трудно. При
испускании нейтрона отношение n/P уменьшается непосредственно, а при
испускании ![]() -частицы
это отношение фактически увеличивается за счет избыточных нейтронов в ядре,
несмотря на то, что в самой
-частицы
это отношение фактически увеличивается за счет избыточных нейтронов в ядре,
несмотря на то, что в самой ![]() -частице отношение n/P=1. Естественно,
что нейтронный и
-частице отношение n/P=1. Естественно,
что нейтронный и ![]() -распад
будут наблюдаться только при максимальном отклонении состава ядра от
оптимального, т.к. "выдрать" их из ядерной решетки не так просто.
-распад
будут наблюдаться только при максимальном отклонении состава ядра от
оптимального, т.к. "выдрать" их из ядерной решетки не так просто. ![]() -распад
представляет собой почти полную аналогию с испарением молекулы с поверхности
твердого тела, с учетом того, что "теплота испарения" для каждого
изотопа своя и определяется степенью разрыхленности поверхности ядра
избыточными нейтронами и другими факторами, влияющими на прочность ядра.
Поэтому “у некоторых элементов наблюдаются так называемые длиннопробежные
-распад
представляет собой почти полную аналогию с испарением молекулы с поверхности
твердого тела, с учетом того, что "теплота испарения" для каждого
изотопа своя и определяется степенью разрыхленности поверхности ядра
избыточными нейтронами и другими факторами, влияющими на прочность ядра.
Поэтому “у некоторых элементов наблюдаются так называемые длиннопробежные ![]() -частицы,
имеющие вполне определенную, но большую энергию, чем основная масса
-частицы,
имеющие вполне определенную, но большую энергию, чем основная масса ![]() -частиц.
Наличие таких частиц объясняется тем, что перед
-частиц.
Наличие таких частиц объясняется тем, что перед ![]() -распадом
-распадом ![]() -частица может получить дополнительную энергию” (Н.И.
Карякин и др., Краткий справочник по физике, “Высшая школа”, М., 1962, стр.
460). К этому нужно только добавить, что, по представлениям новой физики,
длиннопробежные
-частица может получить дополнительную энергию” (Н.И.
Карякин и др., Краткий справочник по физике, “Высшая школа”, М., 1962, стр.
460). К этому нужно только добавить, что, по представлениям новой физики,
длиннопробежные ![]() -частицы
“испаряются” из того места
-частицы
“испаряются” из того места ![]() -плоскостей, где “теплота испарения” их
больше, а дополнительную энергию эти частицы получают за счет больцмановского
распределения энергии среди нуклонов.
-плоскостей, где “теплота испарения” их
больше, а дополнительную энергию эти частицы получают за счет больцмановского
распределения энергии среди нуклонов.
Поэтому закон Гейгера-Нэттола для ![]() -распада
аналогичен закону Клаузиуса-Клапейрона для давления насыщенного пара в
зависимости от температуры. С увеличением заряда ядра "теплота
испарения"
-распада
аналогичен закону Клаузиуса-Клапейрона для давления насыщенного пара в
зависимости от температуры. С увеличением заряда ядра "теплота
испарения" ![]() -частиц
уменьшается из-за электростатического отталкивания до такой степени, что у
трансурановых элементов
-частиц
уменьшается из-за электростатического отталкивания до такой степени, что у
трансурановых элементов ![]() -распад является подавляющим в конкуренции с
-распад является подавляющим в конкуренции с ![]() -распадом
и электронным захватом.
-распадом
и электронным захватом.
“Гейгер и Нэттол установили очень важное
соотношение между энергиями Е ![]() -частиц и периодами
полураспада. Обычно его выражают в виде связи между пробегом и постоянной
распада: lgR = Alg
-частиц и периодами
полураспада. Обычно его выражают в виде связи между пробегом и постоянной
распада: lgR = Alg![]() + B.
(Здесь R - пробег
+ B.
(Здесь R - пробег ![]() -частицы,
а
-частицы,
а ![]() - постоянная распада - обратная величина времени жизни
- В.К.). Константа А, определяющая наклон
прямой в координатах (lgR, lg
- постоянная распада - обратная величина времени жизни
- В.К.). Константа А, определяющая наклон
прямой в координатах (lgR, lg![]() ), имеет практически одно и то же значение для всех
трех радиоактивных рядов. “В” имеет различные значения для различных
рядов. Закон Гейгера - Нэттола показывает, что ядра, испускающие
), имеет практически одно и то же значение для всех
трех радиоактивных рядов. “В” имеет различные значения для различных
рядов. Закон Гейгера - Нэттола показывает, что ядра, испускающие ![]() -частицы
с большей энергией, должны иметь меньший период полураспада, при этом небольшое
различие в энергиях должно приводить к очень большому различию в периодах
полураспада”. Н.И. Карякин и др., Краткий справочник по физике, “Высшая школа”,
М., 1962, стр. 458.
-частицы
с большей энергией, должны иметь меньший период полураспада, при этом небольшое
различие в энергиях должно приводить к очень большому различию в периодах
полураспада”. Н.И. Карякин и др., Краткий справочник по физике, “Высшая школа”,
М., 1962, стр. 458.
Поскольку “теплота испарения” ![]() -частицы
сильно зависит от строения ядра так же, как и теплота испарения молекул
вещества от температуры, то наиболее подходящим для сравнения будет уравнение
Клаузиуса-Клапейрона в виде:
-частицы
сильно зависит от строения ядра так же, как и теплота испарения молекул
вещества от температуры, то наиболее подходящим для сравнения будет уравнение
Клаузиуса-Клапейрона в виде:
![]() , где р2 - давление насыщенного пара второй
жидкости, р1 - давление насыщенного пара первой жидкости,
, где р2 - давление насыщенного пара второй
жидкости, р1 - давление насыщенного пара первой жидкости, ![]() 2 и
2 и ![]() 1 -
соответствующие теплоты испарения, Т1,кр и Т2,кр
- соответствующие критические температуры, с - постоянная для данной
пары жидкостей (Я.И. Герасимов и др., Курс физической химии, Госхимиздат, М.,
1963, стр. 153). Здесь, как и в законе Гейгера-Нэттола постоянная А имеет практически одно и то же значение (если
“первая” - жидкость сравнения - одна и та же), а постоянная “с” зависит
от свойств второй жидкости.
1 -
соответствующие теплоты испарения, Т1,кр и Т2,кр
- соответствующие критические температуры, с - постоянная для данной
пары жидкостей (Я.И. Герасимов и др., Курс физической химии, Госхимиздат, М.,
1963, стр. 153). Здесь, как и в законе Гейгера-Нэттола постоянная А имеет практически одно и то же значение (если
“первая” - жидкость сравнения - одна и та же), а постоянная “с” зависит
от свойств второй жидкости.
Распад некоторых изотопов легких
элементов противоречит вышеприведенным рассуждениям. Однако это противоречие
кажущееся и обусловлено структурными особенностями этих изотопов. Рассмотрим
все эти случаи. Распад 4Be8 на две ![]() -частицы
был рассмотрен ранее и обусловлен тем, что при двух
-частицы
был рассмотрен ранее и обусловлен тем, что при двух ![]() -частицах
расщепление гравидинамического потока невозможно осуществить, поэтому поле остается
внутри
-частицах
расщепление гравидинамического потока невозможно осуществить, поэтому поле остается
внутри ![]() -частиц и они практически не взаимодействуют
друг с другом, за исключением электростатического отталкивания (аналогично
атомам инертных газов). Распад 2He5 на нейтрон и
-частиц и они практически не взаимодействуют
друг с другом, за исключением электростатического отталкивания (аналогично
атомам инертных газов). Распад 2He5 на нейтрон и ![]() -частицу
обусловлен тем, что это ядро очень далеко от оптимального состава (n/P=1,5,
а по формуле (12.1.13) должно быть n/P=0,94), поэтому ядро должно испускать
нейтрон и остается
-частицу
обусловлен тем, что это ядро очень далеко от оптимального состава (n/P=1,5,
а по формуле (12.1.13) должно быть n/P=0,94), поэтому ядро должно испускать
нейтрон и остается ![]() -частица. Распад 6C9:
-частица. Распад 6C9:
![]() ,
P, 2
,
P, 2![]() обусловлен тем, что это ядро
очень далеко от оптимального состава (n/P=0,5, а по формуле (12.1.13)
должно быть n/P=0,98), поэтому ядро должно испускать позитрон, а
появившийся из протона нейтрон завершает образование второй
обусловлен тем, что это ядро
очень далеко от оптимального состава (n/P=0,5, а по формуле (12.1.13)
должно быть n/P=0,98), поэтому ядро должно испускать позитрон, а
появившийся из протона нейтрон завершает образование второй ![]() -частицы. Образуется
комплекс 4Be8+P, который и распадается на протон и
две
-частицы. Образуется
комплекс 4Be8+P, который и распадается на протон и
две ![]() -частицы.
Распад 3Li6:
-частицы.
Распад 3Li6: ![]() , 2
, 2![]() обусловлен
также большим отклонением от оптимального состава ядра (n/P=1,7, а по
формуле (12.1.13) должно быть n/P=0,97), поэтому ядро должно испускать
электрон с образованием опять 4Be8. Распад: 5B8:
обусловлен
также большим отклонением от оптимального состава ядра (n/P=1,7, а по
формуле (12.1.13) должно быть n/P=0,97), поэтому ядро должно испускать
электрон с образованием опять 4Be8. Распад: 5B8:
![]() ,
2
,
2![]() также идет через 4Be8 (n/P=0,6, а надо 0,97).
В ряду изотопов с
также идет через 4Be8 (n/P=0,6, а надо 0,97).
В ряду изотопов с ![]()
![]() -распадом:
7N12, 11Na20, 13Al24,
17Cl32 все они имеют последовательно увеличивающееся
отклонение от оптимального состава в сторону избытка протонов, следовательно,
-распадом:
7N12, 11Na20, 13Al24,
17Cl32 все они имеют последовательно увеличивающееся
отклонение от оптимального состава в сторону избытка протонов, следовательно, ![]() -радиоактивны.
Кроме того, каждая
-радиоактивны.
Кроме того, каждая ![]() -частица
способна соединяться с другими имея, как минимум, три нуклона в соединительном
узле, поэтому у 7N12 вообще нет ни одной целой
-частица
способна соединяться с другими имея, как минимум, три нуклона в соединительном
узле, поэтому у 7N12 вообще нет ни одной целой ![]() -частицы,
а у 17Cl32 на 5 целых
-частицы,
а у 17Cl32 на 5 целых ![]() -частиц
приходится 4 нецелых (с тремя нуклонами), поэтому указанные изотопы имеют максимально
рыхлую структуру из всех возможных ядер, из-за чего
-частиц
приходится 4 нецелых (с тремя нуклонами), поэтому указанные изотопы имеют максимально
рыхлую структуру из всех возможных ядер, из-за чего ![]() -распад их
конкурирует с
-распад их
конкурирует с ![]() -распадом. Этими примерами исчерпываются
кажущиеся отклонения распадов некоторых изотопов от теории.
-распадом. Этими примерами исчерпываются
кажущиеся отклонения распадов некоторых изотопов от теории.
Из строения ядер, представленного в
начале этой главы и теории ![]() -распада
явствует принципиальная невозможность образования ядер из одних нейтронов или
ядер водорода, содержащих более двух нейтронов (тритий), т.к. нейтроны в этих
случаях некуда “прилепить”. “Хотя ядерное взаимодействие в синглетном состоянии
недостаточно велико, чтобы образовать бинейтрон, это не исключает возможности
образования связанной системы, состоящей из большого числа одних только
нейтронов - нейтронных ядер. Этот вопрос требует дальнейшего теоретического и
экспериментального изучения. Попытки обнаружить на опыте ядра из трех-четырех
нейтронов, а также ядра Н4, Н5,
Н6 не дали пока положительных результатов”. Физика микромира,
“Советская энциклопедия”, М., 1980, стр. 284. Для образования ядер из нейтронов
нужно огромное давление обусловленное гравитацией, что
происходит при коллапсе Вселенной.
-распада
явствует принципиальная невозможность образования ядер из одних нейтронов или
ядер водорода, содержащих более двух нейтронов (тритий), т.к. нейтроны в этих
случаях некуда “прилепить”. “Хотя ядерное взаимодействие в синглетном состоянии
недостаточно велико, чтобы образовать бинейтрон, это не исключает возможности
образования связанной системы, состоящей из большого числа одних только
нейтронов - нейтронных ядер. Этот вопрос требует дальнейшего теоретического и
экспериментального изучения. Попытки обнаружить на опыте ядра из трех-четырех
нейтронов, а также ядра Н4, Н5,
Н6 не дали пока положительных результатов”. Физика микромира,
“Советская энциклопедия”, М., 1980, стр. 284. Для образования ядер из нейтронов
нужно огромное давление обусловленное гравитацией, что
происходит при коллапсе Вселенной.
Но здесь имеется одно крайне
интересное возражение. Поскольку ![]() -гиперон
(см. фиг. 9.6.2.1) является “нейтроном”, в котором на орбите вокруг протона
находится не электрон, а
-гиперон
(см. фиг. 9.6.2.1) является “нейтроном”, в котором на орбите вокруг протона
находится не электрон, а ![]() -мезон, гравидинамическая связь которого с
протоном значительно прочнее, чем электрона, то возможно образование
“гиперонной альфа-частицы” в которой
-мезон, гравидинамическая связь которого с
протоном значительно прочнее, чем электрона, то возможно образование
“гиперонной альфа-частицы” в которой ![]() -гиперон занимает положение
второго протона. Состав этой частицы: протон, два нейтрона и
-гиперон занимает положение
второго протона. Состав этой частицы: протон, два нейтрона и ![]() -гиперон,
т.е. Н4. При этом связь двух протонов осуществляется
-гиперон,
т.е. Н4. При этом связь двух протонов осуществляется ![]() -мезоном
по типу одноэлектронной связи в молекулах (см. типы химической связи). Таким
образом, гипероны в ядре позволяют говорить о “молекулярной химии” ядра и
дальнейшие исследования в этой области приведут к интереснейшим результатам.
“Энергия связи гиперона в ядре трития очень мала - всего 0,06 Мэв, в изотопе
водорода
-мезоном
по типу одноэлектронной связи в молекулах (см. типы химической связи). Таким
образом, гипероны в ядре позволяют говорить о “молекулярной химии” ядра и
дальнейшие исследования в этой области приведут к интереснейшим результатам.
“Энергия связи гиперона в ядре трития очень мала - всего 0,06 Мэв, в изотопе
водорода ![]() она составляет 2 Мэв (изотоп водорода Н4, состоящий из одного протона и трех
нейтронов, в природе не существует)”. Физика микромира, “Советская
энциклопедия”, М., 1980, стр. 506.
она составляет 2 Мэв (изотоп водорода Н4, состоящий из одного протона и трех
нейтронов, в природе не существует)”. Физика микромира, “Советская
энциклопедия”, М., 1980, стр. 506.
Необходимо сделать одно критическое
замечание касающееся логической ошибки в известных теориях ![]() и
и ![]() -распада.
Распад ядер объясняют тем, что в результате распада образуются более устойчивые
ядра, т.е. процесс энергетически выгоден. Таким образом, движущей силой распада
фактически считают "знание" ядром своей будущей судьбы, чем оно,
якобы, и руководствуется. Очевидно, что причина распада лежит не вне, а внутри
ядра и самопроизвольное образование более устойчивого ядра является не
причиной, а следствием распада.
-распада.
Распад ядер объясняют тем, что в результате распада образуются более устойчивые
ядра, т.е. процесс энергетически выгоден. Таким образом, движущей силой распада
фактически считают "знание" ядром своей будущей судьбы, чем оно,
якобы, и руководствуется. Очевидно, что причина распада лежит не вне, а внутри
ядра и самопроизвольное образование более устойчивого ядра является не
причиной, а следствием распада.
Как известно, классические представления
не могут объяснить ![]() -распад,
т.к. излучаемая
-распад,
т.к. излучаемая ![]() -частица, например, у 92U238
имеет энергию равную 4,18 Мэв, которую она могла бы приобрести, двигаясь от
ядра с расстояния не менее 45 фм, а облучение ядра урана
-частица, например, у 92U238
имеет энергию равную 4,18 Мэв, которую она могла бы приобрести, двигаясь от
ядра с расстояния не менее 45 фм, а облучение ядра урана ![]() -частицами с
энергией 8,8 Мэв показывает рассеяние под действием кулоновских сил, т.е.
высота потенциального электростатического барьера составляет 8,8 Мэв, что
соответствует расстоянию от ядра 30 фм. Для объяснения этого
парадокса привлекается "туннельный" эффект (чисто волновое свойство
"частиц"), но если уж быть до конца последовательным, то
"туннельный" эффект, в принципе, отрицает стабильное существование
любых систем в микромире, начиная от атомов и кончая "элементарными"
частицами, если они из чего-нибудь состоят. Фактически - это отрицание
существования нашего мира в любых его формах. Если же учесть, что
"испаряющаяся" из ядра
-частицами с
энергией 8,8 Мэв показывает рассеяние под действием кулоновских сил, т.е.
высота потенциального электростатического барьера составляет 8,8 Мэв, что
соответствует расстоянию от ядра 30 фм. Для объяснения этого
парадокса привлекается "туннельный" эффект (чисто волновое свойство
"частиц"), но если уж быть до конца последовательным, то
"туннельный" эффект, в принципе, отрицает стабильное существование
любых систем в микромире, начиная от атомов и кончая "элементарными"
частицами, если они из чего-нибудь состоят. Фактически - это отрицание
существования нашего мира в любых его формах. Если же учесть, что
"испаряющаяся" из ядра ![]() -частица
должна получить кинетическую энергию вдоль оси винтовой линии и такую же
энергию по виткам винтовой линии (экспериментально мы определяем лишь энергию
поступательной составляющей, а тангенциальная составляющая не фиксируется).
Кроме того, ядро при отдаче получает энергию, как по оси, так и по виткам
винтовой линии и все это за счет электростатической энергии отталкивания. Если
учесть все это, то все становится на свои места без "туннельного"
эффекта.
-частица
должна получить кинетическую энергию вдоль оси винтовой линии и такую же
энергию по виткам винтовой линии (экспериментально мы определяем лишь энергию
поступательной составляющей, а тангенциальная составляющая не фиксируется).
Кроме того, ядро при отдаче получает энергию, как по оси, так и по виткам
винтовой линии и все это за счет электростатической энергии отталкивания. Если
учесть все это, то все становится на свои места без "туннельного"
эффекта.
“Прохождением частиц через потенциальный барьер объясняется целый ряд явлений: внешняя контактная разность потенциалов при соприкосновении разнородных проводников, холодная эмиссия электронов (испускание электронов с поверхности проводника при напряженности электрического поля вблизи этой поверхности свыше ~100 кэв/см), некоторые особенности ядерных реакций, a-распад ядер и т.д.”. Г.Е. Пустовалов, Атомная и ядерная физика, Изд. Московского университета, 1968, стр. 61. Выходит, официальная наука утверждает, что устойчивых образований в микромире принципиально не может быть. Возникает и другое противоречие: поскольку квантовая механика рассматривает частицу, как волну, которая отражается от двух стенок барьера, то часть “частицы” вернется обратно, часть застрянет внутри барьера, а часть пройдет через барьер. Так, где же будет сама частица? Ответ дан в главе 3.4.
Очевидно, что ядра радиоактивных
элементов, испускающих ![]() -излучение
с очень большим периодом полураспада выбрасывают
-излучение
с очень большим периодом полураспада выбрасывают ![]() -частицы с энергией, почти в точности соответствующей
глубине потенциальной ямы, в которой они находятся в ядре, т.е. их кинетическая
энергия на вершине потенциального барьера оказывается равной нулю. Энергия
-частицы с энергией, почти в точности соответствующей
глубине потенциальной ямы, в которой они находятся в ядре, т.е. их кинетическая
энергия на вершине потенциального барьера оказывается равной нулю. Энергия ![]() -частиц
излучаемых такими ядрами минимальна. Величина электростатической энергии:
-частиц
излучаемых такими ядрами минимальна. Величина электростатической энергии:
![]() (12.2.1).
(12.2.1).
Эта же энергия
расходуется на движение ядра отдачи и ![]() -частицы по винтовым
линиям:
-частицы по винтовым
линиям:
![]() (12.2.2).
(12.2.2).
Учитывая, что по закону сохранения количества движения:
![]() , откуда:
, откуда: ![]() (12.2.3)
(12.2.3)
и подставляя (12.2.3) в (12.2.2), найдем:
![]() (12.2.4).
(12.2.4).
Подставив (12.2.4) в (12.2.1), получим:
 (12.2.5).
(12.2.5).
Подставив в (12.2.5) значения констант, получим расчетную формулу:
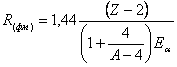 (
(![]() -Мэв)
(12.2.6).
-Мэв)
(12.2.6).
Расчет по формуле (12.2.6) дает величины R, указанные в таблице 12.2.1. Подставив эти значения R в (12.2.1), найдем величину потенциального барьера En также указанную в таблице.
Таблица 12.2.1.
|
Изотоп |
R(фм) |
|
En (Мэв) |
|
92U238 |
30,5 |
4,18 |
8,5 |
|
58Ce142 |
52,2 |
1,5 |
3,1 |
|
60Nd144 |
45,1 |
1,8 |
3,7 |
|
62Sm146 |
33,0 |
2,55 |
5,2 |
|
62Sm147 |
38,5 |
2,18 |
4,5 |
|
4Be8 |
28,8 |
0,05 |
0,2 |
|
|
|
|
|
|
Из таблицы видно совпадение для 92U238 экспериментальных и теоретических данных и несостоятельность "туннельного" эффекта. В связи с этим, надо учитывать то обстоятельство, что при поглощении ядром любой частицы, она вносит в ядро энергию, равную ее удвоенной поступательной энергии. Поэтому, положительно заряженная поступательно движущаяся частица, имеющая энергию, примерно, в два раза меньше потенциального барьера беспрепятственно попадает в ядро, демонстрируя снова "туннельный" эффект. При этом собственное вращение частицы также передается ядру в целом, т.к. частица внутри ядра вращаться не может. Поэтому вышеприведенные расчеты требуют уточнения, усиливающего "туннельный" эффект.
Вышеприведенные расчеты позволяют, не зная аналитического вида кривой
гравидинамического притяжения, построить примерный график изменения
потенциальной энергии в зависимости от расстояния от ядра. Такой график
приведен на фигуре 12.2.1 для 92U238 при
взаимодействии с ![]() -частицей.
-частицей.
Из таблицы 12.2.1 и фигуры 12.2.1 мы видим, что, несмотря на различную высоту
потенциального барьера для разных изотопов и разную энергию излучаемых ![]() -частиц,
изменяющуюся на два порядка, "кулоновский радиус" потенциального
барьера изменяется слабо в пределах 30-50 фм. О радиусе действия ядерных сил,
естественно, говорить не приходится, кроме того, что гравидинамическое
взаимодействие спадает с расстоянием от ядра гораздо круче кулоновского. Для
рассматриваемого случая взаимодействия
-частиц,
изменяющуюся на два порядка, "кулоновский радиус" потенциального
барьера изменяется слабо в пределах 30-50 фм. О радиусе действия ядерных сил,
естественно, говорить не приходится, кроме того, что гравидинамическое
взаимодействие спадает с расстоянием от ядра гораздо круче кулоновского. Для
рассматриваемого случая взаимодействия ![]() -частицы с ядром, радиусом
действия ядерных сил условно можно считать расстояние до вершины потенциального
барьера.
-частицы с ядром, радиусом
действия ядерных сил условно можно считать расстояние до вершины потенциального
барьера.
Из официальной теории туннельного эффекта известно, что при ![]()
![]() 0 вероятность
прохождения через барьер обращается в нуль. Физический смысл этого с точки
зрения новой физики состоит в том, что при
0 вероятность
прохождения через барьер обращается в нуль. Физический смысл этого с точки
зрения новой физики состоит в том, что при ![]()
![]() 0 частица движется
прямолинейно и является "классической". Чем больше момент
количества движения тем больше радиус винтовой
траектории частицы и в большей мере проявляются ее "волновые"
свойства. Поэтому частица оказывается за барьером, который должен был бы ее
задержать, если бы она двигалась прямолинейно. Таким же образом, если ось
винтовой траектории направлена мимо барьера и классическая частица не отразится
от барьера, частица, движущаяся по винтовой траектории, может попасть в барьер
(так называемое надбарьерное отражение).
0 частица движется
прямолинейно и является "классической". Чем больше момент
количества движения тем больше радиус винтовой
траектории частицы и в большей мере проявляются ее "волновые"
свойства. Поэтому частица оказывается за барьером, который должен был бы ее
задержать, если бы она двигалась прямолинейно. Таким же образом, если ось
винтовой траектории направлена мимо барьера и классическая частица не отразится
от барьера, частица, движущаяся по винтовой траектории, может попасть в барьер
(так называемое надбарьерное отражение).
12.3. Связь строения со свойствами легких ядер
Учитывая энергию связи в ядрах (Мэв): 1D1=2,20; 1T3=8,49; 2He3=7,72; 2He4=28,3 и энергию отталкивания протонов в ядре (на один протон) 0,77 Мэв, можно изобразить схемы соединения нуклонов в ядре с соответствующим выигрышем энергии при этом соединении. Присоединяемая частица показана в эллипсе. Нейтроны изображены двойной стрелкой, а протоны – одинарной. Направление стрелки показывает направление вращения протона.
Теперь можно рассмотреть связь строения ядер и их свойств, двигаясь в сторону ядра 6С12, более сложные ядра нет смысла обсуждать, принципы для всех ядер одинаковы. Два протона или два нейтрона не могут образовать устойчивое ядро. Причина в том, что для обеспечения гравидинамического притяжения «рамок с током», составляющие протонов должны двигаться параллельно друг другу, но тогда они отталкиваются за счет гравидинамического аналога силы Лоренца и наоборот. В дейтроне отталкивание за счет гравидинамического аналога силы Лоренца компенсирует электрон нейтрона, который занимает положение между протонами и таким образом связывает их, поэтому связь нуклонов в дейтроне небольшая. Хотя образование трития немного более выгодно, чем образование 2He3, но гравидинамическая связь одинакова у этих частиц.
|
Соединение |
Выигрыш энергии, Мэв |
Примечание |
|
|
2,2 |
Образование дейтрона 2,2
Мэв |
|
|
5,52 |
Образование 2He3
7,72 Мэв |
|
|
6,29 |
Образование трития 8,49 Мэв |
|
|
19,8 |
Образование 2He4 28,3
Мэв |
|
|
20,58 |
Образование 2He4 28,3
Мэв |
|
|
-0,77 |
Отталкивание ближайших протонов |
Поскольку избыточные нейтроны склонны превращаться в протоны, то
ядро трития не устойчиво: 1T3![]() 2He3+e-+
2He3+e-+![]() (далее нейтрино в
реакциях указывать не будем). Замыкание гравидинамического поля внутри тора из
четырех нуклонов
(далее нейтрино в
реакциях указывать не будем). Замыкание гравидинамического поля внутри тора из
четырех нуклонов ![]() -частицы
настолько выгодно, что даже если в ядро 2He3 силком поместить еще
один протон в место помеченной темной точкой, то он предпочтет превратиться в
нейтрон, чем удалиться (1): 2He3+1H1
-частицы
настолько выгодно, что даже если в ядро 2He3 силком поместить еще
один протон в место помеченной темной точкой, то он предпочтет превратиться в
нейтрон, чем удалиться (1): 2He3+1H1![]() 2He4+e+. В
2He4+e+. В ![]() -частице
гравидинамическое поле наружу практически не выходит. Если дополнительные
нуклоны не смогут расщепить гравидинамический поток, чтобы вывести часть его из
-частице
гравидинамическое поле наружу практически не выходит. Если дополнительные
нуклоны не смогут расщепить гравидинамический поток, чтобы вывести часть его из
![]() -частицы
наружу, то такие ядра окажутся не стабильными.
-частицы
наружу, то такие ядра окажутся не стабильными.
![]()
|
|
|
|
|
|
Ядро 2He5
(2) неустойчиво: 2He5![]() 2He4+n. Ядро 2He6 (3) тоже не
устойчиво, но появляется возможность расщепить гравидинамический поток путем
превращения одного нейтрона в протон и встраивания его в место, помеченное
точкой. В результате образуется ядро 3Li6 (4): 2He6
2He4+n. Ядро 2He6 (3) тоже не
устойчиво, но появляется возможность расщепить гравидинамический поток путем
превращения одного нейтрона в протон и встраивания его в место, помеченное
точкой. В результате образуется ядро 3Li6 (4): 2He6![]() 3Li6+e-. Ядро 2He7 (5) имеет
такой большой избыток нейтронов, что испускает один из них: 2He7
3Li6+e-. Ядро 2He7 (5) имеет
такой большой избыток нейтронов, что испускает один из них: 2He7![]() 2He6+n. Дальнейшее поведение 2He6 мы
обсудили выше. Ядро 2He8 (6) еще менее устойчиво и может испустить
нейтрон, превратившись в 2He7 или один нейтрон
превращается в протон, который встраивается в место, помеченное точкой: 2He8
2He6+n. Дальнейшее поведение 2He6 мы
обсудили выше. Ядро 2He8 (6) еще менее устойчиво и может испустить
нейтрон, превратившись в 2He7 или один нейтрон
превращается в протон, который встраивается в место, помеченное точкой: 2He8![]() 3Li8+e-. Ядро 3Li8 (7) также
неустойчиво т.к. здесь очень выгодно достроить вторую
3Li8+e-. Ядро 3Li8 (7) также
неустойчиво т.к. здесь очень выгодно достроить вторую ![]() -частицу, превратив нейтрон
в протон и разместить его в место, помеченное точкой. В результате образуется 4Be8 (8),
который крайне неустойчив, т.к. гравидинамические потоки вновь замыкаются
внутри
-частицу, превратив нейтрон
в протон и разместить его в место, помеченное точкой. В результате образуется 4Be8 (8),
который крайне неустойчив, т.к. гравидинамические потоки вновь замыкаются
внутри ![]() -частиц
и не связывают их между собой: 4Be8
-частиц
и не связывают их между собой: 4Be8![]() 22He4. Это
свойство ядра Be8
выгодно использовать в экзотермических ядерных реакциях. Ядро 3Li5 (9), как
видно из рисунка не может быть устойчивым и распадается на протон и
22He4. Это
свойство ядра Be8
выгодно использовать в экзотермических ядерных реакциях. Ядро 3Li5 (9), как
видно из рисунка не может быть устойчивым и распадается на протон и ![]() -частицу:
3Li5
-частицу:
3Li5![]() 2He4+1H1. Ядра 3Li6 (4) и 3Li7 (10)
устойчивы т.к. расшепление гравидинамического потока обеспечено.
2He4+1H1. Ядра 3Li6 (4) и 3Li7 (10)
устойчивы т.к. расшепление гравидинамического потока обеспечено.
|
|
|
|
|
|
Из рисунков 4 и 10 видно стремление 3Li6 принять дейтрон, а 3Li7 принять
или нейтрон, превращающийся в протон, или протон. В результате оба ядра
образуют неустойчивый 4Be8. В ядре 4Be6 (11)
удержать два протона у ![]() -частицы
нет возможности, поэтому оно распадается: 4Be6
-частицы
нет возможности, поэтому оно распадается: 4Be6![]() 2He4+21H1. Ядру 4Be7 выгодно в
положение, отмеченное точкой, приобрести нейтрон, поэтому проще всего это
сделать превращением слабо связанного протона в нейтрон в результате захвата
ближайшего к ядру электрона: 4Be7
2He4+21H1. Ядру 4Be7 выгодно в
положение, отмеченное точкой, приобрести нейтрон, поэтому проще всего это
сделать превращением слабо связанного протона в нейтрон в результате захвата
ближайшего к ядру электрона: 4Be7![]() 3Li7+e+. 4Be9 (13)
является единственным устойчивым изотопом бериллия, в
нем две
3Li7+e+. 4Be9 (13)
является единственным устойчивым изотопом бериллия, в
нем две ![]() -частицы дополнительно связаны нейтроном.
Ядро 4Be10
(14) было бы устойчиво, если бы не появилась возможность превратить один из
нейтронов в протон, вновь расщепить гравидинамический поток
-частицы дополнительно связаны нейтроном.
Ядро 4Be10
(14) было бы устойчиво, если бы не появилась возможность превратить один из
нейтронов в протон, вновь расщепить гравидинамический поток ![]() -частицы, и сформировать
таким образом еще более устойчивое ядро 5B10 (15) в результате
длительного процесса: 4Be10
-частицы, и сформировать
таким образом еще более устойчивое ядро 5B10 (15) в результате
длительного процесса: 4Be10![]() 5B10+e-.
5B10+e-.
|
|
|
|
|
|
Ядро 5B7
(16) не может быть устойчивым, т.к. к единственной ![]() -частице «прилеплены» три
протона очень слабо с ней связанные, поэтому ядро распадается: 5B7
-частице «прилеплены» три
протона очень слабо с ней связанные, поэтому ядро распадается: 5B7![]() 2He4+31H1. Ядро 5B8 (17)
обеспечивает расщепление гравидинамического потока
2He4+31H1. Ядро 5B8 (17)
обеспечивает расщепление гравидинамического потока ![]() -частицы и, таким образом
создает условия для образования второй
-частицы и, таким образом
создает условия для образования второй ![]() -частицы. Слабо связанный
протон превращается в нейтрон в результате e-захвата и встраивается в место,
отмеченное точкой с образованием 4Be8. Ядро 5B9 (18)
представляет собой слабо связанную систему двух
-частицы. Слабо связанный
протон превращается в нейтрон в результате e-захвата и встраивается в место,
отмеченное точкой с образованием 4Be8. Ядро 5B9 (18)
представляет собой слабо связанную систему двух ![]() -частиц и протона, которая
разваливается на компоненты. 5B11 (19) является самым
распространенным устойчивым изотопом бора, т.к. в нем обеспечено повторное
расщепление гравидинамического потока
-частиц и протона, которая
разваливается на компоненты. 5B11 (19) является самым
распространенным устойчивым изотопом бора, т.к. в нем обеспечено повторное
расщепление гравидинамического потока ![]() -частицы, что создает
условия для построения третьей
-частицы, что создает
условия для построения третьей ![]() -частицы в ядре. Очевидно, что ядро 5B11 с большим
желанием примет протон или даже нейтрон, который превратится в протон, чтобы
достроить третью
-частицы в ядре. Очевидно, что ядро 5B11 с большим
желанием примет протон или даже нейтрон, который превратится в протон, чтобы
достроить третью ![]() -частицу
с образованием 6С12 (20). Хотя изотоп углерода 6С12
имеет очень прочное и устойчивое ядро, но в реакции 5B11+n
-частицу
с образованием 6С12 (20). Хотя изотоп углерода 6С12
имеет очень прочное и устойчивое ядро, но в реакции 5B11+n![]() 6С12+e- выделяется
много энергии, которой достаточно, чтобы так возбудить ядро 6С12,
что оно разваливается на отдельные
6С12+e- выделяется
много энергии, которой достаточно, чтобы так возбудить ядро 6С12,
что оно разваливается на отдельные ![]() -частицы. Для практического
использования перспективна «чистая» и дешевая реакция (можно пользоваться
природными материалами не разделяя изотопы): 5B11+1H1
-частицы. Для практического
использования перспективна «чистая» и дешевая реакция (можно пользоваться
природными материалами не разделяя изотопы): 5B11+1H1![]() 32He4 Q
32He4 Q![]() 8,6 Мэв. Из анализа
свойств ядер можно сделать вывод, что самый выгодный процесс – достройка до
полной
8,6 Мэв. Из анализа
свойств ядер можно сделать вывод, что самый выгодный процесс – достройка до
полной ![]() -частицы,
при этом если для этого нужен протон, а в наличии есть нейтрон, то он
превращается в протон. Если нужен нейтрон, а в наличии есть протон, то он
превращается в нейтрон. На втором месте по эффективности – достройка до
фрагмента ядра «тритий» (pnn)
присоединением нейтрона к «дейтерию» (pn). При этом фрагмент ядра (ppn) превращается во фрагмент (pnn). Глядя на
изображения ядер легко представить себе механизм любой ядерной реакции и
примерно оценить ее тепловой эффект. Магнитные моменты ядер также можно приблизительно
предсказать по изображению ядер. Точные значения связаны с расчетами,
выходящими за тематику этой главы. Так, например магнитный момент дейтерия
равен сумме магнитных моментов протона и нейтрона (небольшая разница связана со
смещением электрона нейтрона в сторону протона). Магнитный момент He3 определяется
моментом нейтрона, т.к. магнитные моменты протонов скомпенсированы. Магнитный
момент He4
равен нулю, т.к. магнитные моменты нуклонов полностью скомпесированы или можно
считать, что два магнитных момента «дейтронов» взаимно противоположны. У Li6 магнитный
момент определяется «дейтроном», у Li7 – «тритоном», у Be9 нейтроном и т.д. Если
в кристаллической решетке ядра, количество нейтронов, вращающихся в одном
направлении, равно количеству нейтронов, вращающихся в противоположном
направлении, и то же касается протонов, то магнитный момент таких ядер равен
нулю.
-частицы,
при этом если для этого нужен протон, а в наличии есть нейтрон, то он
превращается в протон. Если нужен нейтрон, а в наличии есть протон, то он
превращается в нейтрон. На втором месте по эффективности – достройка до
фрагмента ядра «тритий» (pnn)
присоединением нейтрона к «дейтерию» (pn). При этом фрагмент ядра (ppn) превращается во фрагмент (pnn). Глядя на
изображения ядер легко представить себе механизм любой ядерной реакции и
примерно оценить ее тепловой эффект. Магнитные моменты ядер также можно приблизительно
предсказать по изображению ядер. Точные значения связаны с расчетами,
выходящими за тематику этой главы. Так, например магнитный момент дейтерия
равен сумме магнитных моментов протона и нейтрона (небольшая разница связана со
смещением электрона нейтрона в сторону протона). Магнитный момент He3 определяется
моментом нейтрона, т.к. магнитные моменты протонов скомпенсированы. Магнитный
момент He4
равен нулю, т.к. магнитные моменты нуклонов полностью скомпесированы или можно
считать, что два магнитных момента «дейтронов» взаимно противоположны. У Li6 магнитный
момент определяется «дейтроном», у Li7 – «тритоном», у Be9 нейтроном и т.д. Если
в кристаллической решетке ядра, количество нейтронов, вращающихся в одном
направлении, равно количеству нейтронов, вращающихся в противоположном
направлении, и то же касается протонов, то магнитный момент таких ядер равен
нулю.
Из анализа этой главы можно сделать следующие выводы. 1. Нуклоны в ядрах плотно упакованы, что подтверждается экспериментальными данными. Поэтому в ядре нет возможности образовать какие-либо оболочки, в которых двигаются нуклоны. 2. Ядра представляют собой кристаллическую решетку из альфа-частиц. В этих частицах протоны и нейтроны спарены и представляют собой бозоны с точки зрения официальной физики. Поэтому принцип запрета Паули к ядрам не применим. Я вообще его не признаю т.к. он приводит к максимуму энтропии, который уже невозможно превысить.
В связи с этим официальная физика вынуждена отрицать существование альфа частиц в ядре, вопреки очевидным экспериментальным данным.
1. Какая температура достигается при коллапсе космических тел.
При гравитационном сжатии материала гравитационная энергия равна:
![]() (12.4.1),
(12.4.1),
где G – гравитационная постоянная, M – масса космического тела, R – его радиус.
Очевидно, что вся гравитационная энергия превращается в теплоту при адиабатическом сжатии:
![]() (12.4.2),
(12.4.2),
где c – удельная теплоемкость
(для разных материалов около 1 дж/г×град), ![]() T – разность конечной и начальной
температуры материала.
T – разность конечной и начальной
температуры материала.
Приравнивая (12.4.1) и (12.4.2), найдем:
![]() (12.4.3).
(12.4.3).
Подставляя в (12.4.3) астрономические данные, найдем: для Солнца ![]() T=19×106 0K, Для Юпитера 177000 0K, для Земли 6250 0K, для Луны 282 0K.
T=19×106 0K, Для Юпитера 177000 0K, для Земли 6250 0K, для Луны 282 0K.
Поскольку после образования этих космических тел у них была возможность в течение нескольких миллиардов лет остывать за счет излучения, то полученные данные правильнее отнести к центральной области указанных тел. Здесь нужно учитывать, что кроме потери энергии за счет излучения, эти тела и приобретают ее за счет метеоритной и кометной бомбардировки. Компенсацию потерь энергии Солнца за счет термоядерного синтеза здесь рассматривать не имеет смысла.
Выясним условия образования нейтронной звезды за счет коллапса в предположении, что энергия за счет ядерных реакций полностью исчерпана и холодная звезда с массой Солнца сжимается от плотности примерно равной 1 г/см3 до почти ядерной плотности 1013 г/см3. При этих условиях (12.4.3) даст увеличение температуры на 3,67×1012 0K. При этой температуре любая частица будет обладать энергией 474 Мэв, что с большим запасом достаточно для «расплавления» любых ядер и образования нейтронного тела с очень высокой температурой. Поэтому свехядро способно сформироваться внутри или снаружи этого тела после длительного периода остывания и дальнейшего уплотнения, пока энергия частиц не снизится до 7 Мэв (5,4×1010 0K).
2. Прямое образование дейтерия, трития и 2He3.
В главе 12.2 было показано, что максимальная высота потенциального барьера при взаимодействии альфа-частиц с различными ядрами расположена на расстоянии, примерно, 30 fm (30×10-13 см) между взаимодействующими частицами и практически не зависит от массы ядер. Потенциальная энергия двух протонов на расстоянии r составляет e2/r, а их энергия, связанная с тепловым движением при встречном столкновении составит 10kT. В главе о фотонах показано, что полная энергия частицы, движущейся по винтовой траектории, составит 5kT (имеет 10 степеней свободы).
Тогда:
![]() (12.4.4).
(12.4.4).
Подставляя в (12.4.4) вышеприведенное значение r и мировые постоянные, найдем T=55,6×106
0K. Таким образом, при этой температуре дейтерий образуется без проблем
при слиянии двух протонов: 1H1+1H1=1D2+e++![]() .
Образование трития и 2He3 еще проще, т.к. нейтрон в дейтерии
способствует реакциям: 1D2+1H1=1T3+e++
.
Образование трития и 2He3 еще проще, т.к. нейтрон в дейтерии
способствует реакциям: 1D2+1H1=1T3+e++![]() и 1D2+1H1=2He3+
и 1D2+1H1=2He3+![]() .
Протекающие в дальнейшем экзотермические реакции в этой смеси не только
покрывают затраты энергии, но и значительно превышают их: 1H1+1T3=2He4+Q, 1D2+1D2=2He3+0n1+Q, 1D2+1T3=2He4+0n1+Q, 2He3+0n1=2He4+Q.
.
Протекающие в дальнейшем экзотермические реакции в этой смеси не только
покрывают затраты энергии, но и значительно превышают их: 1H1+1T3=2He4+Q, 1D2+1D2=2He3+0n1+Q, 1D2+1T3=2He4+0n1+Q, 2He3+0n1=2He4+Q.
Нейтроны в составе ядер не только отодвигают потенциальный барьер дальше 30 fm, но и значительно уменьшают его величину за счет дополнительного гравидинамического притяжения между сталкивающимися частицами. Это видно не только для двух изотопов Sm146 и Sm147 в таблице 12.2.1 главы 12.2, но также из экспериментальных данных ядерной физики. Например, реакция 1D2+1T3 идет уже при температуре в 6 раз ниже (примерно, 106 0K) и может быть возбуждена кумулятивным взрывом обычного взрывчатого вещества («чистая» водородная бомба).
Сравнивая температуры недр космических тел с температурами прямого термоядерного синтеза (не учитывая реакций с нейтронами и каталитических циклов) можно сделать следующие выводы. Для космических тел с массой Солнца термоядерный синтез легко осуществим, т.к. требуемая для этого температура всего в 3 раза больше температуры, достигаемой за счет коллапса. В максвелловском распределении частиц по энергиям вполне достаточно таких быстрых частиц. Поэтому быстрый разогрев недр за счет термоядерного синтеза приводит к тепловому взрыву звезды и сбрасыванию оболочки в космическое пространство. Для космических тел с массой Юпитера температура внутри в 300 раз меньше необходимой, поэтому только некоторые особо быстрые частицы способны к прямому ядерному синтезу. Для таких космических тел невозможна скорая вспышка с образованием звезды при достижении определенного радиуса при коллапсе, т.к. такой радиус недостижим за счет противодействия сжатого газа. Остается только эволюционный путь постепенного разогрева недр за счет вяло протекающих реакций синтеза с накоплением дейтерия. Как только дейтерия накопится достаточно (тритий радиоактивен, поэтому не накапливается в достаточном количестве), он способен начать реакцию с образованием нейтронов, которые резко ускорят процесс разогрева недр до температуры вспышки новой звезды. Обнаружение в излучении Юпитера нейтрино подтвердит, что соответствующие реакции уже пошли. Описанная медленная эволюция в звезду – судьба всех планет юпитерной группы, интенсивно увеличивающих свою массу за счет захвата. Планетам земной группы подобная участь не грозит из-за низкой температуры недр и отсутствия свободных протонов. Редкие акты поглощения космических нейтрино с очень большой энергией и затухающие процессы радиоактивного распада в недрах не могут компенсировать постепенного охлаждения этих планет.
3. Ядерные реакции с нейтронами.
Для ядерных реакций с нейтронами нет необходимости в высоких
температурах, т.к. нейтрон способен свободно соединяться с протонами или
проникать в ядро. Какие существуют природные условия для «холодного»
образования нейтронов? Протон может превращаться в нейтрон только внутри ядра
атома, обладающего избытком протонов по сравнению с равновесным их количеством.
Для практического получения энергии этот процесс не подходит. Однако при
выгорании водорода в звездах и их охлаждении ничто не препятствует их
повторному коллапсу. Если масса бывшей звезды невелика, то она остывает совсем
и пополняет население «темной материи». Если масса большая, то коллапс идет до
плотности, при которой происходит нейтронизация вещества за счет потери
электронами момента импульса ![]() . При этом они соединяются с протонами с
образованием нейтронов. При накоплении достаточного количества нейтронов
происходит новая вспышка звезды за счет выделения тепла в ядерных реакциях с
участием нейтронов. В результате этих реакций, в конце концов, образуется
железо и никель. Ядерные реакции вновь прекращаются, звезда вновь остывает. Если ее масса недостаточна для глобальной нейтронизации вещества,
то остывшая «железная» звезда пополнит «темную материю». Если масса
остается огромной, то новый коллапс неизбежен с образованием нейтронной звезды.
Нейтронная звезда принципиально неустойчива, при достижении ядерной плотности и
достаточном охлаждении внутри ее образуется сверхядро, что приводит на этот раз
к столь грандиозному взрыву, что все вещество рассеивается в пространстве,
происходит «Большой Взрыв» в малом масштабе и образование кроме легких, тяжелых
и сверхтяжелых элементов (осколков сверхядра).
. При этом они соединяются с протонами с
образованием нейтронов. При накоплении достаточного количества нейтронов
происходит новая вспышка звезды за счет выделения тепла в ядерных реакциях с
участием нейтронов. В результате этих реакций, в конце концов, образуется
железо и никель. Ядерные реакции вновь прекращаются, звезда вновь остывает. Если ее масса недостаточна для глобальной нейтронизации вещества,
то остывшая «железная» звезда пополнит «темную материю». Если масса
остается огромной, то новый коллапс неизбежен с образованием нейтронной звезды.
Нейтронная звезда принципиально неустойчива, при достижении ядерной плотности и
достаточном охлаждении внутри ее образуется сверхядро, что приводит на этот раз
к столь грандиозному взрыву, что все вещество рассеивается в пространстве,
происходит «Большой Взрыв» в малом масштабе и образование кроме легких, тяжелых
и сверхтяжелых элементов (осколков сверхядра).
В космическом пространстве вполне возможно длительное существование «холодных» электронов, которые потеряли момент импульса, передав его фотонам реликтового излучения или другим частицам. При этом электроны становятся «сверхпроводящими» т.к. окружающая температура соответствует 2,70 K и способны с протонами формировать «миниводород» - нейтроны.
4. Механизм прямого ядерного синтеза на примере образования дейтерия.
Когда протон окажется на вершине потенциального барьера взаимодействия,
он начинает «падать» в потенциальную яму гравидинамического притяжения к
другому протону. Процесс аналогичен «падению» электрона к протону при
образовании атома водорода. При этом избыточная энергия, которую необходимо
рассеять, чтобы завершить процесс, теряется не за счет излучения фотонов, а за
счет образования пары электрон-позитрон и пары нейтрино-антинейтрино. Последняя
пара является результатом распада фотона в мощном электрическом и
гравидинамическом поле двух протонов. Электрон, не имея момента импульса ![]() , и
антинейтрино соединяются с протоном, образуя «миниводород» – нейтрон, задолго
до достижения дна потенциальной ямы (иначе ее невозможно достичь) в которой
оказывается уже нейтрон. В целом, мы будем наблюдать следующую реакцию: 1H1+1H1=1D2+e++
, и
антинейтрино соединяются с протоном, образуя «миниводород» – нейтрон, задолго
до достижения дна потенциальной ямы (иначе ее невозможно достичь) в которой
оказывается уже нейтрон. В целом, мы будем наблюдать следующую реакцию: 1H1+1H1=1D2+e++![]() .
.
12.4.1. Термоядерный синтез на кухне
В детстве моей любимой, но опасной игрушкой был «поджиг». Он представляет собой Г-образно согнутую металлическую трубку, внутрь которой накрошены спичечные головки, в трубку вставлен Г-образно согнутый гвоздь под углом к оси трубки, который стянут резинкой с загибом трубки. Если нажать на резинку, то под ее действием гвоздь ударяет по горючему материалу в трубке и происходит детонация с оглушительным взрывом. На фигуре 12.4.1.1 представлено устройство для термоядерного синтеза, основанное на точно таком же принципе.
Цифрами на фигуре 12.4.1.1 обозначены: 1 – матрица, 2 – пуансон, 3 – шток, 4 – боек, 5 – котел, 6 – вода в котел, 7 – пар в турбину.
|
|
|
|
|
|
На дно конусной матрицы помещается маленький кристаллик Li6D (гидрида легкого изотопа лития в соединении с дейтерием) массой 0,1 мг. Наконечник 2 штока 3 имеет немного меньший раствор конуса, чем матрица и способен соприкасаться с ней только вершиной конуса. По штоку ударяет боек 4×, массой 10 кг со скоростью 40 м/сек. Матрица, пуансон и шток расположены внутри котла 5, в который поступает вода через патрубок 6 и отводится пар в турбину через патрубок 7.
В момент удара бойка по штоку, кинетическая энергия бойка превращается в тепло на вершине конуса пуансона.
![]() (12.4.1.1),
(12.4.1.1),
где M – масса бойка, V – скорость бойка, c – теплоемкость гидрида лития (~3,15 дж/г×град), m – масса гидрида лития.
Подставляя указанные значения в (12.4.1.1), получим ![]() T=25×106 0K, что соответствует
температуре внутри звезд. При такой температуре легко протекает реакция: Li6+D
T=25×106 0K, что соответствует
температуре внутри звезд. При такой температуре легко протекает реакция: Li6+D![]() 2He4+22Мэв.
Поскольку изотоп Li6
содержится в количестве всего 7% в природной смести изотопов лития, а дейтерий
чуть более 0,01%, то получение этих изотопов в чистом виде затруднительно.
Описанная установка позволяет осуществить термоядерный синтез с гидридом лития Li7H по схеме: Li7+P
2He4+22Мэв.
Поскольку изотоп Li6
содержится в количестве всего 7% в природной смести изотопов лития, а дейтерий
чуть более 0,01%, то получение этих изотопов в чистом виде затруднительно.
Описанная установка позволяет осуществить термоядерный синтез с гидридом лития Li7H по схеме: Li7+P![]() 2He4+
2He4+![]() . В этом
случае можно использовать природные материалы без трудоемкого разделения
изотопов, хотя процесс перестает быть «чистым». При описанном минитермоядерном
взрыве выделится 7,36 квт×час
энергии, которой достаточно, чтобы нагреть 63 л воды от 0 до 1000.
Мощность взрыва окажется не менее 30 млн. кВт. Шток, матрицу и пуансон придется
каждый раз заменять. Не сомневаюсь, что дотошные изобретатели автоматизируют
эту установку по принципам автоматического оружия. Из формулы (12.4.1.1) видно,
что увеличением массы бойка и его скорости можно достичь практически любые
желаемые температуры.
. В этом
случае можно использовать природные материалы без трудоемкого разделения
изотопов, хотя процесс перестает быть «чистым». При описанном минитермоядерном
взрыве выделится 7,36 квт×час
энергии, которой достаточно, чтобы нагреть 63 л воды от 0 до 1000.
Мощность взрыва окажется не менее 30 млн. кВт. Шток, матрицу и пуансон придется
каждый раз заменять. Не сомневаюсь, что дотошные изобретатели автоматизируют
эту установку по принципам автоматического оружия. Из формулы (12.4.1.1) видно,
что увеличением массы бойка и его скорости можно достичь практически любые
желаемые температуры.
12.4.2. Термоядерный синтез в промышленности
Описанный выше способ термоядерного синтеза можно сделать непрерывным, если обстреливать твердую массивную мишень, закрепленную в стенке котла специальными пулями или снарядами, устроенными по вышеизложенному принципу (фиг. 12.4.1.1). Отходы сваливаются вниз в бункер и удаляются. На фигуре 12.4.2.1:
|
|
|
|
|
|
1 – пуля, 2 – пуансон, 3 – матрица с кристалликом гидрида лития. В таком
способе легко достичь намного более высоких температур, т.к. при ударе о препятствие
вся кинетическая энергия пули прикладывается через пуансон к матрице, жестко
связанной с пулей. Подобное устройство может быть использовано для
термоядерного синтеза по реакции: D2+T3![]() He4+n+17,6
Мэв. Для этого пуансон представляет собой поршень, а матрица – цилиндр емкостью
0,01 мл, заполненный смесью дейтерия и трития. Реакция идет в благоприятных
условиях очень высокого давления, если пунсон плоский, а матрица выполнена со
сминаемой стенкой. Например, матрица может быть выполнена в
виде полого герметичного металлического конуса диаметром у основания 3
мм, заполненного водородом. Конус основанием опирается на плоскость, а плоский
пуансон ударяет по вершине конуса. Во время удара конус сминается, сохраняя
герметичность, температура внутри достигает десятков миллионов градусов, а
давление около миллиона атмосфер. Поэтому ударный термоядерный синтез
представляется наиболее перспективным для получения энергии в отличие от других
способов, имеющих незначительный КПД.
He4+n+17,6
Мэв. Для этого пуансон представляет собой поршень, а матрица – цилиндр емкостью
0,01 мл, заполненный смесью дейтерия и трития. Реакция идет в благоприятных
условиях очень высокого давления, если пунсон плоский, а матрица выполнена со
сминаемой стенкой. Например, матрица может быть выполнена в
виде полого герметичного металлического конуса диаметром у основания 3
мм, заполненного водородом. Конус основанием опирается на плоскость, а плоский
пуансон ударяет по вершине конуса. Во время удара конус сминается, сохраняя
герметичность, температура внутри достигает десятков миллионов градусов, а
давление около миллиона атмосфер. Поэтому ударный термоядерный синтез
представляется наиболее перспективным для получения энергии в отличие от других
способов, имеющих незначительный КПД.
В связи с этим интересно исследовать аномалии изотопного состава вещества в крупных кратерах при падении метеоритов.
Более совершенная конструкция показана на фигуре 12.4.2.2.
1 – тело пули, 2 – сминаемый герметичный наконечник заполненный смесью дейтерия и трития, 3 – детонатор из гремучей ртути.
При попадании в твердую мишень к ударному возбуждению термоядерной реакции прибавляется действие от взрыва детонатора и кумулятивной газовой струи в направлении наружного конца наконечника. Это гарантирует успешное завершение процесса.
|
|
|
|
|
|
Можно предложить еще один оригинальный способ промышленного получения ядерной
энергии синтеза. Если столкнутся два орбитальных электрона двух атомов
атомарного водорода, то они потеряют свои моменты импульсов и «упадут» на
протоны, в результате появятся два нейтрона. Этот процесс будет сопровождаться
гамма-излучением. Дальнейшие экзотермические реакции с участием нейтронов в
среде водорода протекают без затруднений. Для подобного генерирования нейтронов
столкновением орбитальных электронов не нужна высокая температура, но
необходимо высокое давление, чтобы столкновение орбитальных электронов при
хаотическом движении атомов стало хоть сколько-нибудь заметным. По-видимому,
подобный процесс ядерного синтеза нейтронов и далее дейтерия и трития
происходит внутри Юпитера, но он лимитируется скоростью генерирования нейтронов поскольку вероятность эффективного столкновения
орбитальных электронов при их случайном взаимном расположении крайне мала.
|
|
|
|
|
|
Очевидно, что для промышленного генерирования нейтронов из атомарного водорода необходимо резко увеличить вероятность столкновения орбитальных электронов. Здесь следует уточнить, что под столкновением электронов понимается не их непосредственный контакт а только электростатическое взаимодействие, приводящее к потере орбитального момента импульса. Очевидно, что столкнуть таким образом свободные электроны практически невозможно, т.к. они займут расходящиеся траектории задолго до «столкновения». Только жестко связанный с массивным протоном электрон лишен возможности свободного перемещения. Чтобы практически воспользоваться этим обстоятельством, необходимо взаимодействие двух встречных пучков атомарного водорода. Один пучок «правый» (орбитальные электроны вращаются вокруг протона по часовой стрелке в направлении движения атома), а другой «левый» (движение электронов против часовой стрелки). Эта ситуация показана на фигуре 12.4.2.3 для двух соседних атомов с противоположным направлением движения.
|
|
|
|
|
|
На фигуре 12.4.2.4 показана конструкция более совершенного компактного реактора
ядерного синтеза любой желаемой мощности.
На фигуре: 1 – термостойкий герметичный цилиндр, заполненный водородом, 2 – обмотка соленоида для создания внутри цилиндра магнитного поля, 3 – ребра отбора тепла, 4 – теплоноситель, 5 – окно, прозрачное для излучения для запуска реактора, 6 – запускающее излучение.
Размеры реактора могут быть любыми от размера карандаша до любого, определяемого потребностями по мощности.
Работает реактор следующим образом. Цилиндр 1 заполняется водородом и герметично закрывается окном 5. Далее производится диссоциация молекул водорода до атомарного водорода или нагревом тем или иным способом водорода в цилиндре или излучением через окно 5, способным разложить молекулы водорода на отдельные атомы. Атомы водорода ориентируются в магнитном поле так, что орбитальные магнитные моменты электронов будут направлены в одну сторону, как показано на фигуре 12.4.2.3. Таким образом создаются условия для столкновения электронов и образования нейтронов, которые в последующих реакциях создают дейтерий, тритий, гелий и все остальные химические элементы. Понятно, что вероятность столкновения электронов мала и скорость ядерного синтеза целиком определяется скоростью генерирования нейтронов, т.к. реакции с их участием идут без затруднений. На фигуре 12.4.2.4 показан реактор периодического действия типа бака с бензином, который приходится пополнять. В реакторе непрерывного действия после возбуждения генерирования нейтронов через цилиндр медленно прокачивают водород.
Идеальные условия для ядерного синтеза столкновением электронов имеются у космических объектов, содержащих водород и мощное магнитное поле (Юпитер, звезды). Поэтому понятно откуда у Солнца появились тяжелые элементы, например, свинец. В связи с изложенным, возникают большие сомнения в разделении звезд на два поколения. Кроме того, внутри звезд происходят такие ядерные процессы, о которых официальная наука пока не догадывается. Описанный механизм генерирования нейтронов должен реализоваться в обширных облаках атомарного водорода и дать ответ на вопрос: откуда в космосе появляются свободные нейтроны?
Еще один предлагаемый способ получения ядерной энергии можно назвать управляемой протонной трансмутацией ядер (см. главу 29.7.3) или фотоэлектронной эмиссией ядер. В главе 6.1. было показано, что энергия связи электрона с протоном в нейтронах ядер атомов примерно одинакова для любых ядер и составляет 0,76476 Мэв. Следовательно, фотоны с этой энергией способны выбивать электроны из нейтронов ядра. Этот эффект можно назвать фотоэлектронной эмиссией ядер по аналогии с известной фотоэлектронной эмиссией. В результате облучения любого вещества фотонами с такой энергией нейтроны ядер распадаются на электрон и протон. Продукты распада нейтрона не могут удерживаться на поверхности ядра и покидают его. Таким образом, в процессе облучения ядра атомов постепенно превращаются в водород. По-видимому, указанный механизм образования водорода действует вблизи космических источников жесткого электромагнитного излучения. Очевидно, что управляемая протонная трансмутация является энергетически выгодным процессом, т.к. затрачивая 0,8 Мэв на каждый нейтрон мы получаем минимум 8 Мэв энергии не считая той, которая выделится при распаде пересыщенных протонами ядер.
12.4.3. Ударный термоядерный синтез с предварительным сжатием
Посвящаю своему старшему сыну в его день рождения.
Кроме «поджига» (глава 12.4.1) мы в детстве забавлялись и «гранатой», правда, недолго, т.к. эта игрушка смертельно опасна. Два болта скручиваются как можно сильнее в одной гайке. Между ними накрошены 5-6 спичечных головок. Если «гранату» резко бросить на камень, то в результате детонации осколки «гранаты» трудно разыскать.
В применении к теме этой главы «граната» выглядит, как показано на фигуре 12.4.3.1.
На фигуре: 1 – корпус снаряда, 2 – передний болт, 3 – задний болт, 4 – ударник, 5 – проточки под ключ, 6 – заглушка, 7 – таблетка термоядерного горючего в металлической оболочке, 8 – взрывчатое вещество, 9 – втулка с конусной полостью, 10 – смазка, 11 – резьбовая втулка.
|
|
|
|
|
|
Снаряд монтируется в соответствии с фигурой. С помощью проточек 5 болты с мелкой резьбой 2 и 3 стягиваются в резьбовой втулке 11 так, что давление между ними достигает несколько тысяч атмосфер. С заднего конца снаряда плотно навернута (резьба не показана) заглушка 6. Чтобы исключить крутящие моменты при создании предварительного сжатия, между болтом 3 и втулкой 9 помещают каплю смазки 10.
При выстреле снаряда 1 в твердое препятствие, ударник 4 воздействует на болт 2. Ударная волна проходит через термоядерный заряд 7, предварительно его разогревая и вызывает детонацию взрывчатого вещества 8, которое при детонации создает встречную ударную волну и кумулятивную струю в направлении термоядерного заряда. В результате происходит реакция термоядерного синтеза, а массивный корпус 1 снаряда обеспечивает инерционное удержание термоядерных реагентов.
12.5. Энергетические уровни ядер
Поскольку устройства ядер официальная физика не знает, то их свойства описываются излюбленным приемом ортодоксов – подгонкой под ответ: «Подбирая порядок уровней тонкой и грубой структуры удалось объяснить магические числа, спин и магнитный момент большинства ядер» (Н.И. Карякин и др. Краткий справочник по физике. Москва, 1962, стр. 426). В этой главе я попытаюсь дать лишь качественное описание систем энергетических уровней ядер. Это обусловлено достаточной сложностью количественных вычислений, а любые упрощения ничем не отличаются от откровенной подгонки под нужные результаты.
Новая физика различает несколько систем энергетических уровней ядер, которые связывает:
1. С изомерией ядер.
2. С различным расположением поверхностных избыточных нейтронов.
3. С различными уровнями энергии нейтрона.
Рассмотрим каждую систему подробно.
Ядерные изомеры.
Любое ядро имеет большие возможности для образования многочисленных изомеров. Например, ядро урана (579997) (см. главу 12) возможно в вариантах: (379999), (779995), (15799951), (399997), и т.д. Такие изомеры могут иметь отличия в энергетических уровнях порядка средней энергии связи нуклона в ядре (несколько Мэв).
Расположение избыточных нейтронов.
Избыточные нейтроны не могут находиться внутри кристаллической решетки a-частиц,
поэтому располагаются только на поверхности ядра. У разных изотопов одного
элемента разное количество избыточных нейтронов, поэтому энергетические уровни
их также могут отличаться на несколько Мэв. Для
данного изотопа можно ввести понятие «нейтронных изомеров». Количество
избыточных нейтронов никогда не достигает теоретически предельного значения
(глава 12) из-за резкого увеличения интенсивности бета-распада, поэтому
остается много вакантных мест, как на границе a-плоскостей, так и на самих
наружных плоскостях. Поэтому в зависимости от расположения нейтронов возможно
множество нейтронных изомеров ядра с энергетическими уровнями порядка 1 Мэв.
Кроме того, ядра вращаются и ось вращения по энергетическим соображениям должна
быть перпендикулярна ![]() -плоскостям.
Тогда возникает возможность для многочисленных дополнительных нейтронных
изомеров в зависимости от того, располагается ли данный нейтрон ближе к «полюсу»
или к «экватору». Здесь разница в уровнях энергии будет еще меньше.
-плоскостям.
Тогда возникает возможность для многочисленных дополнительных нейтронных
изомеров в зависимости от того, располагается ли данный нейтрон ближе к «полюсу»
или к «экватору». Здесь разница в уровнях энергии будет еще меньше.
Уровни энергии нейтрона.
В основном состоянии электрон, образующий с протоном нейтрон, обладает энергией связи 1,293 Мэв, что соответствует разнице масс нейтрона и протона. В этом состоянии электрон очень напоминает основное состояние в атоме водорода. Поэтому возможны многочисленные уровни энергии отдельного нейтрона вплоть до его «ионизации» - излучения электрона и превращения в протон. В этой системе многочисленных уровней максимально возможная энергия равна 1,293 Мэв.
Таким образом, каждое ядро имеет так много возможных энергетических состояний, что легко подогнать под них любую ложную теорию.