10. В ЗАКЛЮЧЕНИЕ ОБ ЭЛЕМЕНТАРНЫХ ЧАСТИЦАХ
Вполне возможно, и даже наверняка можно утверждать, что в представленной картине "элементарных" частиц есть неточности, особенно это касается электронных нейтрино, которые свое присутствие почти не обнаруживают. Приходилось оперировать всего одним уравнением с тремя неизвестными, но принцип ясен: эти частицы представляют собой некое подобие химических соединений и число таких соединений не ограничено. В изложенные представления укладываются все без исключения объективные свойства частиц.
Новая физика предлагает простую картину элементарных
частиц. Все они в конечном итоге состоят из электронного нейтрино и
антинейтрино. Эти базовые частицы образуют фундаментальные стабильные частицы
(с античастицами): остальные типы нейтрино, электрон, протон и фотон.
Стабильные частицы образуют квазистабильные и нестабильные (резонансы). Время
жизни квазистабильных частиц составляет от 900 сек для свободного нейтрона до
10-20 сек для ![]() -гиперона. Компоненты этих частиц находятся в
первом квантовом состоянии (не обладают кратным моментом импульса), поэтому они
относительно устойчивы. Чем меньше число компонентов, тем более устойчива
квазистабильная частица. Наличие компонентов способных к аннигиляции (например,
электрона и позитрона) резко сокращает время жизни квазистабильной частицы.
Резонансы имеют время жизни, порядка 10-23 сек. Это
обусловлено тем, что компоненты нестабильных частиц имеют кратный момент
импульса, т.е. находятся в возбужденном состоянии. За время 10-23 сек
компоненты переходят в основное состояние и резонанс распадается на
квазистабильные и, в конце концов, стабильные частицы. На этом основании
резонансы могут считаться отдельными частицами лишь условно. Состояние
какого-либо компонента нестабильной частицы одновременно похоже на состояние
возбужденного электрона в атоме и на квантовое состояние планет Солнечной
системы (см. соответствующую главу). Это вновь демонстрирует удивительную
общность законов на всех уровнях мироздания. Момент импульса компонента
элементарной частицы равен mCr. Чтобы увеличить момент импульса в два раза, необходимо
увеличить в два раза массу компонента, т.к. движение со скоростью света
изменить невозможно. Также невозможно увеличить вдвое радиус орбиты, т.к. при
этом гравидинамическое взаимодействие практически исчезнет. Таким образом, если
квантовое состояние электрона в данном резонансе равно 5, то это означает, что
по орбите движется электрон с массой в 5 раз больше той, которая была бы в
основном квантовом состоянии (обозначим такой электрон (5)e-). Время жизни резонанса уменьшается с увеличением числа
его компонентов и от квантового состояния каждого компонента слабо зависит.
Приведем несколько примеров строения резонансов. Резонанс f2 имеет массу 1274 Мэв и строение (9)e+(9)e-. Поскольку
электрон в основном состоянии на орбите имеет момент импульса
-гиперона. Компоненты этих частиц находятся в
первом квантовом состоянии (не обладают кратным моментом импульса), поэтому они
относительно устойчивы. Чем меньше число компонентов, тем более устойчива
квазистабильная частица. Наличие компонентов способных к аннигиляции (например,
электрона и позитрона) резко сокращает время жизни квазистабильной частицы.
Резонансы имеют время жизни, порядка 10-23 сек. Это
обусловлено тем, что компоненты нестабильных частиц имеют кратный момент
импульса, т.е. находятся в возбужденном состоянии. За время 10-23 сек
компоненты переходят в основное состояние и резонанс распадается на
квазистабильные и, в конце концов, стабильные частицы. На этом основании
резонансы могут считаться отдельными частицами лишь условно. Состояние
какого-либо компонента нестабильной частицы одновременно похоже на состояние
возбужденного электрона в атоме и на квантовое состояние планет Солнечной
системы (см. соответствующую главу). Это вновь демонстрирует удивительную
общность законов на всех уровнях мироздания. Момент импульса компонента
элементарной частицы равен mCr. Чтобы увеличить момент импульса в два раза, необходимо
увеличить в два раза массу компонента, т.к. движение со скоростью света
изменить невозможно. Также невозможно увеличить вдвое радиус орбиты, т.к. при
этом гравидинамическое взаимодействие практически исчезнет. Таким образом, если
квантовое состояние электрона в данном резонансе равно 5, то это означает, что
по орбите движется электрон с массой в 5 раз больше той, которая была бы в
основном квантовом состоянии (обозначим такой электрон (5)e-). Время жизни резонанса уменьшается с увеличением числа
его компонентов и от квантового состояния каждого компонента слабо зависит.
Приведем несколько примеров строения резонансов. Резонанс f2 имеет массу 1274 Мэв и строение (9)e+(9)e-. Поскольку
электрон в основном состоянии на орбите имеет момент импульса ![]() , то ГКЧ этого резонанса
будет равно 18, а масса: 18×70,03=1260 Мэв. Недостающие 14 Мэв связаны с тем, что при
данном расчете мы не учитываем усиления гравидинамического взаимодействия
компонентов за счет их кратных масс, в результате чего радиус орбит немного
уменьшается, а масса увеличивается для сохранения момента импульса. Резонансы
, то ГКЧ этого резонанса
будет равно 18, а масса: 18×70,03=1260 Мэв. Недостающие 14 Мэв связаны с тем, что при
данном расчете мы не учитываем усиления гравидинамического взаимодействия
компонентов за счет их кратных масс, в результате чего радиус орбит немного
уменьшается, а масса увеличивается для сохранения момента импульса. Резонансы ![]() : (6)e+(5)
: (6)e+(5)![]() (5)
(5)![]() (?)
(?)![]() ,
, ![]() : (6)e-(5)
: (6)e-(5) ![]() (5)
(5) ![]() (?)
(?)![]() и
и ![]() : (4)e+(4)e-(3)
: (4)e+(4)e-(3) ![]() (3)
(3)
![]() имеют ГКЧ
равное 11 и массу: 11×70,03=770 Мэв. Опытное значение их масс равно 768 Мэв.
Поскольку верхнего порога для энергии частицы не существует, то мы всегда будем
открывать резонансы с любыми массами, и число их не ограничено. Здесь следует
сделать одно замечание в адрес ортодоксальных представлений о времени жизни
элементарных частиц. Считается, что распад квазистабильных частиц обусловлен
так называемым электромагнитным и слабым взаимодействием, а распад резонансов –
сильным взаимодействием. Логика подсказывает, что все должно быть наоборот –
чем сильнее гравидинамическое взаимодействие, тем стабильнее частица.
имеют ГКЧ
равное 11 и массу: 11×70,03=770 Мэв. Опытное значение их масс равно 768 Мэв.
Поскольку верхнего порога для энергии частицы не существует, то мы всегда будем
открывать резонансы с любыми массами, и число их не ограничено. Здесь следует
сделать одно замечание в адрес ортодоксальных представлений о времени жизни
элементарных частиц. Считается, что распад квазистабильных частиц обусловлен
так называемым электромагнитным и слабым взаимодействием, а распад резонансов –
сильным взаимодействием. Логика подсказывает, что все должно быть наоборот –
чем сильнее гравидинамическое взаимодействие, тем стабильнее частица.
Из представленных схем строения элементарных частиц видно,
что официальная классификация частиц имеет в представлении новой физики
определенный физический смысл. Лептоны состоят из электронов и нейтрино, им
приписывают квантовое число – лептонный заряд. В мезонах появляются совместно
существующие частица и античастица лептонов, а в составе странных мезонов
появляются пионы. В барионах обязательно присутствие протона (или антипротона),
поэтому барионам приписывают квантовое число – барионный заряд. Очевидно, что
лептонный и барионный заряд сохраняются при превращениях частиц, т.к. описывают
фундаментальные стабильные частицы, которые могут появляться или исчезать
только в паре со своей античастицей. Так называемые зарядовые мультиплеты
(протон-нейтрон, пионы и т.п.) относятся к частицам с одинаковым значением ГКЧ,
хотя они могут иметь разное строение. У странных барионов квантовое число
странность соответствует количеству пионов в составе частицы, например у ![]() -гиперона один пион (фиг.
9.6.2.1) странность –1, у
-гиперона один пион (фиг.
9.6.2.1) странность –1, у ![]() -гиперонов странность тоже –1 и тоже в
составе один пион (фиг. 9.6.3.1), у
-гиперонов странность тоже –1 и тоже в
составе один пион (фиг. 9.6.3.1), у ![]() -гиперонов странность –2 и в составе
частиц по 2 пиона (фиг. 9.6.4.1), у
-гиперонов странность –2 и в составе
частиц по 2 пиона (фиг. 9.6.4.1), у ![]() -гиперона странность –3 и в составе этой
частицы 3 пиона (фиг. 9.6.5.1). Таким образом, обычные частицы входят в состав странных,
странные входят в состав очарованных, а очарованные в состав прелестных.
Официальная физика не знает причин происхождения квантовых чисел элементарных
частиц. Современная кварковая модель мезонов и барионов не объясняет
происхождение квантовых чисел. Она не дает также значений масс частиц, хотя при
определенном кварковом составе масса частиц должна была бы легко определяться.
-гиперона странность –3 и в составе этой
частицы 3 пиона (фиг. 9.6.5.1). Таким образом, обычные частицы входят в состав странных,
странные входят в состав очарованных, а очарованные в состав прелестных.
Официальная физика не знает причин происхождения квантовых чисел элементарных
частиц. Современная кварковая модель мезонов и барионов не объясняет
происхождение квантовых чисел. Она не дает также значений масс частиц, хотя при
определенном кварковом составе масса частиц должна была бы легко определяться.
10.1. Спектр масс элементарных частиц.
Определение массы элементарной частицы (в Мэв) по формуле:
m=70,03∙N (10.1.1),
где N –главное квантовое число (целые числа от 1 до ![]() ) является лишь первым
приближением из формулы (5.4.4) при двух предположениях: 1. Радиус орбиты
составляющих частицы равен радиусу электрона (2,81785 фм). 2. Суммарный момент
импульса (ГКЧ) имеет целое значение. В реальных частицах эти предположения не
точны, например, радиус мюонов меньше радиуса электрона и составляет 2,8014 фм,
поэтому расчетная масса по (10.1.1) оказывается меньше экспериментальной на 0,6
Мэв за счет уменьшения радиуса орбиты. Радиус орбиты уменьшается из-за
гравидинамического притяжения материи e- -
) является лишь первым
приближением из формулы (5.4.4) при двух предположениях: 1. Радиус орбиты
составляющих частицы равен радиусу электрона (2,81785 фм). 2. Суммарный момент
импульса (ГКЧ) имеет целое значение. В реальных частицах эти предположения не
точны, например, радиус мюонов меньше радиуса электрона и составляет 2,8014 фм,
поэтому расчетная масса по (10.1.1) оказывается меньше экспериментальной на 0,6
Мэв за счет уменьшения радиуса орбиты. Радиус орбиты уменьшается из-за
гравидинамического притяжения материи e- - ![]() или антиматерии e+
-
или антиматерии e+
- ![]() . Материя и
антиматерия слабо взаимодействуют внутри элементарных частиц, поэтому радиус орбиты
может увеличиться и расчетное значение массы частицы станет больше
экспериментального. Например, в
. Материя и
антиматерия слабо взаимодействуют внутри элементарных частиц, поэтому радиус орбиты
может увеличиться и расчетное значение массы частицы станет больше
экспериментального. Например, в ![]() радиус орбиты составляет 2,924 фм за счет
слабого гравидинамического притяжения электрона и позитрона, и расчетное
значение массы превышает экспериментальное на 5,1 Мэв. У заряженных пионов
радиус орбиты 2,8277 фм за счет ослабления связи e- -
радиус орбиты составляет 2,924 фм за счет
слабого гравидинамического притяжения электрона и позитрона, и расчетное
значение массы превышает экспериментальное на 5,1 Мэв. У заряженных пионов
радиус орбиты 2,8277 фм за счет ослабления связи e- - ![]() или e+
-
или e+
- ![]() поэтому их
расчетная масса на 0,5 Мэв больше экспериментальной, а заряженные пионы тяжелее
нейтрального на 4,6 Мэв. Поскольку нейтральные каоны содержат заряженный пион,
а заряженные каоны вместо заряженного имеют нейтральный пион, то их массы
больше на 4 Мэв, а не на 4,6 Мэв за счет слабой связи e- -
поэтому их
расчетная масса на 0,5 Мэв больше экспериментальной, а заряженные пионы тяжелее
нейтрального на 4,6 Мэв. Поскольку нейтральные каоны содержат заряженный пион,
а заряженные каоны вместо заряженного имеют нейтральный пион, то их массы
больше на 4 Мэв, а не на 4,6 Мэв за счет слабой связи e- - ![]() или e+
-
или e+
- ![]() (фиг. 9.5.1).
Уточненное ГКЧ частиц не имеет целого значения из-за наличия составляющих на
орбите со значением момента импульса не равного
(фиг. 9.5.1).
Уточненное ГКЧ частиц не имеет целого значения из-за наличия составляющих на
орбите со значением момента импульса не равного ![]() , например
, например ![]() /2 или
/2 или ![]() /137,0391. Если в ГКЧ мюонов учтем
электронное нейтрино или антинейтрино с моментом импульса 0,0036
/137,0391. Если в ГКЧ мюонов учтем
электронное нейтрино или антинейтрино с моментом импульса 0,0036![]() , то разница между
расчетным и экспериментальным значением масс мюонов составит уже не 0,6 Мэв, а
0,36 Мэв, т.е. отклонение не превышает 0,35% даже без учета взаимодействия
между электроном (позитроном) и мюонным антинейтрино (мюонным нейтрино). Кроме
всего прочего для многих частиц необходимо учитывать и электростатическое
взаимодействие составляющих. Это хорошо видно на примере фигуры (9.6.3.1):
, то разница между
расчетным и экспериментальным значением масс мюонов составит уже не 0,6 Мэв, а
0,36 Мэв, т.е. отклонение не превышает 0,35% даже без учета взаимодействия
между электроном (позитроном) и мюонным антинейтрино (мюонным нейтрино). Кроме
всего прочего для многих частиц необходимо учитывать и электростатическое
взаимодействие составляющих. Это хорошо видно на примере фигуры (9.6.3.1): ![]() (1189 Мэв),
(1189 Мэв), ![]() (1193 Мэв) и
(1193 Мэв) и ![]() (1197 Мэв). Массы этих
гиперонов увеличиваются параллельно с увеличением электростатического
притяжения мюонов к протону. Таким образом, учет эффектов второго порядка
позволяет найти более точную массу любой элементарной частицы. В связи с изложенным,
можно предложить таблицу масс элементарных частиц которые они приобретают,
двигаясь по орбите в составе более сложной частицы.
(1197 Мэв). Массы этих
гиперонов увеличиваются параллельно с увеличением электростатического
притяжения мюонов к протону. Таким образом, учет эффектов второго порядка
позволяет найти более точную массу любой элементарной частицы. В связи с изложенным,
можно предложить таблицу масс элементарных частиц которые они приобретают,
двигаясь по орбите в составе более сложной частицы.
Таблица 10.1.1
|
Частица |
Масса на орбите, Мэв |
Примечание |
|
Электронное нейтрино |
0,255 для ГКЧ |
- |
|
Электрон (позитрон) |
70,03 для ГКЧ |
- |
|
Мюонное нейтрино |
35,015 для ГКЧ |
- |
|
Пион |
210,09 для ГКЧ 205,00 для 209,60 для |
Входит в «странные» частицы |
|
Каон |
560,24 для ГКЧ 567,70 для K0 563,68 для |
Входит в «очарованные» частицы |
|
Очарованный мезон D |
1925,8 для ГКЧ 1930,9 для D0 1935,5 для |
Входит в «прелестные» частицы |
Пользуясь этой таблицей можно уточнить строение «стабильных» элементарных частиц.
Пока отсутствуют сведения, что барионы как целое могут двигаться по орбите в составе других частиц при этом в продуктах распада будут два протона, поэтому состав элементарных частиц не отличается большим разнообразием составляющих. Общая масса элементарной частицы приблизительно равна сумме масс составляющих из средней колонки таблицы (без учета разницы гравидинамического взаимодействия материя-материя (антиматерия-антиматерия) и материя-антиматерия и электростатического взаимодействия). Кроме того, в составе любой частицы наблюдается не много отдельных составляющих (которые сами могут состоять из нескольких).
Современная физика в вопросе теории элементарных частиц так усложнила проблему, что ее «достижения» воспринимаются человеком, имеющим хоть немного здравого смысла, как сплошной бред. Каждая частица буквально кричит исследователю о своей структуре – смотрите по реакциям распада, что было у меня внутри. Но ортодокс упрямо отрицает очевидные факты. Иначе нужно пересматривать основы современной физики (фактически превратившуюся в религию). В связи с этим есть необходимость добавить к уже описанным дополнительные частицы, воспользовавшись данными из Субатомная физика, Издательство Московского университета, 1994 г. Эту добавку автор делает для демонстрации научной молодежи альтернативного пути. Вместо картинок будем приводить состав элементарных частиц (вид компонентов этих частиц изображен ранее).
Легкий мезон ![]() . Его масса 548,8 Мэв, ГКЧ=8,
расчетная масса по ГКЧ 560,2 Мэв, а по таблице 10.1.1 550,06 Мэв. Состав
. Его масса 548,8 Мэв, ГКЧ=8,
расчетная масса по ГКЧ 560,2 Мэв, а по таблице 10.1.1 550,06 Мэв. Состав ![]()
![]() e+e-.
Очень короткое время жизни обусловлено наличием нейтральных пионов в составе
мезона и наличие электрона и позитрона совместно.
e+e-.
Очень короткое время жизни обусловлено наличием нейтральных пионов в составе
мезона и наличие электрона и позитрона совместно.
Очарованные мезоны.
![]() .
Масса 1869,3 Мэв, ГКЧ=26,5, расчетная масса по ГКЧ 1855,8 Мэв. Состав
.
Масса 1869,3 Мэв, ГКЧ=26,5, расчетная масса по ГКЧ 1855,8 Мэв. Состав ![]()
![]() e+
e+![]() К0
К0 ![]()
![]()
![]() ,
, ![]()
![]() e-К+К0
e-К+К0 ![]()
![]()
![]() ,
(1865,5 Мэв по таблице 10.1.1)
,
(1865,5 Мэв по таблице 10.1.1)
D0. Масса 1864,5 Мэв, ГКЧ=26,5 расчетная масса
по ГКЧ 1855,8 Мэв. Состав ![]()
![]() e+
e+![]() К0
К0 ![]()
![]()
![]() ,
, ![]()
![]() e-К+К0
e-К+К0 ![]()
![]()
![]() , (1860,9 Мэв по таблице 10.1.1). Заряженный
пион тяжелее нейтрального, поэтому
, (1860,9 Мэв по таблице 10.1.1). Заряженный
пион тяжелее нейтрального, поэтому ![]() тяжелее D0 на 4,6 Мэв (см. о
пионах в начале главы).
тяжелее D0 на 4,6 Мэв (см. о
пионах в начале главы).
![]() .
Масса 1968,8 Мэв, ГКЧ=28, расчетная масса по ГКЧ 1960,8 Мэв. Состав К+
.
Масса 1968,8 Мэв, ГКЧ=28, расчетная масса по ГКЧ 1960,8 Мэв. Состав К+![]() К0
К0 ![]()
![]()
![]() (масса
по таблице 10.1.1 1970,3 Мэв).
(масса
по таблице 10.1.1 1970,3 Мэв).
![]() .
Масса 2110,3 Мэв, ГКЧ=30, расчетная масса по ГКЧ 2100,9 Мэв. Состав
.
Масса 2110,3 Мэв, ГКЧ=30, расчетная масса по ГКЧ 2100,9 Мэв. Состав ![]() К0К0
К0К0 ![]()
![]() (масса по таблице 10.1.1
2109,1 Мэв).
(масса по таблице 10.1.1
2109,1 Мэв).
B-мезоны (прелестные).
![]() Масса
5277,6 Мэв, ГКЧ=75, расчетная масса по ГКЧ 5252,3 Мэв. Состав K+
Масса
5277,6 Мэв, ГКЧ=75, расчетная масса по ГКЧ 5252,3 Мэв. Состав K+![]() D+
D+![]()
![]()
![]()
![]() (масса по таблице 10.1.1 5273,6 Мэв).
(масса по таблице 10.1.1 5273,6 Мэв).
B0. Масса 5279,4 Мэв, ГКЧ=75, расчетная масса по
ГКЧ 5252,3 Мэв. Состав K+![]() D+
D+![]()
![]() e-
e-![]() , K+
, K+![]() D+
D+![]()
![]() e+
e+![]() (масса по таблице 10.1.1 5278,2 Мэв).
(масса по таблице 10.1.1 5278,2 Мэв).
Очарованные барионы. Здесь нужно сделать следующее замечание. Поскольку в центре барионов находится протон и поэтому барионы представляют некое подобие водородоподобных атомов, то формальное ГКЧ протона 938,27:70,03=13,4. Поэтому формальный подсчет массы по ГКЧ дает завышенное значение массы на 0,4∙70,03=28 Мэв. Массу протона примем равной 938,27 Мэв.
![]() .
Масса 2285,2 Мэв, ГКЧ=32. Состав P+K+
.
Масса 2285,2 Мэв, ГКЧ=32. Состав P+K+![]()
![]() (масса по таблице 10.1.1
2278,7 Мэв).
(масса по таблице 10.1.1
2278,7 Мэв).
![]() .
Масса 2453,0 Мэв, ГКЧ=35, расчетная масса по таблице 10.1.1 2488,3 Мэв. Состав P+K+
.
Масса 2453,0 Мэв, ГКЧ=35, расчетная масса по таблице 10.1.1 2488,3 Мэв. Состав P+K+
![]()
![]()
![]() .
.
![]() .
Масса 2453,2 Мэв, ГКЧ=35, расчетная масса по таблице 10.1.1 2483,7 Мэв. Состав P+K+
.
Масса 2453,2 Мэв, ГКЧ=35, расчетная масса по таблице 10.1.1 2483,7 Мэв. Состав P+K+![]()
![]()
![]() .
.
![]() .
Масса 2452,7 Мэв, ГКЧ=35, расчетная масса по таблице 10.1.1 2488,3 Мэв. Состав P+K+
.
Масса 2452,7 Мэв, ГКЧ=35, расчетная масса по таблице 10.1.1 2488,3 Мэв. Состав P+K+![]()
![]()
![]() .
.
Все эти барионы содержат в своем составе пион и компоненты ![]() , поэтому в продуктах
распада наблюдаются 100% именно этих частиц. Вместе с сильно завышенной
расчетной массой этот факт, возможно, указывает на строение
, поэтому в продуктах
распада наблюдаются 100% именно этих частиц. Вместе с сильно завышенной
расчетной массой этот факт, возможно, указывает на строение ![]() -барионов в виде центрального ядра
вокруг которого вращается пион во втором орбитальном слое. В этом случае
орбитальный момент пиона будет не
-барионов в виде центрального ядра
вокруг которого вращается пион во втором орбитальном слое. В этом случае
орбитальный момент пиона будет не ![]() , а
, а ![]() /2 и расчетное значение массы будет
соответствовать опытному значению.
/2 и расчетное значение массы будет
соответствовать опытному значению.
![]() .
Масса 2466,8 Мэв, ГКЧ=35, расчетная масса по таблице 10.1.1 2483,7 Мэв. Состав P+K0K0
.
Масса 2466,8 Мэв, ГКЧ=35, расчетная масса по таблице 10.1.1 2483,7 Мэв. Состав P+K0K0
![]()
![]() .
.
![]() .
Масса 2473,0 Мэв, ГКЧ=35, расчетная масса по таблице 10.1.1 2488,3 Мэв. Состав P+K0K0
.
Масса 2473,0 Мэв, ГКЧ=35, расчетная масса по таблице 10.1.1 2488,3 Мэв. Состав P+K0K0 ![]()
![]() .
.
Относительно резонансов напомню, что аналогично тому, как электрон в атоме переходит из одного возбужденного уровня на другой и ему на это требуется примерно 10-8 секунды, возбужденные компоненты резонанса разрушают резонанс за один оборот по орбите и им требуется на это 10-23 секунды, поэтому резонансы не могут считаться полноценными частицами.
Таким образом, спектр масс элементарных частиц подтверждает незыблемость закона сохранения момента количества движения в микромире, следствием которого является возникновение массы.
Точное выражение для расчета массы частицы основано на формулировке закона сохранения момента количества движения (S) с учетом того, что компоненты элементарной частицы двигаются со световой скоростью:
m=S/Сr (10.1.2).
Чтобы получить значение массы в энергетических единицах (Мэв), нужно (10.1.2) умножить на С2:
m=SС/r (10.1.3).
Масса электрона по ГКЧ (S=![]() /137,036): 70,03/137,036=0,51103
Мэв
/137,036): 70,03/137,036=0,51103
Мэв
Данные по «Субатомная физика». Издательство Московского университета, 1994:
![]() =
6,582122∙10-22 Мэв∙с
=
6,582122∙10-22 Мэв∙с
![]() = 1/137,0359895=0,00729735308
= 1/137,0359895=0,00729735308
C = 2,997924∙108 м∙с-1
re = 2,81794092∙10-15 м
Табличное значение me = 0,5109991 Мэв
Масса электрона по (10.1.3): 0,510998968 Мэв
Радиус нейтрона (мои данные по магнитному моменту) rn=0,986∙10-15 м
Масса электрона на орбите 0,986∙10-15 м по (10.1.3): 1,46041 Мэв. По экспериментальным данным нейтрон тяжелее протона на 1,29332 Мэв. Радиус нейтрона был рассчитан по магнитному моменту нейтрона в предположении точечности нейтрино, образующих электрон. Фактически нейтрино имеют конечные размеры, поэтому движущемуся по окружности заряженному шарику необходим немного больший радиус для создания такого же магнитного поля, как заряженной точке. Поэтому реальный радиус электрона, внутри которого находится протон, больше рассчитанного, что приводит к завышенному на 0,16709 Мэв значению массы электрона. Таким образом, на примере расчета масс нейтрона и электрона не только подтверждена методика расчета спектра масс частиц, но и строение нейтрона и ошибка официальной физики в отношении собственного момента импульса электрона.
Здесь следует сказать несколько слов об увеличении времени жизни быстро распадающихся частиц с увеличением их скорости движения. Обычно это объясняется тем, что для них течение времени изменяется. Далее мы увидим, что время абсолютно (вернее, является вместилищем событий, не обладая никакими физическими свойствами, поскольку не является физическим объектом). С возрастанием скорости, радиус винтовой линии движения свободных частиц уменьшается, что указывает на увеличение гравидинамического поля и упрочнение связей отдельных составляющих частицы. Некоторые частицы таким способом можно сделать стабильными, если они постоянно будут двигаться с большой скоростью или будут "неподвижными", но в мощном внешнем гравидинамическом поле, т.е. глубокой потенциальной яме (нейтроны в ядре). Очевидно, что изменение хода времени не может нестабильную частицу сделать стабильной, а может лишь оттянуть время распада.
Упрочнение связей в гравидинамических системах наглядно
видно из строения частиц, которые содержат пион ![]() время жизни которого в свободном
состоянии составляет 8,4×10-17 сек (т.к. электрон и позитрон из-за
электростатического притяжения дестабилизируют друг друга на орбите), а в
составе этих частиц (при движении пиона
время жизни которого в свободном
состоянии составляет 8,4×10-17 сек (т.к. электрон и позитрон из-за
электростатического притяжения дестабилизируют друг друга на орбите), а в
составе этих частиц (при движении пиона ![]() почти со световой скоростью) оно уже не
менее 2,9×10-10 сек (
почти со световой скоростью) оно уже не
менее 2,9×10-10 сек (![]() -барион). Таким образом, использование
гравидинамического поля является мощным рычагом управления процессами распада
частиц любого рода. Разгоняя ионы радиоактивных атомов или нейтральные частицы,
удастся в некоторых случаях полностью предотвратить распад. Как это лучше
сделать, будет ясно из дальнейшего. Во всяком случае, можно уверенно
предполагать существование в космосе далеких трансурановых элементов, особенно
на окраинах Вселенной, где объекты двигаются с околосветовыми скоростями.
Типичные гравидинамические объекты можно наблюдать и в ближнем космосе,
например, короткопериодические двойные звезды, пульсары.
-барион). Таким образом, использование
гравидинамического поля является мощным рычагом управления процессами распада
частиц любого рода. Разгоняя ионы радиоактивных атомов или нейтральные частицы,
удастся в некоторых случаях полностью предотвратить распад. Как это лучше
сделать, будет ясно из дальнейшего. Во всяком случае, можно уверенно
предполагать существование в космосе далеких трансурановых элементов, особенно
на окраинах Вселенной, где объекты двигаются с околосветовыми скоростями.
Типичные гравидинамические объекты можно наблюдать и в ближнем космосе,
например, короткопериодические двойные звезды, пульсары.
Сравнивая строение нейтрона (фиг.9.6.1.1) со строением
одного из вариантов ![]() пиона
(фиг.9.3.2), мы можем утверждать, что соединение
пиона
(фиг.9.3.2), мы можем утверждать, что соединение ![]() с протоном даст некое подобие нейтрона
или нейтрон в чистом виде, а сам нейтрон представляет собой разновидность
с протоном даст некое подобие нейтрона
или нейтрон в чистом виде, а сам нейтрон представляет собой разновидность ![]() гиперона (фиг.9.6.2.1)
или
гиперона (фиг.9.6.2.1)
или ![]() гиперона.
Таким образом, со временем, мы сможем изучать ядра атомов, содержащие вместо
нейтронов
гиперона.
Таким образом, со временем, мы сможем изучать ядра атомов, содержащие вместо
нейтронов ![]() или
или
![]() гипероны.
Для большей ясности этого вопроса, необходимо учитывать, что при соединении
нуклонов в ядре выделяется в среднем 7 Мэв энергии на один нуклон. Этого вполне
достаточно не только для образования пар нейтрино-антинейтрино (см. фотон в
главе о фундаментальных частицах), но и пар электрон-позитрон (
гипероны.
Для большей ясности этого вопроса, необходимо учитывать, что при соединении
нуклонов в ядре выделяется в среднем 7 Мэв энергии на один нуклон. Этого вполне
достаточно не только для образования пар нейтрино-антинейтрино (см. фотон в
главе о фундаментальных частицах), но и пар электрон-позитрон (![]() мезонов). Поскольку
мезонов). Поскольку ![]() и
и ![]() мезоны могут
существовать в вариантах
мезоны могут
существовать в вариантах ![]() (e+,
(e+,![]() ) и
) и
![]() (e-,
(e-,![]() ),
то в ядре возможно образование любых известных гиперонов.
Мало того, одновременное испускание некоторыми ядрами
),
то в ядре возможно образование любых известных гиперонов.
Мало того, одновременное испускание некоторыми ядрами ![]() и
и ![]() излучения говорит о
реальности существования
излучения говорит о
реальности существования ![]() -мезонов в ядре. “Барионы со странностью,
отличной от нуля, называются гиперонами. Легчайшие гипероны (
-мезонов в ядре. “Барионы со странностью,
отличной от нуля, называются гиперонами. Легчайшие гипероны (![]() ,
, ![]() ,
, ![]() ,
, ![]() ) являются долгоживущими частицами и могут
входить в состав атомных ядер, образуя так называемые гиперядра”. “Субатомная
физика”, Издательство Московского университета, 1994, стр.82. Таким образом,
можно говорить не только об электронно-протонном строении ядра, но и об его
позитронно-нейтронном строении. Это обеспечивает сравнительно легкое
взаимопревращение протонов и нейтронов в ядре и образование наиболее устойчивых
вариантов ядер с минимальной потенциальной энергией ядра (см. теорию ядра).
) являются долгоживущими частицами и могут
входить в состав атомных ядер, образуя так называемые гиперядра”. “Субатомная
физика”, Издательство Московского университета, 1994, стр.82. Таким образом,
можно говорить не только об электронно-протонном строении ядра, но и об его
позитронно-нейтронном строении. Это обеспечивает сравнительно легкое
взаимопревращение протонов и нейтронов в ядре и образование наиболее устойчивых
вариантов ядер с минимальной потенциальной энергией ядра (см. теорию ядра).
Когда говорят, что существование позитрона вытекает из уравнения Дирака – это неверно, т.к. представление о позитроне является результатом формального извлечения корня из релятивистского соотношения между энергией и импульсом свободной частицы:
![]() (10.1.4),
(10.1.4),
откуда ![]() (Физика микромира,
«Советская энциклопедия», М., 1980, стр 45-46). Спекуляции вокруг частиц и
античастиц связаны именно с формальным существованием двух значений корня с
противоположными знаками. В классической физике отрицательное значение энергии
свободной частицы не имеет смысла, поэтому его не принимают во внимание, а в
микромире ортодоксальная физика рассматривает и отрицательное значение энергии
на том, якобы, основании, что энергия в микромире меняется порциями. Очевидно,
что два значения энергии с противоположными знаками не зависят от того,
прерывно или непрерывно меняется подкоренное выражение, тем более, что
кинетическая энергия свободной микрочастицы может меняться непрерывно. Новая
физика дает очень простое объяснение существованию античастиц для частиц любого
вида: все частицы состоят из нейтрино и антинейтрино, поэтому симметричная
перемена местами нейтрино и антинейтрино в структуре частицы дает античастицу.
(Физика микромира,
«Советская энциклопедия», М., 1980, стр 45-46). Спекуляции вокруг частиц и
античастиц связаны именно с формальным существованием двух значений корня с
противоположными знаками. В классической физике отрицательное значение энергии
свободной частицы не имеет смысла, поэтому его не принимают во внимание, а в
микромире ортодоксальная физика рассматривает и отрицательное значение энергии
на том, якобы, основании, что энергия в микромире меняется порциями. Очевидно,
что два значения энергии с противоположными знаками не зависят от того,
прерывно или непрерывно меняется подкоренное выражение, тем более, что
кинетическая энергия свободной микрочастицы может меняться непрерывно. Новая
физика дает очень простое объяснение существованию античастиц для частиц любого
вида: все частицы состоят из нейтрино и антинейтрино, поэтому симметричная
перемена местами нейтрино и антинейтрино в структуре частицы дает античастицу.
Чтобы понять, какой физический смысл замаскирован в формуле (10.1.4), вставим в нее выражение для импульса:
![]() (10.1.5),
(10.1.5),
где V – скорость частицы, m – релятивистская масса, которая определяется выражением:
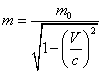 (10.1.6).
(10.1.6).
Именно так получают (10.1.4).
Далее нам потребуется (10.1.6), возведенное во вторую степень:
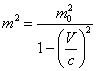 (10.1.7).
(10.1.7).
Подставляя (10.1.6) в (10.1.5) и полученное выражение в (10.1.4), после некоторого преобразования получим:
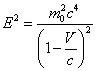 (10.1.8).
(10.1.8).
Подставив (10.1.7)в (10.1.8), найдем:
![]() (10.1.9).
(10.1.9).
Формально извлекая корень из (10.1.9), получим:
![]() (10.1.10).
(10.1.10).
По здравому смыслу отрицательное значение энергии в (10.1.10) надо отбросить, но давайте пойдем по пути извращенцев физического смысла и посмотрим, что из этого получится. Очевидно, что квадрат скорости света не может быть отрицательной величиной, следовательно, после извлечения корня релятивистская масса становится отрицательной. Это возможно только в том случае, если в (10.1.7) скорость движения частицы всегда больше скорости света (такие уроды названы «тахионами»). Тогда квадрат релятивистской массы частицы становится отрицательным, а сама масса – мнимой. Таким образом «тахионы» дважды не имеют никакого смысла.
В заключение необходимо подчеркнуть, что здесь взгляды современной физики приведены очень схематично и намечены только некоторыми штрихами. Совершенно не затронута кварковая модель элементарных частиц, которая усложняется прямо на глазах, косвенно указывая на ложность исходных гипотез. Чтобы избежать трудностей со статистикой, пришлось кваркам приписывать “цвет”. В дальнейшем семейство кварков оказалось необходимым расширить, вводить “очарованные” кварки и т.п. “Термин “очарование”, как и другие квантовые величины, введен совершенно произвольно; об этой величине можно сказать лишь то, что она “действует как очарование”, позволяя устранять трудности теории”. (Подчеркивание мое, чтобы лишний раз обратить внимание читателя на методологию современной физики - В.К.). В этой книге рассматривать все “достижения” ортодоксальной физики не имеет смысла, чтобы уберечь голову читателя. “Причина, вызывающая “размножение” видов кварков, совершенно неясна. Возможно ли, чтобы кварки сами обладали некоторой внутренней структурой? Во всяком случае, их свойства никоим образом не указывают на это. Рост числа видов кварков представляет собой одну из величайших загадок, стоящих сегодня перед физиками”. (В этом утверждении уже содержится отгадка - ложность гипотезы существования кварков в том виде, как она сформулирована - В.К.).
В целом, проблема элементарных частиц в современной физике выглядит следующим образом. “Эта проблема является одной из важнейших современной физики. Необходимо создание новой теории, которая объяснила бы наблюдаемый спектр масс частиц, взаимодействие между ними, времена жизни и другие их характеристики. Первые теории (Гейзенберг) повлекли за собой введение новых физических идей - нелинейное уравнение, квантование пространства. Возможно, что для ее создания потребуется коренная ломка современных представлений” (Н.И. Карякин и др., Краткий справочник по физике, “Высшая школа”, М., 1962, стр. 498). В современной физике элементарных частиц остро стоит проблема, так называемых, расходимостей - бесконечно больших значений физических величин. Например, у точечного электрона получается бесконечно большое значение для энергии кулоновского поля. Чтобы избежать расходимостей, придуман поистине шулерский прием - квантование пространства-времени. Смысл его в том, что вводится понятие минимальной длины l и, соответственно, минимального промежутка времени l/c. Это делается не по требованиям здравого смысла или каких-либо экспериментальных данных, а для того чтобы “устранить” расходимости. Таким образом, пространство и время оказываются “оквантованными”.
Посмотрим, как с точки зрения новой физики выглядит
эффективное сечение рассеяния точечной частицы на твердом шарике радиуса R,
с которым частица не взаимодействует. Очевидно, что для частицы с большой
энергией (малым радиусом r винтовой траектории): ![]() =
=![]() (R+r)2.
Подставляя в эту формулу значение r=
(R+r)2.
Подставляя в эту формулу значение r=![]() /2
/2![]() ,
где
,
где ![]() -
длина волны де Бройля частицы, после некоторых преобразований найдем:
-
длина волны де Бройля частицы, после некоторых преобразований найдем:
![]() (10.2.1).
(10.2.1).
Эта формула будет практически точна до значений ![]()
![]() 2
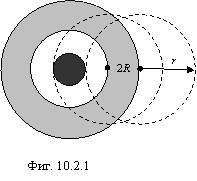
2![]() R. При дальнейшем
увеличении длины волны частицы в мишень попадают только частицы из
"дифракционного" кольца вокруг мишени, как показано на рисунке
10.2.1. Очевидно, что площадь "дифракционного" кольца S=4
R. При дальнейшем
увеличении длины волны частицы в мишень попадают только частицы из
"дифракционного" кольца вокруг мишени, как показано на рисунке
10.2.1. Очевидно, что площадь "дифракционного" кольца S=4![]() Rr или, подставляя
значение r:
Rr или, подставляя
значение r:
S=2R![]() (10.2.2).
(10.2.2).
Эффективное сечение рассеяния будет в этом случае
![]() =Sw1w2
(10.2.3),
=Sw1w2
(10.2.3),
 |
 |
где w1 – вероятность попадания в мишень с поперечного и w2 – с продольного направления винтовой траектории частицы. Эти вероятности практически равны между собой:
w=2![]() R/
R/![]() (10.2.4),
(10.2.4),
т.к. при ![]() =2
=2![]() R вероятность
попадания в мишень любого фотона, ось винтовой траектории которого лежит в
пределах "дифракционного" кольца, равна 1. Подставив (10.2.4) и
(10.2.2) в (10.2.3) после некоторых преобразований найдем:
R вероятность
попадания в мишень любого фотона, ось винтовой траектории которого лежит в
пределах "дифракционного" кольца, равна 1. Подставив (10.2.4) и
(10.2.2) в (10.2.3) после некоторых преобразований найдем:
![]() =8
=8![]() 2R3/
2R3/![]() (10.2.5).
(10.2.5).
Эта формула применима при ![]()
![]() 2
2![]() R. При бесконечно
большой длине волны де Бройля частица мишени уже не "видит".
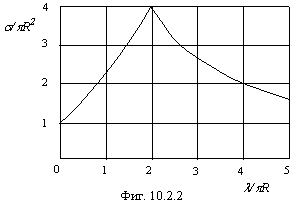
Эффективное сечение рассеяния в зависимости от длины волны по формулам (10.2.1)
и (10.2.5) представлено на графике (10.2.2) в безразмерных координатах
R. При бесконечно
большой длине волны де Бройля частица мишени уже не "видит".
Эффективное сечение рассеяния в зависимости от длины волны по формулам (10.2.1)
и (10.2.5) представлено на графике (10.2.2) в безразмерных координатах ![]() /
/![]() R и
R и ![]() /
/![]() R2. Максимальное
сечение составляет 4
R2. Максимальное
сечение составляет 4![]() R2
и совпадает с выводами квантовой механики. При
R2
и совпадает с выводами квантовой механики. При ![]() =0 сечение рассеяния совпадает с классическим
и составляет
=0 сечение рассеяния совпадает с классическим
и составляет ![]() R2.
R2.