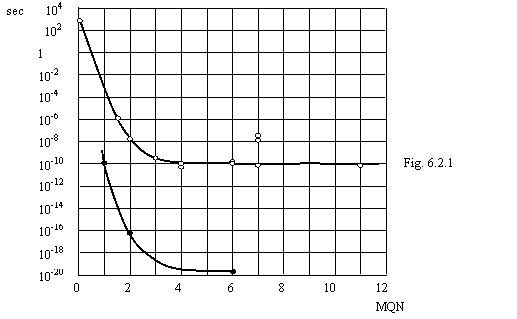6. STABILITY OF MICROPARTICLES
The microparticles
(atoms, atomic nuclei and elementary particles) are stable only in the ground
equilibrium condition. From any exited condition they spontaneously pass in the
ground nonexcited condition. And, the stronger is the excitation, the further
particle is from a ground state, the faster loses this excitation. Near to a
ground state of a microparticle can be rather long time (metastable state). An
exited state variously for miscellaneous microparticles. The atoms
"expands" at excitation - electrons leave from a nucleus, the
elementary particles on the contrary "contracts" - their
constituent’s moves on orbit of smaller radius and augment mass, therefore
ground state corresponds to decay of a elementary particle on stable component.
In atomic nuclei the ground state corresponds to a thermodynamic equilibrium
between number of protons and neutrons, and the degree of excitation is
determined by deviation from equilibrium composition of a nucleus, both in
that, and in other side.
The exited conditions
of atoms enough in detail are studied, therefore here on them to stop we shall
not be.
6.1. Neutron and nuclei of atoms
Neutron. From all known elementary
particles only neutron is in a minimum exited state, therefore metastable. The
difference of masses of a neutron and proton, which one falls on an electron
makes 1.29344 MeV (Physics of a microcosmos. "The Soviet
encyclopedia", М.,
1980, page 292). Under these data it is easy to find radius of orbit of an
electron around of a proton in a neutron, i.e. radius of the neutron under the
formula (6.5.3):
rn
= 2.81794092 × 0.5109991 / 1.29344 = 1.113283
fm (6.1.1).
Any other unstable
elementary particles, as a minimum, contain an electron with mass not less than
70.0252673 MeV.
In the literature
result a mean time of half-decay for a neutron from 624 sec up to 1040 sec.
Such dispersion is clear, since the gentle exited condition of a neutron is
removed by any gentle effect on it with transition in a ground state: n0
p++e-+
. Therefore is more preferential to trust to a
large half-life. If the mechanism of transition in a ground state for atoms
more or is less clear, the mechanism of transition in a ground state of
elementary particles - their decay, requires the special analysis.
That the neutron has
dissolved to stable particles, apparently, that it should be imparted such
energy, that the electron has gained an angular momentum 
instead of the moment ×
, where - fine
structure constant. As =m0 cr0, where m0 - mass
of a mobile electron, r0 - minimum radius of a screw
trajectory of a nonrelativistic electron, for decay of a neutron is necessary
to reduce electronic mass on:
1.29344
– 0.5109991 = 0.7824409
MeV
(6.1.2),
equal
electron-binding energy with a proton. This energy is contained in the itself
electron of a neutron, therefore spontaneous decay of a neutron is possible and
for this purpose it is not required energy consumptions from the outside.
The found correlations for a neutron are easy for confirming by
following calculation. Electrostatic energy obtained at approach of an electron
with a positive proton up to spacing interval rn = 1.113 fm
(6.1.1) according to the formula:
E = e2/rn
(6.1.3)
is peer 2.073×10-6 ergs, that correspond 1.294 MeV
and coincides a difference of weights of a neutron and positive proton
expressed in MeV.
Nuclei of atoms. In deuterium the electron is
retains with two protons, therefore energy 0.7824409 MeV already has not enough
for decay of deuterium and this isotope of hydrogen appears stable. For tritium
two electrons are retained by three protons. Time of half-decay 12.33 years.
Let's compare bond energy 1H3 = 8.48215 MeV and 2He3
= 7.71739 Мэв and we
shall look at a constitution of these isotopes on a figure 6.1.1.
|
|
|
|
|
|
At a radioactive
decay the nucleus of tritium will reject an electron and antineutrino and will
formed a stable nucleus 2He3 in which one electron is
retained by three protons. Is received, that in compared nuclei three protons
do not change the position and the connection between them remains to a
constant. Therefore difference in energies of connection of these nuclei is
conditioned only by bond energy of one electron with a proton:
8.48215 – 7.71739 = 0.76476 MeV (6.1.4).
Compares (6.1.2) and
(6.1.4) it is possible to make three important conclusions. 1. Energy of an
electron in tritium slightly does not suffice to become free (0.7824409 –
0.76476 = 17.6809 keV), therefore time of half-decay of tritium is very great
as contrasted to by decay of a neutron, and decay is possible only as a result
of fluctuations of heat motion of nucleones of a tritium nucleus. 2. Energy of
connection of electrons with protons in a nucleus practically is identical to
any nuclei and is poor for free decay of neutrons of a nucleus. Thus, the
nuclei of atoms introduce some similarity of metal inclusive "free"
electrons, some of them do not belong to a particular proton. 3. Any nucleus
can be esteemed as a system of protons, which one is contained definite
quantity of electrons with energy close 0,78 MeV everyone. The similar
consideration is convenient for analytical investigation of a nuclear
interaction.
At excess of protons
concerning equilibrium composition of a nucleus in it there should be electronic
- positron pairs. They arise at motion of an electron near to a proton and the
energy not less than 1.022 MeV is indispensable for this purpose. To an
electron inside a nucleus does not suffice for this purpose 0.24 MeV, therefore
transformation of protons in neutrons inside a nucleus is cumbered. In this
connection, 
-decay frequently is substituted by radiation
of protons or electron-capture on orbit of atom, proximate to a nucleus. Thus,
on stability of nuclei to a radioactive decay big effect is rendered by an
electrons and positrons concentration in a nucleus, which one, in turn, is
determined by a ratio of protons and neutrons.
Life time in inverse
proportion to deviation from an optimal structure for nuclei:
(6.1.5).
If we shall plot
relation of time of half-decay to number of exuberant or missing neutrons in a
nucleus of the relatively most widespread isotope of the given element, the
nucleus which one usually is steady with rare exception, we shall receive
sharply decreasing time of half-decay depending on this number. But our
relation will not be the smooth curve, and polyline, since at an even number of
exuberant or missing neutrons the strength of a nucleus considerably increases,
and at odd - drops.
|
|
|
|
|
|
Looking on the constitution of nuclei in the applicable chapters, we can at
once point the most gentle place of a nucleus, i.e. the strength of nuclei
concerning a radioactive decay is determined not in the whole nucleus, and dot
"dislocation" on a surface of a nucleus. If the nucleus is symmetric,
such place is impossible to point, therefore similar nuclei are stable. Last
problem, is necessary to answer which one here, concerns isotopes with huge
time of half-decay reaching billions of years. Official physics explains such
decays by "tunnel effect". If to use the official theory of a tunnel
effect for a considered case, it is necessary to operate with such digits,
which one are not stacked in frameworks of common sense, therefore there is a
necessity to give the single mechanism of a radioactive decay for any nuclei.
If the small additional energy is necessary for decay, the decay goes no
problem. But in rather strong nuclei of those isotopes, the structure which one
is almost peer optimal, the considerable energy is necessary for spontaneous
decay. An alone way "to collect" it for all nucleones of a nucleus
and to concentrate on "dislocation". Naturally, that it should take
place in stochastic process and for very short time, that the fluctuation was
not dispersed again. Besides for a small number of nucleones in a nucleus the
multiple repetition of this process can be demanded, with a condition that
during repetitions the exuberant energy of "dislocation" is not lost.
It reduces even stronger probability of decay, since "time of
half-decay" of an exited condition of dislocation it is not enough. The
probability of such event is insignificant, that it is possible to show by
simple calculations; therefore time of half-decay very sharply is augmented
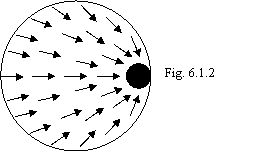
with increase of missing energy. Schematic in an ideal the considered event is
figured on a figure 6.1.2, where "dislocation" is indicated by a
black point, and the transmitting direction of impulses by nucleones is
indicated by arrows. From a figure it is visible, that it images practically
improbable event.
Life time of
elementary particles in inverse proportion to their main quantum number (MQN),
which one determines their exited condition. The decay of elementary particles
takes place as a result of transition in a ground state (decay up to stable
particles) at once or step-by-step, through intermediate conditions with
smaller MQN (smaller excitation). The spontaneous decay is always ensured with
internal large exuberant energy of components of a particle and does not
require external energy for the implementation.
|
|
|
|
|
|
On a figure 6.2.1 the relations of a life time of elementary particles to value
MQN are shown for particles inclusive simultaneously an electron and a positron
(black points) and remaining particles (white points). The first black point
concerns to a para-positronium MQN which one equally 1, since orbits of an
electron and positron will not formes one orbit. In baryons was allowed only
MQN of particles on orbit around of a proton, as proton does not influence a
life time of particles practically. For not quite clear reasons of a point for
kaons 
and 
lies above intended to them by curve of white points. The white
points correspond to particles (in brackets is indicated the value MQN): a
neutron (1/137), 
(1,5), 
(2), 
(3), 
(4), 
(4), 
(6), 
(6), 
(7), 
(11). The black points correspond to particles: a para-positronium
(1), 
(2),
(6).
Here there is no sense to esteem a life time of "resonances" since
they have time to be fall to pieces by not making and one revolution on orbit.
Thus, the notions of new physics about reasons of decay of nuclei and
elementary particles have found the endorsement.