5. RELATIVISM in NEW PHYSICS
The particle moved on a screw trajectory with speed V is not relativistic object, but its components always relativistic objects, as move on orbit of this particle with speed of light.
On known expression of new physics for an electron:
(5.1.1),
where 
=1.1576 cm2/sec. From (5.1) we
shall determine radius of a screw trajectory of an electron, which one is gone
with speed of light:
386.134×10-13 cm = 386.134 fm. (5.1.2).
From (5.1.2) completely clear there is a physical sense of value, which one official physics calls "a Compton wavelength of an electron":
=
1.0545727×10-27 / 9.109390×10-28 × 2.997924×1010 = 386.1594 fm = r0 (5.1.3).
It appears is that minimum radius of a screw trajectory of an electron, on which one it gains speed of light and becomes relativistic, i.e. instead of Vr=const, will follow mr=const for satisfaction of a law of conservation of angular momentum.
From (5.1.3) it is possible to update value =1.1576765 cm2/sec
for an electron. As any microparticles have an identical angular momentum on a
screw trajectory 
, for them:
(5.1.4),
Therefore for them minimum nonrelativistic radius of a screw trajectory (Compton "a wavelength" for the given particle):
(5.1.5).
From (5.1.5) it is visible, that
"wavelength" will be received only at multiplying both parts of
equality on 2
,
thus we shall receive a wavelength de Broglie for a particle driving with speed
of light. Thus, official physics does not understand, that such 
.
Official physics considers that the relativism starts there, where the energy of a particle becomes more "rest energy". New physics agrees with this statement:
(5.1.6).
Famous expression (5.1.6) anything diverse, as the
sum of kinetic energy of a particle of translational and tangential motion with
speed of light on a screw trajectory. I shall remind to the reader, that the
actual speed of a particle, for which one forward speed is peer to speed of
light, makes c
,
but it is impossible experimentally to determine this speed, while. If to take
into account, that 
, (5.1.6) will be copied as:
(5.1.7).
From (5.1.7) it is visible, that at radius of a screw trajectory the particle is less r0i is in relativistic area, and radius of its screw trajectory is inversely proportional of energy. To achieve zero radius, it is necessary to impart a particle indefinitely large energy, mass of such particle too will be indefinitely large. In this connection it is possible to guess, that with increase of power of particle accelerators will open all new and new particles with increasing masses, therefore it is better to not spend for satisfaction of this curiosity money all for nothing, while the present particle accelerators and cosmic rays will suffice.
Apparently, that (5.1.6) does not approach for nonrelativistic area, since the additional energy is spent for increase of speed, instead of on increase of a particle mass. Let's show, that one more expression of official physics:
(5.1.8)
Correctly for relativistic area. If the energy of a
particle E2>E1, is possible to record,
allowing, that 
:
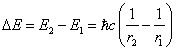(5.1.9).
Under the same conditions:
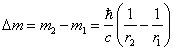(5.1.10).
By multiplying both parts (5.1.10) on c2, we shall receive (5.1.8).
Let's put without the evidence still pair of useful ratio:
(nonrelativistic area) and 
(relativistic area)
(5.1.11).
Apparently, that these ratio to equate each other it is impossible.
5.1.1. What energy corresponds to the formula E=mc2
Earlier (chapter 5.1) we have shown, that the famous formula:
E = mc2 (5.1.1.1)
is reflection of the greatest possible kinetic energy, which one has the body moving with speed of light. It is the sum of kinetic energy of a body, moving on a screw trajectory, in a longitudinal and tangential direction. Any relation to «rest energy» it has not, therefore it is necessary always to understand mass in this formula relativistic mass, which one at low speeds can practically coincide a rest-mass. In this book is clear shown, that mass of any particle is determined by its components, moving with light speed, therefore even for a «fixed» particle mass always relativistic, not relativistic mass does not exist. For orthodoxes it is considered, that the formula (5.1.1.1) expresses the greatest possible total energy of a body. New physics asserts, that it is the greatest possible kinetic energy of a body, but the potential energy of a body can be significant more.
Let's consider potential energy of electrostatic interplay of a proton with a nucleus of atom.
(5.1.1.2),
where e - elementary charge, Z - nuclear charge, r - spacing interval from a proton up to center of a nucleus.
Both nuclear charge, and spacing interval from a proton up to center of a nucleus we shall express through nuclear mass.
In chapter 12 is shown, that the internal part of any
nucleus represents a similarity of crystal lattice in clusters by which one
there are -
particles, therefore nuclear mass expressed through its charge will be
approximately (without the registration of a defect of mass) is peer:
(5.1.1.3),
where mp - mass of a proton, mn - mass of a neutron.
The connection of nuclear mass with r is obvious:
(5.1.1.4),
where 
- nuclear density of matter (1014
g/cm3).
Substituting (5.1.1.3) and (5.1.1.4) in (5.1.1.2), we shall discover:
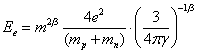(5.1.1.5).
Let's substitute numerical values of constants in a system CGS in the formulas (5.1.1.1) and (5.1.1.5).
E = 8.9875×1020× m (5.1.1.6),
Ee = 2.06265×1010× m2/3 (5.1.1.7).
Let's substitute in (5.1.1.6) mass of a proton mp = 1.6726×10-24 g, then its «rest energy» will make 1.5032×10-3 ergs. By substituting this value in (5.1.1.7) we shall discover, what there should be a mass of a supernucleus, that the proton on its surface had potential energy of equal its «rest energy»:
mZ = 1.7447×10-9 g (5.1.1.8).
New physics guesses a capability of formation of supernuclei of mass up to 6.63×1034 g (chapter 29.7.1), therefore «the rest energy» under the formula (5.1.1.1) can make only insignificant part of a total energy of a particle. Here we once again can be convinced that official physics manipulates some concepts, not having clear representation that substantially is contained in these concepts. Now become clear those grandiose power phenomena on periphery by the Universe, it is impossible to explain which one outgoing from official representations, bound with the formula 5.1.1.1.
Here too it is necessary to open physical sense of «rest-mass» and «rest energy»:
E = m0c2 (5.1.1.9).
In the theory of elementary particles is shown, that all they consist in the final accounting of an electronic neutrino and antineutrino having in a free condition minor mass. At formation of a particle half of obtained energy goes on increase of mass (it becomes equal «to a rest-mass»), and half on bond energy. Energy of connection on a virial theorem numerically will be peer to energy of universal repulsing:
Erep = m0c2/2 (5.1.1.10),
therefore general energy will be peer (5.1.1.9). The formulas (5.1.1.9) and (5.1.1.10) are valid only for particles having a potential well of gravidynamic interplay. This potential well will be formed at interplay of components from homomatter (matter or antimatter). At formation of a particle from heteromatter (matter - antimatter) the potential well misses (photon), therefore their energy is determined by the formula (5.1.1.1) and they always movements in vacuum with speed of light.
Energy under the formula (5.1.1.9) is a latent energy of a particle, which one in any way herself does not exhibit so long as we save its integrity. Similarly intranuclear energy also is latent so long as a nucleus invariably.
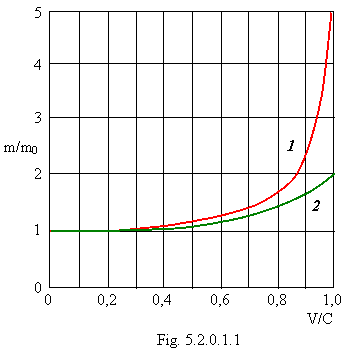
5.2. Relativistic growth of a particle mass
 |
On a figure 5.2.1 the relation of relativistic mass to a rest-mass of an electron is shown depending on its speed in fractions from speed of light. The full curve corresponds to the known formula of a relativity theory:
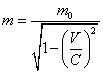(5.2.1),
the experimental points are obtained in 1901-1909. The graph is borrowed from the book J.B. Marion "Physics and physical world", "World", М., 1975, page 30.
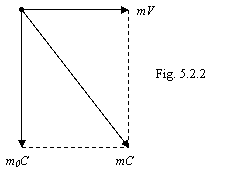
Now we shall show that the real situation with relativistic growth of a particle mass is much more complex, than it is represented on a figure 5.2.1. The formula (5.2.1) is easy for receiving from the following scheme of impulses (figure 5.2.2).
This scheme is suitable for a immobile electron,
which one only we are be about to move to the right on a figure. Two neutrinos
on orbit of an electron everyone in mass m0/2 already move
with speed of light (as on orbit of any elementary particles), therefore any
attempts to displace an electron result in relativistic increase m0.
Thus the motion of an electron as whole on a screw trajectory of any
contribution in relativistic increase of mass does not give so long as radius
of this trajectory will not become equal r0 under the formula
(5.1.2). Therefore on an initial segment of the graph of a figure 5.2.1 up to
forward speed of an electron 
the formula (5.2.1) will be valid. At the
indicated speed the electron becomes relativistic, since the vectorial sum to
its translational and tangential velocity on a screw trajectory is peer of
speed of light. This moment is indicated by a dagger on a figure 5.2.1.
Here there is an interesting collision arises. By the
formula (5.2.1) to use already it is impossible, the concept any of an
alteration of speed also is unsuitable in relativistic area. Therefore we shall
take advantage of a ratio (5.1.8). The change of energy will formally was
equally: 
E=mV2
since is necessary to expend identical energy mV2/2 on a
translational motion and tangential. Change of mass: m=m-m0. Then
(5.1.8) will give:
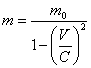(5.2.2).
The obtained formula demonstrates, that when the electron on a screw trajectory becomes relativistic, the relativistic increase of mass takes place much faster that an angular momentum of an electron on a screw trajectory in 137 times more its own moment. All would be just so, if value m0 on precisely to the same law simultaneously did not decrease, which one assigns expression (5.2.1), i.e.:
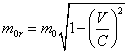(5.2.3),
where m0r - relativistic "rest-mass" of an electron in this area. From (5.2.3) it is visible, that in a limit, when the speed of an electron on a screw trajectory will reach speed of light, "rest-mass" of an electron will become zero. Physically it means, that at one revolution of an electron on a coil of a screw trajectory a neutrino inside an electron commit too one revolution, i.e. an electron always rotated to an axis of a screw trajectory by one side, as moon to the Earth. It provides a condition, that the speed of particles on orbit did not exceed speed of light. As the rest-mass of components of a relativistic particle becomes to equal zero point to find bond energy of a particle, it is necessary from its rest-mass to subtract rest-masses of all components. To take into account above set up, the formula (5.2.3) should be substituted in numerator (5.2.2). Thus with increase of speed numerator will decrease, and the denominator decreases faster. After formal transformation in the total again we shall receive the formula (5.2.1), but now motion picture of a relativistic electron has become clear and the arisen collision has vanished.
When the speed of an electron becomes of equal speed
of light, radius of a screw trajectory of an electron is peer on (5.1.2)
386.1594 fm. Thus the formula (5.2.1) becomes completely unsuitable for the
description of motion of an electron. Really, from expression for an angular
momentum of an electron in relativistic area: 
let's discover m
and we shall substitute in (5.2.1). After transformations V/c=0 or V=0,
that is dispossessed of physical sense.
 |
Here it is necessary to mark, that the formula (5.2.1) by us is obtained from only classic summation of electron impulses on a figure 5.2.2 and any relations to the so-called factor of the Lorentz
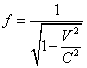has not. Has not relation and to a
special relativity theory. Besides, in this chapter is clear shown, that the
formula (5.2.1) has a restricted field of application up to a forward speed of
an electron 
and further
becomes inapplicable. Nevertheless, official physics applies the factor of the
Lorentz, where it is necessary and it is not necessary, not understanding true
physical phenomena latent behind this factor. The true reason of increase of
mass of a driving particle is, that component this particle (for an electron it
is a neutrino, see chapter 7.2) always moves with speed of light, therefore for
fulfilment of a law of conservation of angular momentum mass grows in inverse
proportion to radius of orbit of components of a particle.
Again we are addressed to a figure 5.2.1. With
increase of forward speed of an electron its tangential speed on coils of a
screw trajectory was augmented also. When both speeds have reached value , the total trajectory
speed has become of equal speed of light. At increase of mass radius of the
electron has decreased and here all clear. In a considered point of a figure
5.2.1 m=1.41m0, V=C/1.41 is multiplied: 
where r0
– 386.134 fm. At further increase of forward speed (up to 0.866×С) radius
of a screw trajectory decreases in 2 times, from this value goes on increase of a tangential
velocity and it becomes of equal speed of light, and still goes on increase of electronic mass
and it becomes 2m0. From this moment the increase of forward
speed of an electron results in decreasing radius of a screw trajectory
(«wavelengths» of an electron) and applicable increase of mass mr=const.
The equation (5.2.1) connections of mass of a body with its speed becomes
unsuitable, and electron completely relativistic. Further more correctly to
link electronic mass to its «wavelength» (energy or radius of a screw
trajectory) instead of with forward speed. Thus, the area of increase of
electronic mass from 
Up
to 2m0 is transition region from Vr=const to mr=const
and it is indicated on a figure by 5.2.1. cyan colour.
At forward speed of a particle V = 0.866C it, as whole, is gone on a screw trajectory with a tangential velocity, equal speed of light, therefore its own angular momentum becomes to an equal angular momentum on a screw trajectory in not relativistic area, and the former own angular momentum becomes to equal zero point and together with it will become to equal zero point and former «rest-mass» m0. Here we as though have recreated a particle from components with zero «rest-mass» therefore «new» rest-mass again will be peer m0 and the formula (5.2.1) again will become valid.
5.2.0.1. Relativistic mass macrobodies
On a figure 5.2.0.1.1 Curve 1 are demonstrated with relativistic growth of mass of a separate microparticle depending on its speed pursuant to the formula:
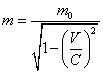(5.2.0.1.1).
This formula is obtained as a result of the analysis of impulses of components of elementary particle (chapter 5.2). The free elementary particle is moves on a screw trajectory in space in such a manner that the orbital plane of its components is always perpendicular to a traveling direction. It is outcome of gravidynamic self-effect of a particle.
 |
In macrobody there is no capability to analyze a direction of impulses of each elementary particle from which one consists macrobody, since the orbital plane of components of particles is arranged chaotically and is not perpendicular, generally, traveling direction of macrobody. Freely to be turned in space it can not because of interconnection in a body. The plane of very many orbits in the given moment appears almost parallel to a traveling direction of a body and in this case relativistic growth of mass of such particles does not occurs, since on one half of orbit mass grows, and on other drops in the same way. Therefore similar particles practically do not introduce the contribution to relativistic growth of mass macrobody. Besides both for free elementary particles, and for macrobody, the motion them on a screw trajectory on those to the causes does not influence growth of mass, since the screw motion represents independent from each other translational motion and perpendicular to him tangential motion. Therefore relativistic growth of mass of any bodies determines only of translational component of their motion.
For «fixed» macrobody its mass is determined by the sum of weights of all particles from which one a body consists. Each of them represents components rotated with light speed around of common center of gravidynamic interaction. Half of energy of gravidynamic attraction of components at formation of a particle is spent for universal energy of a repulsion, equal mi×c2/2, where mi - particle mass, and second half is spent for bond energy of components, which one pursuant to a virial theorem also is peer mi×c2/2. If now to find common energy of deleting components of each particle on perpetuity (equal energy of gravidynamic attraction) and to summarize it on all particles of a body, we shall receive the famous formula of energy of «rest» of a body: E0 = m0c2. Apparently, that at motion of macrobody to this energy it is necessary to add a kinetic energy of translational component of motion: Ek = mV2/2 to receive relativistic energy macrobody: mc2=m0c2+ mV2/2. Then the relativistic growth of mass macrobody depending on forward speed it will be determined by the formula:
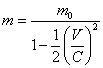(5.2.0.1.2),
the graph by which is
figured (2) on a figure 5.2.0.1.1. Pay attention that the
relativistic growth of mass macrobody at its speed equal speed of light can not
exceed 2m0. This growth will become infinite only at motion
of macrobody with speed 
. Just this speed is the greatest possible running speed of
bodies. Just with this speed the photons and particles with «zero rest-mass»
move if to add up their translational and tangential velocity on a screw trajectory.
It is interesting, what the Einstein and his followers thinks in this reason?
5.2.1. Light speeds in new physics
In new physics of notions about light speeds differ from official.
In chapter 7.3 the concept of maximum speed is entered, which one exceeds speed of light slightly in vacuum, therefore sometimes it is more useful to mean just maximum speed.
In chapters
4-10 is shown, what the components of elementary particles move on circular
orbits with light limiting speed, therefore principle of conservation of moment
of momentum requires increase of a component mass with decreasing of radius of
its orbit so that product m×r remained to a constant. Therefore on a circular
orbit the particle can move with maximum speed. As all free bodies in the nature
move on a screw trajectory, with increase of a running speed radius of this
trajectory decreases, that is a reason of increase of a body mass. Apparently,
that if the body could achieve limiting forward speed, radius of a screw
trajectory would become peer to zero point, and mass of a body infinite. From
here follows, that is impossible to achieve maximum speed at translational
motion. At the same time speed of a body on a coil of a screw trajectory is the
vectorial sum translational and tangential velocity and easily can overcome a
boundary of maximum speed, coming nearer to value C,
where C - speed of light.
5.2.2. Relativistic growth of electronic mass on atomic orbit
Official physics considers the formula of relativistic growth of mass suitable for all cases. New physics has shown, that at orbital motion of an electron its speed can reach speed of light at radius of orbit around of a nucleus r0 = 386 fm (see chapter 5.1). At further decreasing of orbit radius the speed of an electron remains invariable, and mass grows under the formula
:
(5.2.2.1),
where: m - relativistic electronic mass, me - mass of a not relativistic electron, r - orbit radius.
 |
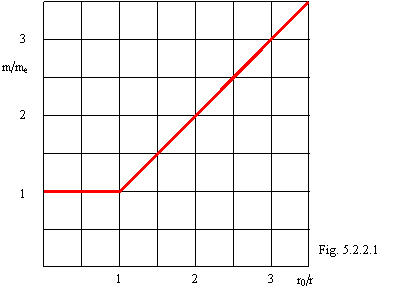The graph of relativistic growth of electronic mass on orbit is shown on a figure 5.2.2.1 (compare to a figure 5.2.1).
Now it is
interesting to look, what should be nuclear charge of a hydrogen-like atom,
that the electron had orbit of radius 386 fm. For this purpose we shall take
advantage of the formula (2.3) for radius of orbit in a ground state from
chapter 2: 
.
Though it is unduly from the point of view of physical sense, we shall multiply
numerator and denominator on me. Then in numerator there will
be a square of angular momentum of an electron, but against mathematics we thus
shall not sin:
(5.2.2.2).
From (5.2.2.2) we shall discover Z:
(5.2.2.3).
But 
, where ra - radius of first
Bohr orbit, therefore:
(5.2.2.4).
By substituting in (5.2.2.4) numerical values, we shall discover Z = 137.
Thus, the relativistic growth of electronic mass on orbit of any conceivable atoms is impossible, therefore official physics makes the next error, when takes into account this growth.
Numerical concurrence of the found nuclear charge with reverse value of a fine structure constant not incidentally. The business that a running speed of an electron on orbit of the Bohr in 137 times is less than speed of light. To achieve speed of light, it is necessary radius of orbit of an electron to reduce in 137 times, then pursuant to the formula (5.2.2.2) nuclear charges need to be increased in 137 times.
Let's suspect, that we imparted to electron such large energy, that radius of a screw trajectory it has decreased that has coincided with classic radius of the electron. In this case speed of an electron, starting from radius instituted by expression (5.1.2) does not vary any more and is peer C, and for fulfilment of a law of conservation of angular momentum the product mr should remain a constant:
(5.3.1),
whence:
=1.0545727×10-27/2.81794092×10-13×2.997924×1010=1248.314×10-28 g
(5.3.2).
Rest-mass of an electron m0=9.109390×10-28 g. Therefore, electronic mass on such orbit applicable orbit of elementary particles will be increased in:
m/m0=137.03596 times (5.3.3),
i.e. corresponds to value, return fine structure constant (137.0359895). If (5.3.2) to translate in power units (5.609586×1026 MeV/g), we shall receive value of unit of a main quantum number (MQN, see elementary particles) in power expression:
12.48314×10-26 × 5.609586×1026 = 70.02525 MeV. (5.3.4).
It is possible to count up electronic mass at reduction of radius of a screw trajectory up to re:
m = 0.5109991 × 386.1594 / 2.81794092 = 70.025281 MeV (5.3.5).
The most precise power value of unit MQN can be received, by multiplying a rest energy of an electron on reverse value of a fine structure constant 1 MQN = 70.0252673 MeV.
As the particles in a free condition have an angular
momentum , apparently, that the "exited" quantum conditions of the
given particle will be aliquot to this value. Therefore, the energy levels of
elementary particles will be aliquot 70.025 MeV or half of this value, if the
orbital angular momentum any of a component is peer /2.
5.4. Technique of calculation of radiuses of orbit, bond energy, magnetic moment and masses of elementary particles
How to find bond energy of a elementary particle, was set up in section 5.2, here only it is necessary to add, that in bond energy it is necessary to allow also for electrostatic interplay of components of a particle, though it by an essential image does not influence on bond energy.
The common angular momentum of a particle as a whole (main quantum number MQN) N is peer to the sum of moments of components on orbit of this particle:
(5.4.1),
therefore computational mass of any particle on orbit to equal radius of an electron is peer:
mcal=N×70.0252673 MeV (5.4.2).
If the value mcal differs from a substantial particle mass more, than on 35 MeV, it means, that our suppositions about a constitution of a elementary particle require elaboration or insecurely is determined MQN.
Comparing a calculating value of mass with experimental value, it is possible to make conclusions about additional repulsing or attraction of components, which one augments or reduces radius of orbit and results in decreasing or increase of a real particle mass.
Radius of any elementary particle
(5.4.3),
where m - experimental particle mass. If it is a rest-mass of a particle, (5.4.3) will give updated value of radius of orbit of components of a particle, on which one it is possible to judge interplay of these components or return substitution in (5.4.3) to find precise value of a particle mass.
Apparently, that the majority of elementary particles will have radius, close classic radius of an electron. For calculations in a microcosmos it is convenient to use unit of spacing interval: 1 fm = 10-13 cm and mass unit expressed in MeV: 5.609586×1026 MeV/g. 1 MeV = 1.60206×10-6 ergs.
Let's substitute these values in (5.4.3) and we shall receive expression, where mass is expressed in MeV, and radius in fm, is convenient to use which one for any component of a particle or particle as a whole:
(5.4.4).
Magnetic moment of particles calculate under the formula:
(5.4.5),
where 
- magnetic moment in an erg×gauss-1,
e - electric charge in units of CGSE, m - particle mass, c
- speed of light. By substituting in (5.4.5) for relativistic
area and 
for not relativistic area, after transformation, we shall discover
expressions, which one do not depend on masses of particles:
(5.4.6),
for not of relativistic particles and:
(5.4.7)
for relativistic particles.
For example, for an electron in not relativistic area
on (5.4.7) 
=0.9274015×10-20
ergs×gauss-1. To this value still it is necessary to add an
own magnetic moment of an electron, but as the neutrino which is formed an
electron relativistic, is necessary to use (5.4.7) substituting in it classic
radius of an electron: 
=0.006767576×10-20
ergs×gauss-1. Piling both values, we shall receive: 
= 0.934169×10-20
ergs×gauss-1. The relation of a magnetic moment of a mobile
electron to a magneton of the Bohr will be: / = 1.007297271. In process of increase of
speed of an electron radius of a screw trajectory decreases, the own rotation a
neutrino in an electron also is slowed down. At achievement of minimum not
relativistic radius of a screw trajectory 386.1594×10-13 cm
for one revolution of an electron on a trajectory a neutrino it also makes one
revolution, i.e. the electron is gone as a solid and the additional
contribution to a magnetic moment does not introduce. Then from (5.4.7): 
= 0.9274017×10-20
ergs×gauss-1. In this case relation of a magnetic moment of an
electron to a magneton of the Bohr will be: / = 1.0000002. Thus, the magnetic moment of an
electron with increase of its speed drops and when it becomes relativistic, its
magnetic moment coincides a magneton of the Bohr. At further increase of energy
of an electron its radius of a screw trajectory is inversely proportional of
energy, accordingly and the magnetic moment will decrease sharply. For example,
at energy of an electron 70.0252673 MeV (radius of a screw trajectory is peer
to classic radius of an electron), its magnetic moment on (5.4.7) will be: =0.006767576×10-20
ergs×gauss-1, i.e. to coincide an own magnetic moment of a
mobile electron. Then the relation of a magnetic moment of such electron to a
magneton of the Bohr will make: /=0.00729735. Thus, the magnetic moment of
particles is not a constant, and varies depending on radius of a screw
trajectory of a particle or radius of orbit in a structure of other particles.
The experimentally
retrieved magnetic moment of an electron is a little more magneton of the Bohr in 1.0011616 times. Official
physics considers a magnetic moment of an electron as abnormal (it should be
peer to a magneton of the Bohr) and attracts for its explanation of notions
about interplay of an electron with virtual particles of vacuum: "Abnormal
magnetic moment of an electron. The radiospectroscopic researches have shown,
that the magnetic moment of an electron is not peer accuracy to one magneton,
and it is few more. The quantum electrodynamics has shown, that the increase of
a magnetic moment of an electron is obliged to interplay of an electron with
vacuum (physical space)". N.I. Kariakin etc., "Brief reference book
on physics", "Higher School", М.,
1962, page 354.
For new physics is apparent, that the electron, moved
on a screw trajectory, with an angular momentum will create a
magnetic moment, equal magneton of the Bohr a plus a part of an own magnetic
moment of an electron (with an angular momentum 
). If the electron
moved on a screw trajectory with light speed (as a photon), it would be turned
to an axis of this trajectory always by one side, i.e. would move as a solid.
In this case own magnetic moment of an electron would give the zero
contribution to the common moment, since blade-swept by charges a neutrino the
area is peer to zero point. In this case magnetic moment of an electron would
be in accuracy peer to a magneton of the Bohr. As a neutrino in an electron
moves with light speed, and electron on a screw trajectory with significant by
smaller speed, a trajectory separate the neutrino will represent a variety of
an epicycloid with blade-swept area of "electric current" 
, instead
of 
, and common magnetic moment to correspond experimentally retrieved.
This value coincides the correction of J. Schwinger to a magnetic moment of an
electron: (/2).
If we mechanically have added up a magnetic moment of
an electron on a screw trajectory with an own magnetic moment, equal /137.0391=0.0072971, in the total would
receive the overstated common moment =1.0072971. By the way to tell, the magnetic moments of
the majority of particles "are anomalous", for example, for a neutron
and proton. And irregularity last is not stacked in theoretical notions of
orthodox physics, designed for an electron, that serves endorsement of an
inaccuracy them.
With a magnetic moment of an electron it is necessary to be disassembled more in detail, since the notions of new physics differ from official physics in this problem sharply. Let's consider in the beginning nonrelativistic electron. For this case we shall use the formula (4.5) on which one a magnetic moment of an electron driving on a screw line, will be:
(5.4.8),
where V - tangential velocity of an electron (equal translational), C - speed of light, e - elementary charge, R - radius of a screw trajectory. An angular momentum of an electron on a screw trajectory:
(5.4.9),
where m0 - rest-mass of an electron. By substituting (5.4.9) in (5.4.8), we shall discover, that the magnetic moment of an electron in this case is peer to a magneton of the Bohr:
(5.4.10).
Now we shall consider a relativistic electron. For this case we shall use the formula (4.4). The similar calculations, allowing, that thus
(5.4.11)
will give:
(5.4.12),
i.e. the magnetic moment of a relativistic electron 
already will depend on its
mass and to decrease with increase of energy of an electron. The formula
(5.4.12) can be received differently. The relativistic electron is gyrated on a
screw line as a solid, making one revolution about the own axis for one
revolution on a screw trajectory, because of impossibility component it a
neutrino to move with superlight speed. Therefore it is possible to record for
the first (outside) neutrino, allowing, that the charge a neutrino is peer e/2:
, where r - radius of an electron. For the second (internal)
neutrino: 
. The sum of the moments will be 
, whence,
expressing R through an angular momentum of an electron (5.4.11) we
shall receive (5.4.12). It is necessary to mean, that in a relativistic
electron not only the wavelength de Broglie (radius and step of a screw
trajectory) decreases, but the sizes of the electron decrease also, therefore
magnetic moment of a relativistic electron is not fixed value, as it is
represented to official physics. Now we shall discover an own magnetic moment
of a nonrelativistic electron, allowing, that a neutrino in an electron moves
with speed of light:
(5.4.13).
Substituting in (5.4.13) values
(5.4.14)
- fine structure constant and classic radius of an electron
(5.4.15),
let's discover 
, i.e. the own magnetic
moment of an electron in 137 times is less than a magnetic moment on coils of a
screw trajectory. The own mechanical moment of an electron, apparently, is
peer:
Sown= m0Cr0 (5.4.16).
The ratio of a magnetic moment (5.4.13) to mechanical (5.4.16) will make:
(5.4.17).
By substituting (5.4.15) in (5.4.13) and obtained
expression for own
in (5.4.17), we shall discover:
(5.4.18).
The ratio of an own mechanical moment (5.4.18) to a
mechanical moment on a screw trajectory gives expression (5.4.14),
that is natural. The formula (5.4.18) gives the answer to a riddle of a genesis
of electric charge 
- electric charge directly
is connected to presence of an angular momentum neutrino in an electron or
positron, at the end, with presence of an angular momentum the itself neutrino.
Thus, the common magnetic moment of a "thermal" mobile electron equal
(1+) = 1.007297 is more, than officially
recognized 1.0011616
and obtained from the spectroscopic data (the almost relativistic electron) and
decreases in inverse proportion to energy of an electron. The experimental
endorsement it will deliver a modern quantum mechanics in an inconvenient
situation.
5.5. Electron (positron) and neutrino
The constitution of an electron (positron) is already
reviewed enough in detail. If the electron is on orbit of any particle, it
saves value of an angular momentum of a mobile electron and if an
electron one on orbit, together with it on this orbit there is an antineutrino
or neutrino for a positron (for example, neutron, muons). If radius of orbit is
peer to classic radius of an electron, its mass increases up to 70.025 MeV.
Thus the size of the electron on such orbit decreases in 70.0252673 / 0.5109991
= 137.0359895 times and becomes equal 2.81794092 / 137.0359895 = 0.02056351 fm.
Electronic neutrino which is formed an electron exact as decrease in the sizes,
and mass everyone a neutrino becomes equal 35.01263365 MeV (/2). In
comparison with a mobile electron and free neutrino (ground state) their
condition on orbit with radius to equal classic radius of an electron is their
first exited state N=1. At N=2,3,4… the electronic mass will be
augmented in a number of times, aliquot 70.0252673 MeV, and mass a neutrino
will be increased in a number of times, aliquot 35.01263365 MeV. As the law of
conservation of angular momentum requires that the product mr should
remain to a constant, the radiuses of orbits depending on MQN will be
determined by expression:
(5.5.1).
From (5.5.1) it is visible, that at N=0
(ground states) radius of motion of a particle indefinitely large, but at
preservation of an angular momentum is (customary ), the running
speed will be peer to zero point. At indefinitely large N (indefinitely
large mass and energy of a particle) rN 
0.
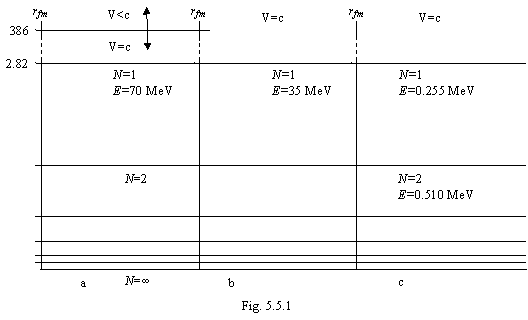
The formal value MQN is easy for finding, by sectioning mass of a particle, interesting for us, (in MeV) on the power contents of unit MQN (70.0252673 MeV). If is received close to the whole value N, quantity a neutrino in a particle even, if close to half-integer value - is odd. However, actually energy levels of particles almost never obey in accuracy to expression (5.5.1). The differences will small and be conditioned by electrostatic interplay and miscellaneous interplay homomatter (matter - matter, antimatter - antimatter) and heteromatter (matter - antimatter). Thus, the indicated interplays sliver levels of energy instituted by expression (5.5.1) on series of sublevels depending on a concrete constitution of a particle and the value N, as at miscellaneous N the components are on miscellaneous spacing interval from each other, and their interplay is not proportional to spacing interval.
As for orbital motion of a particle with speed of light:
(5.5.2),
that:
(5.5.3),
where m - particle mass on orbit of radius r, and m0 and r0, accordingly, particle mass and radius of orbit of comparison, on which one these values are known or formally are determined, for example, under the formula (5.1.5). Using (5.5.3) always it is possible to introduce the indispensable corrections taking into account of a precise position of a power sublevel. For example, mass of a muon 105.658387 MeV. Through 2.19703×10-6 sec it is disintegrated with probability about 100 % on an electron, electronic antineutrino and muonic neutrino. By sectioning mass of a muon on 70.0252673 MeV, we shall discover formal value Nf=1.508861. Computational mass of a muon from table 5.5.1 will be:
mm = 70.0252673 + 0.25549955 + 35.01263365 = 105.2934005 MeV.
Whence calculating value MQN: Nm = 1.503649. In (5.5.3) it is possible to use ratio formal and calculating value MQN:
r = 2.81794092 × 1.503649 /1.508861 = 2.80820702 fm.
We have received updated radius of a muon. It slightly less than classic radius of an electron, that indicates some attraction between components of a muon. The increase of radius would indicate some repulsing. With accounting of obtained radius of orbit (5.5.3) will give value of mass of a muon precisely conterminous with experimental value. In the same way find radiuses of any other elementary particles in a state of rest. At motion of a particle, as whole radius it decreases and easily to count up it for relativistic and ultra relativistic particles.
The characteristics of an electron (positron) and neutrino are shown in table 5.5.1.
Table 5.5.1.
|
Particle |
Electron |
Electronic neutrino |
Muonic neutrino |
|
Angular momentum of a free particle |
|
|
|
|
Mass of a free particle, MeV |
0.5109991 |
4.828558 eV
|
661.68623 eV
|
|
Mass in a structure of an electron, MeV |
- |
0.25549955 |
- |
|
Mass at orbital motion with radius of an electron N=1, MeV |
70.0252673 |
0.25549955 |
35.01263365 |
|
Mass at N=2, MeV |
140.0505346 |
0.5109991 |
70.0252673 |
|
Radius of a free particle, fm |
2.81794092 |
depends on energy |
depends on energy |
|
Radius of a bound particle |
Is inversely proportional to mass |
Is inversely proportional to mass |
Is inversely proportional to mass |
The notice to table 5.5.1. To find mass a free neutrino, it is necessary to take into account that they move with speed of light in a free condition then, for example, mass the electronic neutrino will be:
0.25549955 / 137.035989 × 386.134 = 4.828558×10-6 MeV,
and mass a muonic neutrino:
35.01263365 / 137.035989 × 386.134 = 661,686230×10-6 MeV.
Earlier was retrieved, that radius a free electronic neutrino is peer to half of radius of a screw trajectory it.
On a figure 5.5.1 the energy levels of an electron (а), muonic neutrino (b) and electronic neutrino (c) are figured depending on N.
 |
5.5.1. Superfluidity and superconductivity
As the angular momentum of an electron on coils of a screw trajectory can not vary - it or is, or it is not present, at super-low temperatures (or in requirements of forfeiting of an electron of its angular momentum) we should watch discontinuous jump of properties of substances one way or another bound with presence of mobile electrons. At standard temperatures of such effects it is possible to reach, depriving electrons of an opportunity to move on a circular helix, for example, in hyperfine conductors, radius which one is significant less of wave length de Broglie of an electron at given temperature. The example of such superconducting framework with a current is served a molecule of a benzol.
Superfluidity and superconductivity from a point of view of new physics have the same reason - forfeit by particles of a moment of momentum on coils of a screw trajectory.
In first case is losses of the moment atoms of
helium, and in second - electrons (=0). The question is who to
transmit this moment.
The atoms of helium transmit to its atoms of walls of
a vessel, in which one there is a fluid helium, phase change of the second kind
therefore is watched and in fluid helium there are as though two fluids, for
which one the motion of atoms is basic variously. In helium I they move on
segments of screw lines, and in helium II - on direct. Thus, not contradicting
the double-fluid model superfluidity of a modern physics, most adequate to
experiments, the new physics makes the same deductions, not attracting an
official quantum mechanics. The transition of fluid helium in a superfluidity
state is not accompanied by heat effect (phase change of the second kind or 
-transition), since at
losses by atom of helium of an angular momentum on a screw trajectory the given
atom becomes "cold", but its energy is transmitted to adjacent atoms
and in the whole heat effect is not watched because of the law of conservation
of energy. However, as the helium in a state of superfluidity represents an
intermixture "cold" (with absence for atoms of an angular momentum)
and "hot" (with an angular momentum, maintained for atoms) fluid, the
mechanocaloric effect is watched. At flowing out HeII from a vessel
through a narrow capillary tube in a vessel temperature is increased and, on
the contrary, in a place of an inflowing HeII from a capillary tube in
other vessel there is a cooling. At transition of helium in a superfluidity
state, its thermal conduction is incremented, approximately, in 106
times and the mechanism of a thermal conduction differs from customary to many
indications. This effect also is obvious: the atoms dispossessed of an angular
momentum are look-alike to electrons of superconductivity.
The enunciated reason of a superfluidity of helium enables to influence this effect by the additives in fluid helium of molecules, which one as a whole or their parts would like hook a moment of momentum of atoms of helium. Apparently, what to receive effect of superfluidity at standard temperatures it is impossible, since the potential receivers of an angular momentum take it for not so much atoms, how many award with it. Apparently, only by gear transmission of atoms through channels, the diameter which one certainly is less than diameter of a screw trajectory it is possible to achieve any successes. That concerns also superconductivity in case of a motion of charged particles. In this connection there is a sense to put forward a hypothesis, according to which one in biological objects for a durable memory the insular electric currents of a superconductivity implemented at standard temperatures in molecular channels are responsible. For 3He the connection between atoms is stronger, than the connection between atoms 4He at the expense of a uncompensated of magnet moment of atoms, therefore losses of an angular momentum by atoms 3He is impeded, since they should interact at once with many neighbors with major effective mass (on measuring a heat capacity meff=3.1m). Therefore transition temperature 3He in a superfluidity state is lower (0.01 0К), than for 4He (2.1 0К). For explanation of a superfluidity 3He the official physics resorts to formation of superconducting pairs already from atoms 3He, considering their fermions. Apparently, that at formation of superconducting pairs the system as a whole transfers in a more profitable energy state and this process should be accompanied by a heat liberation, i.e. the phase change of the first kind should be watched, that does not correspond to experimental data.
The electrons
transmit it’s the moment to crystal defects or atoms of
"impurity", and also the atoms of the basic crystal lattice, if do
not have anything applicable more. Therefore transition temperature in a
superconducting state of monocrystals of pure elements is very small. Physics
of a microcosm, "Soviet encyclopedia", М.,
1980, page 335.
From a point of view of orthodox physics the
requalification of electrons from individualist-fermions (=1/2) in
the collective farmers-bosons (=0) is completely impossible
while the new physics considers, that the electrons, indiscernible on an
angular momentum, (for all =1) are distinctive (part
have =1, and part =0), i.e. state "of
electronic gas" at a superconductivity similarly to double-fluid model of
a superfluidity.
The effect of the Josephson on notions of new physics
directly confirms losses by electrons of a moment of momentum in an appearance
of superconductivity. The effect is watched at passage of a superconducting
current through a layer of a dielectric or layer of metal in a normal state or
in superconductors with waist (point contacts). If the current exceeds some
critical value, there is a voltage drop U and the photons with energy h
=2eU are
radiated. The official physics considers, that the photons are radiated by
superconducting pairs of electrons, which one are excited, and then radiate,
transferring in a normal state. Such notion calls severe declaiming: 1. On a
segment of a voltage drop the superconductivity misses, therefore
superconducting pairs on this segment miss. 2. It is vague, how two electrons
of a superconducting pair simultaneously can radiate one photon with summary exuberant
energy of both electrons. 3. Allowing, that distance between electrons of a
superconducting pair makes 10-4 cm, between them there is a huge
amount of other electrons belonging to other pairs. In this case radiation by a
given superconducting pair of a photon with energy 2eU seems even more
improbable. 4. As the superconducting pairs all time fade and occur again, is
not clear, how again born pair perceives an exited state previous, that in the
total to accumulate exuberant energy 2eU. The new physics explains a
Josephson effect simply and without inconsistencies.
 |
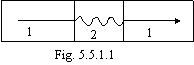The plan of effect is given in a figure 5.5.1.1,
where 1 - superconductor, 2 - segment of normal conductance with a voltage drop
on ends U. The
electron in a superconducting state has not a moment of momentum (is gone
rectilinearly) radius of its trajectory is peer to classic radius of an
electron 2.8·10-13 cm, therefore crystal lattice of a superconductor
for it is practically blank space. Let's term such electron "cold".
When this electron hits on a segment of normal conductance, it gains an angular
momentum from ions of a crystal lattice and its trajectory becomes screw
with radius 2.3·10-8 cm (average speed of heat motion of an electron
at temperature by close to absolute zero about 500 kms/sec). Such electron we
shall term "hot". Though the electrons because of minor mass
practically do not import the contribution to a heat capacity of a solid body,
nevertheless, on a segment of occurrence of "hot" electrons a little
heat should be immersed at the expense of diminution of energy of ions. On a
segment of normal conductance the electron gains energy at the expense of
increase of a forward speed 
. But the same energy it will
gain and at the expense of increase of a tangential velocity on coils of a
screw line. The total increase of energy at a motion in an electric field will
make mV2 =2eU. Hitting again on a segment of
superconductivity the "hot" electron again becomes "cold"
at the expense of losses of an angular momentum on ions of a crystal lattice.
Thus is heat stand out. Besides its exuberant energy or is radiated by a photon
with energy 2eU or is diffused on ions without radiation. At transition
in a superconducting state there is a paradoxical situation: than more
electrical resistance of a conductor, is the more its inhomogeneity, the is
more lighter to an electron to lose an angular momentum and to become
"cold", therefore well conductive metals (argentum etc.) have not
superconductivity. Besides the so-called isotope effect of a superconductivity
is watched: 
, where Tk - critical transition temperature in a
superconducting state, and M - mass of an isotope. With other things
being equal (in samples of isotopes of the same element) it is easier to more
light ions to accept an angular momentum of an electron, than heavy, therefore
formation of "cold" electrons is easier.
As the mechanism of formation of superconducting pairs contradicts bases of a quantum mechanics in a part touched of a constitution of atom, we shall analyze notions of official physics on superconducting pairs little bit more in detail. The superconducting pairs of electrons at superconductivity are stipulated by an exchange of two electrons by phonons (it is quasi-particles - as a matter of fact sound waves). Thus, the official physics separates lattice vibrations from the lattice and this fiction, any more not having physical sense, bonds electrons among themselves. How the sound waves can result in to an attraction of electrons moreover superior a long-range Coulomb repulsion? Why the exchange of phonons gives in an attraction, instead of to repulsion? The total impulse of a superconducting pair is peer to zero point. In pairs the electrons to an opposite impulse are related. How the electrons by means of phonons can be linked, if their velocity of heat motion approximately on two orders exceeds velocity of phonons - speed of sound in metal, and moves they in the counter sides? As the superconducting pairs of electrons become on notions of official physics bosons, all of them can be in an identical ground state. On this the logic a pair of S-electrons in atom too boson, therefore all electrons in atom should pairwise take a ground state that actually does not happen.
The losses by
electrons of an angular momentum are accompanied also by other effects, for
example, by effect Meissner - the superconductor becomes an ideal diamagnetic
and the exterior magnetic field inside it misses. It is bound that the
"cold" electrons ideally follow to a Lenz law and at the expense of
activity of force of the Lorentz moves on a circle, compensating an external
field. The "hot" electrons moves on a screw trajectory also can not completely
to compensate an exterior magnetic field. At losses of an angular momentum the
electrons lose at once seven degrees of freedom from 10 (see chapter
"Birth and death of a photon"), therefore to return them in a normal
state the energy 3.5kTc is indispensable. "Existence of
such slot (power in a superconductor), having at Т 0 breadth about 3.5kTc
(where Tc - the transition temperature in a superconducting
state) gradually shrinking at temperature rise and disappearing at TTc, was set
on sudden change of absorption far infrared (or microwave) radiation in a
superconductor at that moment, when the energy of quantums of this radiation hv
became to equal breadth of a slot". R. Sproul, Modern Physics, М., 1974, page 313.
The exterior
magnetic field instigates acquisition by electrons of an angular momentum at
the expense of force of the Lorentz and at a sufficient intensity field the
superconductivity fades. Apparently, that the energy impart by an external
field should make, for example: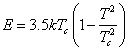 
, that the superconductivity has
vanished. The dependence of a critical exterior magnetic field on temperature
varies the same as also energy E (see, for example, Physics of a
microcosm, М., 1980, page 335 and 347). It
is known, that without an external field the appearance of superconductivity is
not accompanied by heat effect. From a point of view of new physics it is
understandable, since the electrons lost an angular momentum, transmit energy
to a crystal lattice and the system as a whole does not lose and does not gain
energy. The official physics here has problem, since at formation of
superconducting pairs all system as a whole transfers in a more energy
profitable state, that should be accompanied by a heat liberation. At presence
of an exterior magnetic field the heat effect already will and should in
precision correspond to additional energy E.
Here it is necessary to convert the special attention of the reader, that the current in a superconducting ring is watched without changes during a very long time. On a classic electrodynamics charge, uniformly moving on a circle should radiate electromagnetic waves and the current will be promptly stopped. Thus, the classic electrodynamics in a problem of radiation of electromagnetic waves is erroneous. The modern physics, iterating this error, negated the theory of atom of the Bohr also has gone on a way of a bedding of errors against each other.
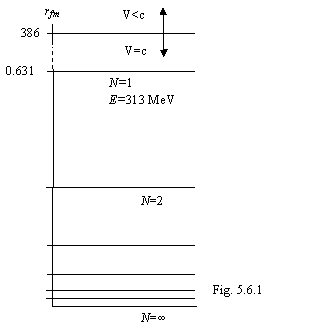
The proton has three particles: the positron and two
photons (or, that is equivalent, two positrons and electron), therefore, for a
proton N=3, since on orbit each particle has an angular momentum . The
constitution of particles will be shown separately. Substituting in (5.4.4)
values of mass of a proton m=938.2723 MeV, we shall discover its radius:
rp = 0.6308 fm. As radius of orbit of components of a proton
was reduced as contrasted to "normal", equal classic radius of an
electron at the expense of gravidynamic interplay in: 2.81794092/0.6308 =
4.46725 times, mass of these components has increased in as much times to
satisfy a law of conservation of angular momentum:
70.025 × 4.46725 = 312.819 MeV (5.6.1),
and mass of a proton as a whole will be 312.819 × 3 = 938.4575 MeV, that means, that inside a proton the minor additional repulsing acts. It is conditioned by that positively charged antineutrino in photons and in a positron look to rotation axis, i.e. spacing interval between positive electric charges it is a little less. Now we can find radiuses of a positron and photon (or electron) inside a proton and, thus to update its constitution under the formulas (5.5.2) and (5.5.3).
Substituting in (5.5.3) r0= 2.81794092 fm, m0= 0.5109991 MeV, m= 312.819 MeV, we shall discover: r= 0.0046032 fm. Thus, radius of a positron or photon in a proton decreases in 612.17 times. In the same ratio the radiuses a neutrino which is formed a positron and a photon decrease. Thus, proton same "empty", as the Universe, galaxy, atom or we with you. At the same time huge the gravidynamic moment of a proton organizes motion of particles around (baryons) in one plane, is similar, how the gravidynamic core will forms a spiral galaxy or rotated star a flat satellite system. The ratio computational to real mass of a proton makes:
mp/m=1.000198, updated radius of a proton: 1.000198×0,6308 = 0.630925 fm.
The characteristics of a proton are shown in table 5.6.1.
Table 5.6.1.
|
Particle |
Angular momentum of a free particle |
Mass of a free particle, MeV |
Mass in a structure of a proton, MeV (N=1) |
Mass at N=2, MeV |
Radius of a free particle, fm |
Radius of a bound particle, fm |
|
Proton |
|
938.2723 |
- |
1876.5446 |
0.630925 |
- |
|
Positron |
|
0.5109991 |
312.819 |
625.638 |
2.81794092 |
0.0046032 |
|
Photon |
|
Depends on energy |
312.819 |
625.638 |
Depends on energy |
0.0046032 |
The energy levels of a proton are shown on a figure 5.6.1.
 |