1. To the reader
2. Actual processes and necessity for new calculuses.
3. Definition of new calculuses similar to differential and integral (D-calculus).
4. D-differential calculus.
5. D-integral calculus.
6. D-differential equations.
7. Examples of applying of new calculuses.
When I studied at school, and after arithmetic make start to teach algebra, our school-ma'am, by not devoting the schoolboys, than is engaged algebra and what for it is necessary, at once has taken the bull by the horns and beginnings on a blackboard to write a+b=c+d and so forth. An impression at first was added up, that the algebra - silly science, but has passed some time, and I have understood, that not algebra, and our school-ma'am is silly. It was necessary at once to explain, that there are some general rules of activity above numerals and then is more convenient to not term 5 apples or simply numeral 5, and under "a" or "b" to understand any numerals or homogeneous objects. In the previous issuing of the book I have assimilated to that silly school-ma'am and at once set up essence of new calculuses, by not finding time to explain, that they by themselves introduce and for what are necessary.
Now differential and integral calculus are unique. It studies, as the change of argument on velocity of that or diverse process influences or, on the contrary, as on an alteration of speed to find change of the function. Many problems from a point of view of a differential calculus are clear to us and easily are decided, for example problem of motion of a body with uniformly increased velocity. Many problems are easy are to translated in comfortable for a differential calculus by a kind many - difficult and this business requires high proficiency, and many - it is impossible. At the same time, frequently there are problems, the physical sense which one is clear to us, but "mathematize" them is rather complex. For example, for us is apparent, that if any microbe in particular time is doubled, after the lapse of this time the total number of microbes will be twice more initial number. In this case we would be helped by calculus as y/y-1=2, where y - current value of a function, y-1 - previous value of a function. Our brains are arranged in such a manner that we can reasonably meditate, comparing current value of some value with its previous value. On it our prognostic abilities here again we are grounded we achieve large successes, even nothing knowing about the reasons of change of a considered function. The tendered calculuses are intended for support of these abilities and operate with current and previous values of any processes. And these values can vary not only in time, but also under activity of any arguments.
2. ACTUAL PROCESSES And NECESSITY For NEW CALCULUSES
Now in practice the rather imperfect technique of the mathematical description any of process will be utilized. Make initial system equations, which one (under the guess of the explorer) more or less adequately reflect actual process. To this system equations set the starting conditions or parameters and then decide by its numerical methods, since the analytical expression frequently cannot be received. The received results compare with practically apparent and in case of considerable variance with the observation data introduce the correctives to initial system equations. Thus the initial system equations fast become complicated (to become simpler it in essence can not) and after several attempts to receive the reasonable solution, forces the explorer to go on the compromise, sacrificing both accuracy and common sense of initial system equations.
Any actual process in any given moment of the development "does not know" neither history, nor future. It develops on the basis of present conditions in this moment which was added up during given process or even up to its beginning. Apparently, that any process at change of conditions of its passing will go with other velocity or even in the other direction, therefore task of the starting conditions is not absolutely correct, since to actual process on them, by and large, not to care a button. Besides the passing and other, indirect processes accompanying explored process will change. The term of "conditions", in which one flow past process is not absolutely successful for the reason, that always of conditions it is possible to find or to number very much, and the given process is influenced only by some of them and in a miscellaneous degree. Therefore there is a sense to enter concept of resource of process. Resource of process is conditions directly influencing to given process, accelerating it or slowing down. At unlimited resource or resource having constant value, it can be not allow, since the course of process in these conditions does not vary. Let's consider some examples.
1. We shall suspect that we study growth of culture of micro-organisms in conditions of unlimited delivery of nutrient materials and removal of products of vital functions. Besides the volume of an incubator also is unrestricted. Apparently, that in this elementary for the analysis a case the external resources of process are unlimited; therefore given process do not influence also them it is possible to not take into consideration. In this case process limits internal resource - velocity of division of cells of micro-organisms. In conditions of a stationary value of temperature it also can be not allow, but at a temperature variation at once there is a temperature resource, which one can be both external, and internal, if the process is accompanied by heat liberation.
2. If in the previous example to limit a volume of an incubator, in a start some time the process will go precisely how in an example 1, but then occurs and starts to influence all stronger resource of restricted space. At the end it will cause to a self-destruction of culture of micro-organisms.
3. At presence of restricted resource of a feed, removal of products of vital functions etc., we shall come besides unfavorable conclusion.
From these examples it is visible, that any process is determined not initially by given regularity and start conditions (apparently, this notion was added up under influence of a mechanics with its stringent determinism), and the resources, which one are disposed by given process in a given instant.
Any process develops on the basis of momentary value of a function, for example, the law of a radioactive decay is received during decay only that each nucleus has particular probability of decay. Nobody will doubt that manages us in any moment to change probability of decay, and just from this moment the process will go in another way. In this sense the tendered below new calculuses have not formal - mathematical, and physical basis, suggesting new value of a function on the basis of its previous value. It enables considerably to perfect mathematical modeling of processes, allowing introducing the correctives to changes of a function on its course, instead of in initial system equations, thus it is possible to not know boundary conditions. Thus, the new calculuses allow as flexibly to operate change of a function, as the external conditions operates change of the most studied process. The mathematical methods sensitively reacting to change of a situation are necessary to applied science as it makes a brain of alive entities. We never shall create artificial reason on the basis of any laws, which one a priori guess a rigid determinism and eliminate any initiative and unpredictable behavior.
3. DEFINITION of NEW CALCULUSES SIMILAR to DIFFERENTIAL And INTEGRAL (D-calculus)
The author hopes, that the enunciated below principles of new calculuses will render the large help to the scientists engaging applied researches, and for the fans of mathematics here immense field of activity.
In a known differential calculus of derivative function:
![]() (3.1)
(3.1)
in a point x term a limit of the ratio of an increment of a function to increment of argument, at aspiration of increment of argument to zero point:
![]() (3.2).
(3.2).
Conditionally we shall term a differential calculus grounded on this definition by a derivative and the relevant integral calculus by d-calculus.
Let's extend definition (3.2), by accepting value ![]() final,
then from (3.2):
final,
then from (3.2):
![]() (3.3).
(3.3).
For further, is more convenient to copy (3.3) as:
![]() (3.4),
(3.4),
whence, allowing (3.1) and by designating ![]() :
:
![]() (3.5).
(3.5).
We go on generalizing, by noting, that at ![]() final,
final, ![]() also
final (for the majority of functions), therefore we shall define set of
derivatives of a function
also
final (for the majority of functions), therefore we shall define set of
derivatives of a function ![]() so:
so:
![]() (3.6).
(3.6).
On the basis of generalized definition of a
derivative of a function (3.6) it is possible to construct set ![]() -calculuses
(we shall term them also differential and integral for the lack of other term).
The d-calculus will be one of particular cases at
-calculuses
(we shall term them also differential and integral for the lack of other term).
The d-calculus will be one of particular cases at ![]() and
and ![]() .
.
I select in set ![]() -calculuses a subset at
-calculuses a subset at ![]() , which
one we shall term as D-calculuses. Thus it is necessary to take into
account, that in actual applied problems for unit it is possible to receive any
change of argument, as units of change of argument in applied problems are
conditional (see examples of practical applied D-исчисления).
, which
one we shall term as D-calculuses. Thus it is necessary to take into
account, that in actual applied problems for unit it is possible to receive any
change of argument, as units of change of argument in applied problems are
conditional (see examples of practical applied D-исчисления).
Thus, the D- derivative of a function ![]() is
determined by us by expression:
is
determined by us by expression:
![]() (3.7),
(3.7),
i.e. it is determined by an arbitrary function from
the subsequent and previous values of a function ![]() , at change of
argument on unit (conditional). From (3.7) we shall discover
, at change of
argument on unit (conditional). From (3.7) we shall discover ![]() :
:
![]() (3.8).
(3.8).
Let's assume: ![]() (3.9),
(3.9),
where U and V - some functions from x.
By substituting (3.9) and (3.8) in (3.7), we shall discover:
![]() (3.10).
(3.10).
We have received main expression for finding of any
derivative from set D, structure which one will be kept and at ![]() .
.
For a composite function ![]() (function from a
function), from (3.10) we shall receive:
(function from a
function), from (3.10) we shall receive:
![]() (3.11).
(3.11).
Let's contact between derivatives of a function ![]() inside D-calculuses.
inside D-calculuses.
For particular calculus ![]() from (3.7) we
shall discover:
from (3.7) we
shall discover:
![]() (3.12).
(3.12).
For calculus ![]() from (3.8) we shall
discover:
from (3.8) we shall
discover:
![]() (3.13).
(3.13).
By substituting (3.13) in (3.12), we shall receive:
![]() (3.14).
(3.14).
The expression (3.14) establishes required connection.
It is interesting also to contact between D-calculuses and known d-calculus.
Let's assume: ![]() (3.15),
whence:
(3.15),
whence: ![]() (3.16).
(3.16).
Let's assume: ![]() (3.17),
whence:
(3.17),
whence: ![]() (3.18).
(3.18).
From equality of the left-hand parts (3.16) and (3.18) we have:
![]() (3.19),
(3.19),
whence it is possible to express ![]() through
through ![]() or on
the contrary. By substituting (3.16) in (3.17) and (3.18) in (3.15), we shall
discover connection between d and D-calculus in an explicit kind:
or on
the contrary. By substituting (3.16) in (3.17) and (3.18) in (3.15), we shall
discover connection between d and D-calculus in an explicit kind:
![]() (3.20),
(3.20),
![]() (3.21).
(3.21).
As the D-derivatives of functions given, for example in points, exist, and d-derivatives is not present, the connection between d and D-calculus for such functions is not uncovered in an explicit kind by expressions (3.20) and (3.21), that is quite natural.
For some (taken as an example) D-calculuses in
the table the rules of differentiation are adduced, which one are received from
(3.10) and (3.11). For an example the elementary functions ![]() are
selected and title of particular D-calculuses
conditionally.
are
selected and title of particular D-calculuses
conditionally.
Table (4.1) of D-derivatives.
Definition of some particular calculuses
|
Kind of D-calculus |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Value of a D- derivative of a function |
|||
|
Type |
|
|
|
|
|
0 |
|
|
|
|
2a |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
Type |
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
Type |
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
Type |
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
Type |
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
Type |
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
Translation
|
|||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
That was more understandable, as the cells of the table are stuffed, we shall consider a particular example of O-differentiation of a function
![]() (4.1),
(4.1),
where U and V some functions from ![]() . Are
apparent, that the previous term of this function will be
. Are
apparent, that the previous term of this function will be
![]() (4.2).
(4.2).
On definition, ![]() (4.3).
(4.3).
On the strength from this definition
![]() ,
,
![]() (4.4).
(4.4).
By substituting (4.1), (4.2) and (4.4) in (4.3), we shall discover value of a O-derivative of a function (4.1):
![]() (4.5),
(4.5),
which one corresponds to value, reduced in table (4.1) (second type of a function, third line).
In the last partition of table (4.1) the formulas of
translation of any of considered D-calculuses in ![]() -calculus
are adduced, which one are directly received from definition of particular D-calculus
and
-calculus
are adduced, which one are directly received from definition of particular D-calculus
and ![]() -calculus, for example:
-calculus, for example:
![]() (4.6),
(4.6),
![]() (4.7),
(4.7),
we exponentiates (4.7) to receive expression for ![]() , which
one we shall substitute in (4.6) and we shall receive the formula of
translation
, which
one we shall substitute in (4.6) and we shall receive the formula of
translation ![]() -calculus in
-calculus in ![]() -calculus:
-calculus:
![]() (4.8).
(4.8).
The formula (4.8) corresponds to the last cell of table (4.1).
Table D- derivatives of elementary functions
is easy for compounding of expression (3.7) or, knowing ![]() -derivative
- from (3.14). For example, the D- derivatives of a function
-derivative
- from (3.14). For example, the D- derivatives of a function ![]() are
those:
are
those: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() etc.
etc.
To differentiate a function it is possible as
directly, and using rules of table (4.1), for example, the function ![]() can be
presented as the ratio of two functions:
can be
presented as the ratio of two functions: ![]() and
and ![]() . In both
cases we shall receive (for O-calculus)
. In both
cases we shall receive (for O-calculus) ![]() .
.
The partial derivatives in any D-calculus are
determined the same as and in d-calculus, for example, if there is a
function several variables ![]() :
:
![]() (4.9),
(4.9),
that the partial derivatives in O-calculus will be such:
![]() ,
, ![]() ,
, ![]() ,
,
i.e. the differentiation on one variable is made at stationary values others variables.
The D-derivatives of the high orders are
received by differentiation of a derivative of the lower order, for example the
![]() -derivatives sequentially of heightened order from a function
-derivatives sequentially of heightened order from a function ![]() will be
such:
will be
such: ![]() ,
, ![]() , ….
, …. ![]()
The D-derivatives of trigonometrical functions
differ from remaining subjects, that unit of change of argument will be a ![]() radian,
for example:
radian,
for example:
![]() (4.10),
(4.10),
then ![]() (4.11).
(4.11).
The O-derivative of a function (4.10) will be:
![]() (4.12),
(4.12),
and ![]() -derivative:
-derivative:
![]() (4.13).
(4.13).
The expression (4.13) is possible to receive and from
(4.12) by taking advantage the formula of translation of O-calculus in ![]() -calculus
from table 4.1.
-calculus
from table 4.1.
The rule of differentiation is universally for any
function - argument of a function by decrease on unit (or on ![]() for
trigonometrical functions) also is noted a ratio between the
for
trigonometrical functions) also is noted a ratio between the ![]() and
and ![]() pursuant
to definition of particular calculus.
pursuant
to definition of particular calculus.
5. D-integral calculus
Primitive a function for a given function ![]() we shall
define similarly, how it is made in d-calculus, i.e. it is such function
we shall
define similarly, how it is made in d-calculus, i.e. it is such function
![]() a D-derivative from which one is peer
a D-derivative from which one is peer ![]() ,
relevant, for example,
,
relevant, for example, ![]() -integral:
-integral:
![]() (5.1).
(5.1).
In a right part (5.1) constant C is present in
![]() -calculus. In other calculuses in a right part the constant can
miss, therefore D-integral can be defined so:
-calculus. In other calculuses in a right part the constant can
miss, therefore D-integral can be defined so:
![]() (5.2),
(5.2),
or, allowing (3.8):
![]() (5.3),
(5.3),
where A - constant factor.
The expression (5.3) is impossible to treat, how a
uncertain D-integral, since, for example, in ![]() -calculus the
constant C in an integrand will vanish, and in a right part remain. For
such calculuses the D-integral will be undefined then, as for example,
the S-integral will be determined, as the constants C and A
in an integrand are saved at differentiation of a primitive.
-calculus the
constant C in an integrand will vanish, and in a right part remain. For
such calculuses the D-integral will be undefined then, as for example,
the S-integral will be determined, as the constants C and A
in an integrand are saved at differentiation of a primitive.
The difficulties of known d-integration are saved and in D-integration, as the D-integral are determined as not constructively, as well as d-integral.
Let's consider anyone uncertain ![]() -integral,
for example:
-integral,
for example:
![]() (4.4)
or
(4.4)
or ![]() (5.5).
(5.5).
We see interesting feature encompassing therein, that
as against set of primitives of a function ![]() in d-calculus
received by parallel carry lengthwise axis y, in
in d-calculus
received by parallel carry lengthwise axis y, in ![]() -calculus
the set of primitives of a given function is received by stretching (squeezing)
lengthwise axis y.
-calculus
the set of primitives of a given function is received by stretching (squeezing)
lengthwise axis y.
The rules of integration for each D-calculus
as are various, as well as rule of differentiation, reflected in table (4.1).
So, for example, the constant factor k is carried out for a sign of a D-integral
![]() so:
so:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, 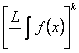 (5.6).
(5.6).
Some indefinite integrals are adduced below. The simplest method of "integration" consists in differentiation of expression, which one is represented to you by useful. The received expression is an integrand, i.e.
![]() (5.7).
(5.7).
1. ![]() is valid at
is valid at ![]()
![]() n
n![]() -
-![]() and also not whole n.,
and also not whole n., ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]() ,
, ![]()
6. ![]()
If the value of an integral in any calculus is known, it is easy for translating in any other calculus, using the formulas of translation of table (4.1). For example, the formula (5.5) with the registration (5.7) and formulas of translation from one calculus in another under table (4.1) can be resulted in an integral № 2 (without a constant factor for simplicity).
The rules of integration are easy for formulating, analyzing rules of differentiation from table (4.1), regarding definition of an integral (5.7).
1. ![]() - or the S-integral of the sum
(difference) is peer to the sum (difference) of integrals of the separate
terms.
- or the S-integral of the sum
(difference) is peer to the sum (difference) of integrals of the separate
terms.
2. O- or the P-integral of product is peer to product of integrals of the separate terms.
3. The L-integral of the sum of the separate terms is peer to product of integrals of these terms.
4. The L-integral of a difference of the separate terms is peer to the ratio of integrals of these terms.
5. The ![]() -integral of product is peer
to product of reverse values of integrals of the separate terms.
-integral of product is peer
to product of reverse values of integrals of the separate terms.
6. Rules of integration for more composite cases, when the function in an exponent of other function is integrated or the function from a function is integrated, directly follow from table (4.1) in which one the type of a function grows out integrations, and the particular D-derivative is an integrand.
Similarly it is possible to enter concept of D-differential equations, and also all what disposes the apparatus modern differential and integral calculus. Certainly, it is a huge transactions, but allowing above-stated, as the business of engineering is spoken, as the principle is clear.
The D-differential equations enter similarly to known d-equations. These equations are contained with unknowns of a function, arguments and derivatives of unknowns of functions (or their differentials) (example 1). The main difference of D-differential equations is that they can be contained derivatives and differentials of any of D-calculuses or even their mixture in one equation (example 1). If the unknowns of functions depend only on one argument, the D-differential equation will be termed ordinary (example 1). If it is some arguments, this equation with partial derivatives (example 2). The order of differential equation terms best of the orders of derivatives or differentials which are included in an equation (example 3). The author considers permissible to relate to D-differential equations as well equations containing integrals (example 4).
Example 1. ![]()
Example 2. ![]()
Example 3. ![]() - second-degree
equation.
- second-degree
equation.
Example 4. ![]()
The methods of the solution of D-differential equations are similar to known methods in d-calculus. The difference is that always it is possible to simplify the solution by selection of the most successful calculus ad-hoc.
Frequently there can be D-differential equations not relating to any of reviewed before D-numerations. In them the connection between current and previous value of a function is rather complex. Let's put examples of integrating of two similar D-differential equations.
Example 5. ![]() , where
R - constant. The integral of this equation is peer:
, where
R - constant. The integral of this equation is peer:
![]() (6.1),
(6.1),
where ![]() - any constant. Really,
from (6.1):
- any constant. Really,
from (6.1):
![]() (6.2),
(6.2),
whence:
![]() (6.3).
(6.3).
The previous value of a function:
![]() (6.4),
(6.4),
whence:
![]() (6.5).
(6.5).
Equating (6.3) and (6.5), we shall discover:
![]() (6.6),
(6.6),
which one coincides with given equation of an example 5.
Verification.
Table 6.1.
|
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
The tabulated data 6.1 correspond to equations (6.1) and (6.6).
Example 6. More composite version of an equation (6.6):
![]() (6.7).
(6.7).
The integral of first item in (6.7) will be peer:
![]() (6.8).
(6.8).
Really, ![]() , whence
, whence ![]() . The integral of an augend in (6.7) will
be peer:
. The integral of an augend in (6.7) will
be peer:
![]() (6.9).
(6.9).
Really,  , whence
, whence
![]() . Putting together (6.8) and (6.9), finally
we shall discover:
. Putting together (6.8) and (6.9), finally
we shall discover:
![]() (6.10).
(6.10).
From reduced examples it is visible, that any ratio in an obvious or implicit kind linking two values of a function concern to D-differential equations. At forecasting we as a matter of fact always search for the solution of a D-differential equation.
7. EXAMPLES of APPLYING of NEW CALCULUSES
Let's consider some examples of practical use D-исчислений.
Problem about a radioactive decay.
It is known, that mass M of radioactive matter
decreases twice in period ![]() - time of a half-decay,
i.e.:
- time of a half-decay,
i.e.:
![]() (7.1)
or
(7.1)
or ![]() (7.2).
(7.2).
Integrating (7.2), we shall receive:
![]() (7.3).
(7.3).
For unit of a time scale we picked ![]() . To
receive relation from
. To
receive relation from ![]() , it is necessary
, it is necessary ![]() to
result in a selected scale, i.e.:
to
result in a selected scale, i.e.:
![]() (7.4).
(7.4).
By substituting (7.4) in (7.3), we shall receive:
![]() (7.5).
(7.5).
At ![]()
![]() , therefore, we shall
finally have:
, therefore, we shall
finally have:
![]() (7.6),
(7.6),
As is an equation of a radioactive decay.
Let's consider one more problem resulting in to a ![]() -differential
equation. Let's suspect that we close down a certain surface by layers of the
opaque chaotically arranged particles with mark-to-space ratio
-differential
equation. Let's suspect that we close down a certain surface by layers of the
opaque chaotically arranged particles with mark-to-space ratio ![]() in each layer. It is
required to find a closed area y, as a function of number of layers x.
Is apparent, that:
in each layer. It is
required to find a closed area y, as a function of number of layers x.
Is apparent, that:
![]() (7.7).
(7.7).
Whence it is easy to find a ![]() -differential
equation, by transferring
-differential
equation, by transferring ![]() in the left-hand part
(7.7):
in the left-hand part
(7.7):
![]() (7.8).
(7.8).
Integrating (7.8), we shall receive:
![]() (7.9).
(7.9).
Let's check up (7.9), ![]() -differentiate:
-differentiate:
![]() (7.10)
(7.10)
![]() (7.11),
(7.11),
![]() (7.12).
(7.12).
By dividing both parts (7.12) on ![]() , we
shall receive:
, we
shall receive:
![]() (7.13).
(7.13).
From (7.11): ![]() (7.14)
(7.14)
By substituting (7.14) in (7.13), we shall discover: ![]() , i.e.
(7.8).
, i.e.
(7.8).
Let's look, as in ![]() -calculus the
problem of definition of a kind of a function will look, the second differences
by which one are constant. As is known it is parabola. Apparently, that second
the
-calculus the
problem of definition of a kind of a function will look, the second differences
by which one are constant. As is known it is parabola. Apparently, that second
the ![]() -derivative thus is constant:
-derivative thus is constant:
![]() (7.15).
(7.15).
Integrates (7.15) once:
![]() (7.16).
(7.16).
Integrates (7.16) once again:
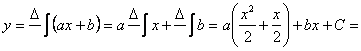
![]() (7.17).
(7.17).
Let's check up (7.17):
![]() (7.18).
(7.18).
![]() (7.19),
(7.19), ![]() (7.20).
(7.20).