3

3. AUDIT of a QUANTUM MECHANICS

In this chapter we shall analyze fundamentals of a modern quantum mechanics. It as a matter of fact not corpuscular and wave. Will be shown, that though it and operates with mass and energy of a particle, as a matter of fact properties of particles in it are skipped in a favour to wave properties. In this case it is easy to receive quantum system conditions, stands only legally or clandestinely to present a particle as a standing wave. Thus find explanation some experimental facts which are not explained by classic mechanics. Simultaneously there are outcomes, not having physical sense. For example, any bound particle in a wave quantum mechanics appears disjointed on separate slices and spread on space, since a particle is not present there, where the wave function is peer to zero point (in nodes of a standing wave) and is spread in space, where the wave function is different from zero point (in antinodes of a standing wave). Particle, bound with a standing wave, too is immobile, though can be in a force field and should move. But then the standing wave is transformed into a traveling wave and quantumness of levels of energy at once disappears. Besides constant originating of perpetuities at calculations, from which one it is necessary by hook or by crook to liquidate, literally martyrs a wave quantum mechanics.

New physics connects wave properties of particles to motion them on a screw line. A reason of such trajectory is the originating of a gravidynamic field at motion of gravitational charges. On the basis of it is possible to call new physics as a corpuscular quantum mechanics as against an official wave quantum mechanics. Thus, now in our disposal will be a wave quantum mechanics, classic mechanics and corpuscular quantum mechanics. Further we compare these three approaches in the indicated sequence to physical phenomena and we shall see, with what of them not conflicts with sensible physical sense.

Comments of the author to chapter 3:

1. Classic and quantum physics.

The familiarization with properties of a microcosmos has provoked large doubts in applicability of the laws of classic physics, quantum physics as a result of which has appeared. The scientists, nostalgic till now on «clean» classic physics are easy are to understood - with replacement necessarian of the description of a world by the probabilistic description causes the internal protest against «divine heaven». But also they should understand, that classic physics irrevocably has sink into oblivion and any attempts to reanimate it in a primitive kind are useless. An alone path to return in physics common sense - considerably «to correct» classic physics, essentially, to elaborate neoclassic physics grounded on a principle of determinism, tested by centuries.

The quantum physics is founded on the probabilistic description of a world. We, certainly, can use a law of probability for statistical of the description of composite events, but to forecast, for example, what party the thrown coin will fall by it is impossible to forecast with probability more than 0.5. Now we shall throw this coin and with probability to equal unit it will fall by that party, which one we see after a throw. Thus, after the event has taken place,its probability is peer to unit. Therefore all our speculations and calculations before event are fiction. The same fiction is also probabilistic description of a world, i.e. quantum wave physics is mock-science, causing us in fallacy. At any moment of time any particle of a microcosmos is in a strictly definite place and has definite speed. That there is with it through instant official physics in accuracy does not know, and its probabilistic suppositions nothing cost, since with probability to equal unit will not coincide that will happen through this instant.

2. The quantum mechanics does not have foundation.

The creators of a quantum mechanics supposed, that its foundation can be served with formation of a standing wave in microsystems, bound with wave properties of particles. Then the integer values of quantum system conditions are easily explained, but here there is a principled difficulty, which one does not allow to realise this idea. I shall remind indispensable conditions of originating of a standing wave. The standing waves are a particular case of an interference as a result of superposition of two waves distributed in opposite directions with identical frequency, polarization (for shear waves) and identical amplitude in applicable coordinate. In a standing wave there is absent a carry of energy, since a straight and backward wave transfer energy in equal quantities. At violation of any of listed conditions the formation of a standing wave is impossible. Nevertheless, official physics applies a Schrodinger equation in all cases, when the formation of a standing wave is impossible. As in substantial microsystems anywhere there are no vertical walls of a potential well, the reflected wave can not be diffused in a direction dropping. For example, in atom the spherically symmetric electrostatic field of a nucleus has not anywhere not vertical «walls», by consideration of «tunnel» effect the reflected wave can not have amplitude dropping, therefore formation of a standing wave is impossible. This principled difficulty of a quantum mechanics its creators is fine understood, therefore considered the extremely invented unreal model systems with vertical walls of a potential well, and the conclusions of such consideration suffered on real systems. It is a not scientific method of investigations. What for creators of a quantum mechanics (which one are considered as the great scientists) neglected scientific bona fides for the good of achievement of the purpose? The answer is not present. There is an alone suspicion, that the mankind periodically is struck by a global stupefaction on unknowns to reasons (almost simultaneously with a quantum mechanics there were two world wars, revolution, civil war and relativity theory).

3.1. Motion of a free particle and indeterminacy relations of the Heisenberg

Wave quantum mechanics. Uncertainty of the Heisenberg:

P_xxh (3.1.1)

is possible for considered one-dimensional problem to copy as:

Pxh (3.1.2).

If we precisely find out value of a impulse of a particle (P=0), pursuant to (3.1.2) x= and the particle with equal probability is in any place of an infinite axis x. Though probability to meet a particle on all infinite axis x is peer to 1 (particle is, but it spread on all axis) the probability to meet it in any point x_i is peer to zero point (1/=0), i.e. in any point of an axis of a particle is not present. This irresolvable within the framework of common sense an inconsistency. If to take into account, that in a considered case a projection of a impulse to an axis y and the axis z is peer to zero point, and P_y and P_z also are peer to zero point and then the particle is spread on all infinite space.

As a matter of fact, the indeterminacy relations of the Heisenberg prohibit any interplay of microparticles. Let's consider, for example, collision of particles in colliding beams. Apparently, that the collision of two particles takes place in a definite point of space, but then impulses (and the energy) these particles indefinitely large and was not of sense them to accelerate. If “collides” two particles with definite impulses, the probability of their meeting is peer to zero point, since they with equal probability can be found in all infinite space. Same concerns and to an exchange interaction by means of virtual particles. Thus, the ratio of the Heisenberg, explaining originating of virtual particles, simultaneously deprive their aptitude somehow to exhibit themselves, that is possible only through interplays.

The indeterminacy relations of the Heisenberg contradict a relativity theory, that is confirmed by the following quotation (Physical encyclopedia under edition A.M. Prohorov, т.3, M, 1992, page 494): «The main concept of a relativity theory - the event, under which one is understood something occurring in the given instant in the given point of space (for example, light flash or concurrence of a finger of a device with a point). The substantial events have a final expansion in space and time, therefore concept of event of a relativity theory is idealization. The experiment demonstrates, that the applicability of this idealization is very high, down to spacing intervals ~10^-16 cm and times ~10^-26 sec». Apparently, that the same experiment disclaims indeterminacy relations.

Classic mechanics. Here contradictions do not arise. Knowing initial velocity and traffic route, we can precisely calculate a trajectory of motion of a particle and always we shall point, when and where it to meet.

Corpuscular quantum mechanics. The physical sense of uncertainty of the Heisenberg was uncovered in the previous chapter. If we precisely know a projection of a impulse of a particle to an axis x, along which one it is gone (figure 3.1.1), uncertainty of a position of the particle:

(3.1.3)

is peer to a wavelength de Broglie or circumference of cross section of a screw trajectory.

Tangential and forward speed of a particle on a screw trajectory are peer, therefore projection of a impulse to traffic route is always constant and is peer:

(3.1.4).

On the other hand, angular momentum of a particle:

(3.1.5).

Allowing, that and substituting (3.1.3) and (3.1.4) in (3.1.5), we shall discover:

(3.1.6).

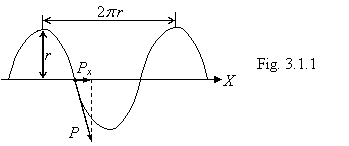Apparently, to be saved of uncertainty in a position of a particle in space, it is necessary to point not only initial velocity and traffic route, but also initial phase of motion, i.e. initial position of a particle on screw trajectory. Further, as well as in classic mechanics, we can calculate a trajectory of particle motion and with probability to equal 1 to meet it in any desirable point of this trajectory.

Comments of the author to chapter 3.1.

Examples of inconsistencies with indeterminacy principles:

1. Atom of hydrogen.

The atom of hydrogen is stable, therefore for any period t the change of energy of this atom is equal to zero point, therefore Et=0. Radius of atom of hydrogen is peer to radius of Bohr orbit, therefore x=r=0. The impulse of electron on orbit of Bohr does not vary P=mV=0, therefore Px=0. The supporters of speed - vector this indeterminacy can esteem after each full revolution.

2. Ionization of atoms.

Let's take advantage of an indeterminacy principle by the way Pxh/2 (1) in application to any electron of atom, where P=P - impulse of an electron, and x=r₀ - classic radius of an electron. Energy of an electron E=P²/m_e (2) where m_e - electronic mass. From (1): P²=(h/2 r₀)² (3). By substituting (3) in (2) and tabulared values of constants, we shall find, that the indeterminacy relations urge any electron of atom to have energy 96 Мэв. Apparently, that this energy exceeds an ionization energy of inner-shell electrons even of high-gravity atoms, therefore any atoms instantaneously will lose all electrons, by keeping bare nuclei. The orthodoxes here fall in an inconvenient situation and to get out, will accuse the writer of application of the insecure size of an electron (from their point of view). But that the outside electrons were not lost by atom, their size should be in some thousand times more, that is incredible. The official notions outgo from the dot size of an electron or Planck size. Then the energy of electrons will be received in general killing. By the way, the indeterminacy relations cross all gamble of the string theories, since the sizes of «strings» guess to equal Planck length 10^-33 cm. In this case energy of «strings» in 10⁴⁰ times should exceed energy of electrons. Full delirium!

3. The indeterminacy relations lead to an irresolvable antagonisms.

Let's record two known expressions of an indeterminacy relation:

Eth/2 (1) and Pxh/2 (2). The left-hand parts (1) and (2) fall into to the same expression, therefore, are peer among themselves. Let's equate: Et=Px (3). Is convertible (3): E/P=x/t (4). Let's decrypt values of physical values in (4): E=mc² - change of a total energy of a particle, P=mV - change of impulse of a particle, x/t=V - alteration of speed of a particle. Let's substitute all in (4): mc²/mV=V or c=V. Thus, the joint solution of indeterminacy principles gives apparent silly outcome: all microparticles in any conditions of a quantum mechanics should move with speed of light. This outcome contradicts orthodox notions of a relativity theory and test datas, as the speed of a microparticle can be somehow small. From here we make a conclusion, that a quantum mechanics - false theory in the most fundamentals.

4. Latent mathematical error in indeterminacy principles.

Let's record an indeterminacy principle by the way: Px=h/2 (1). Let's calculate P=P₂-P₁= h/2 (1/x₂-1/x₁)= h/2 (-x/x₂x₁) (2). Whence: h/2 = -Px₂x₁/x (3). Comparing (3) and (1) it is possible to make conclusions: 1. The left-hand part of equality (1) is always negative, and dextral positive, that is impossible. 2. Equating (1) and (3), we shall find: x= i (x₂x₁)^(1/2), i.e. x - always imaginary number not having of physical sense, therefore have not sense and indeterminacy principle, as the similar procedures with a correlation Et=h/2 result to precisely to the same outcomes.

3.2. Motion of a particle at the bottom potential wells with flat bottom

Wave quantum mechanics. For the solution of this problem will use a steady-state Schrodinger equation. Thus is enabled, that the potential energy does not depend on time (stationary motion). Here it is necessary a little words to tell about the Schrodinger equation. To construct huge section of science, such, as a wave quantum mechanics, on the basis of only one equation - risky occupation. Always it is possible to show, that any equation of physics or is erratic or the limits of its applying are limited, it is not exact, means too is erratic. The "ideal" equations do not exist, therefore we are compelled to idealize nature, devising "ideal gas", "point charges", "free bodies" etc. Behind any equation the definite physical notions and postulates are stands. A validity of a Schrodinger equation confirm by concurrence of its some solutions with the experimental data. Apparently, that such concurrence confirms applicability, however does not demonstrate regularity. The same outcome frequently can be received from opposite notions. And if at the solution of an equation the "necessary" outcomes coincide and are rejected "not necessary", in the total always it is possible to receive that is necessary.

For example, if kinetic energy of a particle:

(3.2.1)

to express through a impulse of a particle, it is necessary to record:

(3.2.2).

In Schrodinger equation expression (3.2.2) after multiplying numerator and denominator on m record as:

(3.2.3).

Thus distort physical sense of kinetic energy on opposite. As for a free particle P=const, E_k on (3.2.3) is inversely proportional to a particle mass. For what it is done? To not busy oneself with a taking the root from the sum of squares of projections of an impulse:

(3.2.4),

the necessity for physical explanation of two values of the root passes. If to use (3.2.2), the speed of a particle is a principled handicap, since in a standing wave "particle" is immobile.

The stationary motion is possible only in two cases.

1. On a circular orbit. For this case the steady-state Schrodinger equation does not approach, since it leave outs bond energy, which one is the sum kinetic and potential energy. To receive a total energy, which one is constant, it is necessary to take into account and bond energy. Invariable there is only algebraic sum kinetic, potential and bond energy.

2. In a potential well with flat bottom. In this case particle is free and can change a traffic route, only being mirrored from walls of a well. Thus the kinetic energy of a particle does not vary and coincides a total energy of a particle, since the potential energy in a considered problem can be equated to zero point.

At the solution receive, that for walls of a well the wave function receives zero values. Physically it means, that "stick" to a particle the wave, inside a well is esteemed only with standing waves, i.e. on length of a well the integer of half-waves should be stacked. Therefore are received only quite defined values of kinetic energy, which one can have the wave - particle. Here at once there are two problems, the wave quantum mechanics does not respond on which one.

1. Whence agent of an external action (photon, atom or diverse particle) can know about "allowed" energy levels to change kinetic energy of a particle in a well on definite value. If the transferred impulse will not correspond to a level of energy, the formation of a standing wave will become impossible and all levels at once will disappear.

2. Why the standing waves are taken into consideration only, and the general case of a traveling wave is skipped? Naturally, that at the registration of traveling waves all conclusions about quantizing energy in a potential well will appear error.

The standing waves are a particular case of an interference as a result of superposition of two waves distributed in opposite directions with identical frequency, polarization (for transverse waves) and identical amplitude in applicable coordinate. In a standing wave there is absent a carry of energy, since a straight and backward wave transfer energy in equal quantities. At violation of any of listed conditions formation of a standing wave impossible.

In this connection there are additional problems.

1. What mechanism of an interference of a particle with itself?

2. How one particle is partitioned on some parts, its each part is in antinodes of a standing wave and misses in nodes?

Here there is no sense to adduce the solution of a Schrodinger equation for each specific target to not puzzle to the reader. Wishing to travel in composite mathematical mazes of the solutions can address to the special literature. I shall adduce finished outcome (for example, G.E. Pustovalov. Atomic and nuclear physics. The Moscow university, 1968, page 51):

(3.2.5),

where l - length of a potential well.

Classic mechanics. The physical sense, furbished of quantum mechanical heapings, of a problem about a particle in a potential well can be illustrated by only classic model. Let's take a cord of mass m, fixed on ends and we shall begin to excite in it transverse vibrations so that the standing wave, for example, from one half-wave was formed. Apparently, that for this purpose it is required to expend definite energy. To organize a standing wave from two half-waves, it is necessary to add a portion of energy not what has got, and definite value. As a result of consideration of this classic model, we shall receive precisely same outcomes, as well as at the solution of a Schrodinger equation. Therefore "marvelous" originating of quantum levels of energy at motion of a particle in restricted area is a fraud - outcome of the quantum makeweights of energy for ensure of formation of a standing wave.

Corpuscular quantum mechanics. Here it is necessary to consider completely absurd from the point of view of physical sense model, when the particle, being mirrored from walls of a well, will form "standing wave" (figure 3.2.1). But this situation is not more absurd, than particle, sliced on slices, fixed with the uniformly distributed slices on bottom of a potential well.

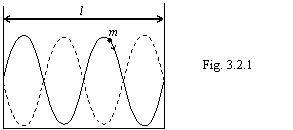The right-handed particle, moving along a well, is mirrored from a wall and is gone backwards already as a left-handed particle. Let's proclaim the absurd requirement, that inside a potential well always there was "standing wave", i.e. on length of a well the compliant particle stacked an integer of half-coils of the screw trajectory. Apparently, that the minimum energy of a particle will in the event that in a well is stacked only of half-coil of a screw trajectory. At some more smaller energy a wavelength de Broglie (the step of a screw trajectory) becomes such, that the half-wave are not stacked any more in the sizes of a well and the formation of "standing wave" is impossible. Concerning it official physics speculates around "of zero oscillations", virtual particles of vacuum and other rubbish.

Момент импульса частицы на витках винтовой траектории:

(3.2.6).

The wavelength de Broglie is peer to a circumference of cross section of a screw trajectory:

(3.2.7).

Substituting (3.2.6) and (3.2.7) in (3.2.1), we shall discover:

(3.2.8).

Condition of "standing wave":

(3.2.9),

where n - an integer (n=1,2,3…), we shall substitute in (3.2.8) and we shall receive (3.2.5). Thus, we have received full concurrence with official quantum mechanical calculation. Thus we did not use at all Schrodinger equation. Nay, thus the primitive mathematical apparatus eliminating a capability of disputing of obtained outcome is utilized (compare to official manipulations at a conclusion (3.2.5), by addressing to the indicated literature). As neither official solution of this problem, nor example of the solution tendered new physics, have not physical sense, alone conclusion, which one can be made is a doubt in a regularity of a Schrodinger equation.

3.3. Motion of a particle in a potential well with energy loss

Wave quantum mechanics. For the indicated problem the steady-state equation of the Schrodinger does not approach. The potential energy of a particle permanently varies in time, and the solution of a common Schrodinger equation is so complex, that it is make no sense with them to take trouble, when it is possible simply to receive levels of energy for this problem with the help of a classic or corpuscular quantum mechanics without usage of a wave quantum mechanics.

Classic mechanics. On a figure 3.3.1 the potential well as the barrel by an altitude h₀ with flat bottom is shown.

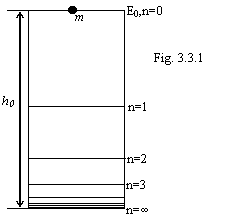Let's take a bead of mass m and we shall release it from an altitude h₀ without initial velocity. If the energy losses miss, the bead will be indefinitely to jump, each time returning in initial point. In this case total energy of a bead remains always numerically equal E₀, passing from potential in kinetic and back. Apparently, to reach bottom of a potential well, the bead should lose energy:

(3.3.1),

where g - acceleration of gravity.

Let's suspect that at each shock about bottom of the barrel the bead will lose a definite fraction K from initial energy. Then:

(3.3.2).

At i-th recoil:

(3.3.3),

where n=0,1,2,3,… - number of recoils. From (3.3.3) it is visible, that at K=0 (the ideal elastic bead and barrel), the bead will jump eternally, and at K=1 (a plasticine bead) it will adhere to bottom of the barrel and E₀ at once will turn to heat. At K=0.5 levels of energy are figured on a figure 3.3.1.

We see that the number of energy levels is indefinite, and they are inspissated near to a ground state. This picture completely corresponds to atom of hydrogen of new physics and directly is opposite to orthodox notions. The total energy of a bead this problem is peer to zero point and is the algebraic sum potential, kinetic energy and bond energy: Е_tot=Е_pot+Е_kin+Е_tie=0. All energy levels of official physics are arranged "heels over head" because of misunderstanding of a difference between energy of a level and bond energy. For our problem:

(3.3.4).

The formula for energy levels of atom of hydrogen under the theory of the Bohr, wave mechanics and corpuscular mechanics has the same kind:

(3.3.5),

where E_i - energy of a level, which one is lay off from a ground state, E₀ - greatest possible energy of a level. Apparently, that electron-binding energy with a nucleus:

(3.3.6).

At n, E_tieE₀.

Corpuscular quantum mechanics. Here reasoning same, as well as in the previous point. Only instead of a bead the electron with initial potential energy E₀ is considered. Energy after the first recoil from bottom of a potential well will be:

(3.3.7),

and after i-th recoil:

(3.3.8).

In the theory of atom of new physics and in the theory of formation of a solar System is shown, that the radial velocity of a body in a new quantum condition in an integer of time is less than initial velocity:

(3.3.9).

By substituting (3.3.9) in (3.3.8), after some transformations we shall receive:

(3.3.10).

By substituting (3.3.10) in (3.3.8), we shall discover:

(3.3.11).

Energy of connection of an electron will be:

(3.3.12).

At each recoil from bottom of a potential well the electron beams photons at the expense of a Bremsstrahlung.

3.4. Tunnel effect

Wave quantum mechanics. By consideration of a tunnel effect official physics is compelled to enable a reflection coefficient from a wall of a potential well (potential barrier) less unit, that the particle could penetrate inside of a barrier. Thus a main condition of formation of a standing wave at once is upset, and the quantum levels fade, being transformed in an continuous spectrum. Thus there is a following dilemma. If we want to keep quantization, we should refuse a tunnel effect, and if we want to keep a tunnel effect - it is necessary to refuse a set of quantum levels of energy. For further it is necessary to be feigning nothing intelligent about this inconsistency.

For the solution of this problem will use also steady-state equation of Schrodinger, though it is necessary to use a time equation. Thus we shall deal with a traveling wave, since the standing wave has not property to penetrate into any encumbrances. By consideration of a tunnel effect enter a permeability coefficient of a barrier:

(3.4.1),

where N - number of particles elapsed through a barrier, N₀ - number of particles dropping on a barrier. As the Schrodinger equations does not give any indications on difference of particles from each other, that, apparently, that if one particle was mirrored from a barrier, all remaining particles will be mirrored also. If the particle has passed through a barrier, will penetrate also all remaining. To leave from this ado, it is necessary each particle, dropping on a barrier, to introduce by a wave, instead of particle. Only wave is capable partially to be mirrored from a barrier, partially to penetrate into a barrier, partially to be occluded in it and to come out on other side of a barrier. In outcome we receive an improbable condition for a particle. The part it is mirrored, the part is occluded in a barrier, and the part passes through a barrier. Therefore official physics by manipulations which are not having of physical sense, receives the formula for a permeability coefficient of a potential barrier also dispossessed of physical sense (see, for example, G.E. Pustovalov. Atomic and nuclear physics. The Moscow University, 1968, page 58):

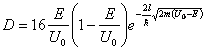(3.4.2),

where E - the common energy of a particle of mass m, passing through a potential barrier, width l for overcoming which one is indispensable energy U₀. It is supposed, that E<U₀ and the classic particle will not overcome a barrier. But, by putting E=U₀ (the classic particle will overcome a barrier), from (3.4.2) it is visible, that thus of D=0, i.e. the "quantum" particle is not capable to overcome a barrier. If E>U₀, (3.4.2) gives such outcome, which one cannot give reasonable physical sense. D becomes negative, and in an exponent there is an imaginary value. The orthodoxes prefer to hide this nonsense, by designating:

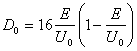(3.4.3)

and considering D₀1. In fine of this fraud receive quite modest expression:

(3.4.4).

Classic mechanics. For overcoming a barrier by a "classic" way official physics attracts an indeterminacy principle of the Heisenberg, on which one it is impossible simultaneously precisely to define kinetic and potential energy of a particle. Therefore missing potential energy official physics "borrows" among kinetic energy to not upset a fundamental energy conservation law. Apparently, that without engaging additional energy the tunnel effect is impossible, since it would contradict an energy conservation law. Therefore, if the classic particle has not enough a little energy, it can be “added”. For example, if the kinetic energy of a bowled bead is less than that potential energy, which one it is necessary to impart to overcome a barrier, it is necessary to take into account that except for moving with definite speed the bead also is gyrated at rolling therefore its full energy is more kinetic. To microparticles they are easier - always can receive additional energy from vigorous particles of "tail" boltzmann of distribution.

Corpuscular quantum mechanics. Here we shall was clandestinely pull idea that except for translational kinetic energy the particle has the same energy and on coils of a screw trajectory, since its translational and tangential speed are peer. Legally this idea will be formulated at arguing -decay of atomic nuclei. Let's consider a figure 3.4.1 on which one the potential barrier and trajectory of motion of a particle near to top of a barrier is figured.

The factor of "permeability" of a barrier will be determined by the formula (3.4.1). If on a barrier the set of particles with a miscellaneous phase of motion drops, the number of dropping particles is proportional to a circumference of cross section of a screw trajectory (wavelength de Broglie):

(3.4.5),

and the number of particles elapsed through a barrier is proportional to a part of an arc of a screw trajectory, prominent above a barrier:

(3.4.6),

where - central angle of an arcs expressed in radians. By substituting (3.4.5) and (3.4.6) in (3.4.1), we shall receive:

(3.4.7).

The boom h prominent above a potential well of a segment is determined by known expression (see, for example, I.N. Bronstein, K.A. Semendiaev. The reference book on mathematics. М., 1962, page 169):

(3.4.8).

Let's discover from this expression :

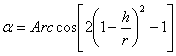(3.4.9).

By substituting (3.4.9) in (3.4.7), we shall receive:

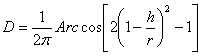(3.4.10).

Apparently, that the connection between and energies is established by a following ratio:

(3.4.11).

Really, if h=2r (U₀=0), all particles will pass through a barrier. If h=r (U₀=E), half of particles will pass, and half will be mirrored from a barrier. If h=0 (U₀=2E), any particle through barrier to pass can not. By substituting (3.4.11) in (3.4.10), we shall discover finally:

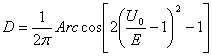(3.4.12).

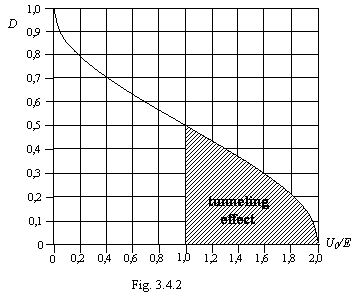
The graph of change D depending on relation U₀/E is shown on a figure 3.4.2.

Thus, we have explained "tunneling" effect within the framework of new physics. It appears that the particle can overcome a potential barrier an altitude which one is almost peer to double energy of translational motion of a particle. At equaling of energy of a particle and the altitude of a barrier, it overcomes 50 % of particles, remaining are mirrored. If the speech goes about one particle, 50 % of impacts of a particle with a barrier will cause to its reflection, and 50 % will cause to passing through a barrier. It is fair, since new physics negates formation of a standing wave up to a barrier, therefore at each rapprochement of a particle with a barrier, its phase of motion on a screw line will be miscellaneous. Even at an altitude of a barrier only 10 % from energy of a particle, almost 15 % of particles are mirrored from it.

On the basis of the obtained outcomes of this section and section 2.1.2 it is possible to formulate a following apparent rule: the more difference in quantity of sensible physical sense of initial notions, the stronger obtained outcomes differ.

3.5. Linear harmonic oscillator

Wave quantum mechanics. In this problem official physics again cuts up an oscillator on separate chunks in quantity n, arranged on line of oscillations. In nodes of a standing wave of an oscillator the probability density of a particle presence is peer to zero point. Final expression for levels of energy of an oscillator (see, for example, R. Sproul. A modern physics. "Science", М., 1974, page 164):

(3.5.1),

where n=0,1,2,3…, ₀ - oscillation frequency of an oscillator in a ground state, i.e. the oscillator can be only on higher energy levels concerning a ground state. At n the oscillator should receive indefinitely large energy that is dispossessed of physical sense. The minimum energy of an oscillator on official notions makes h₀/2.

Classic mechanics. The radiation of a dipole is enough well worked in classic physics. The dipole beams in a direction to perpendicular motion of a charge and in the event that on ends of a dipole of opposite phases of oscillations. At identical phases of radiation is not present.

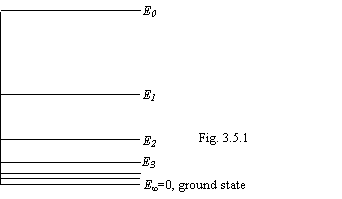Other classic model of an oscillator can be served with a pendulum. If it does not lose energy (not "beams"), then rocks eternally. If with each swinging will lose a portion of energy some fraction from initial energy, its energy levels will lie pursuant to a figure 3.5.1. During quantum energy loss the oscillation frequency of a pendulum does not vary, oscillation amplitude decreases, and the lost portions of energy step-by-step decrease.

Corpuscular quantum mechanics. At a harmonic oscillation of a charged particle:

(3.5.2)

its speed:

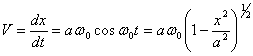(3.5.3).

At x=0:

V=V_max= (3.5.4),

where - amplitude, - cyclical frequency. In this case oscillator has only kinetic energy. At x= V=0 and the oscillator has only potential energy. The total energy of an oscillator numerically will be peer:

(3.5.5).

(3.5.4) we shall substitute in (3.5.5):

(3.5.6).

Angular momentum of an electron:

(3.5.7)

let's substitute in (3.5.6):

(3.5.8).

The motion of an oscillator is shown on a figure 3.5.2.

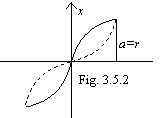From a figure it is visible, that the amplitude of an oscillator oscillation is peer to radius of a screw line. In view of it, and allowing, that , and , the expression (3.5.8) start a kind:

(3.5.9).

At radiation of an oscillator V_max can decrease only in an integer of time:

(3.5.10),

where n=1,2,3… (3.5.10) we shall substitute in (3.5.6):

(3.5.11).

From (3.5.11) it is visible, that at n=1 oscillator will have maximum energy , and at n the oscillator loses all energy and does not beam any more (is in a ground state). This fact can be interpreted doubly. Or the electron is immobile, or is gone on circumferential, instead of elliptical orbit, therefore does not beam. In the latter case there is a sense E_i to use for calculus of electron-binding energy with a nucleus:

(3.5.12).

At n maximum bond energy (ground state without radiation):

(3.5.13).

Energy of an oscillator h₀/2 orthodoxes consider as minimum energy "of zero oscillations" (see expression 3.5.1). New physics adheres to opposite judgement, h₀/2 - greatest possible energy of an oscillator. Really, for atom of hydrogen on orbit of the Bohr (ground state):

(3.5.14),

where r₀ - radius of the Bohr orbit. Let's take into account still known ratio: , , and all we shall substitute in (3.5.13):

(3.5.15).

Substituting in (3.5.15) tabular data, we shall discover:

=2,1795×10^-11 ergs = 13,60 eV (3.5.16),

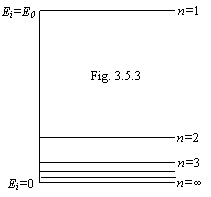that indicates a regularity of notions of a corpuscular quantum mechanics and inaccuracy of a wave quantum mechanics. The levels of energy on (3.5.11) are shown on a figure 3.5.3.

Comparing the formulas (3.5.1) and (3.5.11) we see, that the power spectrum of an oscillator in a wave quantum mechanics is limited on the side of low energies (n=0), but is not limited on the side of high energies (resolves so-called "ultra-violet catastrophe"). The power spectrum of an oscillator in a corpuscular quantum mechanics, on the contrary, is not limited on the side of low energies (n=), but is limited to value h₀/2 on the side of high energies. It completely corresponds to experimentally studied power spectrums of different processes, which one are sharply limited by some maximum value of energy.