22. THE REASONS of QUANTUM CONDITIONS of SPACE BODIES

The satellite system can be formed around of a central body at capture of space bodies only with a certain wavelength. Therefore for macrobodies it is necessary to distinguish "wavelength" macrobody, which one depends on a progressive speed on coils of a screw trajectory and "wave amplitude", which one depends on a tangential velocity of macrobody on coils of a screw trajectory. At the same translational velocity V_f (identical "to a wavelength"), the tangential velocity V_t should be determined by a ratio:

V_t=V_f∙n                                                  (22.1),

where n - integer 1. Only under condition of (22.1) during passage of "wavelength" the body will have time to make precisely one revolution on an coil of a screw trajectory. It is well visible from a figure 22.1, where the trajectories of motion of space bodies’ lengthwise axis O-O are to scale figured.

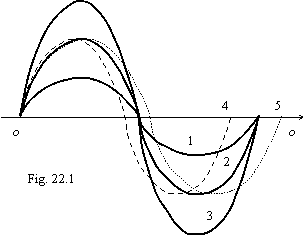
The solid line shown trajectories of bodies with one wavelength, but with miscellaneous amplitude relevant to a quantum condition, accordingly, 1, 2 and 3. Radius of a screw trajectory of these bodies is proportional to a square of a quantum number. The dashed line rotins a trajectory of a body, which one for same time has time to make more than one revolution around of an axis O-O, i.e. possessing a smaller wavelength. The dot line has shown a trajectory of a body, which one for same time has no time to make a revolution around of an axis O-O, i.e. possessing the greater wavelength.

In the chapter "Theory of gravidynamic interaction" we have found the formula of a wavelength for macrobodies under the form conterminous with a de Broglie formula:

R=S/mV                                                (22.2).

This formula is valid at equal translational and tangential velocity. In a macroworld, as against a microcosm, at a wave interference of identical length, but miscellaneous amplitude is possible sticking particles in unified agglomerate because of operation of law of a universal gravitation. Therefore macrobodies with the same wavelength can have in space (per unit mass) multiple value of an angular momentum S on a screw trajectory

S=S₀∙n                                                   (22.3)

at the expense of multiple value V_tR. In (22.3) n has the same sense, as in the formula (22.1). In a microcosm the sticking of free particles is impossible because of a coulomb repulsion is of the same name of charged particles and absence of attraction between "neutral" particles. Thus, in the formula (22.2):

S=V_tmR∙n                                                (22.4),

and V in a denominator it is makes sense progressive speeds:

V=V_f                                                   (22.5).

By substituting (22.4) and (22.5) in (22.2), we shall discover (22.1). A conclusion from here follows, that the central body will forms a satellite system by capture of space bodies with an identical wavelength, but multiple value V_tR of rather minimum value at n=1. Thus the constitution of a forming system follows the theory of the Bohr for atom of hydrogen with that difference, that "exited" orbits are steady, since the satellites have not a capability something to radiate for transition to more low-altitude orbit, that the system as a whole has passed in a condition with a minimum of a potential energy. From a constitution of a solar System and satellite systems it is visible, that "wavelength" of trapping bodies of earth group differs from "wavelength" of bodies jupiter of group, i.e. the solar system resembles two-electronic atom with two independent systems of energy levels macrobodies.

By substituting (22.3) in (22.2) and allowing, that

S₀=mV_0tR₀                                             (22.6),

and V_0t=V_f∙n, we shall receive:

R=R₀n²                                               (22.7),

That corresponds to actual distribution of planets or satellites at given "wavelength". Earlier we used the formula (22.7) on the strength from the observation facts, instead of theoretical calculations.

From an equilibrium condition of a space body on steady orbit it is easy to find a stability criterion of orbital motion, which one depends only on mass of a central body and does not depend on a quantum number of a space body:

RV²=GM                                                (22.8),

where R - radius of orbit, V - orbital velocity, G - gravitational constant, M - mass of a central body. From (22.8) it is possible to receive a wavelength, which one is immersed to the by given a central body, allowing, that =2∙R₀:

                                              (22.9).

As V₀ does not depend on mass of a central body, that was shown earlier, the satellite system will be formed by space bodies, for which one the wavelength is proportional to mass of a central body, is watched actually - as more than mass of a central body the further satellites are arranged.

Allowing above-stated, it is necessary to give more general words of motion of bodies: all free bodies are moves on a screw line. Thus we shall mean, that the tangential velocity of motion is peer a translational in microcosm, and in macroworld the tangential velocity is peer a translational only in the first quantum condition of a body.

22.1. Gravidynamic interplay and evolution of orbits

As is known, now there is no an explanation, why all planets move on orbits to direction of rotation of the Sun in one plane, why that most is made by members of spiral galaxies. Gravidynamic the interplay allows easily to explain both this fact, and many other features of a constitution of a solar System and miscellaneous kind of galaxies. We know, that of a like magnetic poles are repulsed, and unlike are attracted. From chapter 11.2.2 it is possible to guess, that of a gravidynamic poles act by an opposite image. At first we shall be defined in concept «pole». If the electrical or gravitational charge is gone so, that thus sweeps some area, we speak, that arises magnetic (gravidynamic) the moment having two poles, as shown in a figure 22.1.1.

On a figure the motion of positive electric charge on a circular orbit is figured at which one there is a magnetic moment and two magnetic poles - northern of N and southern S. At the same motion of a gravitational charge from an antimatter the picture of originating two of gravidynamic poles is similar. Apparently, that orbital the gravidynamic moment 1 is much greater own of the gravidynamic moment 2, since the value of these moments is determined by product of gravitational «current» on the area, swept by it, under the formula:

                                                               (22.1.1),

where: K - coefficient, value which one considerably increases at nearing a running speed to light speed because of the same increase of a gravidynamic field (see chapter 11.1),  - gravitational «current», where V - running speed of a gravitational charge , r - radius of orbit or effective radius of proper rotation of a space body.

Because of mutual attraction of the gravidynamic moments 1 and 2 proper rotations of planets take place in a direction of their orbital motion and in a sense of rotation of the Sun. The exceptions of this conclusion will become soon clear. 

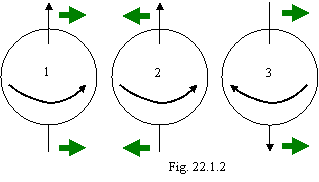
As will interact of gravidynamic poles among themselves it is visible from a figure 22.1.2.

Closer arranged to each other parts of charges № 1 and № 2 move counter and are attracted, and the arranged closer to each other parts of charges № 2 and № 3 move in one direction and are repulsed pursuant to the concepts of operating of a gravidynamic field set up in chapter 11.2.2. Therefore like of a gravidynamic poles are attracted, and unlike are repulsed from each other.

On a figure 22.1.3. the motion of some space body before acquisition by its Solar System is shown. Apparently, that the acquisition can take place in any phase of this motion. Thus it is important to mark, that arisen elliptical orbit in any case will be arranged bevel way, approximately, 45⁰ to a screw trajectory, and the direction of proper rotation of a body will be kept invariable because of a gyroscopic effect. Thus, the entrapped body is gone in a solar System under any arbitrary angle to an equatorial plane of the Sun, which one is determined not only phase of motion at the moment of acquisition, but also initial direction of an axis of a screw trajectory of a «free» space body. Therefore and the direction of proper rotation can be arbitrary. However, all this is fair in the initial moment after acquisition. In further orbital plane is turned so that the orbital motion was to straight because of attraction like of gravidynamic poles of the Sun and orbital of the gravidynamic moment. The sense of rotation too aims to become to straight (in the side of orbital motion), but the gyroscopic effect strongly precludes to this, therefore turn of rotation axis takes place considerably slower and is accompanied by precession of this axis. The considerable temporary difference in evolution of orbit and rotation axis allows to judge a possible direction of incoming of a body in a solar System and about time of this incoming.

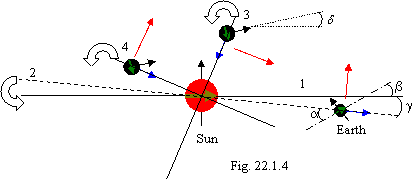
On a figure 22.1.4 the part of a solar System in an equatorial plane of the Sun 1 is shown. For orientation the broken line shown a plane of an ecliptic 2 (orbit of the Earth), and the dash-and-dot line shown an equatorial plane of the Earth. The angle  is peer 23,45⁰, the angle  is peer 7,2⁰, then the angle  is peer 16,25⁰. The cyan arrows shown a direction of orbital motion, and the red arrows demonstrate a direction of the orbital gravidynamic moment for given orbit. Apparently, that in this case, the slopes of planes of planet orbits and of other members of a solar System in relation to a plane of an ecliptic are necessary for re-count in relation to an equatorial plane of the Sun, since just it urges all the gravidynamic moments orbital and own to upbuild in a direction own of the gravidynamic moment. The position of a body after acquisition depends on its position on a screw trajectory at the moment of acquisition and angle  between rotation axis of a body and equatorial plane of the Sun. If, for example, the body was grasped in a distant point, where it is figured on a figure 22.2.3, after acquisition orbit of a body will take a position 3, and if is grasped in a hither point, after acquisition orbit of a body will take a position 4. In the beginning after acquisition orbit of a body frequently will have except for a large eccentricity also large angles of inclination to an equatorial plane of the Sun. In a position 3 body have return orbital motion and reverse rotation, but in outcome of gravidynamic interplay with the Sun orbit will be turned counter-clockwise (is shown white arrows) and eventually motion of an entrapped body will become «normal» - direct circulation and direct rotation not a hundred miles away of a plane of a solar equator. In a position 4 body at once have to straight motion and rotation, therefore of large turn of orbit it is not required. At turn of orbit the figure axis of rotation remains in space invariable as for the gyro, therefore turn of this axis considerably lags behind on time orbital turn. At desire, the reader can explicitly consider outcomes of acquisition of dextrorotary and laevorotatory space bodies approaching under different angles to an equatorial plane of the Sun and to receive of the characteristic of any member of a solar System. The case is specially interesting, when after acquisition the motion of a body becomes to straight, and proper rotation a converse. In this case the gravidynamic interplay is forced to brake rotation of bodies, and then to urge to be gyrated in a forward direction. By results of such qualitative analysis it is possible to judge not only approximate acquisition timing, but also about a direction, whence space body to us has come.

22.2. Two large errors: Newton first law and inertial reference systems

Let's consider motion of a free body. Official physics considers, that this motion obeys to the first Newton's law and, while, nobody doubts of it, except for me. In chapter 2 the valid thought is adduced of the doctor M.L. Klebanov, which one can be formulated so: «any free body is not free from own mass». Let's suspect, that some body (microparticle or macrobody) imparted some speed V. Generally direction of velocity vector of a body and direction of an axis of its rotation are arbitrary, that is shown on a figure 22.2.1.

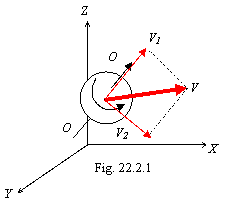The velocity vector on two orthogonally related component is decomposable: V₁ on a direction of rotation axis of a body and V₂ of perpendicular this axis.

Under the theory of new physics the gravidynamic field arises at any motion of gravitational charges. Rotated mass is look-alike to a contour with gravitational «current» creating induction of the gravidynamic field B, directional lengthwise axis rotations. Thus, the situation becomes similar to motion of electric charge perpendicularly to magnetic field. On a body acts gravidynamic clone of force of the Lorentz urging it to move on a circumference (clockwise if to look lengthwise axis rotation). The second independent motion takes place uniformly lengthwise axis rotations of a body, since thus the gravidynamic effect is equal to zero point. Thus, any free body is gone on a right-handed or left-handed trajectory depending on a mutual direction of vector of proper rotation and vector V₁. The body figured on a figure 22.2.1 will move on a right-handed trajectory. As it is a consequent of screw motion of free bodies expressed in them «a wave-corpuscle dualism», possible to assert about an inaccuracy of the first Newton's law and principled absence «of inertial reference systems», since the screw motion is absolute. For not free bodies the roundabout is saved, and translational, naturally, fades, being transformed in potential energy of universal repulsing (chapter 1).

For the same time the body passes a path, equal «to a wavelength de Broglie» in a translational motion and some circumference in a tangential rotation about an axis of a screw trajectory. This length makes an integer of lengths of waves in a translational direction (on orbit the integer «of wavelength de Broglie» is stacked), therefore we can record:

                                                            (22.2.1),

whence:

                                                          (22.2.2).

In chapter 20 is shown, that orbital radius of space bodies is proportional to a square of integers, starting from a ground state with minimum radius of orbit, therefore from (22.2.2):

                                                             (22.2.3).

Apparently, that the common energy at screw motion is peer to the sum of kinetic energy of translational motion and potential energy of universal repulsing (chapter 1) on a circumference of cross section of a screw trajectory:

                              (22.2.4).

In view of last expression, the formula (22.2.3) will be recorded so:

                                                                 (22.2.5).

There is a problem: why the ratio of potential energy to kinetic before capture of space bodies from a screw trajectory on a circular orbit has only integer values from unit and above? Alone explanation I see that space bodies, having identical value the Vr product, have also identical «a wavelength of de Broglie» therefore are capable to be integrated among themselves («to interfere») at long-lived travel in space spaciousnesses. The law of an equal energy distribution on degree of freedoms requires equalling V₁ and V₂, i.e. n=1, but depending on induction of a gravidynamic field of the given body plus the gravidynamic clone of force of the Lorentz reduces radius of a screw trajectory simultaneously augmenting potential energy not influencing on kinetic energy of a body. It would be possible to compose the formula, make something out of thin air, depicting the integer values n for a meteoritic and cometary material, but I it to do shall not be, leaving the solution of this problem for the followers of new physics, which one at first will understand physical reasons integralness n, and then it is uneasy to write and applicable formula.

Now we shall consider motion of a not free body. The sceptic, by reading a beginning of the chapter, will consider it for delirium mad. Let's throw a rock along a surface of ground and any screw motion we shall not see. That he has understood essence of a problem, I shall remind, that at customary running speeds a gravidynamic field very weakly, therefore sizes of a screw trajectory have space scales. Besides if in a microcosmos the gravitational interaction does not influence at all on gravidynamic, in a macroworld the outcome of a competition between by gravitational and gravidynamic interplay depends on particular parameters of bodies. Thrown along a surface of ground the rock is not free any more, therefore can move at the end only on a circular orbit. That the Earth did not preclude with its motion, suppose, that at the moment of a throw it was tightened in a point in former center of the Earth and has not changed mass. Angular momentum of a rock concerning center of the Earth:

                                                          (22.2.6),

where: m - mass of a rock, v₀ - its initial velocity of motion, R - radius of Earth.

Energy of connection of a rock with the Earth:

                                                     (22.2.7)

is the algebraic sum of potential energy of attraction and potential energy of universal repulsing. G - gravitational constant, M - mass of the Earth, v and r current values of speed and radius of orbit. We suppose, that the rock ultimately will appear in a potential well, i.e. will take a fixed circular orbit, therefore it is necessary to find a minimum (22.2.7). But before it is necessary to express a running speed through radius of orbit. Using a law of conservation of angular momentum of a body, is similar (22.2.6) we can record:

                                                           (22.2.8).

By substituting (22.2.8) in (22.2.7), we shall discover:

                                                   (22.2.9).

Let's discover a minimum (22.2.9):

                                                 (22.2.10),

where: r₀ - radius of a fixed circular orbit, - constant, =vr, since m remains to a constant.

Substituting in (22.2.10) numerical values at v₀ = 10 m/sec, we shall discover, that if the Earth did not hinder motion of a rock, it would take a circular orbit around of its center of radius 10.2 meters. The speed of its motion on this orbit will be 6250 kms/sec.

Now it is necessary reply to a question: why almost all microparticles have the same moment on a screw trajectory equal ? Though official physics separates bosons from fermions, nevertheless, at definition of «wavelength» those and others uses a de Broglie formula, which one envisions an angular momentum by their identical, divergences with experiment in definition of «wavelength» of these particles differently will be received. Therefore constant of the Planck h is not «quantum of action», as official physics considers, and ordinary angular momentum of a particle:

                                                     (22.2.11),

and this moment refers not to an own moment, and to a moment on coils of a screw trajectory, which one is significant more own moment. From (22.2.10) we shall express radius of a screw trajectory of a particle through its speed:

                                                         (22.2.12),

where  not a fine structure constant, and constant of product vr at change of these multiplicands, when mass of a body at this change remains to a constant, therefore (22.2.12) - direct consequent of a principle of conservation of moment of momentum of a body.

From that fact, that the value  of planets of a solar System is augmented with increase of spacing interval from the Sun (chapter 21, the figure 21.3) is possible to draw a conclusion, that  is inversely proportional inductions B of a gravidynamic field:

                                                         (22.2.13).

If for space bodies the counting of induction of a gravidynamic field lengthwise axis their proper rotations is intricate because of miscellaneous rotation rate, miscellaneous density of a material of space bodies and their miscellaneous value, for microparticles this calculation is considerably simplified. The components of microparticles move with speed of light, therefore create the greatest possible induction of a gravidynamic field lengthwise axis their orbits. Therefore it is possible to record:

                                                         (22.2.14),

Where - specific induction of a gravidynamic field of a unit mass, and m - particle mass. By substituting (22.2.14) and (22.2.13) in (22.2.12), we shall discover:

                                                       (22.2.15).

Number of dimension of gravidynamic induction in a system CGS: [B] = sec×cm^-2,

and Number of dimension of specific induction [] = erg^-1×sec^-1.

To receive an angular momentum of a particle on coils of a screw trajectory, we shall multiply (22.2.15) on mv:

                                                     (22.2.16).

Thus, we have found out one more physical sense of a constant of the Planck (angular momentum of a particle). As it happens, it is peer to reverse value of specific induction of a gravidynamic field and for all particles has the same value, since their components move with identical speed of equal speed of light.

Comments of the author to chapter 22.2:

1. Critical view on Newton's laws.

The first Newton's law. «Free bodies move uniformly and rectilinearly». In chapter 2 is shown, that any free bodies move on a screw trajectory, therefore first Newton's law is not applicable to the  body, but to a mathematical abstraction - axis of a screw trajectory of a body.

The second Newton's law. «F=ma - acceleration gained by a body, proportionally to force operational on a body, and in inverse proportion to mass of a body». It is easy to show, that in some cases the second Newton's law results in absurd outcomes. Let's act with force 1 dyne on an electron of mass 9,1×10^-28 g. At the end of the first second on the second Newton's law the electron should achieve speed more speed of light in 3×10¹⁶ times. Apparently, that the second Newton's law should be agreeed relativistic increase of mass of a body, for example, so: 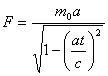, where t - valid time of force F on accelerated mass, which one reposed.

The third Newton's law. «The Operating is equal to counteraction». In chapter 1.2 the analysis of experiment is given, when the mass throw on a cushion. In it is shown, that the third Newton's law is correct only in conditions of absence of inertias force in a condition static or dynamic equilibrium.