21. THE THEORY of CAPTURE of SPACE BODIES
|
|
|
|
|
|
Concerning capture of one space body by another the
modern cosmology gives the unequivocal answer - it is impossible without
presence of the third body. The explanation is very simple. The gravitational
energy interaction of bodies is transformed into a kinetic energy of
"falling" them against each other. If a trapping body it is little as
contrasted to arresting (central), the trapping body will describe around of a
central body a parabolic trajectory and again will leave in perpetuity. The
main reason of impossibility of capture is, that the trapping body is incapable
by any way rather fast to lose exuberant energy. The energy loss is possible
only at the long-lived revolution around of a central body under activity of
tidal and other forces, which one all are together too small for embodying
capture at once. The change of a potential energy of two bodies, interacting at
the expense of a gravitation, how it itself is introduced by a modern cosmology
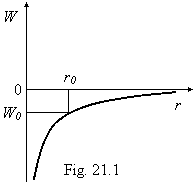
is shown on a figure 21.1.
In any point r0 a potential energy of a body m
(the central body M is in point of origin), equal W0 is simultaneously peer to a
kinetic energy of a body m, that requires an energy conservation law
(common energy is peer to zero point). Therefore in any point a body m
capable "to recoil" on indefinitely large distance from M and
its capture is impossible. "Within the framework of a gravitational problem
of two bodies capture or outbreak are impossible, as there are absent factors
which are capable to change a full mechanical energy of bodies". Physics
of space, "Soviet encyclopedia", М., 1976, page 74. That the capture has taken
place, the body m on indefinitely large distance from M should
have negative energy, that physically it is impossible, since the potential
energy m this condition is peer to zero point, and the kinetic energy is
always plus. Is received that the body belonging to a solar System has some
total energy having negative value, therefore it can not abandon a system
(outbreak is impossible). The body not belonging to a solar System has some
total energy (kinetic) always having positive value; therefore it can not be
captured. Thus, from a point of view of modern science, any space system is
isolated in relation to a mass transfer. To straight lines a corollary it is
the conclusion that all bodies belonging to a solar System, belonged to it
always, therefore, the solar System could be formed only simultaneously and of
one protoplanetary of a cloud.
The reasoning of the
orthodoxes in a considered problem are so convincing, that it should seem,
alternative by it does not exist. However observation data, for example,
backward motion of some satellites, reverse rotation of some planets, constant
clearing of interplanetary dust, meteorites both comets and set others with all
evidence display an inaccuracy of notions of an official cosmology, both
concerning formation of a solar System, and concerning the theory of a
gravitational interaction as a whole.
New physics
absolutely on diverse imagines gravitational interaction of two bodies. The
potential energy of connection of these bodies sums up of a potential energy of
attraction and potential energy of repulsion:
(21.1).
Allowing a law of conservation of
angular momentum, which one for invariable mass will be:
Vr=
(21.2)
and
substituting (21.2) in (21.1), we shall receive:
(21.3).
Differentiating
(21.3) on radius and equating a derivative to zero point, we shall discover
radius of orbit, at which one the binding energy has a minimum:
(21.4).
By substituting
(21.4) in (21.3), we shall discover a binding energy of two bodies:
(21.5).
|
|
|
|
|
|
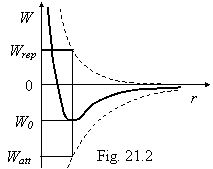
The change of a potential energy is shown on a figure
21.2.
As it is visible from
a figure, the body m will be moves around of a central body on a steady
circular orbit of radius r0,
since the system thus has a minimum of a potential energy. If m to
impart some additional energy not superior that is determined by the formula
(21.5), orbit will become elliptical. If the exuberant energy will be peer to a
binding energy, orbit will become parabolic and the system will be destroyed
because of removal m in perpetuity. The energy conservation law in case
of capture is executed for the reason, that half of energy of attraction passes
in energy of a repulsion and to delete m in perpetuity, it is necessary
to impart this body energy, defined expression (21.5), i.e. second half,
therefore common energy on infinite removal of bodies from each other again
will become zero. Thus, the capture is unavoidable for any body, if its kinetic
energy on indefinitely large distance from M does not exceed a binding
energy (21.5) on steady orbit.
Let's
suspect, that on indefinitely large distance from M the body m
has a kinetic energy Ek component some share K from a
binding energy W0 on the future circular orbit:
(21.6).
Then
the equation (21.3) can be recorded so:
(21.7).
Substituting
(21.6) in (21.7) and allowing ratio (21.4) and (21.5), we shall discover the
formulas for a perihelion and aphelion of orbit:
(21.8),
(21.9).
Equating
(21.8) expression (13.19), we shall discover an eccentricity of orbit:
(21.10).
The
formula (21.10) displays that again captured bodies have orbits with large
eccentricities. For example, the body having a kinetic energy in perpetuity
component only 1 % from a binding energy, on a circular orbit will have an
eccentricity equal 0,1. If in the formula (21.10) to substitute (21.6), where 
, and also (21.4) and (21.5) and to take into account,
that =r0V0,
where V0 - orbital velocity on a circular orbit, we shall
receive one more formula for an eccentricity of orbit of a captured body:
(21.11),
where: 
-
velocity of a body m in perpetuity,
V0 -
velocity of a body m on a circular orbit, which one it will take after
full consumption of exuberant energy Ek.
Let's consider mechanism a capture
and evolution of orbit of an captured body in more detail.
Let's
suspect that the body is gone in a solar System with an eccentricity equal 1.
On modern notions this body, pass the perihelion of orbit, will be deleted again
in perpetuity and can not be captured. On notions of new physics such motion of
a body is equivalent to "impact" with a solar System and recoil of a
body back. Thus on a law of conservation of momentum the body will transmit a
part of the impulse to a solar System as a whole and the back branch of a
trajectory will represent any more parabola, and the ellipse, i.e. eccentricity
of orbit will appear less than 1. Thus, the body will appear captured and, at
each passage of a perihelion, it will transmit to a solar System of a portion
of the exuberant energy so long as orbit of a body will not become circular.
Apparently, that for this purpose the speed n around of the Sun should
be infinite, since the transmitted portions all time decrease. Therefore system
of energy levels of an captured body is very similar to a system of energy
levels of atom (see chapter "Theory of a hydrogen-like atom"). The
circular orbit in these cases is reached at n
. Here it is necessary
to update, that the circular orbit can be reached neither in a hydrogen-like
atom, nor in a space system. Therefore it is possible to speak only about some
equilibrium orbit, close to circular, since in both cases the exited state
arises at slightest effect at a system, as the levels of energy near to a
circular orbit most are close set. In first case the atom is in an exited state
even at temperature of absolute zero, and in the second case the exited state
of space bodies is supported to constant by falling out on them of meteorites,
comets and cosmic dust.
On a law
of conservation of impulse:
(21.12),
where: m
- mass of a trapping body,
Vf - "exuberant" velocity m
"forward",
Vb - "exuberant" velocity m
"back",
M - Mass of an arresting body,
VM - velocity gained M.
In
(21.12) mass of the remaining terms of a system we leave out, otherwise under M
it is necessary to understand total mass of a system.
The
energy balance:
(21.13).
Deciding
in unison (21.12) and (21.13), we shall discover:
(21.14).
From
(21.14): 
, 
etc., therefore, for speed n the formula
(21.14) starts a kind:
(21.15).
By substituting
(21.15) in (21.11), we shall discover change of an eccentricity:
(21.16).
By
addressing to the formula (20.1.6), it is possible to explain to it as well by
that the small masses lose less energy on each revolution and longer save a
large eccentricity of orbit. The evolution of orbits of large masses happens
much faster.
In
(21.16) at n=0 (the capture still is not present) e=1, and at n, e0,
since the fraction in (21.16) always is less 1.
The third
Kepler's Law can be conversed to a kind:
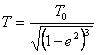(21.17),
where: T
- period of rotation on elliptical orbit,
T0 - period of rotation on a circular orbit,
e - eccentricity.
The
energy loss of a body m on each revolution around of a central body M
will make:
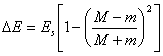(21.18),
where: Es
- "exuberant" energy of a body m.
Using the formulas (21.16) and
(21.17) it is easy to count up evolution of orbit of a captured body. For a
simplicity, masses of bodies we shall consider invariable for a period of
evolution.
Moon. Before capture by the
Earth, moon should have
value a almost same, as for the Earth, that equilibrium radius of its orbit
around of the Sun was close to earth radius. Moon before capture by a solar
System could not have velocity of 30 kms/sec and e=1, since after
passage of a perihelion, its eccentricity remain too large (e=0.99999992614)
and first revolution around of the Sun it would commit 17.6 billions years. In
this case capture of moon by the Earth is impossible, except for a random
direct hit. The velocity of moon in perpetuity less than 30 kms/sec, for
example 20 kms/sec is more interquartile. In this case orbit of moon in a solar
System will have an initial eccentricity 0.667 with orbital period 2.4 years.
In two opposite points on a line, perpendicular main axis of orbit and passing
through center of the Sun, orbits of the Earth and moon will be intercrossed.
Near to these points the capture of moon by the Earth is possible. Now
equilibrium eccentricity of orbit of moon makes 0.0549 and average speed of
orbital motion about 1 km/sec. Let's suspect that in a start of capture moon
had the same velocity concerning the Earth, i.e. being moves to the Earth on a
parabolic trajectory, moon after passage of pericentre will gain an elliptical
trajectory around of the Earth with an eccentricity 0.9757. The period of the
first revolution around of the Earth will make 7 years, on the second
revolution the eccentricity of orbit will be diminished up to 0.952, and period
till 2.6 years etc. The stable orbit close to modern will be reached for 120
revolutions and on it is required all about 25 years. Such fast evolution of
orbit of moon is connected to its large mass concerning the Earth.
Earth. If to consider, that
the Earth before capture had velocity of 30 kms/sec (e=1), after the
first passage of a perihelion the eccentricity of its orbit will become equal
0.99999399, and the time of the first revolution after capture will be 24
million years. On the second revolution e= 0.99998798 and T=8.5
millions years etc. The equilibrium eccentricity of orbit will be reached for
800000 revolutions, approximately, behind 102 million years.
Considerable
mass of a satellite in relation to a central body and considerable eccentricity
of its orbit is necessary for check of set up views on evolution of orbits. In
a solar System there are two candidates for check: a Mercury and Nereid
(satellite of
Nereid. Under the literary data
(E.N. Sluta etc. Comparative planetology.
The
rather fast evolution of orbit is possible only for captured bodies, mass which
one not less than 10-7 mass of a central body. The less massive
bodies "recoil" from a central body practically without energy loss
and the evolution of their orbit are stipulated by other reasons:
1. All
bodies of a solar System are subject to activity of "solar wind". At
motion on elliptical orbit towards to "solar wind" the loss of
exuberant energy exceeds its entry at removal of a body from the Sun.
2. The
exact same mechanism is acts at a body irradiation by photons which are radiated
the Sun. At motion towards to the Sun the body immerses more short-wave
photons, than at motion from the Sun.
3. The
comets represent ice lumps from a water, ammonia and methane with
"stuffing" from meteoroids. Therefore comets rather fast fail under
activity of irradiation both tidal action of the Sun and their orbit rather
fast evolved. In the total from comets there is a meteoric swarm, in which one
the evolution of orbits of separate bodies depend on their mass.
In all
these cases at each revolution around of the Sun the body loses a portion of
exuberant energy, and its orbit comes nearer to circular.
1. The
flow of protons of "solar wind" near to the Earth makes ~2.5 protons/cm2×sec, and velocity it 400 kms/sec
(Physics of space. М., 1976, page 555-556). The asteroid of radius r,
driving in neighborhoods of the Earth on elliptical orbit to the Sun will meet
"solar wind" with velocity of 430 kms/sec, and at motion from the Sun
- 370 kms/sec. The loss of an exuberant kinetic energy of an asteroid for one
second will make:
(21.19),
where: S
- sectional area of an asteroid (m2),
mp - mass of protons
falling in one second on 1m2 of cross section of an asteroid (kg).
The full exuberant energy of an
asteroid driving with an eccentricity equal 1 in neighborhoods of the Earth
will make:
(21.20),
where: m
- mass of an asteroid (kg),
V - velocity of an
asteroid (30000 m/sec).
Density
of a material of an asteroid we shall accept equal 3000 kg/m3. By
dividing (21.20) on (21.19), we shall discover time of full loss of exuberant
energy of an asteroid. Thus it will be moves on a circular orbit. Here we do an
appreciable error in calculations, since (21.19) depends on a position of an
asteroid on orbit. The precise calculation is impossible, therefore it is
necessary to consider the received below formula only as first approach:
T=1.794×1016×r
(sec)
(21.21).
The
asteroid of radius 1 m under the formula (21.21) will take a circular orbit
behind 568 millions years, and mote of radius 1 micron for 568 years. During
existence of a solar System (5 billions years) to lose all exuberant energy at
the expense of this effect the asteroids with radius less than 10 m could only.
Therefore bodies of the greater size having a small eccentricity of orbit could
be captured with rather small initial velocity.
2. In the
chapter "Driving in vacuum the spectator, the source is immobile" the
formulas for frequency of light are received perceived by the spectator, moved
to a source: 
and from a source: 
. The difference of energies of photons perceived by a
space body, which one will be expended for decreasing of exuberant energy of
this body will make:
(21.22).
The solar
constant is peer 1400 watt/m2 (Physics of space. М., 1976, page
551). If the space body is gone near to the Earth with parabolic velocity of 30
kms/sec, with the registration (21.22) on each revolution around of the Sun
power of energy loss:
(watt)
(21.23),
where r - radius of a body.
By dividing (21.20) on (21.23) we
shall receive:
T=2.04×105×r (years)
(21.24).
The
formula (21.24) displays, that under activity of photon radiation of the Sun
the evolution of orbit of a space body flow past much faster, than under
activity of "solar wind". The same asteroid of radius 1 m will take a
circular orbit not through 568 millions years, and in 204000 years.
The
satellites of planets at motion on a circular orbit have not exuberant energy,
but all the same permanently lose energy on the enunciated mechanism, since are
moves that to the Sun, from the Sun therefore above-stated calculation for
satellites of planets appears more precise. For example, moon will lose
completely all energy of orbital motion (velocity of this motion of ~1 km/sec) for 11.8 billions years.
Naturally, that it will fall on the Earth much earlier than full energy loss.
Now becomes understandable, why for a Mercury and Venus are not present
satellites, the energy loss in their neighborhoods so is significant, that the
long-lived existence of a satellite is impossible. Moon exists as a satellite
only at the expense of the huge sizes and rather recent captured by the Earth.
For Mars and farther planets the solar constant is so small that the long-lived
existence of satellites is becomes possible.
Now we shall look, as
the enunciated new notions will be agreed practice of start of artificial
satellites, i.e. with a inverse situation, when the body m does not approach
with M, and is thrown out from it. It is known; see, for example, B.M.
Javorsky, A.A. Detlaph. The manual on physics, "Science", М., 1964, page 79, that m has
become a satellite M, it should be imparted the first solar escape
velocity:
(21.25),
where R -
radius of a central body. For removal m in perpetuity it is necessary to
impart the second solar escape velocity (parabolic):
(21.26).
On a surface of a
central body, the body m has a potential energy of attraction 
. That m has appeared in a potential well on orbit around of a
central body, is apparent (see of fig. 21.2), that is necessary to impart it a
potential energy of a repulsion 
, equal half of potential energy of
attraction:
(21.27).
Conversing (21.27),
we shall receive (21.25). To throw out m on indefinitely large distance
(second solar escape velocity), it is necessary to it to impart a potential
energy of a repulsion, equal potential energies of attraction (that the common energy
has become to equal zero point):
(21.28).
From (21.28) we shall
discover (21.26).
Thus, new physics, line up with
official science concerning outbreak, about capture has opposite notions.
|
|
|
|
|
|
From (21.4) shall discover expression for :
(21.29).
For a solar System
(21.29) will look like:
cm2/sec
(21.30).
The relation to
integers (quantumness of values ) is shown on a figure 21.3.
|
|
|
|
|
|
It is easy to show, that all planets and satellites
in a solar System moves with the first solar escape velocity relevant to radius
of their orbit. For this purpose, for example, we shall substitute value =V× r
in (21.4) and we shall receive (21.25). Allowing (21.25) also that r= r0× n2, is easy to receive a
ratio: 
, which one displays, that the orbital
velocity of planets or satellites of "earth" group or
"jupiter" of group decreases in process of removal from a central
body in an integer of times concerning velocity in the first quantum condition.
Decreasing of centrifugal velocity of an electron at radiation of photons and
formation of atom also in an integer of times (the formula (13.15)) indicates
not only the family ties electrostatic and gravitational fields, but also on
scale independence of their activity, i.e. generality of the laws macro and
microcosm.
On a figure 21.4
points mark orbital velocities of planets of a solar System and their
satellites (under the data: E.N. Sluta etc. Comparative planetology, М. "Science", 1995)
depending on reverse value of their quantum number. On the basis of above-stated,
each group of satellites should lie on a straight line; the tangent of a slope
angle numerically is peer by which one of an orbital velocity of the term of
this group the first quantum condition, i.e. V0.
The straight lines are held on earlier received values a0 and r0
for each group, by dividing one on another. As it is visible, apparent
velocities of space bodies it is good "lie down" on straight lines.
Near to straight lines the title of groups, for example is indicated: the
sun(E) - Earth group of planets, and Jupiter(J) - satellites of Jupiter
"jupiter" of group.
It
is interesting to consider numerical values V0:
Planet
V0 km/sec
Planet
V0 km/sec
Neptune (J)
3.53
Neptune (E) 45.39
Jupiter (J)
7.12
Jupiter (E) 68.13
Saturn (J)
16.52
Saturn (E) 101.92
Sun (J)
27.80
Sun (E) 146.14
Uranus (J)
34.69
Uranus (E) 380.5
V0 "jupiter" and
"earth" groups though correspond each other, but is unexpected in any
way correspond with masses of their hosts. To be disassembled with this
interesting phenomenon shall put values of quantum numbers:
Planet
"jupiter" "earth"
Jupiter
1,2,3
2,3,4,5,6
Sun 2,3,4,5,6 3,4,5,6
Saturn 2,3,4,5,10 5,6,7,8,9,10
Uranus 4,5,6,7,9,11 35,36,37,38,39,40,41,42,43
|
|
|
|
|
|
Except for the Sun, the large quantum conditions correspond large V0, but on fig. 20.4 maxima on a
distribution curve of large comets and asteroids are traced down to a quantum
number 10 for Earth group (vertical thin arrows), and the quantum numbers of
Jupiter group are quite possible up to values, large 10 for yet not unclosed
"planets". In this case Sun in a list will move below than Saturn and
the sequence completely will correspond to sequence for V0. To add in the Sun in this list it
is not absolutely correct, but the justifying can be served by deep reliance of
the unified mechanism of formation of space systems.
The
absence of a correlation between mass of central space bodies and V0
of their satellite systems is additional affirming that the solar System (as
well as other sidereal systems) was formed at the expense of affixing of planets
already having almost off-the shelf satellite systems. They were shaped in
interstellar medium in different conditions of relative velocities of a central
body and flying by its potential satellites. If their velocity is rather great
to form a system the satellites with large values of a quantum number (as for
Uranus) can only, if this velocity is small, the system will be formed
predominantly by bodies with low values of a quantum number (as for Neptune).
Apparently, that the last case is more interquartile, therefore low values of
quantum numbers most frequently meet. Therefore all bodies of a solar System
having large quantum numbers (for example, comet with a large eccentricity),
for sure arrived to us from apart, instead of from the proximate interstellar
environment of the Sun. It brightly demonstrates to us Uranus with the
satellite system. A phenomenon of Uranus to explain from orthodox stands
practically it is impossible.
The
reverse rotation of a satellite or planet demonstrates its capture practically
in the whole kind. There is it as follows (fig. 21.5 as "from above"
on a plane of a solar System 1-1):
The
left-handed body m in a direction of arrow is gone counter-clockwise.
Its own rotation happens in the same side, and the rotation axis is parallel an
axis of a screw trajectory of a body. After capture of a body, its orbit
evolves so that the direction of the gravidynamic orbital moment has coincided
with by the gravidynamic moment of a solar System as a whole. As the rotation
axis of a body saves the position in space, at the end of evolution of orbit
the body m will be moves in a plane of an ecliptic in a straight
direction, but the rotation around of a own axis will be the reverse. During evolution
of orbit we shall watch at first large eccentricity and large orbit inclination
to a plane of an ecliptic. Such parameters we see for Pluto, therefore, it
rather recently is captured by a solar System. Gradually these values decrease,
but the rotating axis of a body is saved in space; therefore captured bodies
with reverse rotation are characterized by a large inclination of equator to
orbital plane. This angle depends on an angle between an axis of a screw
trajectory of a body before capture and plane of a solar System. If this angle
is close to 900 (fig. 21.5а), an inclination of
equator will be close to 1800, as for Venus. If this angle is close
to 00 (fig. 21.5b), the inclination of equator to orbital plane will
close to 900 and the body on orbit will to be moves "lying
edgewise", as Uranus. Thus, the reverse rotation of planets or satellites
indicates capture of these bodies bodily. The circumvolution of numerous
satellites of Uranus in its equatorial plane in one side especially visually
displays, that Uranus was captured together with a own satellite system formed
in interstellar space.
Let's
compare enunciated notions to the observation data on loss on the Earth of
meteors. If the meteoroid is captured by a solar System from interstellar medium
with zero initial velocity, it will be moves (at the end) on a circular orbit
around of the Sun. If radius of orbit corresponds earth, the traveling speed on
orbit of this body will make, as well as for the Earth, about 30 kms/sec. In a
straight direction on this orbit the overwhelming majority of meteoroids and
only minor quantity - in an opposite direction will be moves. Apparently, that
the traveling speed of meteors to the Earth after will be zero, and towards 60
kms/sec. Apparently also, that the traveling speed of meteors in interstellar
medium near to neighborhoods of a solar System can not in accuracy equal
traveling speeds of the Sun on galactic orbit (250 kms/sec), i.e. they have
some initial velocity before capture. "As the solar System is gone of
rather interstellar medium with velocity of 20-25 kms/sec..." E.N. Sluta
etc., Comparative planetology, "Science", М., 1995, page 17.
We can find what
maximum relative velocity should be for an interstellar meteor, that it was
captured, for example, on Earth orbit. For this purpose we shall equate its
kinetic energy of a binding energy under the formula (21.5):
(21.31),
where rE - radius of orbit of the Earth.
From
(21.12):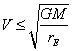 
(21.32).
The
formula (21.32) displays, that into given orbit the interstellar meteor having
initial velocity no more orbital (30 kms/sec for Earth orbit) can be capture
which one sums up with orbital. In this case orbit of a meteor will be
elliptical with an eccentricity close to unit, if in (21.32) to accept a sign
of equality. Thus, the velocity of drop on the Earth of meteors already to
belonging (captured) Solar System varies from 0 up to 30 kms/sec, if meteors
moves in a straight direction and from 30 up to 60 kms/sec, if they moves
backwards (towards to the Earth). If their velocity exceeds 60 kms/sec, the
similar meteors, depending on their velocity, can be captured into orbit of
Venus, of Mercury or hypothetical circum-solar planets in 1 or 2 quantum
conditions or their capture is absolutely impossible. For earth group of
planets radius of orbit of the first quantum condition is peer 0.6213×1012 cm. Substituting
this value in (21.32), we shall discover V=146 kms/sec. In a straight
direction these meteors will be moves in high layers of atmosphere with
velocity of 146 kms/sec, and in backward with velocity of 176 kms/sec. It is
necessary to consider similar meteors as the transit travellers, as they are
not capable to capture and it is necessary to consider falling out them on the
Earth as random "direct hit".
It is clear,
that transit meteors is an extremely infrequent case, since their relative
velocity is comparable to absolute speed of the Sun, i.e. they are the visitors
any more not interstellar, and intergalactic medium. The above-stated reasoning
are completely confirmed by observations.
"Wippl
has notified about measurements of velocities 144 meteors. 15 of these meteors
had velocities slightly more than 42 kms/sec... From 144 meteors observed by
Wippl, in one case it is impossible to consider demonstrated existence even as
one really of hyperbolic orbit". O. Struve etc., Elementary astronomy, М., 1966, page 188.
"Incidentally
same meteor shower has enabled Hey, Parsons and Stewart for the first time to
determine velocities of meteors on hyperbolic reflections (radar method -
V.K.). They have received value of 22.9 kms/sec, that will be well agreed with
determined of visual observations by value of 23.7 kms/sec.
Among
11000 meteors recorded within 847 clocks of observations since December, 1948
till March, 1950, the MacKinly has found only 32 meteors, the velocities which
one concerning the Earth slightly exceeded 72 kms/sec". Ibidem, page 190.
The falling out of
meteorites on the Earth in a plane of an ecliptic "outside", from a
direction, opposite from The Sun, west-to-east, i.e. after to motion and
rotation of the Earth is most possible. As the earth's spin axis is inclined to
this plane bevel way 23.50 that
depending from season, the falling out of meteorites is most possible in a band
of width from Southern tropic up to Northern tropic. In this connection is of
interest a hypothesis expressed by my higher son about ancient planetary
catastrophe as a result of drop on the Earth of a space body of the huge sizes
in region of the Philippine sea (near to Northern tropic when in northern
hemisphere there was a winter). In result (see, for example, the Small atlas of
a world, М., 1998, page
188-189) on the Earth was formed grandiose an impact crater of radius of the
order of 10000 kms enveloping practically half of terrestrial globe. The edges
of a crater have formed
In summary this chapter
is necessary to consider practically relevant problem of stability of orbital
motion of artificial satellites of the Earth. This problem because of huge
costs of their manufacturing and start is topical. Apparently, that for
maintenance of long-lived and reliable operation of an artificial satellite,
its orbit and orbital motion should be “natural”, i.e. the satellite should be
in one of quantum states, orbit should lie in a plane of an ecliptic, the
motion should be to direct, and satellite (or its part) to be gyrated in the
side of motion. All these requirements simultaneously it is impossible to
satisfy, but to be aimed to this it is necessary, if not we want to lose a
satellite “on unknowns to the causes”.
The
century riddle of structure of a solar System is resolved.
Mankind there are a lot of centuries unsuccessfully attempted to
understand, why the solar System is arranged so, instead of differently. Here
this problem is resolved with what I congratulate mankind.
In
chapter 11.2.5 is shown, that the product Vr = ? for a free space body is
determined only it by gravidynamic self-effect and remains to a constant at
orbital motion after capture of this body. Here we shall take advantage of the
formula (11.2.5.12) and table 11.2.5.1 from this chapter. Mean («standard») value /n
0.92×1019 cm2/sec
for terrestrial planets. Average value /n 4.82×1019 cm2/sec
for planets of jupiter’s group. Then the formula (11.2.5.12) can be copied so:
(21.33),
where 
- «standard» value . By substituting these values in
(21.33) for earth’s and of jupiter’s group, we shall discover radiuses of
orbits and, accordingly, orbital velocities in the first quantum condition:
, 
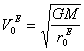(21.34),
, 
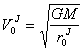(21.35).
Substituting
numerical values in (21.34) and (21.35), we shall receive:
=0.637×1012 cm, 
=14.44×106 cm/sec; 
=17.5×1012 cm, 
=2.75×106 cm/sec. Now it is
possible to substitute these values for calculation of radiuses of orbits and
orbital velocities of planets earth’s and of jupiter’s group:
rE=0.637×1012×n2, VE=14.44×106/n; rJ=17.5×1012×n2, VJ=2.75×106/n.
(21.36).
In table
21.1 the outcomes of idealized calculation and substantial values of radiuses
of orbits and orbital velocities of planets are shown.
Table 21.1.
|
Planet
|
Quantum condition |
Mean spacing interval from the Sun, 1012 cm |
Radius of orbit computed, 1012 cm |
Mean speed of orbital motion, 106 cm/sec |
Orbital velocity computed, 106 cm/sec |
|
Mercury |
3 |
5.791 |
5.733 |
4.789 |
4.813 |
|
Venus |
4 |
10.821 |
10.192 |
3.505 |
3.61 |
|
Earth |
5 |
14.96 |
15.92 |
2.979 |
2.407 |
|
Mars |
6 |
22.79 |
22.93 |
2.413 |
2.41 |
|
Jupiter |
2 |
77.83 |
70 |
1.306 |
1.375 |
|
Saturn |
3 |
142.8 |
157.5 |
0.964 |
0.917 |
|
Uranus |
4 |
287.2 |
280 |
0.681 |
0.687 |
|
Neptune |
5 |
449.8 |
437.5 |
0.543 |
0.55 |
|
Pluto |
6 |
591 |
630 |
0.474 |
0.458 |
Though the computational and observed parameters of planets differ, but
it is necessary to mean, that these parameters step-by-step change. Therefore
design values demonstrate the future characteristic of planets. For example,
the Earth in due course will be eliminated from the Sun, approximately, on 10
millions kilometers, and Venus will approximate, approximately, on the same
value.
It is interesting to learn radius of a screw trajectory of a planet in a
free condition before capture. Apparently, that it will be in n2
more being of radius of orbit. For example, the Earth had radius of a screw
trajectory in a far space in 25 times more its orbital radius. Some bodies of a
solar System have a quantum number 10 and more, therefore, radius of their
screw trajectory in a free condition in 100 and more time exceeded observed.
The
product Vr for planets of the order 1020 cm2/sec,
and for satellites of planets on 5 orders is less. It means only one - position
of satellites of planets arise from of secondary capture. At primary capture of
space bodies by a solar System they are arranged, approximately, as planets
pursuant to density and quantum condition. Thus have Vr approximately
applicable to the proximate planet. As the relative velocities of potential
satellites and planet-host are insignificant and, besides they is close to each
other, at secondary capture and formation of a satellite system Vr of
satellites will be on some orders less. Thus, the solar System (as well as any
other sidereal system) is reshaped at the expense of primary capture of planets
and secondary capture of satellites. The mechanism of secondary capture is
completely similar to primary capture, therefore constitution of satellite
systems repeats a constitution of a solar System in a miniature. It is
interesting to mark, that bodies, enough far arranged from a planet, have
negative relative velocity (less speed of a planet), therefore can be grasped
into satellite orbit with a backward motion and rotation of a satellite.
In conclusion of this chapter it is possible to laugh at the orthodox
astronomers, which one recently «interdict» to Pluto to be called as a planet.
Fortunately, he about it still not knows.
Comments of the author to chapter 21:
1. Power analysis of capture.
I am given thanks to Serge Alekseev for a fruitful controversy about a
problem of capture as a result of which one I, at last, itself has understood
essence of this problem. At infinite spacing interval between a central and
capturing body the energy of a system is peer to zero point. During capture the
capturing body on a spiral approachs with a central body. Thus the attractive
force is inversely proportional to a square of spacing interval between bodies
because of operation of law of a universal gravitation, and the centrifugal
force of a repulsion is inversely proportional to a cube of spacing interval
between bodies because of operation of law of preservation of an angular
momentum. In outcome on some spacing interval from a central body these forces
are counterbalanced and the capturing body starts to move on a steady circular
orbit, since the further approach of bodies becomes impossible. Thus half of
gravitational energy by obtained system is consumed for a
repulsion from a central body, and the stayed half makes bond energy. In
outcome the system as a whole again has a zero-point energy, as well as on
infinite spacing interval. If to esteem energy only of captured body, its
positive energy of a universal repulsion exactly is peer to negative bond
energy, therefore its general energy too zero. At an inverse process of
deleting of an captured body on perpetuity, we shall overcome only negative
bond energy, but same on value the positive energy of a universal repulsion
will promote deleting of a body. Therefore on perpetuity the energy of a system
again will become zero.
If the capturing body on perpetuity already had some positive kinetic
energy (less depth of potential well), it after capture will move on elliptical
orbit with that exuberant energy with respect equilibrium, which one it had on
perpetuity.
2. Main error of an official cosmology in a problem of
capture.
The official cosmology, while, has not notion about screw motion of any
free bodies. This achievement of new physics, which one asserts, that all bodies
of the nature have an own angular momentum, which one is saved at their
interplay. Let's see at the formulas (21.4) and (21.5). From them it is
visible, that the potential well for an captured body will be formed in any
case. If an angular momentum of this body large, a steady circular orbit (the
bottom of a potential well) will be far from a central body, and bond energy,
accordingly, is small. And on the contrary. The official notions recognize that
a body before capture has not an angular momentum, i.e. is gone rectilinearly
to a central body. In this case capture is impossible, since the transformation
of half of potential energy of attraction to energy of orbital motion is
impossible.
3. Physical sense of the famous formula E = mc2.
All material bodies consist of «elementary» particles: an electron,
proton, neutron and some other. In section of the monograph «ELEMENTARY
PARTICLES» is shown, that all they consist of orbital motion of components with
speed of light, which one are retained on a circular orbit by gravidynamic
attraction. Also in chapter 1 the concept of universal energy of a repulsion is
entered, which one is gained by any body moved on a circumference. This energy
numerically is peer to «kinetic energy» of a body, but as such actually misses
so long as the body will not be eliminated on tangent to orbit. See at a figure
21.2. In application to elementary particles and with taking into account for
virial theorem here half of energy of gravidynamic attraction Watt
at formation of a particle is spent for bond energy of components
(mi c2/2), and second half on energy of a universal
repulsion (mi c2/2). So that to eliminate components of a
particle on perpetuity and to pay energy of components in zero point it is
required to expend energy Ei = mi c2. The
common rest energy (fixed) body will be E0 = m0 c2,
and common energy of a driving body E = mc2, where m - relativistic
mass of a body.
21.0.1 Elliptical orbits of space bodies
|
|
|
|
|
|
The circular orbits of space bodies are an extremely
infrequent case, when the exuberant energy of a body is completely depleted,
but it can take place only for infinite number of rotations on elliptical
orbit, when on each revolution the part of an impulse of a body is transmitted
to a system as a whole. Even the ideal circular orbit can be distorted under
influencing of the different space factors: tidal effect of the neighbours,
fall on a surface of meteorites and comets etc. Therefore all space bodies are
actually in an exited state, having some exuberant kinetic energy in matching
with its equilibrium value.
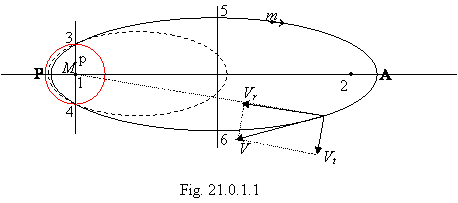
On a figure 21.0.1.1 elliptical orbit of a body m rotated
clockwise around of a massive central body M is shown. Spacing interval
between points P (pericenter) and A (apocenter) of orbit is equal
to a large axis of elliptical orbit (2a), and spacing interval between points 5
and 6 - small axis of orbit (2b). Spacing interval between focuses of orbit
(point 1 and 2) is equal 2c. During a gradual transfer momentum of a body m
to a system as a whole (actually, body M) there is a transformation of
elliptical orbit in circumferential (is shown red colour), but at this
transformation all orbits are intercepted in two inverse points 3 and 4 apart
of radius of the future circular orbit - focal parameter of an ellipse p
(see figure 13.2 in chapter 13). Thus, the evolution of elliptical orbit of a
space body a little than differ from evolution of orbit of an electron in atom.
Input datas for the subsequent analysis we have determined.
Apparently, that the law of conservation of angular momentum demands,
that in any point of orbit at any time down to achievement of a circular orbit
the angular momentum L bodies m concerning M should be
saved invariable:
L=mVt×r
(21.0.1.1),
where r - spacing interval from m up to M.
In spite of the fact that on each revolution the energy of a body m
decreases, for one revolution it is possible to consider a total energy of this
body in points of pericenter and an apocenter invariable. The total energy is
piled from universal energy of a repulsion (chapter 1):
(21.0.1.2)
and energy of a gravitational attraction to M:
(21.0.1.3).
Therefore total energy of a body m will be:
(21.0.1.4).
Rewriting (21.0.1.4) for pericenter and apocenter, equating them among
themselves, after some transformations, we shall receive:
(21.0.1.5),
whence it is possible to receive the formula for precise account of an
angular momentum of a body m on a position of pericenter and apocenter
of its orbit (or value large «a» and small «b» semiaxis of an ellipse):
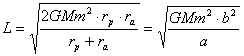(21.0.1.6).
By substituting in (21.0.1.6) numerical data for the Earth (E.N. Sluta
etc. Comparative planetology, М., 1995, page 78) we
shall find: L=25.974×1046 g×cm2/sec. If
to take advantage (21.0.1.1) and to substitute mean spacing interval from the
Sun and mean orbital velocity of the Earth, we shall receive essentially
distinguished value of an angular momentum of the Earth: L=26.632×1046 g×cm2/sec.
If we shall find a minimum of a function (21.0.1.4), we shall receive,
that thus the speed of a body m will be peer to the first cosmic
velocity:
(21.0.1.7),
and body will take a circular orbit. If we shall make that most for
spacing interval of pericenter of any elliptical orbit, it is easy to find
ratio of energy of a body on this orbit (E) of radius r to energy
of a body on a circular orbit (E0) of radius r0:
(21.0.1.8).
For parabolic orbit spacing interval of pericenter twice is less than
radius of a circular orbit (focal parameter), therefore energy of such body
twice exceeds energy on fixed orbit.
On ratio of radius of a circular orbit (focal parameter) to perihelion
spacing interval r it is possible to find an eccentricity of given
orbit:
(21.0.1.9).
Comparing 21.0.1.8 and 21.0.1.9, we can record other expression for
ratio of energy of a body on elliptical orbit to energy on a circular orbit
expressed through an eccentricity of orbit, which one can be determined more precisely:
(21.0.1.10).
Eccentricity of Earth orbit now 0.0167, therefore exuberant energy of
the Earth exceeds its energy in equilibrium state in 1.0167 times.
Allowing, that:
(21.0.1.11),
where p - focal parameter, and e - the eccentricity of
orbit, is possible to count up an angular momentum of a body or radius of a
equilibrium orbit, knowing these values.
The remaining details on motion of bodies on elliptical orbits can be
read in chapter 21.
Comments of the author to chapter 21.0.1:
1. Bond energy of an electron and space bodies on
elliptical orbits.
As electrostatic and gravitational interaction have not essential
differences, for further we shall take advantage of the data of table 13.1. The
major axis of orbit (2a) is peer to the sum of spacing intervals up to
pericentre and apofocus expressed through relative units r0 (radius
of a circular orbit):
n/(n+1)+n/(n-1)=2/(1-1/n2)=2a
(1).
But 1-1/n2=Etie
(2),
where Etie - bond energy on given orbit with a central body.
By substituting (2) in (1), we shall find: 1/Etie=a or, passing to
absolute values: E0/Etie=a/r0, whence:
Etie=(E0× r0)/a
(3).
Bond energy on any elliptical orbit appears inversely proportional
semimajor axes of this orbit, since product E0× r0 it is
identical all orbits.
21.1. That instigates earthquakes
When we viewed
orbital motion of an electron in a hydrogen-like atom, we have found out that
elliptical orbits are intercrossed with parabolic orbit and circular orbit in
two opposite points apart of focal parameter from a principal focus of orbit.
In these points component the velocity, directional to focus or from focus are
received with maximum value. This component is peer to zero point for strictly
circular orbit and points of a perihelion and aphelion of orbit of the Earth.
Making the same mathematical manipulations, which one we made at a conclusion
of centrifugal velocity for an electron in a hydrogen-like atom and allowing
the formulas, reduced in table 13.1, it is possible to record:
(21.1.1),
where: e -
eccentricity of Earth orbit (e=0.0167) and 
- binding energy of the Earth
and Sun, if the Earth would have a circular orbit:
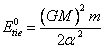(21.1.2).
Is received similarly
to formula (2.4), G – the gravitational constant, m - mass of the
Earth, M - mass of the Sun, a - product of a mean orbital velocity of the Earth on mean distance
from the Sun. By substituting (21.1.2) in (21.1.1), we shall discover value Etie=2.651386∙1040
ergs, and Etie0=2.652129∙1040 ergs. It is
understandable, that the actual binding energy of the Earth with the Sun is
less because of some exuberant mechanical energy of the Earth calling not
circular and elliptical orbit. It is possible to consider this exuberant energy
as:
(21.1.3),
where Vc
- velocity, directional on radius - vector to a principal focus. The numerical
value of this velocity from (21.1.3) is equal 499 m/sec or, approximately 0.5
kms/sec.
Thus, on
each revolution around of the Sun in perihelion (January 3-4) and in aphelion
(in by the beginning of July) the components velocities, directional to the Sun
and from the Sun are peer to zero point. In a start of April the Earth passes
one point of focal parameter and component velocity from the Sun is maximum,
and in a start of October this component is directed to the Sun and too is
maximum. Allowing, that the core of the Earth has enormous inertia and, as a
yolk in an egg, rest in magma, at acceleration and inhibiting action it
attempts to fall behind or, on the contrary, on inertia prolongs to be move to
the Sun. Thus it induces deformation of earth shells and instigates reset of
the previous pressure of earth crust or creation new. Allowing, that after
passage of a perihelion the velocity up to 0.5 kms/sec accrues faster, the
vernal earthquakes on the Earth should result in to more strong catastrophes,
than autumnal. Especially strongly described effect should be watched for a
Mercury with a large eccentricity of orbit, and also for satellites of planets
with large eccentricities.
Tidal effect.
Except for slugged motion of a core of the Earth all mobile shells
participate in this motion: atmosphere, hydrosphere and earth crust. On these
motions tidal effect of the Sun and Moon also is superimposed. If the tidal
motions of atmosphere and hydrosphere practically do not leave consequences in
states of stress of earth crust, and influence only ocean and atmospheric
flows, the tidal motions of the earth crust do not remain without
consequences in sense of provoking of earthquakes. Thus, it is possible to draw
a conclusion, that the tidal effect boosts instigating earthquakes in April in
night time, when the Earth leaves from the Sun and in October in daylight, when
the Earth comes nearer to the Sun and the inertia is exhibited to the greatest
degree.
21.2. Trajectories of
bodies at capture and gigantic atoms
|
|
|
|
|
|
In the monograph is shown, that all free bodies move
on a screw trajectory. It concerns, as to bodies of a microcosmos, and
macroworld. As the electrostatic interplay is similar to a gravitational
interaction because of an identical kind of the formulas of a law of universal
gravitation and Coulomb's law, for a determinancy, we shall esteem here
gravitational interaction shown on a figure 21.2.1.
|
|
|
|
|
|
The trajectory of a capturing body is shown from a
direction, perpendicular axis of a screw line. As approaching to central body
radius of a screw trajectory decreases, and the speeds tangential and
translational motion are augmented. Thus these speeds remain equal one another.
In the issue body appears captured on a circular orbit with parameters:
(21.2.1),
where: r0
- radius of orbit, =Vr, where V -
tangential velocity on a coil of a screw trajectory of a body, r -
radius of a coil, M - mass of a central body. Bond energy with a central
body W0 expresses by the formula:
(21.2.2),
where: G
- gravitational constant, m - mass of a capturing body.
From a figure 21.2.1 it is understandable, that the orthodoxes, while,
do not imagines an actual trajectory of a body at capture.
On
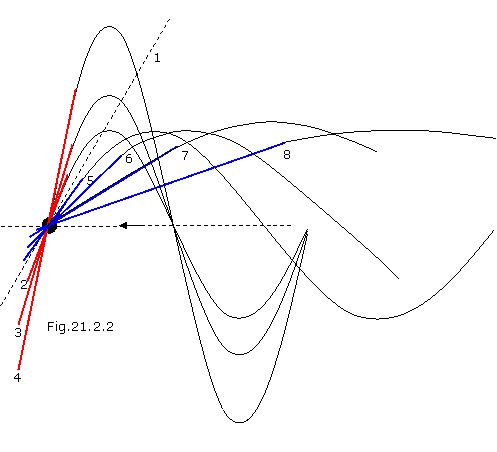
a figure 21.2.2 the trajectories of bodies on last coil before captue are
shown. Digit 1 shown a direction amounting with a direction an axes of a screw
trajectory the angle 
=450. All bodies having on
perpetuity zero forward speed after capture, will forms a circular orbit, the
plane by which one is inclined on an angle more than 450 to an axis
of a screw trajectory. With increase of a tangential velocity on perpetuity
(increase a) this angle grows, radius of a circular orbit also
grows pursuant to the formula (21.2.1). These trajectories are indicated by red
colour (2,3,4). If at the same
tangential velocity to augment forward speed of a body by perpetuity, after
capture there is elliptical orbit, the eccentricity is proportional to which
one translational (kinetic) energy of a body on perpetuity. The plane of
elliptical orbit makes with an axis of a screw trajectory an angle less than 450.
These trajectories are indicated by cyan colour (5,6,7,8). If this energy is peer to
depth a potential well pursuant to the formula
(21.2.2), the eccentricity becomes to equal unit and the capture is impossible.
The capturing body on a parabolic trajectory again leaves in perpetuity.
Capture
shown on a figure 21.2.1 we shall call as rigid capture. At such capture radius of a circular trajectory is minimum,
and the bond energy with a central body is max. With increase radius
of a circular trajectory is augmented, and the bond energy with a central body
decreases. Such acquisition we shall call as mild capture.
Gigantic atoms.
The
analysis of different versions of gravitational capture allows with success to
transfer conclusions of this analysis on an electron capture by atom. In
particular, us the mild electron capture will interest. Imagine, that we not permit to atom to capture an electron by version of
rigid capture, at which one at the expense of an electrostatic attraction of an
electron to a positive ion the screw trajectory of an electron considerably
decreases in the sizes. If to realise mild capture, obtaining gigantic
known atoms is possible. These atoms, by dimensions
from normal up to rydberg of atoms, will be stable as against last because the
valence electrons in them have a unique value of an angular momentum 
, instead of multiple, as in rydberg atoms, from which
one get rid at any capability. For implementation of mild electron capture it
is necessary them to hold by an external electrical field, which one accelerates
a positive ion and the electron brakes. If to pick up the conforming initial
velocities of ions and electrons, the mild capture can be executed at minimum
closing velocity of an electron with an ion. Thus radius of a screw trajectory
of an electron will be same large, as for a free thermal electron, accordingly,
radius of a circular orbit of a captured electron will be same large. In
chemical relation production of gigantic atoms is of interest, for which one
all valence electrons are captured by means of mild capture.
Production
of gigantic atoms and the synthesis from them of gigantic moleculas opens
indeed fantastic outlooks before chemistry, medicine, biology and technology. The capability of obtaining of any
given parameters of orbits of captured electrons is boundless dilates these
outlooks.
Let's consider, as an
example, activity of a power accumulator on the basis of gigantic moleculas of
hydrogen. Let's suspect, that the vessel by volume of
100 liters is filled by such hydrogen at normal conditions. At some small
heating of a part of gas the gigantic moleculas of hydrogen will begin to
dissociate on gigantic atoms of hydrogen, and last to be ionized, being
disintegrated on protons and electrons. Electrons we shall let in an
external electric network and is return in a vessel, where they again
incorporate with protons with formation already of customary atomic hydrogen,
which one will turn to normal molecular hydrogen. In all described processes
the energy is excreted except for a minor initial thermal impulse for start. It is interesting to count up fund of energy in a similar
power accumulator. Let's neglect the exuded electrical energy and thermal
energy in reacting transformation of an atomic hydrogen in molecular. Let's
consider, that this energy we have spent for control of a thermal mode of the
installation, since it very much resembles a nuclear reactor and potentially is
capable to result in potent thermal explosion. In 100 l are contained
100:22.4=4.5 mols of gas, or 4.5×6×1023×2 = 0.54×1025 atoms. At each interplay of a
proton with an electron with formation of normal atom of hydrogen is excreted
13.6 eV of energy. The general energy release in this process will make 13.6×0.54×1025 eV or
quantity of energy to equivalent incineration of 280 liters of gasoline (and
weight of hydrogen in a vessel only 9 grams). Thus, the power accumulator will convert
«gigantic» hydrogen in ordinary in ecological clean process. Naturally, that
the obtained energy at a plant on production gigantic atoms should be expended.
In a pressurized vessel charged by gigantic moleculas of hydrogen at
large pressure under operating of an electric spark there is an instantaneous
transformation of gigantic hydrogen in normal to such energy release, which one
is unapproachable at usage of any known explosives.
Basically, any gigantic atoms can be used for welding, knife cut and
meltings of any materials, including, and in space conditions also.
21.3. Energy balance at
change of a satellite orbit
This chapter is written with the purpose to help to the readers clearer
to understand, that occurs at attempt to change orbit of a satellite.
From equality of attractive force of a satellite to a central body and
centrifugal effort for any equilibrium circular orbit the formula is fair:
(21.3.1),
where: V - orbital velocity, G - gravitational constant, M
- mass of a central body, r - radius of orbit.
Let's multiply both parts (21.3.1) on m/2, where m - mass
of a satellite:
(21.3.2).
The left-hand part of an equation (21.3.2) represents potential energy
of a universal repulsion (chapter 1), therefore it is convenient to record
(21.3.2) for a low-altitude orbit 1 and high-altitude orbit 2 and
to find a difference of universal energy of a repulsion Erep
for these orbits:
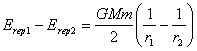(21.3.3).
The equation (21.3.3) demonstrates, that the difference in energies of a
repulsion for two orbits makes equally half of difference of attraction energy
to a central body. On a virial theorem for a steady dynamic system the
potential energy of attraction is peer to the sum of potential energy of a
repulsion and same bond energy. Therefore, second half of change of energy of
attraction in (21.3.3) is spent for change of bond energy of a satellite with a
central body. At transition of a satellite from a low-altitude orbit on high
«kinetic» energy of a satellite (energy of a universal repulsion)
proportionally decreases, the bond energy it with a central body and potential
energy of attraction to a central body decreases. The energy conservation law
demands, that these losses should be completely balanced by the makeweight of
«kinetic» energy to a satellite for transfer it on more high-altitude orbit.
Here there is an apparent paradox: We should speed up a satellite to reduce its
orbital velocity on more high-altitude orbit. Thus the expended energy not only
completely is compensatived, but also the part will be used at the expense of
initial speed. For transfer of a satellite from a high-altitude orbit on lower
it is necessary to make the conforming inhibition and again there is an
apparent paradox: we have reduced an orbital velocity, and it, in the total,
was increased on a low-altitude orbit.
Here it is necessary to add rectification. At attachment of speed to a
satellite on orbit 1, it starts to move on elliptical orbit with
pericentre in a point of the added speed, having exuberant energy. At motion
from pericentre to an apofocus of orbit change of energy will correspond
above-stated. If we want, that orbit 2 satellites should have become
circumferential, we need to add in a point of an apofocus such speed, that it
completely corresponded to the formula (21.3.1).