COLLOID SYSTEMS

1. KINETIC EQUATION of COAGULATION

The particles of colloids and suspensions in relation to molecules are macroobjects, and in matching with customary macroobjects have the microscopic sizes, i.e. take an intermediate standing in scale hierarchy. At the same time they have the particular properties, usage which one is important for a biology and technology. All living organisms as a matter of fact represent colloid systems.

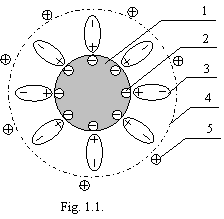
I shall remind, as the colloid particle (or larger particle of suspension), shown on a figure 1.1 is arranged.

On a figure 1.1: 1 - colloid particle, 2 – potentialdefining ions, adsorbed on a surface of a particle, 3 - solvate layer of oriented dipoles (molecules of water) thick several hundreds molecules, 4 - sliding surface in a disperse medium, 5 - counterions.

At a Brownian motion of a particle, if it is not enough of counterions, they have no time compensate electric charge of potentialdefining ions, therefore particle has some electric potential  (zeta-potential). The zeta-potential stipulates stability to sticking (coagulation) of colloid particles. If in a disperse medium there will be a sufficient amount of counterions, - potential is reduced and there is a coagulation. The colloid particles stick together among themselves, but the electric charge them thus practically does not vary, because of what they can not form uniform large aggregate. Therefore in the kinetic equation Smoluhovsky it is necessary to allow for equilibrium calculating concentration of aggregates . The value  is bound, on the one hand, to a coulomb repulsion of particles component aggregate, on the other hand, this value depends on an adhesive strength of particles in aggregate, which one depends on a state of a solvate layer.

Accepting, on Smoluhovsky, the second order for a kinetics of sticking of particles taking into account of equilibrium calculating concentration, it is possible to record:

                                        (1.1.),

where C - current concentration of particles, 1/cm³.

The solution of the equation (1.1.) it is possible to present as follows:

                                  (1.2.),

where C₀ - initial calculating concentration of particles, 1/cm³, K - constant of velocity of a coagulation, cm³/sec.

The kinetic equation of Smoluhovsky:

                                          (1.3.)

is a particular case of the equation (1.2.) at =0. The equation of Smoluhovsky displays the rather good consent with experiment only in an initial stage of coagulation. In further decrease of concentration of particles goes slower, than on the equation (1.3.).

At use by the equation (1.2.) there is a problem of definition of an equilibrium concentration of aggregates. For deep stages of process C comes nearer to  and the processing accuracy of an experimental curve strongly depends on an error of definition . If concentration C₀ to accept for unity, then C and  will be expressed in shares of unity and the equilibrium concentration can be determined from coordinates of two experimental points (₁, C₁) and (₂, C₂) on the equation:

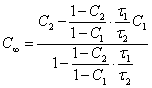                                    (1.4.),

which one is received from (1.2.). By multiplication of the retrieved value  on C₀ and substitution in (1.2.) let's receive value constant of coagulation velocity. If the equation (1.2.) to converse to a view:

                                  (1.5.),

that more precise value of a constant of velocity can be found from tangent of a slope angle straight line in coordinates: - time.

Would be insecure to search for an activation energy of a coagulation process on dependence the retrieved constant of velocity on temperature of process, since decrease of viscosity with temperature rise in this case is not consider, that will give obtained value of an activation energy above real.

On Smoluhovsky, the constant of velocity of coagulation is determined by expression:

                                        (1.6.),

where: k – constant of Boltzmann, erg/deg,

T – Kelvin temperature, deg,

 - viscosity of a colloidal solution, dyne×sec/cm²,

W – probability of effective collision of particles.

Here it is necessary to mark, that at a prompt coagulation the value W can appear more unity at the expense of an attraction of colloid particles, in spite of the fact that they is of the same name are charged. This attraction is stipulated by mutual reorganization of exterior solvate layers of approaching particles.

By determined experimental value of a constant of velocity, from (1.6.) it is possible to find W. On dependence W on temperature of process we shall discover activation energy of coagulation from the equation:

                                 (1.7.),

where E - activation energy, erg/g-mole. As the value E during coagulation is insignificant, it is better to take advantage of the equation, more approaching for this case, (Y.I. Gerasimov etc. Course of physical chemistry. v. 2, М., 1966, page 129-130):

                             (1.8.).

Calculation on (1.7.) or (1.8.) automatically allows for change of viscosity of a colloidal solution with temperature and consequently allows finding more precise value of activation energy of process. Here it is necessary to specify, that the activation energy of coagulation has the relation only to strength of a friable outside of a solvate layer of colloid particles. The interior parts of a solvate layer are so strong, that their reorganization and gradual obturating of aggregates can happen within several years. From this fact it is possible to draw a conclusion, that the activation energy of reorganization of a solvate layer is incremented sharply as penetration in it that indicates its special strength near to a surface of a colloid particle.

Immediate experimental check-up of the kinetic equation (1.2.) is possible with the help of a stream ultramicroscope. I have processed major number of literary data on kinetics of coagulation. If the diversion from the equation of Smoluhovsky in case of a sluggish coagulation does not call doubts, for a prompt coagulation this equation, is customary consider valid, though the kinetics was studied only in a start of process. However, it is necessary to mark, what even in a case of «super prompt» coagulation, when W>1 and the colloid particles are attracted to each other, all they have -potential nonzero. It gives that as accumulation of particles in aggregate the electrostatic barrier is incremented for sticking the subsequent particles. Besides because of a Brownian motion or gradient of velocities of a dispersion medium the friable large aggregate ruins. Thus, and in this case we shall have though also small, but quite sizable value C_¥. For an example, on a figure 1.2. the results of calculation of a prompt coagulation of sol of gold on data (G.R. Kroit. Science about colloids. FL, М., 1955) are given. C_¥, retrieved from (1.4.) equally 0.028×C₀. A curve 1 - on the equation of Smoluhovsky, straight line 2 - on the tendered equation (1.2.).

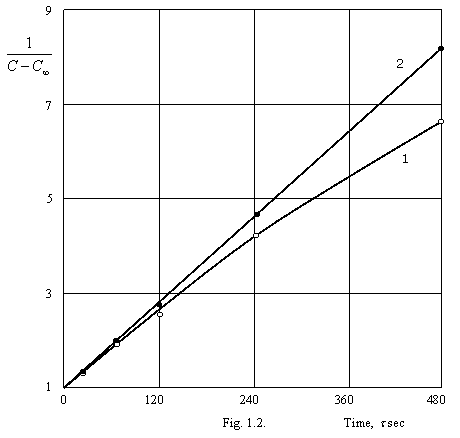From a figure 1.2. it is visible, that the kinetic equation of Smoluhovsky does not approach for given system, since it is impossible straight lines at =0. At the same time, equation (1.2.) well describes a viewed case of coagulation given in the literature confirming a regularity of the equation Smoluhovsky. The constant of velocity retrieved from a slope angle received straight line has appeared equal 7.38×10^-12 cm³/sec. This value, apparently, a little is overstated, since the intermixing of a colloidal solution at applying a stream ultramicroscope is inevitably. In the following chapter the method investigation of a kinetic of coagulation free from it and other deficiencies will be offered. Probability of effective collision of particles from (1.6.) is peer 1.38 that indicates a prompt coagulation.

Thus, the improvement of the equation Smoluhovsky, well-handled by us, allows considerably extending area of its applying.

2. OPTICAL METHOD STUDY of COAGULATION KINETICS

The tendered below optical method study of coagulation kinetics will be useful specially to medicine, since has an exclusive simplicity, precision and sensitivity. It will allow with a fast response on a kinetic of coagulation of blood elements to determine pathology, poisons and other substances in an organism.

The method of study of kinetics of coagulation by means of a stream ultramicroscopy can not be widely inserted in laboratory practice on two circumstances. First consists of influence of intermixing of a colloidal solution, inevitable in a stream ultramicroscopy, on kinetics of process. The second difficulty is bound to complexity of the relevant equipment and complexity of experiment. These circumstances have forced me the equation, obtained in the previous chapter, to modify so that it was possible to apply to experimental data of change of an optical behaviour of colloid systems obtained on a photocolorimeter. The record of change of an optical density of colloid system is becomes by a recorder. To avoid intermixing a solution and to avoid influence of sedimentation of aggregates, process carry on in hermetically closed down temperature-controlled to a basin without bubbles of air in it. Basin it is slowly (2 rev/min) is gyrated, thus the aggregates, generator in colloid system, at the expense of a sedimentation circumscribes circles of very small diameter in matching with a diameter of a light ray reading an optical density. Thus, the experiments on coagulation are fully automated and they are not influenced by strange actions.

2.1. Large colloid particles (suspensions).

If the size of colloid particles is more than 1/3 wave lengths of a light radiation (suspensions), under the theory Mi, the particle in aggregate exhibits the individuality and appears as simple scattering centre. If the size of a particle is less than 1/4 wave lengths of a light radiation (colloids) individuality of a separate particle is lost and, as the simple scattering centre, appears already aggregate. For such particles the theory of the Rayleigh is valid.

Viewing three cases is of interest: a coagulation in chains, planes and volumetric aggregates, since all these views of structures can be obtained both on model, and on technological systems.

For a case of aggregation in chains the current optical density will be proportional 2N+1, where N - number of particles in aggregate, since from a requirement of an equality probability standing of aggregates, the device will be «to see» from each three aggregates two aggregate with number of the particles N and one aggregate with number of particles to equal unity (with «of a back»). The initial optical density is proportional to total of particles in these three aggregates, equal 3N. Thus, from the ratio of an initial optical density to current, we shall discover for linear aggregates:

                                     (2.1.1.).

Similarly reasoning, we shall discover for flat and volumetric aggregates, accordingly:

                                    (2.1.2.),

                                           (2.1.3.).

On the other hand, apparently, that number of particles in aggregate in any case:

                                           (2.1.4.),

where: C₀ - initial calculating concentration of particles, 1/cm³,

C - Current calculating concentration of particles, 1/cm³.

By substituting (2.1.4.) in (2.1.1.), (2.1.2.) and (2.1.3.), we shall receive connection between calculating concentration of particles and optical density of suspension at formation of linear, flat and volumetric aggregates accordingly:

                                     (2.1.5.),

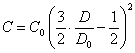                                 (2.1.6.),

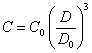                                     (2.1.7.).

View of the equations (2.1.5.), (2.1.6.) and (2.1.7.), as it is visible from previous, does not depend on a packing density of particles in aggregates. From them also it is visible, that the process of coagulation in a viewed case of large colloid particles (suspensions) gives in diminution of an optical density of suspension.

Substituting the obtained equations in (1.2.) the previous chapter, after some transformations, we shall discover for linear aggregates:

                          (2.1.8.),

for flat aggregates:

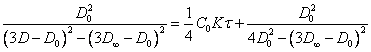       (2.1.9.)

and for volumetric aggregates:

                           (2.1.10.).

The equations (2.1.8.), (2.1.9.) and (2.1.10.) give straight lines in coordinates, on an axis of ordinates which one the values of the left-hand part of the equations, and on an abscissa axis - time are measured off.

The quantity  can be retrieved from coordinates of any three experimental points (₁, D₁), (₂, D₂), (₃, D₃) on the equation:

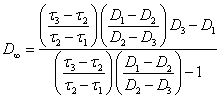                      (2.1.11.)

for linear aggregates. For volumetric aggregates:

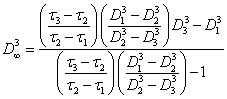                    (2.1.12.).

The equations (2.1.11.) and (2.1.12.) though and bulky, but are friend for practical calculations. The expression for  in case of flat aggregates is more complicated:

              (2.1.13.),

where:

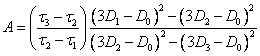              (2.1.14.).

For equidistant values  equations (2.1.11.), (2.1.12.) and (2.1.13.) are considerably simplified.

Thus, utilizing the equations (2.1.8.), (2.1.9.) and (2.1.10.) together with expressions (2.1.11.), (2.1.12.) and (2.1.13.) for  it is easy to find from measurements an optical density a constant of velocity of a coagulation of suspension and, therefore, efficiency of particles collision.

2.2. Colloid systems from small particles.

The small particles collected in aggregate do not exhibit optically individuality and the aggregate as a whole appears as one scattering centre. This statement is valid for particles of smaller 1/4 wave lengths of a light radiation, i.e. arranged more to the left of a dispersion maximum, under the theory Mi.

On the Rayleigh (G.R. Kroit. Science about colloids. FL, М., 1955, page 413) the optical density of a colloid is proportional to a quadrate of volume of a particle, scattering light:

                                           (2.2.1.),

where: k - coefficient of proportionality, 1/cm³,

C - concentration of particles in a unit volume, 1/cm³.

Noting the ratio of a current optical density to initial, we shall receive:

                                          (2.2.2.).

Weight of aggregate, formed to the instant :

                                   (2.2.3.),

where: r₀ - radius of a particle, cm,

r - radius of aggregate, cm,

N - number of particles in aggregate,

 - density of a particle, g/cm³,

¢ - density of aggregate, g/cm³.

From (2.2.3.), allowing, that N=C₀/C and designating ¢ /=, where  - packing density, in a limit varying from 0 up to 1, we shall discover:

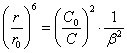                                   (2.2.4.).

By substituting (2.2.4.) in (2.2.2.), we shall receive:

                                     (2.2.5.).

From the equation (2.2.5.) it is visible, that as against large particles of suspensions, the coagulation of small particles of colloids gives in magnification of an optical density of sol.

By substituting (2.2.5.) in (1.2.), we shall receive the equation of coagulation kinetics of sol expressed through an optical density:

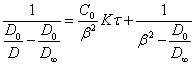                         (2.2.6.).

The equation (2.2.6.) gives a straight line in coordinates: 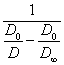- time, constant of coagulation velocity whence can be retrieved. The quantity  imports some indeterminacy to a true value of a velocity constant.

The value  can be retrieved on coordinates of three experimental points (₁, D₁), (₂, D₂) and (₃, D₃) from the equation:

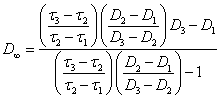                       (2.2.7.).

Thus, using results of chapters 2.1. and 2.2. the study of a coagulation of suspensions and sols in all a range of the sizes of particles relevant selection of a wave length of light is possible, at which one will carry out measurements an optical density.

Our experiments with a coagulation of suspensions (TiO₂) and sols (AgJ) have shown, that the equilibrium size of aggregates depending on concentration of an electrolyte at a threshold of a coagulation reaches the maximal sizes, and the course of change  represents practically precise differential velocity curve of a coagulation.

3. CONNECTION BETWEEN ZETA-POTENTIAL And ION ACTIVITY In DOUBLE ELECTRICAL LAYER.

In the literature there are quantitative evaluations of change of properties of a solution, for example values pH near to colloid particles. At the same time this index in basic determines destiny of a hydrolysis of solutions and adsorption of impurities on hydrolysates. In this connection there is a necessity of a quantitative evaluation of ion activity of electrolytes near to colloid particles.

As have shown our experiments with a hydrolysis of sulphate titanium, depending on conditions deriving a metatitanic acid both in coagulated state, and as sol with positive -potential is possible. The high stability of such sol to aggregation can not be explained by a repulsion of particles at overlapping double diffuse electrical layers of crystallites of a metatitanic acid because of high concentration of electrolytes in a mother solution. The more probable reason of a stability is the presence of a solvate layer environmental a particles of a metatitanic acid and at it so strong, that the ions, adsorbed from a solution, place on its surface and the allocation of ions around of a colloid particle is represented by a lamina on a surface of its solvate environment.

The deduction of the basic equation linking ion activity on a surface of a solvate layer to activity them in a mother solution and -potential of colloid particles is founded on definition of concentration potential (N.A. Izmailov. An electrochemistry of solutions. М., 1966, page 467):

                                            (3.1.)

and discussion of the mechanism of adsorption of ions in view of a principle of detail equilibrium.

For definiteness, assume, that the colloid particle is charged positively and potentialdefining ions strongly chemisorbed by a surface of a particle and are not capable to an exchange. Let's designate potential of a colloid particle without counterions through . We suppose that at adsorption of ions potential of such particle is reduced on quantity, defined concentration potential of a given sort of cations and anions. Assume, that the particle is in water not containing of electrolytes. Then counterions will be ions of hydroxyl, and the blanket change of potential of a particle will make:

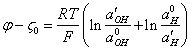                             (3.2.),

where: ,  and , - activity, accordingly, hydroxyl and proton on a surface of a solvate layer and in a solution, g-mole /l,

F - Faraday constant, coulomb/g-mole,

- zeta - potential of a colloid particle in absence of an electrolyte, v.

Let's discover connection between activities of a cation and anion in an equilibrium diffuse double electrical layer, then from a principle of detail equilibrium follows, that in the same relation cations and the anions will be sorbed and on a surface of a solvate layer of colloid particles.

From equilibrium condition of forces for a given cation in a diffuse double electrical stratum follows:

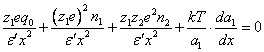                  (3.3.),

where: e - elementary charge, units CGSE,

q₀ - charge of a particle without counterions, units CGSE,

    n₁, n₂ - number of cations and anions in a double electrical layer inside a sphere, on a surface by which one is a given cation,

¢ - dielectric constant of medium in a double electrical layer,

x - distance from centre of a particle up to a given cation, cm,

        z₁ and z₂ - valence, accordingly, cation and anion.

In the equation (3.3.) the terms sequentially correspond: to an attractive force of a cation to a particle, repulsive force from like ions, attractive force to ions of an opposite sign and «diffuse» force relevant to a repulsion from a particle.

Noting similar expression for an anion and substituting n₂ from it in (3.3.), we shall receive the differential equation linking of activity of a cation and an anion in a double electrical layer. The solution of this equation following:

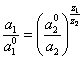                                         (3.4.).

Charges of a cation and anion in the equation (3.4.) are taken on an absolute value. This equation will be valid and for a flat double electrical layer, since a view of the first three members of equation (3.3.) does not influence the solution.

Substituting (3.4.) in (3.2.), we shall receive:

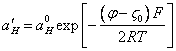                              (3.5.).

Potential  for the majority of sols makes about 0.2-0.3 v, and  about 0.1 v. Then of the equation (3.5.) follows, that pH near a particle of refined negatively charged hydrosol, approximately, on 2 unities it is less, than in a solution at pH~7.

The obtained result completely coincides experimental data (Harter Robert D., Anlrichs James L. Soil Sci. Soc. America Proc., 31, 30, #1, 1967), which one have found, that on a surface of bentonitic clay pH on 2 unities it is less, than in a solution at pH~7.

For a case, when at a solution there is an electrolyte and  up to value  is reduced, similar (3.2.) it is possible to note:

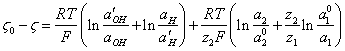        (3.6.),

where: ,  and ,  - activities, accordingly, hydroxyl and anion, proton and cation on a surface of a solvate layer, g-mole/l,

 and  - activities, accordingly, anion and cation in a solution, g-mole/l.

From (3.6.), utilizing (3.4.), we shall discover:

                             (3.7.).

The equation (3.7.) with the registration (3.5.) it is easy to converse to a view, friend for counting pH near positively of charged colloid particles:

                          (3.8.),

where: pH₀ - value pH in a mother solution.

For negative of charged colloid particles signs of two last members of equation (3.8.) it is necessary to change on opposite.

The physical sense of obtained expression consists in dependence of adsorption of hydrogen ions on a surface of a solvate layer of colloid particles from presence in a solution of other ions.

Substituting (3.7.) in (3.6.), we shall discover activity of counterions on a surface of a solvate layer for positively or negatively of charged colloid particles:

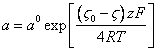                                   (3.9.),

where: z - valence of a counterion.

4. ADSORPTION of IMPURITIES ON a SOLVATE LAYER of PARTICLES AND STABILITY CRITERION of COLLOID SYSTEMS.

The numerous experiments with all evidence display, that the aggregate stability of colloid systems is determined by presence of a strong solvate layer environmental a colloid particles. All our attempts to explain the test data from stands alone now to quantitative stability theory of colloids DLFO invariably conflicted to experiment. In a basis of this theory two basic interactions are included: Van der Waals an attraction and repulsion at overlapping diffuse layers of counterions of colloid particles. In technological systems as against model laboratory systems there are both factors absent. First - because of presence of a thick solvate layer superior on the sizes a radius of action of Van der Waals forces, second - because of high concentration of electrolytes.

In work (G.A. Martinov, V.P. Smilga. The colloid journal, 27, 250, 1965) was shown, that the particles boarded with dipoles will be attracted. Such deduction is grounded on high mobility of polar molecules on outside boundary of a solvate layer. However, in my opinion, the sign of interaction depends on amount of counterions adsorbed on a surface of a solvate layer. If it is not enough of counterions, the dipoles on a surface of a solvate layer have no time to be turned during collision of colloid particles and between them the repulsion is watched. If it is enough of counterions for loosening to an outside surface in such degree, that it is possible to consider dipoles practically as free, the repulsion is replaced by an attraction according to the above-stated reference. The particles in this case will formed aggregate as a result of touch of solvate envelopes.

Derivation of an equation linking adsorption of ions on a surface of a solvate layers of colloid particles to an activity coefficient them in a solution given below. On the basis of this equation the stability criterion of colloid systems is obtained, the stability which one is bound to presence of a solvate layer.

Adsorption rate of counterions on a surface of a solvate layer:

                                            (4.1.),

where: K₁ - constant of an adsorption rate, cm²/sec,

₁ - surface density of counterions in a dispersion medium, 1/cm².

Velocity of desorption of counterions from a surface of a solvate layer in a dispersion medium:

                                           (4.2.),

where: K₂ - constant of velocity of a desorption, cm²/sec,

₂ - surface density of counterions on a solvate layer, 1/cm².

As the factors impeding installation of equilibrium in a considered case miss, the equilibrium is established rather promptly:

                                         (4.3.).

Substituting in (4.3.) the equation of the Arrhenius:

                                    (4.4.)

and apparent relation between ₁ and concentration of counterions in volume of a colloidal solution:

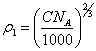                                        (4.5.),

let's discover:

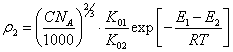                        (4.6.).

For an activation energy of a desorption, as a first approximation, omitting interaction with a solvate layer, we shall accept an electrostatic energy interaction of a counterion which is taking place on a surface of a solvate layer, with a charged colloid particle:

                                    (4.7.),

where: q - charge of a colloid particle, unit CGSE,

z - valence of a counterion,

 - distance from centre of a colloid particle up to an outside surface of a solvate layer, cm,

¢ - medial effective dielectric constant of a solvate layer (it is diminished as approaching a surface of a particle).

The equation (4.7.) without damage to a further deduction it is possible to exchange by an apparent and more blanket relation: E₂=E₂(₂).

Energy of activation of adsorption is peer a viewed case to exuberant work of transport of a counterion from volume of a colloidal solution on a surface of a solvate layer. This work is peer to the total of exuberant work on transport of a counterion from a given solution in indefinitely a weak solution (N.A. Izmailov. An electrochemistry of solutions. М., 1966, page 53):

                                            (4.8.),

where * - concentration activity coefficient of a counterion and exuberant work on transport of an ion from a dispersion medium (free dipoles) on a surface of a solvate layer (bound dipoles):

                                           (4.9.),

where ₀ - uniform zero activity coefficient of counterions.

Thus, the aggregate exuberant work of transport of a counterion will be:

                                         (4.10.),

where:

                                               (4.11.).

By substituting the equations (4.7.) and (4.10.) in (4.6.), we shall receive the basic transcendental equation:

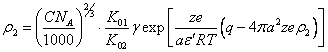               (4.12.).

From the equation (4.12.), as the special case, is possible to find a requirement, at which one density of counterions on a surface of a solvate layer is peak, and, therefore, the efficiency of a concussion of particles is peak, as the quantity of the liberated dipoles on a surface of a solvate layer is proportional to quantity of adsorbed counterions.

From here, for a threshold of a coagulation it is possible to note a requirement:

                                           (4.13.).

The equation (4.12.) under condition of (4.13.) to become:

                                        (4.14.).

By accepting dependence between lng and C under the theory of a Debye-Hukkel (N.A. Izmailov. An electrochemistry of solutions. М., 1966, page 106):

                                         (4.15.)

and by substituting it in (4.14.), we shall discover a requirement for a threshold of a coagulation:

;      =0,263                                 (4.16.).

The equation (4.16.) it is necessary to view as a stability criterion of colloid systems. The result obtained in this equation does not depend on a view of the equation (4.7.).

By taking advantage a stability criterion (4.16.) it is possible to find a stability criterion of hydrosols. For this purpose it is necessary to determine value of a dielectric constant on a surface of a hydrated layer of colloid particles.

On data of many researchers the thickness of a solvate layer oscillates from 100 up to 2000 angstrom units. The majority of the researchers give for a hydrated layer numeral about 350-400 Å. The dielectric constant of water varies depending on thickness of a film from 4.5 at thickness 70 Å up to 75 at thickness 1600 Å, the value for free water 80 is reached at thickness of a film 37000 Å. At interpolation of these data to thickness of a film in 350-400 Å there corresponds a dielectric constant of water about 40. Then, accepting quantity of a dielectric constant equal 40 on a surface of a hydrated layer that corresponds to «half-bound» dipoles of water, from the appendix to the monograph (N.A. Izmailov. An electrochemistry of solutions. М., 1966) we shall discover approximate experimental value : lg0.45, 2.82. After substitution (4.16.) in (4.11.), we shall receive at a threshold of a coagulation of hydrosols:

                                 (4.17.).

If to substitute (4.17.) in the equation of a Debye-Hukkel for an activity coefficient of ions, we shall receive expression for concentration of an electrolyte at a threshold of a coagulation.

The equation (4.17.) known empirical regularity detected by Oswald on hundreds of experiments and a corollary from it explicitly are argued in his work (V. Oswald. Successes of chemistry, 9, #5, 1940). It is possible to term as a stability criterion, defined equation (4.16.) generalized rule of Oswald. This criterion allows both property of a dispersion medium, and property of a solvate layer of colloid particles and, therefore, is bound to properties of matter of these particles. Allowing expression (4.10.), it is possible to formulate this criterion in a little bit diverse view: the colloid system will have a minimum stability to aggregation, when the activation energy of adsorption of counterions on third is more than their thermal energy.

In that specific case of lyophobic sols the obtained stability criterion transfers in a rule of Oswald. For example, studying a coagulation of sols of sulfur (S.E. Harin, I.V. Chaikovskay. A colloid journal. 18, 350, № 3, 1956) writers have found affirming to a rule Oswald: *=const=0.73.

Физический смысл этого результата состоит в том, что при малой концентрации электролита ионы сильней удерживаются на поверхности адсорбента, чем в растворе, а при большой концентрации взаимодействие ионов с раствором сильней, чем с адсорбентом. View of a relation (4. 16.) displays, that it can be applied to a general case of adsorption of ions from solutions of electrolytes on a surface of an adsorbent, when the activation energy of a desorption is some function from quantity of adsorbed ions (that almost always has a place). In this general case we shall receive the same result: the maximum of adsorption is watched at ln=-4/3, where =*/₀. The physical sense of this result is, that at small concentration of an electrolyte the ions are retained stronger on surface of an adsorbent, than in a solution, and at major concentration the interaction of ions with a solution is stronger, than with an adsorbent.

5. MAGNETIC PROCESSING of WATER

The first information about influence of magnets to properties of water go from medicine, since XIII centuries (Geneva physicist de Gersu). The most classified information are obtained since the 30-th years XX centuries Dgordgio Pikkardi, which one on the basis more than 250 thousand observations has installed statistically reliable connection between activity of the Sun and rate of sedimentation in water of sol of an oxychloride of a bismuth (gained by a hydrolysis, of a trichloride bismuth). In 1945 the Belgian engineer T. Vermaer has licensed a method of strife with a scale deposit by means of magnetic processing of water containing hardness salts. This method - one of the most reproduced and effective practical appendices of magnetic processing, therefore it is fullestly learnt. In a basis of effect improvement requirements of dropout of crystals of hardness salts from heated water not on solid walls, and in water volume. Thus in 5 times the number chips is incremented and in as much time their size is diminished. The size, certainly, can not decrease in as much time, in how many of time the number of chips was increased, a deficit of total mass of allocated chips differently will appear, so the thermodynamic equilibrium of response will vary, that is improbable. This inconsistency is possible will be removed by that after magnetic processing from water fall out the chips not of a calcite, and aragonite (on data A.M Krapivina etc.). In this case estimation of a regularity of data is not so relevant, since the sufficient quantity of contradictory experimental data will below be given. In most cases good results are gained, if the water concerns to a calcium-carbonaceous class.

After discovery of Vermaer of starts indeed "magnetic boom" in medium "applyers". The practical results have not slowed to have an effect, but at the same time idea of magnetic processing of water discredited itself in ever more to eyes of the scientists, as in absence of scientific explanation of apparent effects in the literature occurred contradictory from a scientific point of view experimental data. Now business has reached that everyone can receive by means of magnetic processing that him is necessary. I shall give some examples.

1. Frequently already after contact before a having been available scale deposit with magnetized water the scale deposit starts to be dissolved and to fall off walls, and on data of Tatarinov the magnetic processing accelerates dissolution in 5 times, and on data of Scorobogatov the velocity of dissolution MgS0₄ is incremented in 120 times. It contradicts above mentioned data from which one follows, that the magnetic processing promotes not magnification, and diminution of a dissolubility of hardness salts. Escaping of mentioned inconsistency, apparently, in poor "purity" of experiments concerning absorption by system in a run time of extraneous gass (in this case CO₂). So for example, the merging of a solution of nitrate lead with a solution of caustic potassium gives in formation of lead hydroxide, and after magnetization of lead salt - to formation of lead carbonates because of increase concentration СО₂ in a solution. The truth, is not known, it is possible the writers in the second case took "old" caustic potassium, which one, as is known, absorbs CO₂ from air with formation of potash. At the same time there are independent data (Korukin, Klassen) about magnification of the content of oxygen and carbon dioxide in processed water, for example, because of magnification of concentration O₂ in magnetized water, the oxidation rate of pyrite FeS₂ in water will increase on 20%. However, dissolubility of gases, as the quantity thermodynamic should not vary and consequently the indicated effects should be viewed as magnification of velocity of dissolution of gases in processed water. Then it is possible to draw a conclusion, that magnetized water in itself accelerates dissolution of matters including gases, and the diminution of a dissolubility of hardness salts is bound to influence of the enlarged content СО₂ in waters processed for preventing of a scale deposit.

2. It is discovered, that the wetting power of water after processing is diminished. But for surfaces containing silicon it is incremented. By Klassen sets, that dedusting ability (rock dust and the coal) processed water in 3 times is higher, that contradicts him data on aggravation of a wetting power of processed water. At water injection in a seam of coal it is spread there almost twice further, i.e. the wetting power of water is meliorated. From this inconsistency yet it is not visible of an exit. 

3. Grebnev, Klassen etc. have ascertained that the magnetic processing heightens velocity adsorptions of surface-active substances on solid surfaces and on partition water - air. Soloshenkin etc. have ascertained that the adsorption of dyestuffs on a fibre is incremented by 42 %, and Tatarnikov etc. have found, that magnetized water on 40 % accelerates washing out of a fiber from dimethylformamide. Liakumovich considers, that magnetized water washes materials from impurities better. Too unsolvable experimental inconsistency.

I shall give still brief examples showing as knotty problem in result of which experimenters is "reach" that to what tend, solving, frequently, opposite problems by the same expedient.                                           

At extraction of watered oil in tubes put magnets, in result the deposition of salts is diminished at 6-12 of time, and the old depositions fail. At tempering cement by magnetized water the strength it is incremented, more fine grained structure in 2.5 times is gained the gas permeability of a cement rock is diminished.

The processing increases strength of the sandy-argillaceous shapes for a casting and simultaneously increments their gas permeability.

The processing of water on which one gets mixed up mass for molding of a brick increments its strength and reduces porosity.

The processing of pulp at floatation increments extraction of copper and gold, sorptive capacity of ion exchangers is incremented, on 20-30% will increase capacity absorption of sulfonated coal.

Verishskay has found, that the velocity of interaction of acids with metals will increase approximately in 2 times after processing, but at some magnetic intensity the interaction is retarded sharply.

By production of caustic the degree of causticization is incremented by 6 %.

The unit discharge of diamonds is reduced in 3 times at grinding; the stability of oil-water emulsion is many times over incremented.

Skalozubov, Kukoz and Chernov have found even, that by production of soda salt in 2 times the equilibrium constant varies with diminution in 2 times of concentration of soda salt in the clarified solution, that generally is difficult for believe, since it contradicts thermodynamics.

The necessity of eduction of the rather reliable test data and prime for the analysis of systems streams from viewing all now obtained by experimental "kasha":       

1. The magnetic processing promotes dissolution in water of carbon dioxide and oxygen, picks up speed dissolutions of matters.

2. The processed water biologically is active.

3. The coagulative processes are accelerated.

In the second case the system is so complicated, that it is necessary to draw a conclusion only that the magnetized water by something differs from customary.

Let's transfer to a problem on what requirements are indispensable for development of effect. Thus also we shall reject all some doubtful or single data.

1. Presence of impurities.

For water alone the effects are not watched. Generally change of properties of water after magnetic processing will increase with magnification of an impurity concentration in some limits. The major role is played by character of impurities. Duhanin has come to a deduction, that the information is born with water, and the ions boost or attenuate shown effect. A blanket deduction on 1 point while we shall make such: or the properties of water on themselves vary, and the ions as determine that these changes, or these changes of water are possible only at presence of ions, or the water is nothing play a role only ions.

2. Stream of processing system in a magnetic field. 

If no travel concerning a field effect is not watched. At stream arise only of Lorentz forces. A blanket deduction on 2 point. The activity is exhibited only in those systems, where can arise of Lorentz forces (dipoles, ions, charged colloid particles etc.).

3. Speed of flow.

For development of effect in full measure optimum rate of flow is necessary. With magnification of velocity the effect is incremented and then falls. This point is very relevant on the informative value, since displays, that for development of effect the rather major run time of processing is necessary. The deduction of the first point remains only in edition Duhanin, as it is known, that the chemical reactions between ions in a solution go practically instantaneously. But here it is necessary to add, that macro transference of ions under activity of Lorentz forces requiring of a long time can not also give a curve with a maximum. From a deduction of the 2 point there is an activity of Lorentz forces on dipoles of water (for a pure solution) and ions in the sense that they can as influence behaviour of dipoles.

4. Frequency of change of a field.

Low-frequency processing strongly operates on water: unities or tens hertz (it just corresponds to a stream with velocity of 1 m/s in a backlash of length 10 cm). The deduction till item 4 same, as till item 3: for formation омагниченной of magnetized water is necessary time.

5. Field strength.

The effect of processing in dependence from a field strength is in polyextreme dependence and, at all events, nonmonotone. On the one hand, it could be explained to that during processing there is, at any rate, one interfering factor. On the other hand, the coagulative processes, for example, not monotonically depend on concentration of a coagulable electrolyte. Let's remind that the reliable effect of activity of a magnetic field is by and large bound to coagulative processes in processing system.             

6. Relaxation time.

The spontaneous returning of aqueous systems after magnetic processing in a reset state takes on time a gamut from several tens minutes about several day on data of the miscellaneous writers. The magnification of temperature accelerates process of a relaxation. From here it is possible to draw a conclusion, that called in the control system thermodynamically are not stable, but the process of a relaxation meets considerable kinetic handicappings.                                            

As the theory of a phenomenon is not present, we shall transfer to viewing present now hypotheses, the deficiency of which one is not present.

1. "Colloid" hypotheses. In their basis the activity of a magnetic field on colloid particles possessing a rather major magnetizability (a para- or ferromagnetic) and always lies present in water. Therefore water alone not magnetization.     

Against this kind of hypotheses speaks that fact, that the magnetized water gradually loses the properties, i.e. the effect reversible, at the same time, the colloid processes are nonreversible.

2. "Ionic" hypotheses in which one the basic liability is laid on ions taking place in water. In a basis the activity of a magnetic field on moving ions lies. The majority of the supporters underline a major role of influence of a magnetic field on a hydration of ions (hydration is diminished). In the proof give magnification on 20-40% of sorptive capacity of ionites. By a method NMR (on waist of linewidth of a signal the NMR of water) is shown, that the hydration of ions is diminished after magnetic processing. By the way, the supporter of these hypotheses is Klassen.

Against ionic hypotheses the energy factor, as the energy of a hydration of ions is comparable to potential of ionization of the relevant atoms. At the same time, the energy conferred to water by a magnetic field by intensity 1000 oersteds on 5-6 orders is less than energy of heat motion of water molecules. By the way, it is the basic argument of critics completely negating on its basis any effects at magnetization of water. Imagine house of cards, dying from slightest puff, which one stands calmly at hurricane - approximately so the relation between energy obtained by molecules of water at magnetization and a thermal energy of molecules of water looks.

3. "Water" hypotheses justifying activity of magnetic fields on naturally water. They are grounded on an opportunity of change of properties of water depending on a degree and character of association of its molecules.

For example, Kirgincev has advanced a hypothesis about dispersive activity of a magnetic field on aggregates of molecules of water. The change of aggregate sizes does not call considerable change of a free energy of water, signifies does not require an expenditure of major energy. The mechanism of dispersive activity is not uncovered. Many researchers speak about "structural memory" the water which has visited in a magnetic field.

Unfortunately, the present now hypotheses are so fuzzy, that they cannot be tested in requirements "of major hazard" and, therefore, while it is impossible trusty to confirm or to deny.

Methods of verification of a degree magnetization of water very much indirectly. More or is less lighter for interpretation the aqueous-alcoholic test of Shahov, fixing a degree of diminution of volume of an intermixture of water and alcohol as contrasted to in their individual volumes. Under his testimony magnetization of water volume of an intermixture of water and alcohol considerably diminish. By the way, if this observation is trusty, it indicates such changes, which one are possible only at external pressure on an intermixture in hundred thousand atmospheres.

Hypothesis of the author.

Let's consider now my hypothesis about influence of a magnetic field at aqueous systems.                      

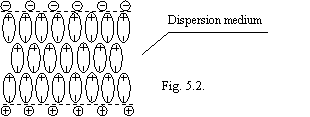
The colloid particles are enclosed by a solvate layer by thick, order 300 Å formed by oriented dipoles of water. This layer will be formed only at presence of a small amount of ions in a dispersion medium, which one, being adsorbed on a surface of a particle, condition for a thermodynamic stability of a solvate layer (potentialdefining ions). The counterions are adsorbed by a lamina on a surface of a solvate layer, which one has such properties, that they do not dive to a surface of a particle. It is possible to judge strength of this layer that at a coagulation (sticking of particles) colloidal solution, the coming together of kerns is prolonged a long time (in some cases months and years). The counterions are arranged by a part in a solvate layer, and part in adjacent to a particle a solution. At a Brownian motion of a particle, the slipping surface lies inside a layer of counterions, therefore particle appears by charged (more often negatively), having some electrokinetic potential. In whole such particle is termed as a micelle. The solvate layer represents "third phase" of colloid system (see figure 5.1.).

In magnetized to water under activity of force of the Lorentz the plate domains of oriented molecules of waters stabilized by ions (of figs 5.2.) will be formed.

Thus it is necessary to mark essential circumstance: the magnetic field not "works", and only instigates formation of these domains, i.e. plays a role of "trigger" (on such role of a magnetic field the academician Vonsovsky indicated). At formation of domains (it is better them to term aquacellas to not confuse to magnetic domains) energy is allotted. After removal of a field aquacellas, as "the third phase" are gradually dissolves, and can be, are aggregated among themselves with descending of counting concentration them.

Let's give some calculations, using the circumscribed model.

1. We compare electrorheological effect to a solvate layer. The colloid particles have z-potential ~ 150 mV, and in a hypothetical case without counterions of the order 300 mV or 0.3 v. Thickness of a solvate layer ~ 300 Å, from here electric intensity at which one the solvate layer becomes thermodynamically stable will make 10⁷ v/m. The electrorheological effect is exhibited at a field strength 10⁶ v/m and has property of saturation at strengths of the order 10⁷ v/m. Thus, the electrorheological effect is called by turn of dipoles in a solvate layer of colloid particles.

2. We shall count up, what there should be a magnetic field to call effect at a level electrorheological.

At electrorheological effect on one double charge of a dipole of water the orienting force 4·10^-15 n, and force of the Lorentz operates at magnetic processing (1 m/s, 1000 oersteds) 3·10^-20 n. Thus, it is necessary in 10⁴-10⁵ times to strengthen a magnetic field to receive effect at a level electrorheological. Completely to simulate structure of a solvate layer a magnetic intensity it is necessary to strengthen in 10⁶ times. Here it is necessary to add, that the solvate layer of colloid particles will be formed in time from several minutes till several o'clock, the time is necessary to maintain system at activity of an exterior magnetic field. Thus the processed aqueous system should "to harden" - the mechanical characteristics of a solvate layer of colloid particles are so high. At electrorheological effect on one double charge of a dipole of water the orienting force 4 · 10^-15 н, and force of the Lorentz operates at magnetic handling (1 m\s. 1000 э) 3 · 10^-20 н. Thus, it is necessary in 10⁴-10⁵ times to strengthen a magnetic field to receive effect at a level electrorheological. Completely to simulate structure of a solvate stratum a magnetic intensity it is necessary to strengthen in 10⁶ times. Here it is necessary to add, that the solvate stratum of colloid particles will be derivated in time from several minutes till several o'clock, the time is necessary to maintain system at activity of an exterior magnetic field. Thus the handled aqueous system should "to harden" - the mechanical characteristics of a solvate stratum of colloid particles are so high.

3. We shall discover energy of formation of a solvate layer from heat of wetting of disperse bodies ~ 60 cal/g. If to accept particles ~ 1 micron, the thickness of a layer 300 Å, is gained ~ 12 kcal/mole. The same energy is allotted and at magnetization of water.                                           

4. We shall estimate concentration aquacellas at usual conditions of magnetic processing, considering, that at processing the magnification of temperature is inconspicuous and is comparable to its magnification from friction at a motion in a magnet gap (~0.1⁰С). 0.01% weight is gained. The actual concentration can be and it is less than that, though the countable concentration of aquacellas, depending from their size can be very major at their small size.

Let's conduct quality estimate of a hypothesis.

1. Presence of impurities.

In a hypothesis the very relevant role is played by ions in water. The completely water alone contains hydrogen ions and hydroxyl in concentration, quite sufficient for development of effect of "memory", but also the ions of impurities, since concentration, order 10^-8 mole/l promote origin of effect. On the other hand, too great many of ions at concentrations about a threshold the coagulation of colloids can, but not always to give in disappearance of "memory". From a hypothesis it is clear, that in absence of impurities the water will be instantaneous to relax at removal of a field. At presence of impurities of a field stabilizing aquacellas all the same remains. In dependence naturally and impurity concentration the effect will be different. 

2. Stream of processing system in a magnetic field. 

This is apparent and indispensable requirement for orientation of dipoles of water. The ideal case - maximal flow rate and is possible major length of a magnet gap.

3. Rate of flow.                     

The above velocity, is better, but at maintenance that of a dwell-time of system in a field. In magnets of the final sizes at high speeds the run time will be too little for formation aquacellas.

4. Frequency of change of a field.

Ideal case, when the field does not vary at all, but at present constructions of magnets it while is impossible, possible frequency therefore is indispensable minimally.

5. Field strength.

From a magnetic intensity the polyextreme dependence is watched. It is called by that at formation of aquacellas ions hinder, since of Lorentz force theirs moves not there, where it is necessary. Therefore ions are better for importing after formation of aquacellas, but here small relaxation time non-stabilized aquacellas hinders. Nevertheless, Sokolov watched, that the effect is almost identical if to import salts iron to processed water up to or after processing, and Shahov etc. have found, that the introduction in water of a coagulant is more useful after processing. Apparently, in both cases in systems already there was some of stabilizing ions. Besides under activity of Lorentz forces there is an accumulation opposite charged ions so, that there is an electric field orienting ions in the side, opposite to a magnetic field. And, at last, already formed aquacellas can be turn in a magnetic field bodily and to fail as on dipoles the orienting moment in one side and on stabilizing ions in another operates. From here polyextremeness of effect from field strength is not surprising.

6. Relaxation time.

The different relaxation time is stipulated by different stabilizing activity of ions depending on their concentration and nature. In solvate layers of colloid particles in absence of coagulation this time is not restricted, i.e. the layer thermodynamically is inconvertible. It is known, that many nonsoluble in water of matter, specially, of high molecular weight (for example, polyethylene) "are dissolves" globularly, forms not a molecular solution, and highly dispersive colloid dredge. The similar matters should steady magnetized water. Besides it is improbable, that aquacellas represent flat or filiform aggregates because of a high surface energy. Their existence in the view, contracted in a sphere is more probably. Then they will represent a precise duplicate of a colloid particle without a solid core at centre.

7. Poor reproducibility of experiments.       

Apparently it is called by that initial for processing the object contains miscellaneous quantity of aquacellas germs. In completely pure from aquacellas to system in a run time they can not be formed at all by analogy, for example, with the super cooled fluid in which one will not be formed of chips in absence of germs or of phase interface. This moment plays, probably, very major role, allowing from above-stated, that the present expedients of processing are very far from an ideal.

There is one more essential factor sharply lowering reproducibility of experiments with "memory" of water. The process of mutual amplification of orientation of molecules in aquacella and adsorption of ions on its surface accrues, as snow-ball, therefore the slightest change of exterior requirements is strong on it influences. Besides at a Brownian motion of aquacellas their almost each coming together gives in a tightening in space between them is of the same name of charged ions (because of influence of counterions). At removal of aquacellas from each other between them it appears again born aquacella that of a sign of a charge, i.e. aquacellas are capable to be propagating itself in favorable requirements. This effect for biology has the very relevant value, since alive organisms, in basic, consist of water and have permanently effective generators of aquacellas as particles of a blood and other colloid particles.

The dilution of a solution containing aquacellas can under the relevant requirements not only not reduce their quantity in a solution, but the concentration them can even grow, if the dilution happens enough slowly, that the water could properly "to remember" the structure. In this connection there are understandable some completely surprising experiments, bound with "memory" of water. Some biologically active substances, being diluted in water solutions maintain the activity. All would be anything, but cunning the experimenters so have diluted a solution, that in a vessel did not remain of any molecule of matter... and the activity has remained! The water "has memorized", that of it was diluted.

Experiment of the author.

Thus, as a first approximation, the magnetized water can be imagined as suspension mechanically of strong plates of aqueous associates (aquacellas) with that feature, that these associates, sticking together among themselves is opposite by charged surfaces, in the beginning are consolidates, then "are diluted". The presence of aquacellas, apparently to detect by filtering of magnetized water is easiest. The effect magnetization should be exhibited in diminution of filtration rate at pores clogging of the filter by aqueous associates.

In the described below experiments the filters "a cyan strip", beforehand wetted in distilled water within one half-hour were utilized. The town water was withstood with day at room temperature and magnetized (1 m/s, 1000 oersteds). In particular time took from a portion (100 mls) and filtrated. Filtration rate scored in 2 minutes after a beginning of a filtration. On a figure 5.3. the results of three parallel experiments in a time dependence the after magnetization are shown. By triangles mark results of a filtration of a town water missed through a magnet gap in absence of a current in an electromagnet (the check). Each point on the diagram corresponds to filtering of a new portion of water through the fresh filter.

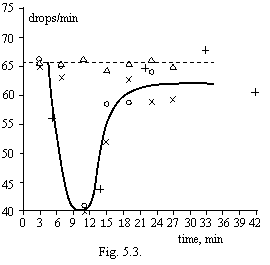From a figure it is visible, that immediately after processing will be formed aquacellas with the size less than 1-3 microns freely transiting through the filter, which one are aggregated and in 10 minutes after processing reach the sizes sufficient to block pores of the filter, that gives in sharp diminution of filtration rate. In further aggregates become or too major (do not dive into pores of the filter) or, on the contrary, very small owing to fracture. The filtration rate again will increase. By results of this experiment it is possible to estimate counting concentration of aquacellas, forming the after magnetization of water, by accepting their size equal 1х1х0.1 microns. It has appeared not less than billion aquacellas in 1 cm³.

Such experiment was realized also: immediately after processing the town water is filtered, thus the filtration rate has decreased all on 6% (in limits of an error of experiment), then the filtrate after 5-7 minutes again was filtered. The filtration rate has decreased already on 34 %, apparently, at the expense of enlargement aquacellas, past through the filter at the first filtration.

Resume

The magnetic field not "works", and only instigates formation of aqueous associates, i.e. plays a role of a trigger. At formation of aquacellas the energy is not spend, and is exude. The constitution can to itself be presented them as a solvate layer of colloid particles unfolded in a plane or contracted in a sphere. After formation aquacellas coagulates, are enlarges, the stabilizing charge on their surface is neutralized the oriented structure of aqueous associates becomes labile and gradually aquacellas fail.

Because of low-level concentration aquacellas such properties of magnetized water, as viscosity, density, latent heat of vaporization etc. practically do not vary. At the same time, contained in it aquacellas will render clout on processes, bound with formation of new phases, adsorption, coagulation, and also in biological systems.

The author hopes, that the enunciated hypothesis will help the interested researchers to govern concentration of aquacellas in water from maximal up to zero, i.e. to learn secrets of "alive" and "dead" water.

6. STEPPED PROCESSES in a WORLD ON an EXAMPLE of a COAGULATION of COLLOID SYSTEMS.

Aliasing of processes in a world we apparent always and everywhere. Watching any phenomenon it is possible guaranteed to state: «all will pass, will pass also it».

Idiosyncrasy of aliasing, ensuring advance, is that circumstance that each subsequent stage is essentially or in principle differs from the previous stage.

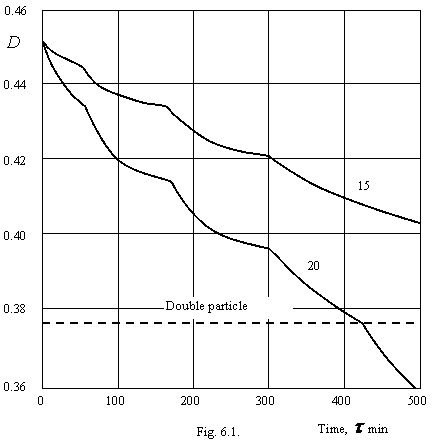At a coagulation of colloid systems the aliasing of this process is exhibited clearly at efficiency of collisions of particles less unity (slow coagulation). Our experiments on a slow coagulation of anatase (modification of titanium dioxide) in 25 mmole/l a solution KCl have shown fracture of a kinetic curve in a point D=0.3747 (D₀=0.4535). This fracture corresponds to formation of double particles on all volume of suspension. Really, on the equation (2.1.1.) this part of the book, optical density at a double particle D₂=0.3779, that with precision 0.85 % coincides experiment. The analysis of major number of literary data confirms aliasing of process of coagulation. My experiments uniquely display, that the process of a sluggish coagulation goes in such a manner that in the beginning in all system the double particles, then quater etc will be formed. It indicates an applicability of a rule of phases of the Gibbs to process of coagulation of particles, and double, quater etc. the particles should be viewed as separate «phases» of system.

On a figure 6.1. the kinetic curves of a coagulation of suspension of titanium dioxide are shown at concentration of potassium chloride less threshold. Numerals for curves - concentration KCl in mmole/l.

As it is visible from a figure 6.1. on these curves fractures up to a double particle clearly are watched. It managed to be detected because of absence of intermixing of a solution and fast response of a method of measuring. The explanation of these fractures by a state transition of a double electrical layer of colloid particles because of major time of coagulation is impossible, at which one the fractures are watched. It is necessary to refer fractures of kinetic curves, apparently, to a step change of coagulative ability of particles, bound with a state transition of their solvate layer having, apparently, composite structure and consisting from several underlayers (in our example 3), become revealed in accordance with destruction of a solvate layer by counterions, penetrants into it. The considerable strength of a solvate layer of anatase particles is confirmed by a major time term, after which one the fractures are watched. For the benefit of this assertion speaks that fact, that the fractures are watched at particular time of coagulation. The ions of potassium dive inside of a solvate layer and disturb its structure. The velocity of a diffusion of ions in a case concerning to a figure 6.1. practically does not depend on concentration them in volume of a colloidal solution and together with a high monodispersity of colloid particles gives in fractures of a kinetic curve to a particular instant.

At concentration of an electrolyte below threshold, the process of a coagulation is determined by quantity of a repulsion, bound with a charge of particles. The equilibrium aggregates can not reach the major sizes, since between particles of aggregate the considerable electrostatic repulsive force operate. In accordance with diminution of a charge of particles with magnification of concentration of an electrolyte, the equilibrium size of aggregates grows. Up to a threshold of a coagulation the dense aggregates of a noncrystalline type are gained, since such aggregation of small number of particles energy is favourable. At presence of a residual electrostatic barrier, the particles do not remain in place of their first touch, and take most energy favourable standing.

In work (А.А. Shternberg. The collection of papers: Growth of crystals. v.5, M., 1965, page 179) is shown, that the most stable formation of a noncrystalline type is the regular icosahedron containing 13 particles. The packing density of particles in such aggregate very high also has not analogs in crystalline structures with a close packing of particles.

When the concentration of an electrolyte exceeds threshold, the energy barrier becomes so small, that the particles in aggregate remain in a standing of their first touch. It gives in formation quasicrystal filiform, flat and volumetric aggregates with small density. The not spherical shape of aggregates is easily detected, if in a basin to leave a small bubble of air not hitting on a reading beam of light and intermixing solution at gyration of a basin. Thus the aggregates are oriented across a light ray and the optical density varies at rotational displacement of a basin on 180⁰ so strongly, that the recorder writes a curve of breadth almost on half of scale.

As a result of experiments the following picture of a sluggish coagulation was clarified. At first till all to system the aggregates from a double particle will be formed. Only after terminating this process the coagulation of double particles among themselves with formation of aggregates from 4 particles starts. Further process goes similarly and the aggregates from 8 particles will be formed. After that the surprising appearance is watched. The aggregates from 8 particles stick together with formation of aggregate from 16 particles, inside this aggregate the regular icosahedron from 13 particles will be promptly formed, the coulomb repulsion for «superfluous» three particles becomes such, that they abandon aggregate. The process very much resembles decay of a nucleus many protons.

To test, whether has a detected appearance universal character or concerns only to a special case, the experiments were well-handled with a hydrolysis of industrial solutions titanylsulphate with the content TiO₂ 200 g/l. That prehydrolysis the solution represents a dark-brown fluid with a strong light absorption in the first series of experiments an industrial solution it was necessary to dilute with distilled water till 6-36 g/l TiO₂. At concentration of titanium dioxide is higher 30 g/l kinetic curves have the S-figurative shape with an induction period, which one take place in actual production process of production of pigmental titanium dioxide.

By results of experiments the following mechanism of a hydrolysis is clarified. Crystallites of a metatitanic acid the size 40-50 Å in the beginning will be formed (on our data of radiography analysis they in further practically are not incremented in the sizes). Then these crystallites coagulates pairwise on all system, further pairs are agglomerated in tetrahedrons, which one in further will forms aggregates from 8 particles. Then at coagulation they are re-forms, by forming a regular icosahedron from 13 particles, throwing out superfluous 3 particles. The size of a regular icosahedron makes in a diameter 100 Å, i.e. is peer to a radius of action of Van der Waals forces for crystallites of a metatitanic acid, which one we have determined from experiments of peptization of this acid by a triethanolamin. Further regular icosahedrons are joined in pairs, and then the pairs will forms a tetrahedron from 4 icosahedrons. These aggregates containing 52 initial crystallites appear very stable against further aggregation and in technological solutions коагулируют only during water delivery at the end of a hydrolysis.

For verification that the coagulation of crystallites of a metatitanic acid is the basic feature of a hydrolysis, an industrial solution diluted not with distilled water and 0.8 % by a solution of agar up to concentration 36 g/l TiO₂. During observation within 18 clocks of change of an optical density of a solution it is not discovered. This experiment has shown, that in requirements, when the mobility of ions has not varied, and the colloid particles have lost mobility (solution has consistence of dense kissel), the process of a hydrolysis (aggregation of particles) ceases.

№	Label of points of a kinetic curve	exp.	theor. on (2.2.5.)	Comment
1	Beginning of a horizontal segment	0.0118	0.0116	Tetrahedron from 4 icosahedrons
2	Before a horizontal segment	0.0083	0.0082	Double icosahedron
3	In inflection of curve	0.0066	0.0065	Icosahedron from 13 crystallites
4	Breakpoints from an induction period up to inflection of curve	0.0039	0.0040	The 8-th particle
5		0.0019	0.0020	Tetrahedron from crystallites
6		0.0009	0.0010	Aggregate from two crystallites
7		0.0005	0.0005	Single crystallites

The initial segment of kinetic curves of a hydrolysis goes with acceleration. It Table 6.1.

is stipulated by that the forces of Van der Waals are additive and in accordance with magnification of number of particles in aggregate the attraction between aggregates will increase. At reaching the size of aggregates to an equal radius of action of these forces (icosahedron 100 Å) the further magnification of the size does not give in magnification of attractive forces. Therefore, the formation of icosahedrons should be watched near to an inflection point of a kinetic curve of a hydrolysis, that is confirmed experimentally (table 6.1.).

Optical density of a solution (36 g/l TiO₂) in points of fracture of a kinetic curve of a hydrolysis.

On electron-microscopical snapshots samples of a metatitanic acid from a horizontal segment of kinetic curves the tetrahedrons from 4 icosahedrons are well visible. The quantity of crystallites in a icosahedron is difficult for counting up because of limiting magnification.

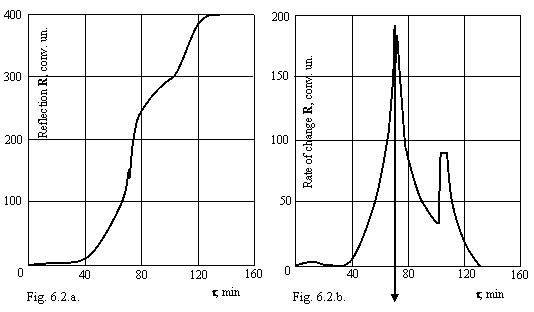
For verification of made deductions on actual technological solutions the experiments with a thermal hydrolysis of a solution containing 206 g/l TiO₂ were posed. On installation fixed process of a hydrolysis, measuring not light transmission, and reflection it from a solution which is taking place in a glass cylindrical vessel. The requirements of a hydrolysis strictly corresponded to the regulation indication on carrying out of this operation in production of pigmental titanium dioxide. Record of a kinetic curve executed simultaneously by two recorders EZ-2, one of which noted an integral curve, another - differential. 6 hydrolysises in total were realized to be convinced, that the obtained effect is not contingency. As the reproducibility of experiments was high, on a figure 6.2. the kinetic curve in integrated (a) and differential (b) to the shape, identical to all executed experiments is given.

Converts on itself attention sharp diminution of a reflection power of a solution about an inflection of a kinetic curve of a hydrolysis, and this spring is performed in time less than second, about what speaks so high negative value of a derivative, that it did not managed to lock in even at presence on a recorder 11 spare scales (blanket height of a line with arrow on a figure 6.2.b. more than 4 meters). After spring the process goes from smaller value of intensity of scattered light and with smaller velocity.

The author incurs boldness to state, that the icosahedrons will arise in any processes, the weep which one is impeded by any factors.

Thus, the process of a hydrolysis represents strictly ranked aggregation of particles in space both in time and in this sense confirms global world regularity of the time-space order of any processes and phenomenons.

The colloid systems from alive organisms are separated by one step, for which one are necessary hundred millions years. But if this step is made, the further strife for resources accelerates of evolution in thousands time.

7. INFLUENCE of MAGNETIC And PULSING ELECTROSTATIC FIELDS

The author in 1974 has made discovery under the name "Influence of a magnetic field of the Earth and electrostatic fields on coagulation kinetics" and has submitted the appropriate application for recognition of discovery. But system of a science throughout corrupts. Try to present to a solid magazine perfect scientific article. If in the authors there will be no known name any mafia man from a science, your article will be never published, what value it would not represent. Official oppressor of new ideas will send you the review (unsigned to not risk by esprit de corps), in which will be refused in the publication. For me, for example, cowardly grave digger of discoveries directly has declared what to make an application it is necessary, when will become the academician. Only the democratic Internet has allowed to be published by everyone, whom not laziness, and me including. The truth thus arise the large dump of scientific rubbish, but, having rummaged in it, always it is possible to find mass of original ideas and stimulus for the further work.

Influence of a magnetic field of the Earth. The experiments carried out on modeling system in environment 0.1 М KCl on green suspension of anatase, which stability raises after dilution within day at the expense of gegenions desorption from of a solvation layer. In 10 minutes the after of a beginning coagulation cuvette suspended on a long string (17 fluctuations one minute) and resulted in oscillatory movement along magnetic force lines of the Earth or across them. After fluctuations within 10 minutes measured optical density of suspension, which corresponds to an experimental point on a figure 7.1. The beginning of an axis of ordinates is chosen arbitrary. 1- fluctuations along a field, 2 - fluctuation across a field. 

At fluctuations across a magnetic field of the Earth the acceleration of process coagulation is clearly shown. Irrespective of stability initial suspension, the effect of increase of speed coagulation at fluctuations of cuvette across a magnetic field of the Earth remains, approximately, constant and equal 26%. The disorder of experimental points is connected to insufficient accuracy of installation cuvette with a solution in cuvetteholder. The effect of acceleration at application of constant magnets in the same conditions is so significant, that the difference in optical density is easily found out by a simple eye. 

It is interesting to note, that the probably direct decision of a question: whether is the reason of acceleration coagulation the polarization of a double electrical layer or of a dipole solvation layer. The relaxation time of a double electrical layer changes from 10^-5 up to 10^-7 sec (N.A. Izmailov. Electrochemistry of solutions. М., 1966, page 122). The relaxation time of a outside solvation layer makes, on my data, quantity, about 1 second. It is determined by supervision in optical microscope. The particles of anatase suspension in microscope look by diffraction ringlets with intensive Brownian movement. In a field of vision microscope the set of collisions of particles without any seen interaction between them is observed, but in rare cases it was possible to see effective interaction. It looks as follows. Cooperating particles, the relative speed of which rapprochement at the given moment is insignificant, suddenly begin synchronous Brownian movement, forming as though dumb-bell with distance between particles about several diameters them diffraction of rings. Then in time, about 1 second, the particles are pulled together and form the steady aggregate. 

Hence, if to change direction moving of cuvette or direction of a vector of a magnetic induction with frequency, intermediate between 10^-5 сек and 1 second, the effect of acceleration coagulation at the expense of polarization of a double electrical layer should be remain, and at the expense of polarization of a dipole solvation layer this effect will disappear. The check has shown that for the given system even at application of constant magnets with frequency of change of a vector of a magnetic induction making only 6 sec^-1 effect is absent. From here is follows, that the magnetic field accelerates coagulation at the expense of polarization of a solvation layer of colloidal particles.

Influence of a pulsing electrostatic field. The results of experiments on influence of a pulsing electrostatic field on coagulation of suspension titanium dioxide in 0.1 М a solution KCl are given on a figure 7.2.

On a figure 7.2.: 1 - coagulation in absence of a field, 2 - coagulation in pulsing a field.

After coagulation within 10 minutes cuvette placed in a Petri dish and closed by a plexiglass plate. During next 10 minutes coagulation went under action of a pulsing electrostatic field created by friction about plexiglass of the paper filter. It is clear from figure 7.2. effect of increase of speed coagulation in an electrostatic field has appeared twice more and makes 52%, therefore it is well fixed even visually. Such increase of speed has appeared sufficient for nonequilibrium course coagulation and, after removal of a field, the weak effect peptization within two minutes is found out, i.e. is observed convertible coagulation. Peptization can be explained to that at removal of a field the structure of a surface of a hydrate layer of anatase particles is partially restored. The application of pulsing electrostatic and magnetic fields in technological processes connected to a condition of an outside solvation layer of colloidal particles can be very effective. For example, in the given system such speed coagulation is reached which can not be achieved at any concentration KCl.

The described effect in 52% is caused by an electrostatic field of small quantity, though the outside field was strong enough. It follows that the external field is compensated by a field arising inside conducting environment, what is anatase suspension with electrolyte. Therefore at a constant external electrostatic field, inside cuvette the field is absent. Shielding of this field occurs in time relaxation of conducting environment, which is equal /K, where K - conductivity of environment, - it permittivity. From here is follows that the field inside of cuvette lags behind an outside electrostatic field. The effective field working on particles will be proportional to size of backlog. Thus, the pulsing electrostatic field, the same as also magnetic, causes acceleration coagulation at the expense of polarization of a solvation layer of colloidal particles.

The described discovery has huge importance, is especial for biology. Anyone alive organism represents complex colloidal system. Each cell of organism has a membrane bearing double electrical and a solvate layer. All properties of a membrane, at the end, are defined by properties of a solvate layer and ions. The discovery makes scientific base under the uncountable observant facts, which orthodoxies are inclined to attribute false-scientific to imaginations or mysticism. For example, professor Chishevsky, which on an example of the large number of the facts has proved influence of solar activity on many biological processes on the Earth, and has died, spit upon by the orthodoxies, which accused him of all mortal sins. At the same time, now authorities are compelled to warn the population about forthcoming magnetic storms. At any movement across magnetic force lines of the Earth we magnetized our internal environment. A mobile water stream, rivers and ocean currents is effective enough magnetized and always contains aquacellas. Especially this phenomenon has an effect in high latitudes of the Earth, where the magnetic force lines are condensed and are directed almost perpendicularly the surface of ground. The especially strong influence of magnetic processing should have an effect for origin and development of embryos, where the slightest changes of conditions have far-reaching consequences.

8. Apparatus for separation of liquid isotopes

Surprisingly, that the good ideas frequently come in a head in many years after realization of the applicable experiments when to play back or to update them already it is impossible. Why these ideas do not come at once? The answer I see in the depravity of the  system of science. Frequently coming with work complain to mother:

- Mama, do not give to work.

- And you do not раy attention and work.

Then it was necessary long to explain, that it is necessary to write the sham records, to go in business trips to implant the own inventions, to drink with a management of plants, that they have signed the act on which one we «trained staff» and made other useful for a plant of business make something out of thin air, sittings of senatus academicus, recalls on works of competitive organization, the conferences both sittings and other devildom did not leave at all time for creative scientific activity. When I have become, at last, by the free artist and anybody by nothing is obliged, then began substantial creativity. After that lyrical digressions it will become understandable, why the idea in 40 years after my occupations by colloid chemistry was born.

The principle of operation of the apparatus though is original, but very much is simple in fulfilment and is shown on a figure 8.1 on an example of a single cell of separation customary and heavy water. The unit cell of separation consists of a vessel 1, filled water. On water the platform 2 floats. On a platform tube 3, approximately, 1 cm diameter and same altitude is fixed. The platform has of such weight, that the top of a meniscus of water in a tube almost coincides the upper shear of a tube. The activity of the device is illustrated by a figure 8.2.

At vaporization of water from upper face of a film of surface tension on a underside of this film the heavy water is concentrated, since its vaporization from a concave meniscus is hindered because of padding connections with adjacent molecules. The heavy water flows off downwards on an internal surface of a film of surface tension and is stored in lower point of a meniscus so long as under operating of gravity will not be torn off as a drip. This drip, certainly, deliquesces at motion on bottom of a vessel, but in absence of a considerable convection this phenomenon does not hinder separation. The visually described effect is inconspicuous, but the device neatly fixates an alternation of an optical density of a liquid at dip of «drip».

The apparatus as a whole is the rectangular container, filled water, in which one the platform with numerous tubes. Thus, is simultaneous on bottom of a vessel thousand «drips» of a heavy water can simultaneously drop. During activity the platform is automatically travels to bottom of the container and slightly floats up, since density of a liquid is step-by-step augmented. At achievement by a platform of bottom of the container the process of separation customary and heavy water is as a matter of fact repeated a uncountable number of times, that guarantees a high degree of separation. The apparatus works independently and does not require service and power supply. For preventing a considerable convection of a liquid the thermal insulation of the apparatus is advisable. Naturally, that in conditions of the customary research institute I could not analyse presence of a heavy water because of uncountable obexes of our security system.

9. Theory of originating protolife on the Earth

This theory concerns to systems, which one yet not living, but already and not dead. The eternal problem of originating of life on the Earth till now is not resolved because of the insecure methodical approach to the solution of this problem. The scientists attempt to make a supermixture from separate amino acids and hope, that in this mixture life spontaneously will be engendered. For certain it is possible to assert, that it will not happen. The solution of a problem of an origin of life lies through a solution of a problem of a genesis protolife, being a link between the living and not living nature.

For originating protolife we will need water with dissolved in it by a small amount of any salt creating meager concentration of cations and anions, colloidal particles (for example, of volcanic ashes) and outside a power source (photons, radioactive decay of isotopes or ultrarays). The principle of originating protolife is identical to any «nutrition», which one should be gas. At the presence of Hydrogenium will arise «hydrogenous protolife», in azote - «nitrogen», in sulphur dioxide - «sulfuric», in ammonia - «ammoniacal» etc. We here will be interested by originating «carbon» protolife on the basis of usage qua of «feed» of carbon dioxide.

At hit of colloidal particles in water on their surface are adsorbed potentialdeterminant ions, which one give to particle an electrical charge (more often negative, approximately, 300 mV). The polar molecules of water are marshaled along lines of force of an electrical field and will formes thermodynamically a steady solvate layer by thickness, approximately, 300 . The electric field strength in this layer 10⁷ V/m (chapter 5 in section «Colloidal systems»), i.e. near to a surface of a particle it has properties of a solid, which one in process of deleting from a surface step-by-step loses. Because of intensive Brownian motion of a micelle, the counterions in solution can not reimburse electric charge of a colloid particle at an adsorption on a surface of a solvate layer, therefore particle has a residual electrokinetic potential about 30 mV.

At approach two negatively of charged micelles in space between them the cations are tightened, which one also will formes a particle, similar micelle, which one more correct to call aquacelle, since it has not a solid core (figure 1a). Thus, any approach of micelles and aquacelles generates formation of aquacelles, i.e. last are intensively propagates itself. And at approach two aquacelles of one sign of a charge arises new aquacelle of the opposite sign of a charge. Though the weight concentration of aquacelles does not exceed 0.01 %, the countable concentration makes, approximately, 1 billion of aquacelles in 1 cm³ of solution.

At a following stage aquacelles with opposite charges will formatives dipoles and thus considerably augment a life time of aquacelles (figure 1b). The dot lines shown a direction of axes of water dipoles in a solvate layer.

Dipoles of aquacelles, inclusive different cations and the anions, being attached to each other by unlike poles will formatives a chunk of a three-dimensional network, it would be possible to call which one «protocellule» (figure 2). On a figure of a line mean chains of dipoles aquacelles. Thus protocellule has the even greater strength, than separate chain of dipoles. It quite can accept the spherical form from power reasons and in this case will become very similar to a living cell.

Here it is necessary to recollect catalysts of chemical reactions. The catalyst will be most effective only in the event that its geometrical form of a molecule most approaches for the given chemical process. Any distorting of this form decontaminates («poisons») catalyst. For example, in a cell indicated by number 1 of a figure 2 the most eligible conditions for synthesizing from carbon dioxidal and water, for example, molecule of a glucose C₆H₁₂O₆ can be added up. Then the given cell will and henceforth emboss molecules of a glucose, which one, apparently, will encourage formation of cells similar on mother in other places of protocellule or others protocellules. Therefore cell - catalyst can be esteemed, as the great-grandmother DNA, and made by means of its molecule, as the great-grandfather of enzymes.

Apparently, that under the described scheme of activity protolife production of any organic compounds, for example, methane and hydrocarbons with allocation in atmosphere superfluous in these processes of oxygen is possible. It is possible, that by reserves of gas and oil the mankind is obliged to just protolife.

Any organic matter at incineration in environment of oxygen basically will formatives water and carbon dioxide. Therefore with the help of catalysts and external power sources which are capable to burst any chemical bond possible implementation of reverse process: synthesizing of organic compounds. Thus, protolife though is not usefulness life, but at a molecular level has all attributes of life: reduction of an entropy at the expense of external energy, reproduction, competition for power and alimentary resources, strife for existence and evolutionary selection. Here it is necessary to mark, as the present life at a molecular level does not differ from the lifeless nature. That will be further, it is better to ask of the Darwin.