18. FORMATION of SOLID BODIES

 

If the formation of molecules in modern chemistry one way or another explained, the reasons of formation of solid bodies, on a view of the author, are unconvincing, as at a level of molecules all connections are already saturated and, behind elimination of "hydrogen bond" and the electrostatic bond is not present sufficient energy opportunities to form of molecules solid macrobody.

 

 


From a point of view of the above-stated types of a chemical bond, in actual objects, the connection, basically, never can be completely saturated because of the steric factors. Therefore always there is an opportunity not only to collect from molecules macrobody, but also for it macrobody the ability to affixing of foreign atoms is maintained, that is exhibited in its ability to a sorption, dissolution, chemical activity etc.

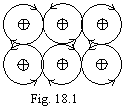
Let's analyses some examples. On a figure 18.1 the variety of a one-electron bond in metals is figured.

The trajectory of a casual electron is shown arrows. From a figure it is visible, why the metals enable major plastic strains. The similar connection is carried out in metal simultaneously many electrons in the most miscellaneous directions.

In overwhelming majority of non-metallic matters the connection of component particles has certain directedness, therefore they friable. It is possible to formulate a blanket apparent rule: are more saturated the connection in a molecule - the more feeble connection between molecules. For example, structure NH3 (fig.18.2.a). In it only one connection is not saturated and in standard conditions NH3 - gas.

 

 

 

 

 

 

 

 

 

 

 

 


In H2O (fig. 18.2.b) two connections are not saturated and in standard conditions H2O - fluid. In NaCl  (fig. 18.2.c) not saturated already three connections, therefore NaCl - solid matter. For BeO (fig. 18.2.d) besides that three connections are not saturated also the beryllium donates one electron to oxygen completely, i.e. in solid oxide BeO except for saturation of one-electron bonds the strong electrostatic bond acts also. Therefore BeO will forms a very strong crystal lattice in matching with NaCl.

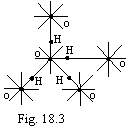
As an example, on a figure 18.3 the crystal lattice of ice as a tetrahedron is figured. Each atom of oxygen is enclosed by four atoms of hydrogen two of which one are arranged close. All one-electron bonds for oxygen and hydrogen in this case are saturated.

 

 


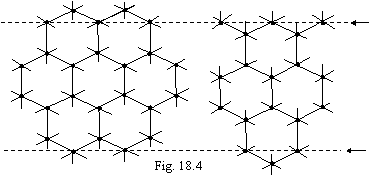
Following of added up tradition, we shall consider in conclusion of this section of structure of diamond and graphite. As the atom of carbon has in a torus four electrons that, joining each atom with four neighbors in tetrahedral structure with completely saturated connections (it will be a two-electronic bond), we shall receive structure of diamond, where each atom of carbon has 8 electrons. If is carried out not two-electronic, and one-electron bond between atoms of carbon, the flat hexagonal lattice will be formed, in which one half of atoms of carbon has 5 electrons, and other half - 6, as shown in a figure 18.4.

The structure of graphite is gained by superimposition of planes against each other (along dashed lines). Thus the atoms of carbon having till 6 electrons, will not form connection, and the atoms having till 5 electrons appear against each other and will forms an one-electron bond. Thus, in a lattice of graphite all atoms of carbon have till 6 electrons, accordingly, the strength it is much lower, than for diamond.

Here are circumscribed, behind a deficiency of a place, only principled fundamentals of new views on a chemical bond and are given examples of a small number of compounds. The reader can check the author on a word, that he has analyzed major number of different chemical compounds and has not found anything that contradicts above-stated, though the chemistry has business with huge variety of compounds.

 

18.1. About "surface gas" of liquids and solids

 

Concept about surface gas of liquids and solids.

It helps to explain their many properties and to give the quantitative theory of these properties. Atoms or molecules, of which the solids or liquid consists, are capable to jump out of volume on a surface and freely enough to move on it, jumping from one potential hole in another, as a power barrier to such jumps small. If energy of activation of transition in surface gas large enough, the concentration of molecules in surface gas, accordingly, is small, and it is possible to consider it as ideal bivariate gas. 

Concentration of particles in surface gas.

Speed of transition of particles in surface gas:

                                  (18.1.1.),

where: C0 - surface concentration of particles of substance, 1/cm2

           C - concentration of particles in surface gas.

Speed of condensation from surface gas in volume of substance:

                                     (18.1.2.).

The balance is established quickly, since the process of condensation has no energy of activation:

                                       (18.1.3.).

 (18.1.1.) and (18.1.2.) we shall substitute in (18.1.3.) and we shall find:

                                    (18.1.4.).

On the Arrhenius:

, , since E2=0                     (18.1.5.),

where: E1 and E2 - energy of activation, accordingly, transition of a particle in surface gas and condensation in volume of substance, erg/mol.

(18.1.5.) we shall substitute in (18.1.4.) and at  (particle same), we shall find:

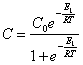                                    (18.1.6.).

At E1>>RT (18.1.6.) will accept a kind:

                                    (18.1.7.).

Than closer to a condition fusing of a solid or boiling of a liquid, the below E1 and at E1=0 (18.1.6) will accept a kind: C=C0/2 that is obvious.

The energy of activation of carry of a particle in surface gas will be equal to the sum:

                                    (18.1.8.),

where: Q - energy necessary for break of connections with atoms of volume of substance at given temperature, cal/mol,

            F - specific free surface energy.

QT we shall find from the following reasons. To break off connections in a liquid at given temperature, it needs to be heated up to temperature of boiling and to evaporate, then to cool of vapour up to initial temperature, but without condensation. To break off connections in a solid, it is necessary it to heat up to Tmel and melted. In the formed liquid of connections are so weakened, that they can be neglected as a first approximation and molecule or atoms to consider practically free. The formed liquid should be cooled up to initial temperature without crystallization in a solid. Thus it is necessary to notice, that the free specific surface energy is automatically taken into account also. Therefore as a first approximation (without cooling gas or liquid from temperature of phase transition up to initial temperature). For concentration of particles in surface gas such simplification is allowable:

 cal/mol                        (18.1.9.),

where: cp - thermal capacity, cal/g×deg,

           M - molecular weight, g,

          T=Tph-T, where Tph - temperature of phase transformation, deg,

          0 - specific heat melting or evaporation, cal/mol.

Formally, we can attribute energy on (18.1.9.) to one atom. Thus we shall take into account, that at an output in surface gas the atom has one degree of freedom, third of this energy therefore suffices, it and will be energy of activation:

                      (18.1.10.).

 Having substituted (18.1.10.) in (18.1.7.), we shall find:

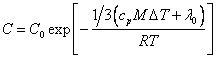                  (18.1.11.).

Expression (18.1.11.) fairly far from temperature of boiling or melting, near to them it is necessary (18.1.10.) to substitute in (18.1.6.):

                  (18.1.12.).

It is easy to show, that:

                           (18.1.13.),

where: C0 - surface concentration of particles of substance, cm-2,

           d - density of substance, g/cm3,

          N0 – Avogadro constant, mol-1,

          M - molecular weight, g.

Surface tension.

Energy on the equation (18.1.10.), come on one particle:

                  (18.1.14.).

Having multiplied number of particles on (18.1.13.) on energy come on one particle on (18.1.14.), we shall receive:

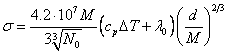erg/cm2       (18.1.15.).

Expression (18.1.15.) is possible to treat, how surface tension without account of surface gas, which does not bring in contribution in .

In the table 18.1.1. the calculated and experimental values of a surface tension for water and mercury are submitted at 200С in erg/cm2.

Table 18.1.1.

Substance

Is calculated on (18.1.15.)

 

Tabulated value

 

Water

70

72.75

Mercury

444

472

 

For flying liquids to neglect concentration of atoms in surface gas it is impossible, since at change of a surface these atoms do not render influence, therefore results of account on (18.1.15.) it appear overestimated. For example, for ethyl alcohol the calculated value on (18.1.15.) 56.7 erg/cm2, and experimental 22.8 erg/cm2. It is obvious, that the effective concentration of particles on a surface influencing a surface tension, will be:

                              (18.1.16.),

where C is determined by expression (18.1.12). If it to substitute in (18.1.16.) and to multiply by energy comes on one particle, we shall receive:

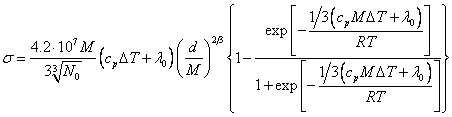  (18.1.17.).

The known empirical expression, suitable for many liquids, looks so:

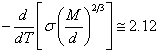                         (18.1.18.).

If to differentiate on temperature (18.1.15.), as more simple, in comparison with adjusted (18.1.17.), we shall receive the same result:

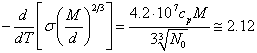            (18.1.19.).

Evaporation heat.

Energy necessary for heating and evaporation for a liquid at temperature of boiling we shall find on a known ratio:

                          (18.1.20.),

where:  - average thermal capacity of a liquid, cal/mol×deg,

          Tliq = Tboil – T,

          tv – evaporation heat at temperature of boiling, cal/mol.

Similarly for a solid:

              (18.1.21.),

где:  - average thermal capacity of a solid, cal/mol×deg,

       T1 = Tmelt – T,

       melt – melting heat, cal/mol,

       T2 = Tboil – Tmelt.

The formed gas as a result of processes (18.1.20.) and (18.1.21.) has superfluous energy:

                                 (18.1.22.),

where:  - average thermal capacity of gas, cal/mol,

           T = Tboil – T.

If we shall take into account this circumstance, in result we shall receive for liquids:

                        (18.1.23.)

and for solids:

            (18.1.24.).

As thermal capacity of bodies depends on temperature, we have received approximate value evaporation heat. To have exact value, it is necessary to know experimental value of the expended integrated heat.

Comparison calculated on (18.1.23.) and (18.1.24.) and experimental values of evaporation heat of different substances at different temperatures is submitted in the table 18.1.2.

Table 18.1.2.

Substance

Temperature, 0С

 tabular

computed

CdCl2

568

41.2

41.1

Cs

28.7

18.82

19.9

FeCl3

304

16.5

16.6

H2O

0

10.77

10.80

H2O

25

10.51

10.53

H2Se

-65.7

5.34

5.61

Hg

-38.9

15.20

15.73

Hg

25

14.54

15.43

KBr

735

48.9

51.1

 

Saturated vapor pressure.

It is obvious; that values determined on the equations (18.1.23.) and (18.1.24.) will be energies of activation of transition of particles from surface gas in a gas phase, accordingly for a liquid and solid. Therefore we shall arrange one more check of validity of the equation (18.1.23.) for further use. We use tabular data for water (evaporation heat at 1000С 9717 cal/mol, =9.971 cal/mol×deg, 1 cal = 4.1858 joules). Results of comparison of account on (18.1.23.) with the tabular data at different temperatures are submitted in the table 18.1.3.

Table 18.1.3.

Temperature, 0С

Experimental evaporation heat, joule/g

The calculated evaporation heat, joule/g

0

2501

2492

5

2489

2480

10

2477

2469

15

2465

2457

20

2454

2446

25

2442

2434

30

2430

2423

40

2406

2399

50

2382

2376

100

2257

2260

 

The data of table 18.1.3. show that the equation (18.1.23.) is acceptable to rough accounts.

Let's consider that the surface gas is ideal bivariate gas and submits to the known equation of a gas condition:

                                    (18.1.25.),

Number moles in surface gas:

                                  (18.1.26).

In (18.1.25.) let's substitute (18.1.26.) and value gas constant R:

                                 (18.1.27.),

where the pressure is expressed in atmospheres. If in (18.1.27.) let's substitute (18.1.12.) and (18.1.13) with the account (18.1.23)., we shall receive finally:

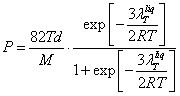                        (18.1.28.).

For solids it is necessary to take into account not (18.1.23.), and (18.1.24.).