The constitution of
atom is a corollary of aspiration of any system to a minimum of a potential
energy, instead of any selection rules or certain composition of quantum
numbers. The aspiration to a minimum of a potential energy is sufficient,
exhausting for exposition of atoms.
"In a basis of
an operation by notion about the character of a state of an electron in atom
with the help of four quantum numbers (n, l, ml,
ms) lies the principle of the prohibition (or principle of
elimination), formulated by Pauli. According to a Pauli's exclusion principle,
in atom there can not be two electrons, the state which one would be featured
by completely identical combination of values of termed above four quantum
numbers; even one of them should accept different values". "About a
systematic of particles", М., 1969, page 12. It seemed, the official physics can shout:
"Hurrah!" and to figure electronic configurations of all atoms. But
is not present! Nothing is gained, will not apply yet rule of Gund:
"...the electrons in limits of a given subshell aim to lie so that value
of their summary spin was maximal..." (Ibidem, page 14). Feel an
inconsistency with a Pauli's exclusion principle? One requires a miscellaneous
state of electrons, another - identical. "On the basis of a Pauli's
exclusion principle in combination to a rule of Gund it is possible to give the
scheme (so-called, ideal scheme), describing allocation of electrons according
to values of quantum numbers" (Ibidem, page 14). Well, now that, is
possible to shout "hurrah"? Certainly, is not present! The following
quotation is rather characteristic for orthodox thinking. "Nevertheless,
the tendency was widely spread to consider the ideal scheme just normal, while
the actual periodic system was considered as abnormal, as a special case of an
abnormal, irregular development of periodicity. This inconsistency, certainly,
braked further development of the theory of periodic system. To overcome this
inconsistency, it was necessary to refuse not only notion about a dominant role
of a main quantum number n (here to you, grandmother, and main quantum
number! - V.K.) in definition of sequence of shaping of electronic
configurations of multielectronic atoms, but also that generally energy state
of an electron in multielectronic atom is always predominantly determined by a
main quantum number" (Ibidem, page 21). For the first time a dominant role
of a main quantum number has refused V.M. Klechkovsky, by formulating (n+l)
- rule: "This regularity most clearly is uncovered, if a grouping of
quantum levels of electrons in atom to subordinate to a principle grounded at
integrating in one group of levels with identical value of the sum main (n)
and orbital (l) quantum numbers" (Ibidem, page 22). All this waste
of time with a bedding of rules against each other has, at the end, pessimistic
finale: "We should, first of all to mark, that the actual scheme of
shaping of electronic configurations of atoms in some cases appears not so
strictly series, as it should stream from (n+l) - rule. Three
basic types of discrepancies are watched" - further they are numbered
(Ibidem, page 40).
|
|
|
|
|
|
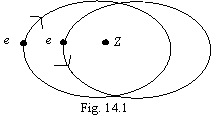
Let's consider two-electronic atom figured on a figure 14.1. It is
possible to show, that the orbits of electrons are not elliptic, but only
ellipsoidal, however, for simplicity of calculations it is possible to accept
by their elliptic, exchanging an actual orbit by an equivalent ellipse. Thus
we, naturally, any more can not expect for rigorous quantitative concurrence to
experimental data, but those basically is impossible at interaction of many
bodies. On a figure mechanical and of the magnet moments of electrons are figured
antiparallel, since only at such standing the system will have a minimum
potential energy. Interaction of magnet moments to allow here we shall not be.
As a first approximation, without them the results will be received quite good
as against a quantum mechanics, which one is salvaged only by viewing of this
interaction. "The identity of identical particles gives in a quantum
mechanics in particular interaction between them, termed by an exchange
interaction. ... The exchange energy has not classic analog.... It is
impossible to interpret quantities termed sometimes as exchange density, as
customary densities of charge: they can be and complex.... The exchange energy
is electrostatic - it is proportional to a quadrate of elementary charge....
The more degree of overlapping of wave functions ("of electronic
clouds"), the more exchange energy.... Due to an exchange energy in the
same system can exists both attractive force and repulsive force".
"Physics of a microcosm", "Soviet encyclopedia", М., 1980, page
42-43. In spite of the fact that in this problem of physicists fully darken, as
a matter of fact there are only two versions of interpretation of an exchange
interaction: or this attractive interaction of antiparallel of magnet moments
of electrons (or the repulsion parallel), or is necessary to introduce a new
view of interaction. For many reasons both these of version do not approach at
all for a quantum mechanics, therefore the exchange interaction has not
physical sense.
Position of electrons relevant fig. 14.1, one in pericentre of an orbit,
another - in an apocenter. The blanket binding energy of both electrons Etie1,2 is
similar to expression (13.1), will make expression:
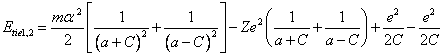(14.1).
In (14.1) last two
terms mutual cancel out, since the electrostatic energy interaction of
electrons among themselves urges an electron in pericentre "to be
attracted" to a nucleus, and electron in an apocenter - "to be
repelled". Exchanging in (14.1) C through eccentricity 
, after transformations we shall
discover:
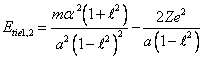(14.2).
Differentiating
(14.2) on 
and equating a derivative to zero point, we shall discover a
semimajor axis of a stationary orbit:
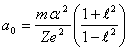(14.3).
By substituting
(14.3) in (14.2), we shall discover a binding energy in a ground state:
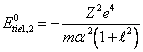(14.4).
Apparently, that 
is the sum of the first 
and second 
potentials of ionization
helium-like of atom. we already know for hydrogen-like atoms, therefore:
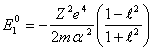(14.5).
From (14.5) or (14.4)
on experimental potentials of ionization it is easy to find eccentricities of
stationary orbits (numeral at e means nuclear charge helium-like of
atom): e2 = 0.6143, e3 = 0.4859, e4
= 0.4141, e5 = 0.3667, e6 =
0.3325, e7 = 0.3062, e8 = 0.2853, e9
= 0.2678, e10 = 0.2534, e11 =
0.2408.
In calculation on one
electron, is similar (13.4), we shall note:
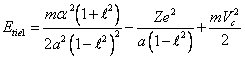(14.6),
and designate:
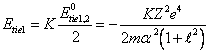(14.7),
from (14.6) with the
registration (14.7) we shall discover Vc, differentiated it
on ,
we shall be convinced, that the maximum value 
corresponds 
and we shall discover:
(14.8).
Allowing, 
and 
at radiation of photons, comparing with
(14.8), we shall discover:
(14.9).
By substituting
(14.9) in (14.7), we shall receive:
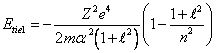(14.10),
then energy of a
photon:
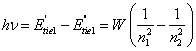(14.11).
The formula (14.11)
is valid for any electron in any atom, if W to consider as function n1
and n2. This equation can be received and from more blanket
reasons. The radiation of a photon for atoms containing more of one electron
though will be determined by transition of a given electron to more
low-altitude orbit, but the value of energy of a photon will depend any more
only on an difference of a binding energy of a given electron, but also all
remaining electrons, as there is a self-acting restructuring of all atom.
Besides an electrostatic energy interaction of electrons among themselves
simultaneously varies also. Therefore for any electron in any atom:
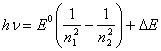(14.12),
where 
E - some function from n1
and n2, and E0 - electron-binding energy in
a ground state. Equating (14.12) anyone known semiempirical or absolutely
empirical-formula dependences, is successful approaching for exposition of
spectrums, we always shall discover E in an explicit
view. The known dependences usually enable as a matter of fact not integer
values n1 and n2. For example, the frequencies
of lines in spectrums of alkaline elements are determined by the formula:
,
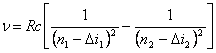where i - correction (so-called quantum
defect). For each element of values of the correctionы are various,
besides they are various and for the same element depending on value of an
orbital quantum number l. R - constant of a Rydberg. G.E.
Pustovalov "Atomic and nuclear physics", Publishing House of the
We shall not be so
was easily, as it is done by a modern physics, to change to idea quantumness at
first discrepancies with the test data, though the official physics has occasions
to maintain more loyalty, since it considers quantumness as the initial reason
of behavior of an electron in atom. The alternate physics considers occurrence
quantumness as the inevitable resolution of conflict between aspiration of an
electron to a minimum of a potential energy and impossibility of radiation of a
nonintegral photon. Not tampering with nonintegral n1 and n2
we shall consider W as function n1 and n2,
then from (14.12) we shall receive (14.11). W at n2
and n1=1 numerically
is peer to electron-binding energy a nonexcited state (E0),
more correctly, to potential of ionization at removal of a given electron and
depends on a degree of excitation of an electron (position of its orbit).
The equation (14.11),
in opinion of the author, is more preferential than any other semiempirical
expressions on following circumstances:
1. It has extreme
clear physical sense.
2. Integer-valued n1
and n2 allows easily interpreting spectral lines.
3. As the change of a
binding energy of a given electron imports the solving contribution to energy
of a radiated photon, the value W always is close value E0.
In connection with
enunciated, there is a sense to compound the table of values 
, which one is very comfortable for
the analysis of spectrums.
Table 14.1.
|
n2 n1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
1 |
0 |
0,750 |
0,889 |
0,938 |
0,960 |
0,972 |
0,980 |
0,984 |
0,988 |
0,990 |
1,000 |
|
2 |
|
0 |
0,139 |
0,188 |
0,210 |
0,222 |
0,230 |
0,234 |
0.238 |
0,240 |
0,250 |
|
3 |
|
|
0 |
0,049 |
0,071 |
0,083 |
0,091 |
0,095 |
0,099 |
0,101 |
0,111 |
|
4 |
|
|
|
0 |
0,022 |
0,034 |
0,042 |
0,046 |
0,050 |
0,052 |
0,062 |
|
5 |
|
|
|
|
0 |
0,012 |
0,020 |
0,024 |
0,028 |
0,030 |
0,040 |
|
6 |
|
|
|
|
|
0 |
0,008 |
0,012 |
0,016 |
0,018 |
0,028 |
|
7 |
|
|
|
|
|
|
0 |
0,004 |
0,008 |
0,010 |
0,020 |
|
8 |
|
|
|
|
|
|
|
0 |
0,004 |
0,006 |
0,016 |
|
9 |
|
|
|
|
|
|
|
|
0 |
0,002 |
0,012 |
|
10 |
|
|
|
|
|
|
|
|
|
0 |
0,010 |
The analysis of
spectrums is convenient for conducting under the following scheme: а). We detect electron-binding energy
on stationary orbits of given atom. b). Any spectral line of this atom is
translated in energy of a photon expressed in electron-volts on the formula: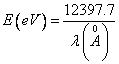 
and
from the formula (14.11) W is discovered, using the table of values . The
value D should be picked from the table so
that W was closest value of any electron-binding energy on a stationary
orbit. Thus, for each spectral line we shall discover W and values n1
and n2.
Usables this scheme
for the analysis of spectral lines of helium. Under the formula (14.4) on one
electron in a stationary state the binding energy 39.5 eV is necessary. To
receive spectral lines at E0=39.5 eV, the completely
identical and simultaneous excitation of both electrons of helium is necessary,
that is very improbable. Other energy state of atom of helium at which one the
binding energy of the first electron makes 24.6 eV (first potential of
ionization), and second 54.4 eV (second potential of ionization) energy-wise is
equivalent binding energies of both electrons on 39.5 eV, since in the sum the
energy is identical: 79 eV. We would have completely diverse world, if the
magnetic interaction of orbital electronic currents would not steady electrons
on an orbit 39.5 eV. Then the electrons have preferred to take miscellaneous
orbits: 24.6 eV and 54.4 eV. Therefore excitation of any electron instigates
similar reorganization of orbits and in a spectrum of helium we should to
observe the relevant series of lines. Besides in anyone it is enough strongly
excited atom (at small n1), we should watch lines relevant W
13.6
eV, since from a point of view of an electron on a high-altitude orbit, the
atom is represented hydrogen-like. As at removal of an electron from a nucleus
there is a reorganization of remaining electronic orbits in structure relevant
to atom, engaging the previous standing in the table of elements of the
Mendeleyev (at ionization of Zinc the structure will be formed cuprum-like, at
ionization of cuprum – nickel-like etc.), in spectrums of elements with
sequentially incremented nuclear charge the picture of lines of the previous
element with the relevant bias in short-wave area and expansion of a gap
between lines is iterated. In table 14.2 the data of decryption of some lines
in a spectrum of helium are given.
Table 14.2.
|
n1 |
n2 |
Wave length of a photon, (A0) |
W,(eV) |
|
1 |
3 |
584.33 |
23.87 |
|
3 |
5 |
7065.20 |
24.68 |
|
3 |
6 |
5875.63 |
25.32 |
|
3 |
7 |
5769.60 |
23.69 |
|
3 |
10 |
5015.678 |
24.47 |
|
3 |
4 |
4685.75 |
54.00 |
|
4 |
7 |
5460.73 |
53.94 |
|
4 |
8 |
4916.00 |
53.81 |
|
4 |
8 |
4960.32 |
54.33 |
|
2 |
3 |
6678.149 |
13.36 |
|
2 |
4 |
4916.00 |
13.45 |
|
2 |
4 |
4960.32 |
13.29 |
|
2 |
6 |
4120.82 |
13.54 |
|
2 |
7 |
4026.192 |
13.41 |
|
2 |
8 |
3888.645 |
13.60 |
As well as it was
necessary to expect, the values W are close to values 54.4 eV, 24.6 eV
and 13.6 eV.
|
|
|
|
|
|
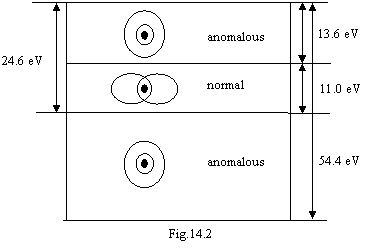
Table 14.2 displays, that the atom of helium has three systems of spectral
lines. The figure 14.1 explains system of spectral lines of normal atom of
helium with Е0=24.6 eV. The systems of spectral
lines with Е0=54.4
eV and 13.6 eV concern to abnormal atom of helium. It will be formed as
follows. The energy 11 eV (see formula 16.5 in chapter 16) is indispensable for
busted of a magnetic attraction of electrons. At deriving this energy the
electrons any more can not take a standing relevant to a figure 14.1 and will
forms a following configuration: the outside electron takes a quasistationary
orbit with a binding energy 24.6–11=13.6 eV, therefore its energy levels
practically correspond to levels of atom of hydrogen. The inner-shell electron
takes an orbit with a binding energy 54.4 eV, therefore its energy levels
correspond to a hydrogen-like atom with nuclear charge +2. Thus, the abnormal
helium though and metastable, but is stable enough. It is necessary to allow
for it, those spectral lines of neutral helium to not confuse with lines of
neutral hydrogen or should be single-pass of ionization helium. The enunciated
situation is figured schematically on a figure 14.2 where the areas of
existence of normal and abnormal helium are figured. The outside electron is
gone on radius of the first orbit of the Bohr, and interior on an orbit with
radius twice smaller.
14.1. Effective charge and influence of
magnetic orbital interaction
As the
electron-binding energy in atom is proportional to a quadrate of effective
nuclear charge, it is possible to note the ratio:
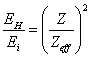(14.1.1),
whence:
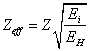(14.1.2),
where Ei
- binding energy (ionization) of an electron in i-th atom or ion with a
charge Z from a certain energy level, EH - binding
energy (ionization) of a hydrogen-like atom with a charge Z from an
energy level that the number.
For lithium in a
ground state: Ei=5.39 eV, EH=13.6 eV, Zeff
= 0.629. The diminution of a charge is stipulated by proximity of
inner-shell electrons to outside. As the attractive force to a nucleus is
proportional to a charge in the first degree, and the repulsive force from
inner-shell electrons is inversely proportional to a quadrate of distance, they
strongly reduce an ionization energy.
For Li+
in a ground state: Ei=75.7 eV, EH=54.1 eV, Zeff
= 1.182. In this case magnetic orbital attraction of two electrons,
which have stayed in lithium, gives in increase of ionization energy (effective
charge). Thus, the presence of inner-shell electrons gives in diminution of an
effective charge and the orbital magnetic interaction of a given electron with
other electrons of atom yields the same activity as increase of an effective
charge.
Energy of connection
of an electron at any level of a hydrogen-like atom ЕН we already know (formula 13.17).
Apparently, that the similar formula for any electron in any atom will differ
only by value of an effective charge Zeff instead of Z.
A difference of these binding energies:
E=EH –Ei
(14.1.3),
From (14.1.3) we
shall discover Еi:
(14.1.4),
where Е0 - ionization energy of atom of hydrogen.
From (14.1.4) it is
visible, that the effective nuclear charge varies not only depending on a
degree of ionization, but also from an energy level, on which one there is an
electron, i.e. from distance up to inner-shell electrons and shape of an orbit.
Energy of a photon,
which one is radiated at transition to lower layers, is peer to difference of a
binding energy on final and original level. For this case the formula (14.1.4)
starts a view:
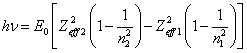(14.1.5).
Near to a ground
state the levels of energy are arranged densely, therefore effective charge
remains practically identical. For this case (14.1.5) is simplified:
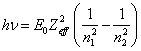(14.1.6).
Naturally, that the
formula (14.1.5) will give precise values of energy of radiated photons, but
practically to use to it is to deceive myself, since Zeff
depends from n and while can be retrieved only from experimental data.
It is more useful to use the formula (14.1.2), that on an effective charge to
judge a constitution of atom. Then it is possible to construct the theory for
analytical definition of an effective charge and the formula (14.1.5) will
become very useful.
Here it is necessary to mark one more key difference in views on
radiation of photons by atom in the modern and introduced reader to alternate
physics. The modern physics considers, that the reason of radiation is the
transition of an electron to other orbit (more correctly, in other state, since
it does not recognize neither orbits, nor electron, as integrated particle in
atom), and the radiation of a photon is a corollary of such transition.
Apparently, that, in this case, the reason of transition of an electron in a
new state remains vague, besides photon appears in an inconvenient standing, as
should "to remember" a original state of an electron, which one can
be by anyone. The quantum mechanics as the solutions of a Schrodinger equation
gains not metastable, and invariable "excited" states of electrons in
atom, therefore is forced to explain instability of such states by interaction
of an electron with virtual particles born in vacuum.
The new physics considers, that the atom radiates a photon owing to
aspiration to a minimum of a potential energy, and it can radiate any photon in
limits solved centrifugal velocity of an electron and a requirement of
diminution of this velocity in an integer of time, and the new orbit with a
binding energy by more close to bottom of a potential well will be a corollary
of radiation. In all sincerity it is necessary to recognize, that to a modern
physics at all from an arm to be engaged in clearing up of causal connection of
radiation of a photon and state of an electron, as at anyone apportionment the
photon should "to foresee" a final state of an electron or "to
remember" initial. As it manages to do - official science to explain be
not capable and it is not agglomerated to do, since a quantum mechanics -
statistical theory disclaiming a determinism in a microcosm (see of an
indeterminacy relation of the Heisenberg).
Some words are necessary for telling about thin structure of spectral
lines, which one the author associates (in particular) to precessional
movements. The reason of a precession of an orbit of an electron is the
declination of a rotation axis of an electron to orbital plane that, in turn,
is a corollary of a motion of a mobile electron on a screw line. The trajectory
of an electron in a plane, perpendicular precession axis is similar to
Lissajous figures and depends on a relation of frequencies of a precession and
circulation of an electron around of a nucleus. Except for a precession of an
orbit of an electron, simultaneously there is also precession of a rotation
axis of the electron (orbits component its neutrino, see chapter about
"elementary" particles) and precession of rotation axes the neutrino
from which one consists an electron. The precessional movements split levels of
electron-binding energy with a nucleus on a series of sublevels, as the
mechanism of their formation has many similar features with the mechanism of
formation of invariable orbits of an electron in atom (allowed orbits). Are
available some more reasons resulting in to split of levels of energy, on which
one to stop we shall not be, for example, one of the reasons is the interior
constitution of an electron, which one very much resembles atom, in which one
function of electrons fulfill a neutrino. Here only we shall mark, that the
official physics of one of the reasons of thin structure of spectral lines
considers relativistic increase of electronic mass in velocity function. But
this increase happens not quantize, and smoothly, therefore, in any way can not
create additional quantized levels of energies exhibited as close set spectral
lines. "The thin structure of spectral lines is quantum relativistic
effect. It is explained by result of activity of two factors: by 1) interaction
of an own magnet moment of an electron with a magnet moment of orbital motion
of an electron; by 2) relativistic dependence of electronic mass on
velocity". N.I. Kariakin etc. "The brief manual on physics",
"Higher School", М.,
1962, page 350.