ATOMS, MOLECULE

13. The THEORY of a HYDROGEN-LIKE ATOM

From this chapter it will become clear, that the modern theory of a hydrogen-like atom grounded on a quantum mechanics and the set up theory of atom of alternate new physics on relation to each other stands heels over head. Who from them stands on a head - to judge to the reader. The quantum mechanics is as a matter of fact suitable only for the description of atoms and their nuclei, since the behavior macro objects cannot be described by this theory - they "classic", and to elementary particles it is impossible to apply owing to, that: "...the quantum mechanics is not applicable to the description of processes described by the sizes of areas of their passing of the order 10^-13 cm and less". (N.I. Kariakin etc. Brief reference book on physics. "Higher School", М., 1962, page 417).

Much from that is set up below, with success can be applied to the description of space systems.

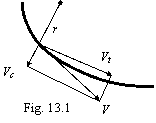
The equation (2.2) is deduced for circular orbits, when the velocity vector of an electron is perpendicular to radius - vector. For orbit of the arbitrary form (figure 13.1):

                                          (13.1),

where V - speed of a body on orbit.

The vector V on two related orthogonally components are decomposable: a tangential velocity V_t and centrifugal speed V_c so, that:

                                               (13.2).

In spite of the fact that the Bohr enabled a capability of motion of an electron with an aliquot moment of momentum and the modern physics approves it, we shall not sin against the fixed laws of the nature, especially fundamental. As the mobile electron has an angular momentum , it and remain to those on any orbit, including in a ground state (circular orbit). Earlier we were convinced that the principle of conservation of moment of momentum is fair even at motion of a body on a straight line. For an arbitrary trajectory of an electron (if an electron not relativistic), this law will look so:

                                                   (13.3).

By substituting (13.3) and (13.2) in (13.1), we shall discover:

                                       (13.4).

The known law that a system aims at a minimum of potential energy and on achievement it is taken a steady (basic) condition, requires essential elaboration included therein, that thus there should be a dissipation of energy at a rate of a difference of energy in initial and ground state, i.e. the system should be opened, instead of insulated. If a dissipation of energy does not take place, bottom of a potential well the system can not achieve (for example, the pendulum will be rocked eternally) - it the energy conservation law requires. In mechanical systems the dissipation of energy takes place at the expense of friction, in space - at the expense of tidal and other forces, and in a microcosmos - at the expense of radiation of photons (or pairs an electron - positron, if the energy has enough for their formation). As only last term (13.4) distinguishes this equation from (2.2),  is that reserve, from which one there is a dissipation of energy of an excited atom by radiation of photons.

From (13.4): 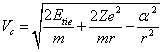                            (13.5).

Differentiated (13.5) on radius - vector and by equating a derivative to zero point, we shall discover, that maximum value V_c on a trajectory at , where r₀ - radius of a circular orbit in a ground state. By substituting this value in (13.5) and by agree that:

                                             (13.6),

where E⁰ - bond energy in a ground state, we shall discover:

                                        (13.7),

where V₀ - the speed of an electron on a circular orbit, i.e.  depends only on electron-binding energy.

Apparently, in this case, that energy of a photon:

                                                 (13.8).

Converting (13.8) with the registration (13.6) and (13.7), we shall discover:

                                                     (13.9).

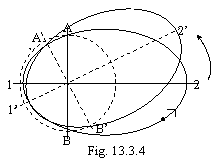
The same outcome we can receive and from (13.2), recording it for two orbits with V₁ and V₂ and allowing, that V_t to both these orbits is identical. It is easy to show, that if E_tie=0, the trajectory of an electron for a nucleus will be a parabola, if E_tie=E⁰ - circular orbit, and in all intermediate cases - elliptical orbits. For these orbits parameter of a parabola is peer to parameter of ellipses and is peer r₀, i.e. all orbits are intersected in two points to a diametrically opposite nucleus. In one of these points (where V_c is directed from a nucleus) there is a radiation of photons (in opposite - occluding) and transition of an electron from one orbit on another.

Let's suspect, that in a point of radiation of a parabolic trajectory is beamed only one photon which is picking up completely energy  (at it an electron at once will pass on a circular orbit). In this case energy of a photon will correspond to ionization energy of atom (limit of a spectral serial Lyman). From a principle of conservation of moment of momentum, moment of an electron, bound with V_c should be transmitted to a photon (simultaneously it and condition that the photon can be beamed only in the whole kind), therefore:

                                             (13.10),

where: N - the number of radiated photons,  in a point of radiation of a parabolic trajectory, since in it , r - has mathematical sense of radius for satisfaction of a law of conservation of angular momentum (it not radius of motion of an electron):

                                              (13.11).

We shall be now saved of it. From (13.10):

                                              (13.12),

By substituting in (13.12) r from (13.11), we shall discover:

                                                 (13.13).

Apparently, that number n of steady orbit, if not takes place of a further dissipation of energy:

n=N+1                                                   (13.14),

by substituting in (13.13), we shall receive:

                                                  (13.15).

Comparing (13.15) with (13.7), we shall discover K:

                                                (13.16).

By substituting value K from (13.16) in (13.6), we shall discover bond energy in hydrogen-like atoms depending on n, it is impossible to consider which one for our case as that by a quantum number, that in orthodox physics:

                                         (13.17).

Remaining - matter of technique. For example, by substituting (13.16) in (13.9) with the registration (13.6), we shall discover:

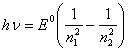                                           (13.18).

Thus, the radiation of photons takes place at motion of an electron in a potential well, and quantize is determined only by integrity of a photon and to a stationary constitution of atoms of any relation has not. The repetition factor of an angular momentum of an electron in the theory of the Bohr and quantum mechanics has not relation to an electron, and is only consequent that for all photons the angular momentum same and is peer , and the photon can be released or to be occluded only in the whole kind.

In this connection of logic of official science is faulty in the respect that it, watching excited atoms, mechanically transfers outcomes on a constitution of stationary atoms. We would make the same error, making conclusions about character of the man, when is observed him in an extremely exited state. If to be precise, the quantum mechanics is compelled so to do, since the solutions of a Schrodinger equation do not enable any "orbits" of an electron, except for a definite set. New physics considers, that in a ground state in atom the position of orbits of electrons is determined by a minimum of potential energy of a system as a whole, and quantumness is exhibited only in exited states of electrons. Let's put here quotation from: "Physics of a microcosmos", "Soviet encyclopedia", М., 1980, page 183: "It is necessary to mark, that, strictly speaking, in a quantum mechanics all allowed condition of atom (received at the solution of the applicable Schrodinger equation) - both basic, and exited, are steady, stable. The instability of excited levels is conditioned by interplay of atomic electrons with a virtual electromagnetic field, or with photon vacuum (?!). Therefore for the consistent description of quantum transitions in atom accompanied by radiation, it is necessary to allow for this interplay".

As we see, orthodox physics completely freely can explain something more or less understandable absolutely not clear, identifying boundary of nonsense with an inaccessible horizon.

Using (13.16), (13.6) and (13.4), we can calculate all parameters of possible orbits of an electron around of a nucleus, which one are shown in table 13.1. It is made simply: being set value n, from (13.16) we discover K, we substitute in (13.6), we shall discover electron-binding energy with a nucleus on this orbit, which one we substitute in (13.4) and, deciding a quadratic equation relatively r, we shall discover a perihelion and aphelion of orbit.

  Table 13.1

n	Orbit	Energy of connection ( in E^0)	Distance from a nucleus in perihelion  (in r0)	Distance from a nucleus in aphelion (in r0)	Eccentricity, е
1	Lyman	0	1/2		1
2	Balmer	3/4	2/3	2	1/2
3	Paschen	8/9	3/4	3/2	1/3
4	Bracket	15/16	4/5	4/3	1/4
5	Phund	24/25	5/6	5/4	1/5
…	...	...	...	...	...
	Bohr (ground state)	1	1	1	0
Relation from n

The eccentricity of orbit can be found from a known polar equation of curves of the second order. "In polar coordinates the curves of the 2-nd order have an equation , where p - focal parameter, e - eccentricity of the given curve, the pole is in focal point, the polar axis is directed from focal point to the proximate top". I.N. Bronstein and K.A. Semendiaev "Reference book on mathematics for the engineers and learner technical colleges", М., 1962, page 213.

We suppose in this equation focal parameter P=r₀, then:

             (13.19),        а                     (13.20),

where e - eccentricity.

Any other orbit parameters easily will be from known ratio for a parabola and ellipse.

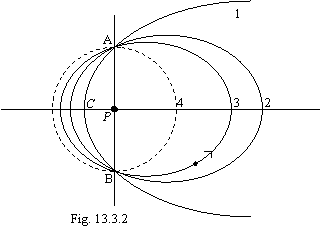
On a figure 13.2 5 orbits of an exited state of atom of hydrogen (their infinite set) and ground state (dotted line) are to scale figured. By arrow V_c labels a place of transition from one orbit on another at radiation of photons.

On a figure: 1 - orbit of the Lyman, 2 - orbit of the Balmer, 3 - orbit of the Paschen, 4 - orbit of the Bracket, 5 - orbit of the Phund, 6 - orbit of the Bohr.

The transition of an electron on any orbit - business of its own desire, but transition on near orbit in connection with an inertness of an electron is more preferential, that determines large intensity of lines  in each spectral serial, specially for high-eccentric orbits. The sizes of atom in any exited state a little differ from sizes of a nonexcited atom, then, as the official science assigns progressive increase of the sizes of an excited atom. The quantum mechanics results in the same expression for energy of a hydrogen-like atom, as simple theory of the Bohr:  (a) (N.I. Kariakin etc. "Brief reference book on physics", "Higher School", М., 1962, page 408). Accordingly, radius of a hydrogen-like atom will be proportional to a square of a main quantum number n.

Both at interplay of gravitational charges and at interplay of electrostatic charges (if mass of a central charge is much greater orbital) the following ratio (virial theorem) is executed: Е_rep = Е_bond = 1/2Е_att (b), where Е_rep - energy of repulsing, Е_bond - bond energy, Е_att - energy of attraction. If to accept for value of an angular momentum of an electron = mVr (c), substituting this value in (a), we shall discover for a ground state of hydrogen-like atoms under any theory (allowing, that  (d)):  (e). By substituting (b) in (e), we shall discover: , that corresponds to true. Thus, (c) really is an angular momentum of an electron in atom, and (d) - universal energy of repulsing.

In any spectral series it is possible to count up to hundred lines (their actual quantity indefinitely), thus the size of an excited atom should be increased not less, than in 10000 times, that leaves for frameworks of sensible physical sense (as a matter of fact, the modern physics considers, that the size of an excited atom radiating photons of a limit of any spectral series, including infrared, is perpetual, but does not advertise it). Look chapter 13.5 «Rydberg atoms».

If we have managed not only to arrange orbits of electrons in atoms in parallel planes (that it is possible to make with the help of a magnetic field), but also would make so that the big semi major axes of orbits too are parallel, the radiation of all atoms will be in space strictly distributed depending on energy of photons for given sort of atoms.

Now we shall demonstrate a regularity of a figure 13.2 and by that an inaccuracy of the official theory of atom. For this purpose at first it is necessary to determine tangents of slope angles tangents to orbits in transition points from one orbit on another. It is two intersection points of focal parameter P with ellipses. From known relations for an ellipse and allowing, that by the equation of focal parameter will be:

x₀ = C                                              (13.21),

where C - distance from centre of an ellipse before focus. Substituting (13.21) in the canonical equation of an ellipse and further in the equation by tangent to an ellipse in a point (x₀, y₀) after some transformations we shall discover:

tg =C/a = e                                       (13.22),

where a - semimajor axis of an ellipse, e - eccentricity of an ellipse. Thus, the tangents of a slope angle of orbits in intersection points with focal parameter numerically are peer to a eccentricity of an ellipse, for example (see table 13.1) the orbit Lyman has a slope angle to a horizontal 45⁰, and orbit of the Bohr, naturally, 0⁰. 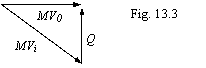Now it is easy to count up, as the energy of an electron will vary at radiation of a photon, using a law of conservation of impulse and calculating scheme introduced on a figure 13.3:

On a figure 13.3: mV₀ - impulse of an electron on an orbit of the Bohr, mV_i - impulse of an electron on any other quasistable orbit, Q - recoil impulse received by an electron at radiation of a photon by atom. Thus, at transition of an electron from any orbit in a ground state in this state the impulse of an electron will be:

mV₀ = mV_i∙cos                                          (13.23).

The change of energy of an electron will make:

                                         (13.24).

By substituting (13.23) in (13.24), we shall receive:

                                           (13.25).

In (13.25) V₀ it is possible to determine by two equivalent manners: or from equilibrium of an electron on a circular orbit:

                                              (13.26),

or allowing, that the spin of an electron is peer  (instead of half of this value!):

                                              (13.27),

where a₀ - radius of an orbit of the Bohr. To us is now more suitable (13.26) to substitute in (13.25) and to discover a difference of energies in eV. Simultaneously we shall substitute numerical values of constants and conversion factor an erg in eV (e_e = 4.80286×10^-10 CGSE, a₀ = 5.29172×10^-9 cm, 1 eV = 1.60206×10^-12 ergs):

E=13.605×e²                                            (13.28).

From 13.28 it is visible, that for an orbit of the Bohr (e=0) transitions to the same orbit do not change energy of an electron, and for an orbit Lyman (e=1) the photon with energy of an equal ionization energy is radiated. The same formula confirms the below-mentioned scheme of energy levels (fig. 13.4). For an orbit, for example, Balmer (e=0.5) at transition in a ground state the photon with energy 3.401 eV will be radiated, and that from this orbit to ionize atom it is necessary to expend energy 13.605-3.401 = 10.204 eV.

From a figure 13.3 it is easy to receive the formula 13.28 on change of a kinetic energy of an electron at transition to a stationary orbit if to take into account, that mV₀ = mV_i∙cos:

                             (13.28a).

The formula 13.28а displays, that the radiation of atom is a braking radiation. The electron loses a kinetic energy along an orbit, therefore photon is radiated perpendicularly to it.

The formula 13.28 allows considering with what level electrons transfer in a ground state at heat exchange at any temperature, utilizing the law Wien. We shall copy it for energy of a photon relevant to a maximum of radiation at a Kelvin temperature Т expressed in eV:

E_max= 0.42809∙10^-3∙T eV                                       (13.29).

By substituting 13.29 in 13.28 thus at 13.28 instead of eccentricity we shall substitute its expression through the number of an orbit from table 13.1:

                                                 (13.30).

From the formula 13.30 it is visible, that for n=1 (thus there occurs thermoionization of hydrogen) temperature 31780⁰ is necessary. At ambient temperature (293⁰К) the heat exchange in basic is yielded by photons radiated at transition in a ground state from the orbit № 10, and "relict" radiation (at Т=2.7⁰К) from an orbit № 108. These calculations display that at heat exchange the electrons are near to a ground state. In a considered occasion official physics anything intelligible to tell can not.

We have considered "fall" of an electron on a proton in a plane of normal section of a screw trajectory of a mobile electron. Precisely same result we shall receive and at "fall" of an electron on a proton lengthwise axis of screw trajectory of a mobile electron, i.e. in a perpendicular direction. Therefore, the same result will be and at "fall" under any arbitrary angle. Really, we shall start up an electron up to energy; equal potential of an atomic ionization of hydrogen, then under the formula (2.10) radius of a screw trajectory of such electron will be precisely to correspond to radius of a stationary orbit of an electron in atom of hydrogen. If such electron "will put on" on a proton, beforehand by losing an ionization energy, since the energy of its headway is peer to energy of a motion on coils of a screw trajectory, it will appear at the bottom potential wells, nothing differing from the electron which has hitting there from a perpendicular direction. Certainly, the differences of these two electrons can be noted on thin structure of spectral lines, since the slope angles of circumgyration axes of electrons and their precessional movement (both electrons and their orbits) will be various. These two trajectories of a motion of an electron to a nucleus differ as well by  that in first case of the photons are radiated in orbital plane, and in second - in a perpendicular direction, that is exhibited in effects (longitudinal and cross) Zeeman and Stark. Superimposing an exterior magnetic field on radiating substance (Zeeman Effect), we is orientated orbits perpendicularly to field. Therefore at one motion of an electron all orbit under activity of force of the Lorentz a little is squeezed, and at an opposite motion of an electron - is dilated. Then we shall watch a spectral line not , and in radiation along a field. At radiation across a field the same force of the Lorentz brakes transition of an electron to the necessary orbit with higher and accelerates an electron at transition with lower. Thus, the frequency shift of photons is compensated and across a field are watched three components and , and  (-component) twice more intensive  (-components). If a field feeble, neutralization can be incomplete and then we shall to watch some additional lines (abnormal Zeeman Effect).

The gravidynamic aspect above-stated is, that in length of any orbit of an electron one wave length de Broglie is stacked only, instead of the multiple, as is considered by a modern physics, if not to allow of multiquantum occluding at an intensive laser radiation (see for chapter rydberg atoms).

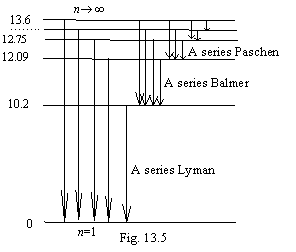
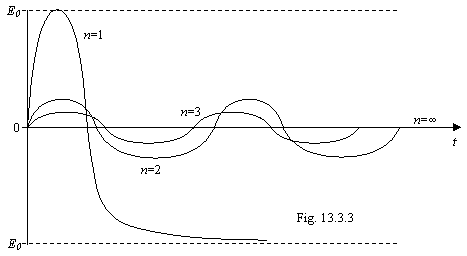
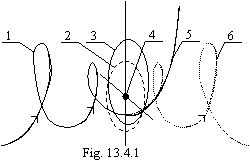
The energy levels of atom of hydrogen are shown on a figure 13.4. In matching with official representations, they are figured to within on the contrary, i.e. be posed from a head on legs and that is why. The law of the Kirchhoff stating, that the substance immerses those spectral lines, which one it radiates - fixed experimental fact. The atoms immerse the same lengths of waves, which one emits is a law of the Kirchhoff (1824-1887) and Bunzen (1811-1899). With this fact the level diagram фиг.13.4 is completely co-ordinates. For example, to receive an absorption line in a series of Phund, it is necessary to irradiate hydrogen with infrared rays with energy of photons less than 0.6 eV. Official the science assigns for deriving an absorption line in this series beforehand to excite atom by energy not less than 13.1 eV, and that and at all to ionize atom that enters a glaring contradiction with experiment. The exit of this inconsistency can be seen by own eyes in oof of paints of a surrounding world, be the official version of energy levels of electrons in atoms valid, and all paints here will vanish. About this inconsistency prefer to keep mum, since differently will be destroyed not only modern theory of atom, but also all quantum mechanics and will become vain those grandiose efforts, which one were spent for adjustment of the theory under experiment.

The energy levels of an excited atom should be densely arranged near to the basic nonexcited state; differently equilibrium thermal radiation is impossible. At standard conditions all atoms are in a ground state and that they could something radiate, the electrons need to be transferred even to the first excited level. If to accept on a faith the official scheme of excited levels, that the substance radiated, it needs to be heated on tens thousand degrees (10.2 eV for transfer of an electron of hydrogen in the first exited state corresponds to temperature approximately 100000⁰К). In the tendered scheme of energy levels it is enough for excitation of atom infinitesimal of action; therefore equilibrium thermal radiation of substance is possible down to temperature of absolute zero.

The official notions about energy levels considerably differ from introduced on a figure 13.4. The orthodox physics gives the following scheme of levels of energy in atom of hydrogen (see, for example, B.M. Javorsky and A.A. Detlaph "Manual on physics for the engineers and students of high schools", "Science", М., 1964, page 671).

The formula of the Planck for emitting ability of an ideal black body can trust not only owing to its correspondence to experiment, but also because from it as the corollary is gained the law Stephen - Boltzmann and Wien displacement law, which one also correspond to experiment. Therefore all spectrum of a thermal radiation is determined by transitions of electrons from one energy level on another. Thus has not value, whether such transitions in solid bodies, fluids either gases in molecules or separate atoms are carried out. For simplicity we shall consider a thermal radiation of atomic hydrogen. On notions of a modern physics to transfer atom of hydrogen in an exited state, the minimum portion of energy in 10.2 eV is indispensable. Thus the electron will transfer on the second level. At returning in a ground state the atom will radiate one most long-wave line of a series Lyman (1215.68×10^-8 cm). In a radiation spectrum we are more any other lines we shall not find out. To the indicated energy there corresponds temperature of an atomic hydrogen 78916 ⁰K. In the chapter dedicated to photons is shown, that the energy not less 5kT is necessary for formation of a photon. This fact enables simply to receive a Wien displacement law _max∙T=0.2896. For this purpose we shall note a requirement of formation of a photon: 5kT = h = hC/, whence _max∙T=0.2878. At house temperature (293 ⁰K) the minimum energy for formation of a photon is indispensable as a particle 5kT = 0.1267 eV. From these calculations it is visible, that the heat exchange by radiation and capture of photons at house temperature is impossible since the indispensable energy for this purpose in 80 times exceeds stock. Thus, the scheme of levels of atom of hydrogen of official physics is erroneous, since does not ensure heat exchange by radiation and does not correspond to a Planck formula. The scheme of levels introduced on a figure 13.4 indicates absolutely other behaviour of an electron in atom. For transfer of atom in an exited state the thermal energy even near to absolute zero of temperature suffices. To transfer an electron to the same second energy level the energy not 10.2 eV and 3.4 eV is necessary. Thus the electron will take an orbit Balmer, and in radiation we shall not see lines of a series Lyman, but completely all series, starting from a series Balmer and finishing a series of radiation in radiofrequency region. As near to an orbit of the Bohr the energy levels are arranged very densely, the discernibility of levels will depend on temperature of hydrogen and, with depression it, we can discover more and more close to a ground state of a line of radiation. The radio-frequency spectral lines in thousand times are feebler than spectral lines of optical range because of very small energy of quantum. Besides they can be watched only on a background of a more intensive continuous spectrum as hardly distinctive peaks. Under the literary data (for example, “Physics of space", Moscow, 1976, page 484) following radio-frequency spectral lines of hydrogen are experimentally retrieved (in brackets the transition between the numbers of energy levels relevant to this radiation is indicated) ~3.4 cm (9091), ~5,2 cm (104105), ~6 cm (109110), ~18 cm (156157, 157158). Results of calculation of a wave length of a radio-frequency radiation at the indicated transitions and according to the tendered scheme of energy levels: 9091 3.37 cm, 104105 5.20 cm, 109110 5.98 cm, 156157 17.49 cm, 157158 17.8 cm. Concurrence to an apparent wave length not incidentally since the numeration of levels of energy in official and new physics is identical, but the arrangement them is opposite. Here it is necessary to remind to the reader, that on notions of official physics radius of atom is proportional to a quadrate of a main quantum number (in this case - number of a level). Therefore for a level of 158 radius of atom of hydrogen will be increased in 25000 times and will make 1.32 microns, i.e. it can literally be felt. These data indicate that the modern theory of atom is erroneous. Е.М. Gershenzon in the article «Research of single atoms» (Soros Educational Journal, № 1, 1995) cites data, that the minimum energy quantum, observed in radioastronomical experiments, at transitions between high exited states of carbon atoms at  = 18 m corresponds 10^-19 ergs. Radius of such atom will make 28 microns at a main quantum number n = 733. Energy of electron connection will be 3.34×10^-17 ergs. It is easy to count up, that the indicated energy will be had with quanta of a maximum of a black-body radiation at temperature 0.242 К. Therefore any photon of relict radiation ionizes under consideration atom. Allowing huge concentration of relict photons the atoms with high exited states do not have any chances to keep integrity. Allowing, that the atoms beam photons with energy of relict radiation (2.7 К) from orbit № 108 (see. the formula (13.30)), the existence of neutral atoms with quantum numbers is higher 100 it is impossible because of their ionization by relict radiation. The reduced data demonstrate a regularity of a system of energy levels of atoms tendered new physics and inaccuracy of a quantum mechanics in the fundamental initial concepts. All inconsistencies with experiment fade if to allow for inspissating energy levels near to a ground state instead of far from it. Then, in this case, the speech is necessary for a message not about highexited atoms, and about very «cold» with temperature is not higher 0.2 К.

Introduced on a figure 13.4 scheme of energy levels explain also relative intensity of spectral lines, which one in due time have hurried to pronounce indefinable in model of the Bohr. Let's suspect that the electron is on an orbit Lyman and comes nearer to a point of radiation. In this point the electron should pass on more close to a ground state an orbit, but the transition probability is various, as is bound to necessity of deriving of an indispensable recoil impulse at radiation of a photon. Maximum likelihood to pass to an adjacent orbit, thus the most long-wave and intensive line from a series Lyman is radiated. Prolonging this process of series transition on adjacent orbits, we shall receive the most intensive lines of all possible series. Apparently, that the intensity of these lines gradually decreases, and the lines of a far infrared series practically do not differ on intensity because of a small difference in energy of levels. In radiated system of atoms always there will be such in which one an electron has transferred on any level, but in total of atoms a share of atoms in which one the electron has taken at once close to a ground state levels will decrease since probability of such transition small. Therefore in a given series intensity of spectral lines in the side more short waves decrease, and the lines near to a limit of a given spectral series practically do not differ on intensity.

To a critic of the official scheme of energy levels of atom of hydrogen it is possible to add following. Let's suspect that we supervise all completely series Balmer. Apparently, that on notions of official physics the electrons given this series everyone are on the second energy level and they nothing need to do as, to pass in a ground state with radiation a-lines of a series Lyman. Therefore intensity by this a-line should be not less summary intensity of all lines of a series Balmer that does not correspond to a real. Besides the returning force, proportional tangent of a slope angle of the graph of a potential energy, far from bottom of a potential well is significant, and it a ground state (at the bottom potential wells) is peer to zero point. Therefore any small external action outputs system from equilibrium because of an inspissation of energy levels for bottom of a potential well. The scheme of energy levels of orthodox physics explicitly contradicts the law of conservation of energy. Let's suspect, that we irradiate hydrogen with photons relevant to a limit of a spectral series Humphry (0.38 eV). These photons hydrogen is obliged to absorb under the laws of radiation. Thus the electrons of atoms will place close n=¥. How they itself behavior in further? Apparently, that they will give all possible spectral lines of all spectral series including a line relevant to a limit of a series Lyman (13.6 eV). Thus, our device, immersing small energy, will yield big of anything. It is a hard blow on orthodox notions. It is necessary to throw out in a waste basket all crazy theoretical gorges ХХ centuries, to return for hundred years back and to start all from a beginning. All modern physics represents a pyramid, standing sharp end on a basis of energy levels of atom of hydrogen. The author managed now to take out this basis.

To put the last point in an arrangement of energy levels of atoms, we shall find out physical sense of the known formulas of a thermal radiation of an ideal black body. The formula Raleigh - Jeans for a spectral density of an emittance of an ideal black body looks like this:

 ergs/cm².                                   (13.31).

Let's look, in what the physical content of this formula from a point of view of new physics consists. For this purpose we shall copy (13.31) through a wave length of radiation:

                                            (13.32).

The new physics states, that the wave length of a photon is peer to a circumference of a cross-section of its screw trajectory:

=2×r                                                (13.33),

where r - radius of a screw trajectory. Substituting (13.33) in (13.32), we shall discover:

                                            (13.34).

Thus, the formula Raleigh - Jeans describe a thermal energy of one degree of freedom (along a trajectory of a photon) coming on a cross-sectional area of a trajectory of a photon.

The formula of the Planck for a viewed case:

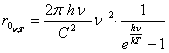                                      (13.35).

The formula (13.35) differs from (13.31) factor:

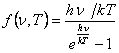                                           (13.36).

As a matter of fact factor (13.36) exchanges in (13.31) thermal energy on energy of a photon, and the denominator of this factor allows for a Boltzmann distribution law on energy levels near to a ground state of electrons. I shall remind, that the new physics considers, that here levels are strongly inspissated, therefore separate lines of radiation at transitions of electrons on these levels merges in a continuous spectrum. Only from here there are photons of a thermal radiation, and the orthodox physics can not answer a problem, such photons whence appears.

Now we shall understand with a "excited" electron and we shall look, whether it can radiate or to immerse photons, and also "to bear them with itself". The term "an excited electron" is extremely unsuccessful for the reason that the excited electron on the structure by nothing differs from not excited. On the other hand, it is completely inapplicable to such super excited electron, which one at all has come off atom, i.e. to a mobile electron. Relating an opportunity of radiation or absorbing of photons with change of a kinetic energy of an electron, rotary around of a nucleus, we doom ourselves to an infinite walk on a maze of logic docks, without any hope to find any exit. Therefore it is necessary at once to refuse viewing a kinetic energy of an electron, and to consider as its universal potential energy of repulsion. In this case we are forced to view all associates on interaction, i.e. system: an electron - nucleus (atom as a whole). The viewing of a potential energy only of electron without the associate on interaction is senseless. Analogy to an electrical oscillatory circuit radiating a radio wave here is pertinent. Without change of a potential energy of an electric field in the condenser and potential energy of a magnetic field in an inductance coil the radiation is impossible. At the same time, radiates radio waves a oscillatory circuit as a whole, instead of its any part. Thus, radiates or immerses photons atom as a whole, instead of its any part, and electron photons with itself has not.

The repetition factor of value  of a moment of momentum of an electron on a "allowed" orbit as a matter of fact means, that the electron in accordance with transition to more high-altitude orbits is covered by the increasing number of photons, more correctly by their moments of impulses. As the jumps at once through some levels are possible, it means, that some photons with small energy, combining, give a photon with big energy. In this case non-radiating transitions should not be watched. Apparently, that the similar notions are erroneous - moment of momentum of an electron on "allowed" orbits is identical except for circular orbits with an aliquot angular momentum for of rydberg atoms.

Comments of the author to chapter 13:

1. The orthodoxes themselves have put a bomb under a quantum physics.

In connection with elaboration lasers the existence so-called of rydberg atoms was revealed. They metastable also exist in a very rarefied space gas cloud. In natural earth conditions they will not be formed. The principle of their formation is simple and obeys to the theory of atoms of the Bohr. The atom occludes a photon with angular momentum h/2. The photon fades, and its energy is transmitted to an electron, which one will take higher energy level concerning a ground state. The angular momentum of a photon can not vanish together with it, and is transmitted to an electron. Thus, at series occluding of photons the orbital electron is allotted with a multiple of moments of a photon, that completely corresponds to the theory of the Bohr. The levels of energy are inspissated far from a nucleus. In this chapter the theory of atoms is given, where the levels of energy are inspissated near to a ground state and is shown, that these notions adequately mirror experimental observations. Both theory of the Bohr, and theory of atoms of a quantum physics are applicable only for of rydberg atoms. The orthodoxes so endeavours to adapt the theory under the final formulas of the theory of the Bohr (thus incriminating last in an inaccuracy), that have not noticed, how have put a bomb under a quantum physics. Soon they realize the error, but the clock-work already ticks and hardly will manage something to be collected from wreckages of a modern wave quantum mechanics. Apparently, that the favourite method of the low schoolboys of adjustment under the answer this time with adult uncles has played a malicious joke.

2. Angular momentum of an electron on elliptical orbit.

The calculations of angular momentum of an electron on elliptical orbits of hydrogen-like atoms can bodily be borrowed from chapter 21.0.1 for similar calculations of angular momentum on elliptical orbits of space bodies, since the physical principles are identical to these objects. Energy of attraction of an electron to a nucleus instead of (21.0.1.3) will be E_att = Ze²/r, then instead of (21.0.1.6) it is possible to record: L = (Ze²m_e× b²/a)^(1/2), where L - angular momentum of an electron on elliptical orbit, m_e - electronic mass, a - semimajor axis of orbit, b - semiminor axis of orbit. But b²/a = p - focal parameter, identical for for all orbits (figure 13.2). From here we make a conclusion, that the angular momentum of an electron on any orbits remains to a constant and is not spent for radiated photons, which one gain a angular momentum at the expense of radial component of speed of an electron V_c .

13.0.1. Theory of heat radiation and degradation of oscillators

Orthodoxes at any opportunity kicks classic physics, which one, ostensibly, is unfit to explain many phenomena, in particular, heat radiation of an ideal black body. Here I want to kick a Planck formula for emittance of a black body. This formula - favourite child of orthodoxes, as for the first time in it was utilised representation about quanta.

The formula of the Planck for radiant exitance of an ideal black body:

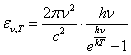                                                  (1).

From (1) we see, what  = 0 at  = 0 and at .

From here it is possible to draw a conclusion, that the Planck formula is erratic and does not correspond to experiment. It can be seen with ones own eyes on absence of visible radiation from a body heated, for example up to 550⁰С, which one seems dark brown only in darkness, though the Planck formula allows gentle radiation further in visible area. For example, the counting under the formula (1) gives a radiated power for this temperature in the field of 7000 A,  = 0.5156×10^-13 ergs/cm², and in the field of a maximum visibility 5600 A,  = 1.964×10^-16 ergs/cm². The radiated power decreases in 262 times, but also the visibility is augmented with 0.0041 up to 0.995 i.e. in 242 times (N.I. Koshkin, M.G. Shirkevich. The reference book on elementary physics. Moscow, 1962, page 169). Accordingly, is erratic the distribution of a Bose-Einstein on which one Planck formula also is grounded. The experiments demonstrate, that the heat radiation always has rather clear short-wave boundary and more vigorous photons does not beam.

Distribution function of bosons, fermions and «boltzmons» (if so) in quantum and classic statisticses it is possible to record by one expression (B.M. Yavorsky, A.A. Detlaf. The reference book on physics, «Science», Мoscow, 1964, page 215):

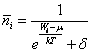                                                            (2),

where:  - average of particles in the given condition, W_i - energy of this condition, - chemical potential dependent from state parameters and structure of a homogeneous system, but not dependent from its mass, k - Boltzmann constant, T - absolute temperature, =0 for distribution of a Maxwell-Boltzmann («boltzmons») - classic particles, =-1 for distribution of a Bose-Einstein (bosons), = +1 for distribution a Fermi-Dirac (fermions). From (2) it is visible, that the difference between statisticses is appreciable only at , i.e. for a case of a zero-point energy of a particle, that in the nature does not happen. If the energy of a particle in 2-3 times exceeds a thermal energy, all particles are transformed in classic, since unit in a denominator (2) can be neglected. In chapter 23.1 is shown, that the energy is necessary for formation of a photon at given temperature:

                                                               (3).

Thus the value  in (2) can be neglected. Here it is necessary to mark, that the orthodoxes manage to apply statistics of fermions (Pauli's exclusion principle) even to atomic electrons, the energy which exceeds one in hundreds time a thermal energy, therefore they obey to classic statistics. Thus, at some excess of energy of bosons and fermions above a thermal energy, they lose all regalia, with which one they were awarded by orthodoxes and are transformed in customary plebeians of mechanics of a Newton. On the basis of set up it is possible to assert, that the Planck formula for heat radiation is successful adjustment under the answer by means of mathematical manipulations not having of clear physical sense.

New physics has shown, that the photons move on a screw trajectory with equal translational and tangential velocity C. Therefore separate photon in a direction from a beaming body bears translational energy:

                                                                 (4).          

Then is apparent, that the radiant capacity of an ideal black body will be peer to translational energy of a photon referred to a sectional area S of its screw trajectory:

                                                                  (5).

Sectional area of a trajectory:

                                                                  (6),

where r - radius of a screw trajectory photon. It we shall discover from the fact of an identical angular momentum for microparticles:

                                                                   (7)

established by a de Broglie formula:

                                                                   (8).

From (6), (7) and (8) we shall discover:

                                                                    (9).

The formula (9) we shall express through frequency of a photon and we shall substitute in (5):

                                                             (10).

We have received the formula Rayleigh-Jeans for emittance of a black body, where instead of «thermal» energy of a photon there is its own energy. This formula requires an additional factor reducing a radiation energy up to zero point for vigorous photons, since the unlimited energy of a photon physically is impossible.

To receive a Planck formula from (10), it is necessary this equation to multiply on distribution of Bose-Einstein, but we it to make shall not be from following reasons. The large lack almost of all theories of a modern physics in which somehow allowed some statistical distribution of parameters is consist in «perpetuities». For example, the molecule of gas can gain infinite speed or energy, though it cannot to itself be presented as outcome of impact with other molecules. It is quite possible, that the molecule as a result of several series impacts with the neighbours has gained some exuberant energy in comparison with mean energy (such energy it can not gain at the expense of simultaneous impact with the several neighbours, since the simultaneous impact is impossible). But under the known theories this energy can in tens and hundreds time exceed mean, that is impossible. On the same official notions of Hydrogenium can step-by-step be transformed into deuterium etc. However in practice we is not observed of very vigorous «tails» of any distribution. Heated up to 550 ⁰С the body does not release ultra-violet, x-ray and gamma rays, though basically Planck formula allows it to do. Here can object, that the calculation on a Planck formula for this case gives vanishingly small a radiation energy in short-wave range, but it not the evidence of a validity of the formula. Let us suppose is beamed one X-ray quantum for hundred years - business you see basically. Besides in heat radiation heat motion of atoms transfers them in an exited state with the subsequent radiation of photons, therefore record of a kind  basically is incorrect. How many atom has received thermal energies, so much has released as a photon. By receiving some exuberant energy the atom can be saved of it by several photons, therefore their common energy  Is always proportional .

Any so-called «electromagnetic radiation» is a flow of photons. The heat radiation of a body is connected to random heat motion of atoms of this body therefore does not depend on a chemical composition. At once there is a problem on the mechanism of transfer of atoms in an exited state with the subsequent radiation of photons of heat radiation. On notions of official physics the energy levels of atoms are inspissated far from a ground state. To throw an electron even on the second energy level it is necessary to expend energy a several electronvolt. At the same time mean energy of heat motion makes only 0.025 eV at room temperature. Therefore excitation of atoms at the expense of their heat motion is impossible from the point of view of official physics. The references to vigorous particles «of a lengthy tail» do not decide this problem since as a matter of fact «tail» short. Any statistical distribution of particles in official physics guesses presence of particles possessing, basically, infinite energy. But the nature does not tolerates zero points and infinities. If there were such particles, the spontaneous ionization of atoms would be watched, since if the particles of «tail» are capable to throw electrons on high energy levels, it is necessary to add not enough energy to ionize atom. How many we did not wait for appearance of a photon of a visible light in a radiation spectrum of a black body at room temperature, we it never awaited, though the Planck formula enables appearance of any photons. All this speaks that any distributions of particles in a modern physics are erratic. Thus, the modern physics can not sensible to explain appearance of heat radiation.

I result detailed analysis of reasons of appearance of heat radiation from the point of view of new physics. New physics considers, that the energy levels of atom are inspissated near to a ground state, therefore to transfer atom in an exited state any gentle effect on it is capable. As a result of impacts of atoms with each other they appear in a miscellaneous degree of excitation from zero point up some maximum value. This maximum value is determined by that the thermal energy of particles grows linearly with temperature, and the energy indispensable for throw of an electron on more a high level grows in quadratic relation. Therefore at given temperature there is such energy level on which one it is impossible to throw an electron by means of a thermal energy. It determines maximum energy of photons of heat radiation.

Let's consider an extreme case of maximum excitation of atoms. Let's presume, that two identical atoms with identical energy have tested head-on impact. Apparently, that after that they «will stay». Where their kinetic energy has got to? It is clear, that it has spended on excitation of these atoms. And it is optional was arranged only on two equal parts. Energy can bodily proceed to one of them. It depends on a mutual disposition of outside electrons at the moment of impact.

On the Arrhenius, the concentration excited atom C is peer:

                                                                   (11),

where: C₀ - common concentration of atoms, E - activation energy of process of excitation of atom.

Apparently, that the activation energy of excitation of atom in accuracy is peer to energy of a photon (photons) radiated behind excitation, since the atoms receive or return excitation by strictly definite portions.

                                                                     (12).

Let's substitute (12) in (11):

                                                                  (13).

The emission intensity will be directly proportional concentration excited atom and is inversely proportional concentration of nonexcited atoms:

                                                                (14),

where: K - proportion factor equal (10).

By substituting (13) in (14), after some transformations we shall receive:

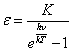                                                                   (15).

By substituting (15) in (10) we shall receive the formula in accuracy coincident with a Planck formula (1), but having absolutely other sense. This example once again confirms a surprising phenomenon in science, when from opposite initial hypotheses it is possible to receive the same outcome. Simultaneously it once again demonstrates, that the obtaining of outcome, affirmed experiments, is not endorsement of rightness of initial hypotheses.

Degradation of oscillators.

Let's consider an insulated system in which one placed body with temperature T.

It is represented apparent, that at given temperature there will be practically one oscillator, which one has gained maximum energy. What will happen with this energy? Two paths with identical outcome here are possible. The oscillator in 10^-8 seconds or at once will radiate a photon with this energy and will transmit to its neighbours. Or is more likely, that it will exchange energy on a several more long-wave photons as a result of a successive transition on the ground level. That most will make also any of its neighbours received such vigorous photon. As a result of a similar degradation of an oscillator its maximum energy will be scattered. That expects and following oscillator acquired maximum energy etc. As a result of a degradation of oscillators the system will be stuffed by photons possessing all time by decreasing energy, and the maximum energy of the most vigorous oscillator also step-by-step will decrease. The process of a degradation is possible to compare with bursting of bubbles of the decreasing sizes through everyone 10^-8 seconds. Ultimately temperature of a body will become to close absolute zero of temperature, and space of an insulated system will be filled by «relict» photons. In this sense «thermal death» by the Universe, as insulated system (so thinks new physics) as a result of equalization of temperatures of its members there is no in any a matching with described «absolute thermal death» the Universe. But the below mentioned calculations demonstrate, that the similar horror does not threaten to us. The Universe long before «absolute thermal death» will finish the next cycle of oscillations and all will begin anew. It is interesting to count up, how many time is necessary to wait for «absolute thermal death» of a heated body of mass 1 mol matters? In this mass is contained 6.02×10²³ potential oscillators. Provided that each of them loses the energy in 10^-8 seconds, all energy they will lose for 6.02×10¹⁵ seconds or 191 million years. Therefore alone, while, evidence of a degradation of oscillators the relict radiation of space is.

13.1. Some particulars of an electron orbital motion

The velocity of an electron on an orbit of the Bohr is peer 2.1877×10⁸ cm/sec. On any excited level the electron on the average is 10^-8 sec. For this time it transits on an orbit more than 2 cm or does about 66 millions revolutions around of a nucleus. At each revolution the electron has chance to pass on higher or more low level, including at absorption by atom of a thermal radiation. Therefore except for Doppler expansion of spectral lines at the expense of heat motion of atoms there will be an expansion of lines at the expense of "jar" of an electron on any of time orbits, which one represent a composition from numerous close of arranged sublevels, on which one the electron skips at orbital motion. At transition of an electron to more low level it as a matter of fact from a casual sublevel more the high level transfers on a casual sublevel more low level. The miscellaneous atoms radiate thus photons by close each other, but not equal energy, that gives in expansion of a spectral line in some correspondence with a radiation spectrum of an ideal black body.

As the potential energy of repulsion depends on distance from nucleus, stronger than the potential energy of an attraction, at transition of an electron from one orbit on another because of an electron inertia an electron oscillates about a stable orbit. At removal from a nucleus the repulsive force decreases also sharply attractive force returns an electron on an orbit, and at approach to a nucleus a repulsive force is incremented sharply.

13.1.1. Birth of photons at formation of hydrogen atom.

The theory of atom of the Bohr envisages aliquot value of angular momentum of an electron on steady orbit:

                                                                (13.1.1.1).

The wave mechanics too is convinced a capability of aliquot value of electron angular momentum. In this occasion new physics has following opposition.

Law of conservation of angular momentum one of the fundamental laws of the nature. Neither for the Bohr, nor in a quantum mechanics is not illustrated, whence for an electron the infinite number of moments arises, as the quantum number n theoretically can be infinite. Whence there are these moments? Below is shown, that for impart to a particle of angular momentum it is necessary to expend definite energy. Where there is a source of this energy in official physics? If this source do not indicate, it means direct violation of one of the fundamental laws, since in this case angular momentum arises from nowhere.

In chapter 13 is shown, that a reserve for birth of photons at formation of hydrogen atom is the kinetic energy E_c, bound with radial component motions of an electron V_c in relation to a nucleus:

                                                                 (13.1.1.2).

At radiation of photons the radial velocity of an electron decreases in an integer of time in relation to maximum radial velocity, which one is reached apart of radius of orbit of the Bohr and becomes of an equal orbital velocity V₀ of an electron on this orbit (formula (13.13)):

                                                                 (13.1.1.3),

where N - number of radiated photons. By substituting (13.1.1.3) in (13.1.1.2), we shall receive:

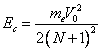                                                             (13.1.1.4).

The formula (13.1.1.4) demonstrates, that with each radiated photon kinetic energy, bound with radial velocity of an electron, decreases fourfold. For example, at radiation of the first photon E_c becomes equal: 13.605¤4 = 3.4 eV, and energy 10.2 eV takes off a photon. At N this kinetic energy is spent completely for formation of photons and there is only kinetic energy, bound with a tangential velocity of an electron on a circular orbit :

                                                                (13.1.1.5),

where V₀ - orbital velocity of an electron in a ground state.

To create a photon, it is necessary to impart to it angular momentum on a screw trajectory and to expend the same energy for impart translational motion on this trajectory. It is known, that the kinetic energy of a rotated body E_rot is determined by the formula:

                                                              (13.1.1.6),

where: J - moment of inertia of a body, - angular rotating speed.

In (13.1.1.6) we shall decrypt in applying to a photon a moment of inertia it on a screw trajectory and connection of peripheral speed at rotation on an coil (equal speed of light) with radius of an coil:

                                                          (13.1.1.7),

where: m_ph - mass of a photon, c - speed of light, r_c - radius of an coil of a screw trajectory of a photon. Allowing, that the angular momentum of a photon is peer , and =2, where  - frequency of the revolution of a photon on a screw trajectory, the formula (13.1.1.7) to become:

                                                             (13.1.1.8).

Apparently, that for translational motion it is necessary to a photon to give the same energy, since tangential and forward speed on a screw trajectory are peer. Then energy of a photon:

                                                              (13.1.1.9).

Thus, we have defined a power source for originating photons, and have found a principle of consumption of this energy.

Official physics is afraid directly to state, that the motion of an electron in atom is orbital motion. As soon as it recognizes it, automatically falls under wheels of the own machine, by which one it has crushed the theory of the Bohr. At the same time without any confusion considers a spin-orbit interaction, though on its notions of orbital motion of an electron should result in to continuous energy loss at the expense of radiation. Electron orbits in atom, both under the theory of the Bohr, and on a wave mechanics circumferential, i.e. radial component orbital velocities misses and there is no incentive for an electron to come nearer to a nucleus. It is necessary to attract the far-fetched interplay with vacuum to explain instability of exited states of atom. For many reasons official physics is under the necessity to refuse visual notions. But just the visual notions are the basis of logic, including the physical logic. The waiving them is equivalent to analysis of a surrounding world with the knotted eyes.

13.1.2. Trajectories of electrons in atoms

Let's try to analyze this problem in logical sequence. Now it is no doubt, that the atoms contain positively charged nucleuses and negatively charged electrons. The theorem Irnshow asserts, that the stable state of a system of the stationary arranged charged particles is impossible. From here follows, that the atoms represent dynamic systems. Here we at once meet a paradox.

At any conceivable trajectory inside atom, the part of this trajectory, on necessity, should be accompanied by negative acceleration at which one atom beams photons with which one of a system the exuberant energy abandon, stored on a segment of positive acceleration. Thus, any atom should continuously lose energy and their existence will become impossible, contrary to a nude fact. Within the framework of official notions about radiation of atoms to permit this paradox it is impossible. If to address to notions of a quantum mechanics, any repositioning of an electron x is accompanied by change of its impulse P pursuant to an indeterminacy principle of Heisenberg. On these notions occurrence of acceleration at motion of an electron is in the nature of things, therefore quantum mechanics is not compatible to stability of atoms. What should be a trajectory of an electron in atom, that there were no accelerations at its motion? The official science does not give the answer to this problem. The answer is given only by new physics - trajectories of electrons should be circumferential. Only on such trajectory there no accelerations and bound with them radiation. Here at once is audible growl of the professors, which one urge the students to decide a «simple» problem of energy loss by an electron at the expense of «electromagnetic» radiation under operating of «centripetal acceleration». However, scientists do not perceive motion of a body on a circumference, that is shown in chapter 1 and 1.1. It is necessary to analyze compatibility of the theory of the Maxwell of electromagnetic radiation with stability of atoms. Any electron of atom at motion creates a variable electrical field, which one under the theory of the Maxwell excites originating a magnetic field. This process is accompanied by electromagnetic radiation and irreciprocal energy loss. Thus, the theory of the Maxwell is error, that with all evidence confirms stability of atoms. It is necessary an alone capability to ensure this stability - uniform motion of electrons on circular orbits on which one radiation misses.

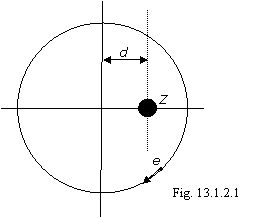
On a figure 13.1.2.1 the electron of multielectronic atom and its circular orbit is shown.

Any electron in atom slips on a bottom of a potential well and at this even circular motion the attractive force of an electron to a nucleus of atom is always peer and inversely is directed to a general repulsive force from all remaining electrons, therefore nucleus of atom will be located from center of a circular trajectory of an electron on some equilibrium spacing interval d. From a figure 13.1.2.1 it is visible, that the attractive force of an electron to a nucleus of atom on orbit varies sinusoidal. In precisely the same way should vary and general repulsive force from other electrons. This condition demands stringent synchronization of motion of all electrons of atom.

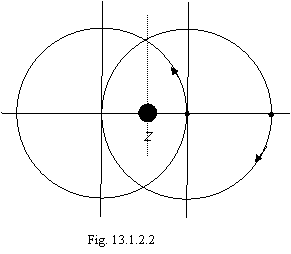
On a figure 13.1.2.2 two electrons helium-like of atom are shown. For one electron the center of orbit coincides with position of a nucleus, but the interaction of electrons displaces their centers of orbits in the miscellaneous sides.

The author hopes, that the enthusiasts of engine calculations and computer simulation in due course will receive precise delineations of all atoms.

13.2. As atoms are forms

If the electron comes nearer to a "bare" nucleus, having in perpetuity zero velocity, its velocity is incremented up to value "of the second solar escape velocity", the trajectory becomes parabolic, and it again leaves in perpetuity. If the initial velocity was not zero, the trajectory will be hyperbolic. From this point of view an electron capture with formation of atom the same as also capture of space bodies are impossible. This corollary of the law of conservation of energy. That the capture has taken place, even the small power loss by an electron is indispensable. The universal power loss in a similar case, both for space bodies, and for an electron is identical: transmission of a part of an impulse to all system as a whole. For space bodies it is an alone expedient of capture and further evolution of an orbit. For an electron there is an opportunity to lose exuberant energy with a radiated photon. But the radiation does not cancel power loss by transmission of a part of an impulse, which one it is impossible to avoid. Let's enter concept of excess velocity of an electron. The excess velocity is a difference between velocity in pericentre of an elliptic orbit V_p and velocity on a circular orbit V₀ or orbit with a smaller eccentricity V_p2:

V_exc = V_p – V₀ или V_exc = V_p1 – V_p2                          (13.2.1)

Angular momentum of an electron:

и                                 (13.2.2).

From (13.2.2):

                                            (13.2.3).

In (13.2.3) we shall substitute (13.2.1) and known expression for distance up to pericentre (13.19). After small transformation we shall discover expression for an eccentricity of orbit:

                                             (13.2.4).

If the electron had initial velocity peer to zero point, it before capture will gain excess velocity V₀, the eccentricity is peer 1, a trajectory parabolic and the capture is impossible. Radiation of a photon and the transition to more low-altitude orbit though is possible, but is unlikely, since the electron is near to a nucleus only 0.5×10^-16 sec. However as a result of interaction with a nucleus the electron has gained some impulse, what its part will transmit to a nucleus, we now find out. On a law of conservation of impulse:

mV_exc = MV_M – mV_p                                        (13.2.5),

where MV_M - impulse received by a nucleus mV_p - stayed "exuberant" impulse of an electron.

The energy balance:

                                      (13.2.6).

Solving jointly (13.2.5) and (13.2.6), we shall discover:

                                          (13.2.7).

Thus, the electron has lost a small part of the energy. But it is quite enough of it that the parabolic trajectory was turn into elliptic, i.e. there was an capture. For second and subsequent revolutions around of a nucleus:

                                       (13.2.8),

where N - speed around of a nucleus. By substituting (13.2.4) in (13.2.8) we shall discover, as the eccentricity of orbit varies:

                                          (13.2.9).

The calculation on (13.2.9) gives following values of a eccentricity after the first revolution around of a nucleus: for hydrogen e_H = 0.99891, for uranium e_U = 0.9999953. Despite of a huge difference between masses of uranium nucleus and electron transmitted to a nucleus an impulse quite is appreciable.

The third Kepler's Law can be conversed to a view:

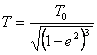                                          (13.2.10),

where T - period of rotation on an elliptic orbit, T₀ - period of rotation on a circular orbit.

The calculation on (13.2.10) with the registration (13.2.9) gives a period of rotation on the first revolution around of a nucleus for hydrogen 1.49×10^-12 sec, and for uranium 0.622×10^-12 sec. Also it is easy to count up, how much energy will be lost by an electron after the first revolution: W = 13.6(1-e²) = 0.03 eV. It is interesting to count up, how many revolutions around of a nucleus should be given by an electron, that from an orbit Lyman to pass on an orbit Balmer. For this purpose in (13.2.9) we shall substitute indispensable numerals: 0.5=0.99891^N whence N = 636 revolutions. As much of sublevels will be between these two levels. The density of sublevels is incremented on more low-altitude orbits since the impulse, transmitted to a nucleus, with each revolution decreases. The presence of numerous sublevels in energy levels of atom causes an continuous spectrum after a limit of any spectral series. Explanations of official physics, that the continuous spectrum after a limit of a spectral series is stipulated by that the electron before capture has some energy, are erroneous since such electron can not be captured, will not lose yet this exuberant energy. Besides from a point of view of official physics it is not clear, how the electron in atom in some cases can appear between energy levels. Now it is necessary to answer a problem: why at transition of an electron from one level on another the photons are radiated, and at transition with each revolution from one sublevel on another we not visuals photons? At transition on levels the excess velocity of an electron decreases in an integer of time, that causes considerable change of energy of an electron. 

If the atom "has missed" to radiate a photon, while the electron was at a given level, it prolongs to be lowered on sublevels, the not following opportunity will not appear yet to radiate a photon. At transition on each revolution from one sublevel on another (to skip through them an electron can not) the energy of an electron varies lightly, that is shown above, therefore it as a matter of fact transfers non-radiating in energy of heat motion of atom in the whole. Photons in this case are radiated mediate because of a thermal exchange of radiation under the law of the Planck.

In conclusion of this section it is necessary to mark, that the author can not accept many concepts of a modern physics, them to not number, here only some: a centripetal acceleration, S-electrons, spin, Pauli's exclusion principle, indeterminacy principle of the Heisenberg, tunnel effect, laws of a microcosm, quantum mechanics, independence of apparent velocity of light of a motion of the spectator, contortion of space, deceleration of a course of time, black holes etc. If fully to shock this or that branch of physics, these concepts burst, as the soap bubbles, but not on one, and on a chain, which they are bound. Watching this picture, involuntarily it would be desirable to supplement the J.J. Thomson by that by most relevant for science by service is not only introduction of new ideas, but also comprehension of the perversity old.

13.3. Atom of hydrogen

Wave quantum mechanics. On notions of official physics, the potential well for an electron near to a proton has a view shown on a figure 13.3.1 (to the left of proton a picture is symmetrical).

Pay attention to that the walls of a pit in each point have miscellaneous curvature and are not perpendicular anywhere to any level of energy. In three-dimensional space the potential well will look as an orb with a proton at centre for a certain potential energy. For other level of energy radius of an orb will be more or less depending on a standing of this level. What view will in space more than three-dimensional know only perverters of sensible physical sense.

For this problem again will utillize a stationary Schrodinger equation, that means, that in space between a wall of a potential well and proton the system of standing spherical waves should be formed. Thus, in atom of hydrogen each chunk of the particle, sliced on a part, swollen as a bubble and these bubbles are inserted each other. But because of curvature of walls of a pit the reflected wave can not be spread in precision on a direction of an incident wave, i.e. the formation of standing waves anywhere is impossible. The formation of standing waves in official physics also prohibits a principle of indeterminacy of the Heisenberg, since at reflection from a wall of a potential well the position of a particle is known precisely, but neither direction of an impulse of a particle, nor its value it is impossible to point. It concerns not only problem concerning to atom of hydrogen, but also all problems, the solutions which one are grounded on a Schrodinger equation. On this warrant it is possible to state, that this equation is useless because it could not be applied. It is confirmed also by results of applying of a Schrodinger equation to atom of hydrogen. Thus the levels of energies condensed to a state of a mobile electron are gained.

There is one more principled difficulty for a wave quantum mechanics, which one is forced always to be address to standing waves to remain quantum. In a loop of a standing wave the slice of a charged particle oscillates across a wave and represents an electric dipole, radiating electromagnetic waves, the radiation which one is directional along a wave. Therefore energy of a particle should promptly be diffused, and the radiation spectrum will be continuous. Official physics puts from an ill head on healthy, shifting this principled difficulty on circular motion of an electron around of a nucleus, comparing this motion with an electric dipole. It is possible to point and one more principled difficulty for a wave quantum mechanics and on it enumeration of difficulties we shall conclude, for funeral already will suffice. Applying for a viewed problem the stationary equation, naturally, is gained also the stationary solutions - stable levels of energy in atom of hydrogen. But actually ground state is stable only, at remaining levels of energy the electron is not impeded more than 10^-8 seconds. Therefore it is necessary to attract one more "invention" of orthodox physics - "virtual particles of empty space", that how to explain stability of energy levels.

Classic mechanics. In chapter 2 the formula for radius of an orbit of an electron in a hydrogen-like atom (2.3) and electron-binding energy with a nucleus (2.4) is received on the basis of only classic notions not attracting quantumness in any view.

Corpuscular quantum mechanics. In a start of this chapter enough detail this problem is developed. Therefore here it is better to be stopped on some circumstances of the theory of atom. For this purpose we shall take advantage of the data of table 13.1 and figure 13.2. It is as a matter of convenience, the part of a figure 13.2 in the simplified view is shown on a figure 13.3.2.

Ground state of an electron on a circular orbit of the Bohr (4), shown a dotted line. We visuals, that the electron at a motion on elliptic orbits oscillates concerning an orbit of the Bohr, coming nearer to a proton (in pericentre), being deleted from it (in an apocenter). Thus, the electron represents an oscillator with equilibrium point conterminous to an intersection point to an orbit of the Bohr (of the points A and B). Here it has maximal radial velocity and maximal kinetic energy, bound with this velocity. In points of pericentre and apocenter of an orbit the radial velocity of an electron is peer to zero point and it has a maximal potential energy in these points (concerning an orbit of the Bohr). Apparently, that if the electron in a point A will have a kinetic energy more than 13.6 eV, it will be moves on a hyperbolic orbit through a point A, in pericentre between a point C and proton and through a point B. On a braking phase AC to be captured, the electron is obliged to have time to radiate a photon with energy even hardly more its exuberant energy relatively 13.6 eV to pass in a point B to an elliptic orbit. The provisional time diagram of change of a potential energy at oscillations of an electron concerning an orbit of the Bohr is shown on a figure 13.3.3 for the first three values of a quantum number.

Let's accept a beginning of timing from the moment of passage by an electron of a point A of intersection of orbits. At n=1 first half-period of oscillations of an electron will be completed rather promptly, since the tangential velocity of a motion of an electron in pericentre is maximum. In a point of pericentre the potential energy of an electron is maximal and numerically is peer to ionization energy. At intersection orbit of the Bohr (point B) the potential energy of an electron (concerning a ground state) accepted zero value. The extremity of the second half-period of oscillations we not awaited, since on a parabolic orbit the electron is deleted on perpetuity and its potential energy concerning a ground state again becomes of an equal ionization energy, and kinetic accepts zero value. At increase of a quantum number the first half-period of oscillations slightly is incremented, and the second half-period rather sharply is reduced, the oscillations amplitude decreases, the oscillations more and more come nearer to simple harmonic motions, and shape of an orbit to a circle. At n the oscillations fade and together with them the radiation fades. The electron takes a ground state on an orbit of the Bohr. On hyperbolic trajectories the potential energy of an electron in pericentre always is more than a level E₀ (fig. 13.3.3).

To find dependence of a potential energy of an oscillator in atom of hydrogen from value of a quantum number, we shall take advantage of the formulas (2.2), (2.3) and (2.4) chapter 2. In these formulas we shall substitute the formulas for distance from a nucleus in pericentre and apocenter depending on a quantum number from table 13.1:

                                          (13.3.1)

for pericentre and:

                                          (13.3.2)

for an apocenter.

Substituting (13.3.1) in (2.2) with the registration (2.3) and (2.4), we shall receive a potential energy in pericentre:

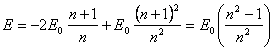                      (13.3.3).

To find a potential energy of an oscillator concerning its equilibrium state (orbit of the Bohr), it is necessary from its blanket potential energy in pericentre on (13.3.3) to subtract a potential energy in a stationary state E₀:

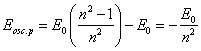                            (13.3.4).

As well as it was necessary to expect, the potential energy of an oscillator is negative in matching with an orbit of the Bohr, and its numerical value coincides the theory of atom of new physics.

Substituting (13.3.2) by a similar way we shall discover a potential energy of an oscillator concerning an orbit of the Bohr in an apocenter:

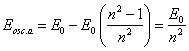                               (13.3.5).

Thus, we have found out the physical reason of radiation of atom. Besides from a figure 13.3.3 it is visible, that at transitions from one orbits on another the electric dipole changes in strong degree oscillations amplitude and in a small degree an oscillation frequency. The frequency of a half-period, bound with pericentre always is little bit higher than frequency of a half-period, bound with an apocenter. Therefore electron in points of an orbit A and B will radiate photons with little bit distinguished energy (doublets of spectral lines). Especially this difference is appreciable at small values n.

Scoring more thin effects, it is necessary to pay attention that the electron at orbital motion is "dragged” behind itself and proton, though its mass almost in 2000 times more. Besides at the expense of electron inertia its orbit is gyrated in the side of a motion of an electron. The velocity of this gyration is determined only by eccentricity of orbit of an electron and value of a major axis. That this deduction was clearer, we are address to a figure 13.3.4.

At a motion of an electron from an apocenter 2 to a point A, its radial velocity is incremented from zero point up to a maximum, and after passage of a point A its radial velocity sharply drops, since in a point 1 pericentre it again should accept zero value. The electron inertia gives that the intersection point with an orbit of the Bohr displaces counter-clockwise on value, proportional acceleration of an electron, which one depends on an eccentricity of orbit and semimajor axis (point A'). The position of pericentre too displaces (point 1'). The second intersection point with an orbit of the Bohr (point B') for the same reason displaces also. In result and the position of an apocenter appears in the other place (point 2'). The same reasoning are valid and for gyration of elliptic orbits of planets.

The indispensable requirements for radiation of photons. The main requirement for radiation by free or bound electrically charged particles - negative acceleration of electric charge. In a bound state (in atom or molecule) except for negative acceleration should be fulfilled the requirement of radiation only integers of photons (radial velocity can decrease only in an integer of time of comparatively parabolic velocity). Therefore on an elliptic orbit, on which one the indicated requirement is not fulfilled (for example, between energy levels), the oscillator though oscillates, but nothing radiates. On such orbit it is forced to lose a part of energy at each revolution around of a nucleus at the expense of transmission to atom in the whole part of the impulse until the indicated requirement will be carried out.

Energy of connection in a ground state from the formulas (2.3) and (2.4):

                                        (13.3.6),

where r₀ - radius of an orbit of the Bohr. The formula (13.3.6) will be valid and for electron-binding energy in a position of pericentre r_p and apocenter r_a. Apparently, that the potential energy concerning an orbit of the Bohr for pericentre should be peer to a potential energy concerning an orbit of the Bohr for an apocenter, that the law of conservation of energy in an antiradiation condition was fulfilled:

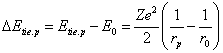                            (13.3.7),

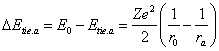                            (13.3.8).

Let's designate r_p=r₀P and r_a=r₀A, where P and A - share of pericentre and apocenter from radius of the Bohr. Allowing these designations and equating (13.3.7) and (13.3.8), we shall discover:

                                             (13.3.9).

The equation (13.3.9) has uncountable set of the solutions, and all of them meet the requirement maintenances of energy. Now it is necessary to receive expressions P and A through a quantum number n. By it we from uncountable set of the solutions (13.3.9) shall select only «integer» solutions that physically mean the requirement of a wholeness of a radiated photon. Apparently, that at n=1 A=, and from (13.3.9) P=1/2. At n= from (13.3.9) P=A=1. It is uneasy to guess, that such property has the functions at r₀ of expressions (13.3.1) and (13.3.2). Thus, both at a motion to a ground state, and at a motion to a state of an atomic ionization the electron beforehand "knows" parameters of all orbits, on which one it is authorized to it to radiate photons. On all remaining orbits the electron is an oscillator, but the radiation is forbidden. On an orbit of the Bohr the radiation is authorized, but on it the electron does not oscillate - radiation is not present. Too concerns a motion of an electron on an isopotential orbit of any shape, for example, in molecules. On such orbits the electron is not an oscillator.

In connection with enunciated, some words are necessary for telling about multielectronic atoms. In a ground state of these atoms the electrons motion on circular orbits is impossible because of influence of electrons against each other. Therefore electrons should be moves though is self-consistent, but on ellipsoidal orbits, on which one the requirement of a wholeness of radiated photons is not fulfilled, therefore radiation is not present. They also can be moves on an isopotential surface of any shape, on which one also radiation is forbidden, as the potential energy of an electron remains to a stationary value. Besides the orbits of electrons should be symmetrical concerning a nucleus of atom. In this case change of an orbit of an electron at the expense of transmission of a part of its impulse to atom as a whole is impossible, since the vector addition of impulses received from all electrons should give zero point. Motion on a "forbidden" or isopotential orbit and impossibility of its self-maintained change ensure existence and stability of all present atoms.

13.4. The electron with a total energy is more than zero point in atom of hydrogen

Radius of a screw trajectory of an electron is bound to its velocity by a relation:

                                                (13.4.1),

where V - forward speed of an electron, =1.1576 cm²/sec (see chapter 2). For a mobile electron a kinetic energy of headway of a particle:

                                          (13.4.2).

By substituting (13.4.2) in (13.4.1), we shall discover connection of radius of a screw trajectory with a kinetic energy of headway:

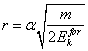                                         (13.4.3).

As it is visible, the formula (13.4.3) does not contradict physical sense. Substituting in it the relevant numerical values and E_k=13.6 eV (1 eV = 1.602×10^-12 ergs), we shall receive value of radius to equal radius of an orbit of the Bohr. It means that if the total energy of an electron (in perpetuity) is more than zero point, radius of its screw trajectory always is less than radius of an orbit of the Bohr. In connection with enunciated, the hyperbolic orbits of an electron around of a proton are impossible in their classic comprehension. The trajectory of an electron with a total energy is more than zero point near to a proton is shown on a figure 13.4.1.

Designations on a figure 13.4.1.

1. Trajectory of an electron in perpetuity having a kinetic energy 13.6 eV. Radius of a screw trajectory is peer to radius of an orbit of the Bohr. At approach to orbit of the Bohr the energy of an electron will increase up to 27.2 eV.

2. Orbit of the Bohr.

3. One of elliptic orbits after a braking radiation of a photon with energy is more 13.6 eV.

4. Proton.

5. Parabolic orbit at a braking radiation of a photon with energy equal 13.6 eV.

6. The prolongation of a trajectory of an electron, if a braking radiation missed. At removal on perpetuity the electron loses 13.6 eV from 27.2 eV and its energy again becomes equal 13.6 eV.

Summing up audit of bases of a modern quantum mechanics, it is possible confidently to state, that these fundamentals do not withstand criticism and should be exchanged by new notions. Already it is clear, that the orthodoxes can not put forward the argued oppositions in protection of an official quantum mechanics or in refutation of new physics, therefore further events are uneasy for foreseeing. New physics in the beginning waits an ignoring, then billingsgate and, at last, blanket recognizing in accordance with extinction of the fans of official physics.

13.5. Rydberg atoms

More in detail about rydberg atoms it is possible to read, for example, in Soros Educational Journal 1998, № 4, page 64. They represent macro atoms on the size (up to 0.02 mms) located in a condition of high excitation on the verge of ionization with a main quantum number about 1000 on presentations of official physics. Accordingly, radius of such atom in 10⁶ times more radius of a normal atom. The capability of creation and existence of rydberg atoms allows, at last, finally to be disassembled in differences of official and new physics on a constitution of atoms.

1. At first we shall be disassembled with official notions about radiation and occluding of energy by atom. They outgo from a capability of an aliquot angular momentum of an electron on «orbit»:

                                                          (13.5.1),

where m₀ - no relativistic electronic mass, V - its orbital velocity, r - orbit radius, n - integer,  - constant of the Planck. Apparently, that (13.5.1) is direct violation of law of preservation of angular momentum so long as we shall not find out, this aliquot increase of angular momentum of an electron whence arises. For this purpose it is necessary to consider angular momentum of an electron on orbit at n = 1 same, as well as angular momentum of a photon, i.e. . I shall remind to the reader, that the law of conservation of angular momentum requires, that the angular momentum of a mobile electron also should be peer . The theory of circular orbits of an electron is set up in chapter 2. Let's consider the formula (2.3) for radius of a circular orbit and (2.4) for electron-binding energy on a circular orbit:

                                                            (13.5.2),

where:

 = Vr                                                                  (13.5.3)

                                                            (13.5.4).

As an electron in atom always not relativistic (see chapter 7.2.1), the repetition factor of electron angular momentum in atom is connected to repetition factor of product Vr:

                                                                 (13.5.5).

At n = 1 electron is in a ground state on orbit of the Bohr (in atom of hydrogen). To transfer it in an exited state with Vr = 2 it is necessary, that the atom has occluded the applicable photon and has transmitted energy and impulse of this photon to an electron. Thus the electron again will be on a circular orbit, radius by which one in 4 times more radius of a ground state. Any circular orbit is stationary, being on it an electron anything to beam can not. That there was an energy loss, some exuberant energy, distorting circular orbit in elliptical (see chapter 13) is indispensable. Further again is necessary occluding a photon and transfer of an electron in a condition with Vr = 3 etc. Thus, the transition of an electron from one energy level on another from the point of view of official physics is possible only at series occluding of photons, and jumping through one or greater number of levels it is impossible, if there is no simultaneous occluding of several photons. Outcomes of the official theory we shall receive, by substituting (13.5.5) in (13.5.2) and (13.5.4):

                                                                     (13.5.6),

                                                                  (13.5.7)

whence it is visible, what on considered notions of levels of energy are inspissated at nearing to an ionization energy of atom n, E0. At n = 1 electron is on orbit of the Bohr. The surprising commonality macro and micro cosmos is confirmed by that circumstance, that in the coerced analysis of official outcomes radius of a circular orbit of an electron is proportional to a square of a quantum number n, and the speed of an electron on any circular orbit in an integer of time (n) is less than speed on orbit of the Bohr. In chapters 20 and 21 the precisely same conclusion is made concerning quantum condition of planets and their satellites (see figure 21.4). From above set up clear, that rydberg the atoms can be received only at continuous occluding of photons with continuously decreasing energy down to boundary of ionization. Electron-binding energy in such atoms is insignificant; therefore any impact with extraneous particles results in ionization of rydberg atoms. If impacts to avoid, rydberg atoms metastable, that confirms an antiradiation condition at motion of a charge on a circumference at absence of motion in a radial direction.

2. The notions of new physics concerning radiation and occluding of energy by atom are particularized in chapter 13 and in the subsequent chapters. From the point of view of new physics there is only one circular orbit of the Bohr, therefore electron on it does not beam. All remaining orbits elliptical, for which one is present radial component running speeds being a reserve for radiation of photons and impart to it of angular momentum, which one for the electron remains constant and equal . Electron-binding energy (see chapter 13):

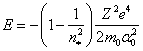                                                                (13.5.8),

where n_* - integer quantum number, which one differs from a quantum number n of the official theory of atom.

From (13.5.8) it is visible, what the energy levels are inspissated near to orbit of the Bohr and at n_*, EE₀ = 13.6 eV for hydrogen. At n_* = 1 electron is on parabolic orbit (Lyman orbit for hydrogen). The it is more n_*, the closer form of electron orbit to a circumference and the exited state is more stable, on a circular orbit of the Bohr the radiation completely misses, therefore this condition is absolutely stable. At the same time, the slightest effect on atom results in its excitation and transition of an electron to levels with large value n_*. That the atom beamed from levels of high values n_*, the very low ambient temperature and absence of extraneous particles is necessary, which one excite atom. In this regard atoms with electronic orbits near to a ground state are similar on rydberg atoms. They also can beam within the range long-wave because of a minor difference in energy of low levels, but thus to be ionized from additional small effect can not because of strong connection with a nucleus. Conditionally we shall call such atoms «cold».

From (13.5.7) and (13.5.8) it is easy to find connection between quantum numbers n and n_*:

                                                                 (13.5.9).

At n_* = 1, n = . At n_* = , n = 1.

Though the energy levels of official physics and new physics stands on attitude to each other «upward by legs», but the differences of energies between two any levels with identical values n and n_* are peer among themselves, of what it is possible to be convinced from (13.5.9).

As a result of these reasons there is a problem: when we receive from space radiation of atoms in a radio-frequency range, what atoms dispatch it? Rydberg or «cold»? I am seduced for the benefit of «cold» and I consider, that rydberg atoms can be created only in special laboratory conditions. For the benefit of «cold» atoms it is possible to result following arguments.

A. When the positive proton captures an electron, there is a radiation spectrum, in which one it is possible to watch all known spectral serials, including in the region of long waves. Radiation spectrum generated by rydberg atoms is impossible since the circular orbits are impossible (there is no place to take energy for supply of photons by angular momentum).

B. Each spectral serial has a limit of a serial. This limit from the point of view of official physics corresponds to an ionization energy of atom (n®¥), though except for a limit of Lyman serial all remaining lie in the area of energies far from an atomic ionization.

C. The transition of an electron in rydberg atoms is possible only between adjacent levels, for more distant transitions the multiple photon absorption or radiation is necessary.

D. Electron-binding energy in rydberg atoms so is small, that any photon of relict radiation (density which one very large) is capable to ionize atom. Therefore in a cloud of ionized atoms can be watched only single neutral (rydberg) atoms.

E. That was received rydberg atom the smoothly varying reduction of frequency of irradiation of atom is necessary, that this frequency was all time pursuant to frequency of photons, which one is capable to occlude atom on sequentially up energy levels. In space conditions such process is improbable.

Apparently, that for «cold» atoms of listed problems does not arise.

On a figure 13.5.1 both systems of atomic energy levels for hydrogen are figured. At the left - official scheme, on the right levels scheme of new physics. In certain conditions of occluding and radiation of energy by atom correctly to image a situation there will be this or that scheme. For example, at acquisition by a positive proton of a mobile electron the radiation spectrum will correspond to the right scheme, and at multiquantum occluding with series transition of an electron to more high-altitude orbits, the radiation spectrum at transition of an electron in a ground state will correspond to the official scheme.